Conception et ajustement de la fonction de travail du graphène via la taille, la modification, les défauts et le dopage :une étude théorique du premier principe

Contexte

En tant que matériau possédant une variété d'excellentes performances, le graphène [1,2,3] a été largement utilisé dans différents domaines, tels que les capteurs, les transistors à effet de champ (FET), les électrodes de dispositifs photovoltaïques, les diodes Schottky, les tubes à vide, et la jonction métal-semiconducteur des diodes électroluminescentes, et est devenu un substitut à de nombreux matériaux [4,5,6,7]. Les graphènes permettent de résoudre les problèmes de miniaturisation des FET et le coût des dispositifs photovoltaïques tout en conservant une bonne stabilité et de bonnes performances électriques. Cependant, la fonction de travail du graphène (WF) a une influence cruciale sur les performances de ces appareils électroniques. Par conséquent, connaître et contrôler le WF des graphènes est d'une grande importance pour les appareils électroniques à base de graphène. Généralement, les performances des dispositifs FET peuvent être déterminées par le WF des électrodes source/drain [8,9,10]. Avec les différences de WF des matériaux après le contact métal-semi-conducteur, une différence de potentiel existera dans l'interface, qui a un effet direct sur le contact Schottky ou ohmique [10]. Étant donné que l'alignement des bandes de deux matériaux différents est déterminé par leurs WF respectifs, le contrôle du WF du graphène est la clé pour réduire les barrières de contact [11].

Le graphène WF mesuré expérimentalement est d'environ 4,2 à 4,8 eV [12, 13]. Le changement de niveau de Fermi entraînera le changement de WF. De nombreuses expériences et analyses théoriques ont montré que le niveau de Fermi des graphènes peut être ajusté par dopage délibéré par des molécules aromatiques et gazeuses [14, 15] ou irradiation ultraviolette [16], fonctionnalisation de surface [17, 18], défauts [19] et électrostatique porte [20]. Par exemple, Yuan et al. ont trouvé que les WF du graphène changent considérablement via l'adsorption de Na et Cl [21]. Zhang et al. ont montré que le WF peut être finement ajusté dans la plage de 4,0 à 4,5 eV en recouvrant le graphène de cations de métaux alcalins [22]. Leenaerts et al. appris les caractéristiques intrinsèques du graphène. Les résultats ont montré que le WF du graphène à quelques couches était presque indépendant du nombre de couches, mais il peut être modulé par la couche dipolaire [23]. Volodine et al. et Peng et al. ont utilisé la méthode mécanique pour changer le graphène WF [24]. Tous ont trouvé que le WF augmenterait avec la contrainte. Yu et al. utilisé des effets de champ électrique pour ajuster le WF du graphène et a démontré que le WF peut être réglé dans la plage de 4,5 à 4,8 eV pour les graphènes monocouches et de 4,65 à 4,75 eV pour les graphènes bicouches dans des conditions ambiantes et d'azote sec [25]. Shi et al. ont constaté que le potentiel de surface des films de graphène peut être ajusté en contrôlant le temps d'immersion. Pour un temps de dopage inférieur à 20 s, le potentiel de surface a été augmenté de manière monotone jusqu'à environ 0,5 V [13]. De plus, l'irradiation s'est avérée être une méthode efficace pour contrôler la concentration de dopage. Stratakis et al. contrôlé les niveaux de dopage et de réaction pour adapter le WF des couches GO-Cl de 4,9 eV à une valeur maximale de 5,23 eV en ajustant le temps d'exposition au laser [26]. Cependant, Kang et al. réglé le WF de l'oxyde de graphène via la fonctionnalisation directe de la surface [27].

Bien que de nombreuses études antérieures aient rapporté des méthodes pour contrôler le graphène WF, les résultats de la recherche ne sont pas assez complets. Par exemple, l'étude comparative sur l'effet de taille de différents graphènes chiraux sur WF ne fournit pas d'informations suffisantes. De plus, les effets des modifications et des défauts du graphène sur WF ne sont toujours pas très clairs. Bien que l'effet du dopage sur le graphène WF ait été étudié, l'énergie de formation correspondante des atomes dopants n'a pas été mentionnée. Par exemple, dans l'expérience de Shi, le graphène a été immergé dans un AuCl₃ solution pour ajuster le WF [13]; cependant, la relation entre le WF et la concentration de dopage n'était toujours pas claire. De plus, il faut noter que les impacts des positions des groupes fonctionnels et des défauts sur le graphène WF n'ont pas encore été rapportés. Compte tenu du coût élevé des méthodes de contrôle de WF, les caractéristiques intrinsèques des différentes méthodes doivent être étudiées.

Dans cet article, une étude complète sur les méthodes de contrôle du WF a été étudiée via la théorie du premier principe. Les effets du dopage et les positions des hydroxyles et des défauts ont d'abord été rapportés et mis en évidence. Tout d'abord, des graphènes avec une chiralité différente (zigzag et fauteuil) ont été considérés, et la dépendance de WF sur la largeur du graphène a été étudiée. Deuxièmement, les WF du graphène avec des modifications de surface et des défauts ont été calculés. Différentes distributions d'hydroxyles ont d'abord été comparées, suivies de l'effet des défauts à diverses positions. Troisièmement, B, N, Al, Si et P ont été choisis comme éléments dopants pour étudier l'effet dopant des WF.

Méthodes

Tous les calculs ont été effectués dans le code CASTEP basé sur la théorie de la fonctionnelle de la densité (DFT) [28], qui est une sorte de recherche en mécanique quantique pour la structure électronique du système multi-électronique. La DFT a été largement utilisée dans l'étude des propriétés physiques et chimiques, y compris les nanomatériaux de graphènes et les nanotubes de carbone [29, 30]. La DFT peut également simuler avec précision des dizaines à des centaines de systèmes atomiques et décrire l'atome comme des particules quantiques, à savoir l'ensemble des noyaux et des électrons [31].

L'approximation de gradient généralisé (GGA) et l'approximation de densité locale (LDA) sont les fonctions d'échange-corrélation couramment utilisées dans les calculs de mécanique quantique. Ils sont décrits dans les Éqs. (1) et (2) :

où R Je et r sont respectivement les coordonnées du noyau atomique et de l'électron. L'énergie d'échange-corrélation dans le gaz d'électrons non homogène est remplacée par le E _xc [ρ ] dans un gaz d'électrons uniforme. GGA et LDA ont été utilisés pour les calculs dans les matériaux bidimensionnels. Lebègue et al. ont trouvé que la structure de bande des matériaux bidimensionnels obtenus à l'aide de LDA ou de GGA est très similaire [32]. Dans le même temps, GGA a été utilisé dans le calcul des propriétés électriques du graphène dans les recherches de Kharche et Gui, ce qui garantit la précision [33, 34].

En ce qui concerne le WF, les précédentes études basées sur des sondes à balayage avaient montré que le WF est mesuré à 4,6 eV, comme avec le graphite [35]. En règle générale, les WF compris entre 4,6 et 4,9 eV sont acceptables [36, 37]. De plus, le WF a été prédit par LDA [38] et GGA [39] à 4,48 et 4,49 eV, respectivement. En comparaison avec la date de l'expérience, le WF calculé par la théorie est légèrement plus petit. GGA a rejoint un gradient de densité non local et sa non-localité est plus appropriée pour traiter l'inhomogénéité de densité, mais LDA fonctionne mieux dans un système d'empilement. Par conséquent, dans les calculs de WF et de propriété électrique du graphène, GGA a été choisi dans cette étude théorique. De plus, dans ce calcul, la distance du vide est fixée à 15 Å de sorte que les interactions électrostatiques entre les deux côtés d'une dalle sont négligeables et que le potentiel électrostatique atteint sa valeur asymptotique. Le pseudopotentiel ultradoux est utilisé pour décrire l'interaction entre les électrons et les ions. L'énergie de coupure est à 340 eV, la zone de Brillouin est échantillonnée à l'aide d'une grille à points k de 9 × 9 × 1 de Monkhorst–Pack [40], et le frottis de Methfessel–Paxton [41] est à 0,05 eV. Le critère de convergence de l'énergie de champ auto-cohérent était de 1,0 × 10 ⁻⁶ eV, et la force MAX est de 0,03 eV/Å.

Résultats et discussion

WF de graphènes en zigzag et fauteuil avec différentes tailles

De manière générale, WF peut être défini comme l'énergie minimale nécessaire pour extraire un électron du volume à l'infini [42]. Comme dans les calculs de mécanique quantique, WF est défini comme la différence entre le niveau de vide (V ₀ ) et le niveau de Fermi (E _f ), comme le montre l'éq. (3) :

Les calculs CASTEP pour les surfaces cristallines sont effectués sur des dalles avec une zone de vide. En effet, une gamme infinie de plaques de matériau périodiques 2D est séparée par de larges espacements sous vide. CASTEP produit l'énergie de Fermi pour de tels systèmes et la distribution spatiale du potentiel électrostatique [43]. Le graphène avec différentes largeurs a diverses propriétés. Les modèles avec différentes chiralité de zigzag et de fauteuil ont été choisis pour élucider l'effet de la largeur sur le WF. Dans ce calcul, des échantillons avec la plage de cellules de une à sept unités ont été calculés. La figure 1 illustre la définition de la taille des graphènes en zigzag et en fauteuil. L'orientation cristalline des graphènes en zigzag et en fauteuil est différente; la structure cristalline du graphène en zigzag est rhombique mais la structure cristalline du graphène en fauteuil est dimétrique, comme le montre la Fig. 1a, b. La largeur du graphène est définie dans le sens horizontal et la longueur du graphène est définie dans le sens vertical. De plus, une cellule unitaire est définie comme un anneau de carbone.

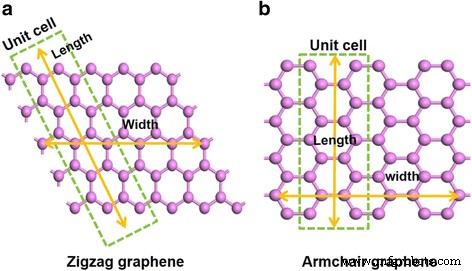
La définition de la taille du graphène. Les structures schématiques de zigzag (a ) et fauteuil (b ) graphènes qui illustrent la définition de la taille du graphène. Une cellule unitaire est définie comme un anneau de carbone dans la boîte verte. Les flèches jaunes représentent le sens de la largeur et de la longueur

La bande interdite du graphène change avec le changement de la largeur du graphène. De manière générale, le graphène en zigzag présente une propriété métallique et le graphène en fauteuil présente une propriété semi-métallique. Cependant, quelle est la relation entre WF et largeur dans les graphènes ? La figure 2 montre la relation entre la taille du graphène et le WF. La longueur et la largeur des graphènes sont inégales sur la Fig. 2a dans laquelle la longueur est constamment définie comme des cellules de sept unités mais la largeur est arrangée d'une unité à sept cellules (1 × 7 à 7 × 7), tandis que le la longueur et la largeur sont égales sur la figure 2b dans laquelle la taille est disposée de 2 × 2 supercellules à 7 × 7 supercellules. Le WF est grandement affecté par la largeur du graphène. Généralement, avec l'augmentation de la taille du graphène, le WF diminue. De plus, le WF des graphènes en zigzag est toujours plus grand que celui des graphènes en fauteuil. Nous suggérons que ce phénomène est causé par la structure cristalline du graphène. En fait, l'orientation des cristaux a un impact important sur les performances des matériaux. La structure cristalline du graphène en zigzag est une structure cubique, tandis que la structure cristalline du graphène fauteuil est une structure en diamant. En comparant le WF entre les Fig. 2a, b, le WF des graphènes (le graphène de la Fig. 2a) avec la largeur et la longueur inégales serait plus grand que celui du graphène (le graphène dans la Fig. 2b) avec la même largeur et la longueur. Le gradient de réduction du WF sur la figure 1a est également plus important. De plus, la différence de WF entre les supercellules 6 × 6 et 7 × 7 dans les graphènes fauteuil et zigzag est faible; nous pensons que le WF sera stable lorsque la taille du graphène atteint les supercellules 6 × 6.

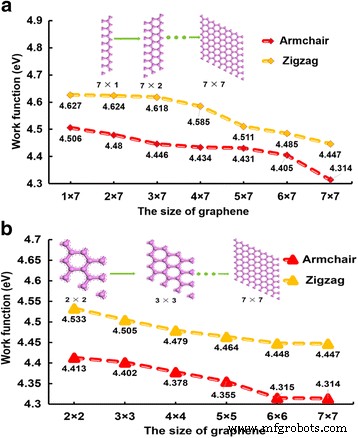
La relation entre la taille du graphène et WF. La relation entre la taille du graphène et WF. La longueur et la largeur des graphènes sont différentes dans (a ), alors qu'il en est de même dans (b )

Les bandes interdites des graphènes de différentes largeurs ont également été analysées, comme indiqué dans le tableau 1. En général, les graphènes de petite taille auront une petite bande interdite. Cependant, à mesure que la largeur augmente, la bande interdite diminue ou même se ferme [44]. Fils et al. ont montré que les nanorubans de graphène avec des bords homogènes en forme de fauteuil ou de zigzag ont tous des écarts énergétiques qui diminuent à mesure que la largeur du système augmente [45]. Le tableau 1 montre également que la bande interdite diminue avec la taille du graphène. Dans l'ensemble, la bande interdite des graphènes en fauteuil est plus petite que celle des graphènes en zigzag. Les graphènes de largeur et de longueur inégales possèdent également une bande interdite plus importante que les graphènes de largeur et de longueur égales.

Effets des hydroxyles, défauts et positions des hydroxyles et défauts sur le WF

La fonctionnalisation est toujours considérée comme une méthode de modification dans la conception et l'amélioration des performances du matériau cible; l'hydroxylation est l'une de ces méthodes. L'influence de la quantité et de la position des hydroxyles et des défauts sur le WF est analysée, comme le montre la figure 3. Les encarts (a) et (b) illustrent les diagrammes de structure des positions des hydroxyles et des défauts dans le graphène, respectivement. Dans ce calcul, des graphènes en zigzag vierges avec une taille de supercellule 4  ×  4 sont sélectionnés et le WF calculé est de 4,479 eV, ce qui est légèrement inférieur à celui du résultat de l'expérience [12]. La modification hydroxyle entraînera une augmentation du WF. Kang et al. déterminé que la valeur WF de l'oxyde de graphène par l'expérience était de 4,91 eV [27]. Cependant, le nombre de groupes fonctionnels et leurs positions n'ont pas été signalés. Le WF des graphènes en zigzag avec un hydroxyle que nous avons calculé est de 4,504 eV, ce qui est plus grand que celui des graphènes en zigzag vierges. Parallèlement à l'augmentation des hydroxyles, le WF augmente. De plus, l'incrément est relativement important; le WF maximum atteint 5.102 eV. Ce résultat est dû à l'effet hydroxyle, qui est mis en évidence avec l'augmentation du nombre des hydroxyles. De plus, quatre hydroxyles sont choisis pour analyser l'effet de la distribution des groupes fonctionnels sur le WF. L'encadré (a) donne quatre manières différentes de distribuer les hydroxyles ; les distributions sont symétriques. Avec une distribution intensive, le WF est grand. Cependant, avec une distribution dispersée, le WF est petit. La valeur maximale de WF est de 4,829 eV, tandis que la valeur minimale de WF est de 4,658 eV. Ce phénomène devrait être causé par l'effet d'agrégation des hydroxyles. En outre, quatre sites de défauts différents dans le graphène 4 × 4 sont étudiés, comme indiqué dans l'encadré (b). En général, les défauts se traduiront par la diminution du graphène WF. Bae et al. ont montré que le graphène WF était plus petit lorsque la vacance existait. Et plus le taux de défauts était petit, plus le WF devenait petit [46]. Le WF du graphène avec le défaut au centre est de 4,337 eV, tandis que le WF du graphène avec le défaut dévié du centre est plus grand à 4,363 eV, ce qui est légèrement inférieur à celui du graphène en zigzag vierge 4 × 4. Cette différence signifie que les défauts au centre ont plus d'impact sur la structure, donc le WF est à son plus petit. Par conséquent, nous suggérons que les sites de défauts centraux ont un effet important sur le WF, tandis que les défauts déviés du centre ont un effet plus faible. Kim et al. ont constaté que le dopage des trous entraîne une différence de WF pouvant atteindre 400 meV, ce qui est cohérent avec ce que nous calculons [47].

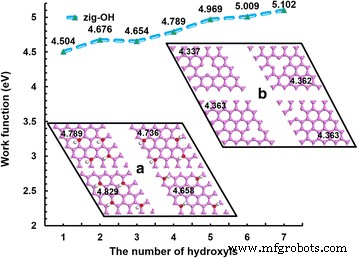
La relation entre le WF et le nombre d'hydroxyles. La relation entre le WF et le nombre d'hydroxyles ; la taille du graphène est fixée à 4 × 4 supercellules. Les images en médaillon présentent quatre modes de distribution différents des hydroxyles (a ) et les défauts (b )

Effet des dopants de B, N, Al, Si et P sur le WF

Le dopage est un moyen efficace de contrôler le WF, la bande interdite et les propriétés d'adsorption. Ainsi, les effets de dopage et les concentrations sont étudiés dans cette étude. La figure 4 montre l'effet de différents dopants sur le WF ; la taille du graphène est de 4 × 4 supercellules. Les dopants de 1, 2, 3, 4, 5 et 6 atomes répondent aux concentrations à 2,4, 4,9, 7,3, 9,8, 12,2 et 14,6 %, respectivement. L'effet des dopants sur le WF est important et suit une certaine tendance. Premièrement, le WF de tous les graphènes dopés diminue à mesure que la concentration augmente, à l'exception du graphène dopé B, qui affiche un effet opposé. Legesse et al. ont également trouvé que le WF du graphène dopé aux métaux alcalins diminue avec l'augmentation de la concentration [48]. Deuxièmement, l'incrément du WF dans le graphène dopé B et Al est relativement plus important que celui des autres graphènes. En comparant la valeur WF, les graphènes de type p dopés avec B et Al ont un WF plus grand, et la valeur maximale est jusqu'à 5,148 eV pour le graphène dopé B à une concentration de 14,6%. En revanche, le WF est beaucoup plus petit dans les graphènes de type n dopés avec N et P; la valeur minimale est diminuée à 3,23 eV à une concentration de 14,6 % dans du graphène dopé au P. Kwon et al. ont également montré que les dopants p augmenteraient le WF du graphène de 4,2 à 5,14 eV [49]. Kvashnin et al. ont également démontré le phénomène selon lequel le dopage B entraînerait une augmentation de WF, mais le dopage N et P a entraîné une diminution de WF [19, 50]. De plus, le WF des graphènes dopés Si est relativement stable. Cela peut être dû au fait que les atomes C et Si sont des congénères. Par conséquent, nous suggérons que le dopage de type p conduirait à une augmentation de WF; cependant, le montant est déterminé par les éléments dopants. Le WF a tendance à être stable à la concentration de 14,6%. D'un autre côté, le dopage de type n entraînera une forte diminution du WF.

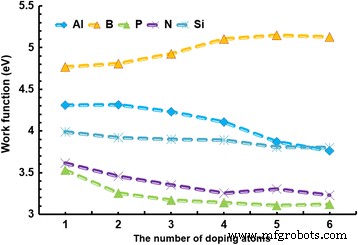
La relation entre le WF et le nombre d'atomes dopants. La relation entre le WF et le nombre d'atomes dopants. Différents types de dopants, par exemple Al, B, P, N et Si, sont dopés dans le graphène avec la taille de 4 × 4 cellules

Bien que l'influence des dopants sur le WF ait été analysée et ait une importance vitale pour l'application du graphène, la faisabilité du dopage pour divers atomes est différente. Ainsi, nous calculons l'énergie de formation de différents atomes dopants dans les GNR. L'énergie de formation [51] est décrite comme Eq. (4) :

où E _formation est l'énergie de formation, E _(GNR) est l'énergie des GNR vierges, E _{(GNR + d )} est l'énergie des GNR dopés, d est l'atome dopant, n est le nombre, et E _C et E _d sont les potentiels chimiques déterminés pour les atomes de carbone et de dopage.

L'énergie de formation peut être utilisée pour évaluer si la faisabilité de l'utilisation d'atomes pour le dopage est bonne ou non. Plus l'énergie de formation est petite, plus le dopage devient facile. La figure 5 montre que le graphène dopé avec Al a l'énergie de formation la plus grande mais la plus instable ; l'augmentation des atomes d'Al conduit à des changements spectaculaires de la structure du graphène avec une taille de cellule de 4 × 4. En revanche, l'énergie de formation de B et N est très faible, mais de petits changements sont évidents avec l'augmentation du nombre d'atomes. Les atomes d'Al, Si et P ont plus de fluctuations dans l'énergie de formation par rapport aux atomes de B et N. C'est parce que les énergies de formation d'Al, Si et P dans le graphène sont grandes, ce qui signifie que l'Al-, Si - et les graphènes dopés P sont moins stables, en particulier le graphène dopé Al a la structure la plus instable. Ils sont relativement difficiles à doper en graphène. Globalement, le dopage Al dans le graphène est difficile, tandis que le dopage B et N est plus facile. Le WF et l'énergie de formation de ces dopants dans le graphène sont enregistrés dans le tableau 2.

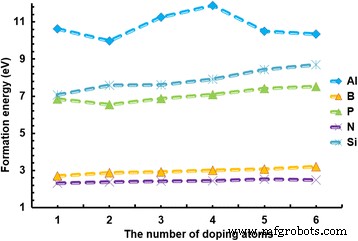
La relation entre l'énergie de formation et le nombre d'atomes dopants. La relation entre l'énergie de formation et le nombre d'atomes dopants. Différents types d'atomes dopants, par exemple Al, B, P, N et Si, sont dopés dans le graphène avec des tailles de cellules de 4 × 4

Conclusions

Le WF du graphène dans différents états, tels que la modification de surface, le dopage et les défauts, sont étudiés dans cette étude. Fondamentalement, le WF diminue à mesure que la largeur du graphène augmente. Pour la modification hydroxyle, le WF est grand lorsque le nombre d'hydroxyles augmente. De plus, lorsque la distribution des hydroxyles est intensive, le WF est également augmenté. Le défaut diminuerait le graphène WF, qui ne dépend pas des positions. Le dopage de type p avec B et Al conduirait le WF à augmenter; cependant, la quantité augmentée est déterminée par les dopants. Le dopage de type n avec N et P réduit considérablement WF. Ces découvertes fourniront un support théorique pour contrôler le graphène et améliorer encore la conception d'appareils à base de graphène.