Évolution morphologique des substrats Si(001) à motifs de fosse entraînée par la réduction de l'énergie de surface

Contexte

L'hétéroépitaxie mésappariée sur le réseau de plusieurs semi-conducteurs (tels que Ge/Si ou InGaAs/GaAs) peut conduire à la formation d'îlots 3D, suivant le mode de croissance de Stranski-Krastanow (SK). Alors que la possibilité d'obtenir de tels points par auto-assemblage pur [1, 2] est particulièrement attrayante et a suscité un intérêt généralisé, on s'est vite rendu compte que la nucléation aléatoire pouvait gravement entraver les applications, ainsi que la dispersion de la taille et de la forme.

Des décennies de recherche ont conduit au développement d'une grande variété de méthodes pour conduire la croissance hétéroépitaxiale vers la formation de structures ordonnées [3-7]. Parmi eux, il a été démontré que l'utilisation de substrats à motifs de fosses est l'une des méthodes les plus polyvalentes afin d'obtenir à la fois un ordre élevé et un contrôle de la taille des îlots hétéroépitaxiaux [8-15].

Les substrats à motifs de fosses sont généralement fabriqués au moyen de méthodes telles que la lithographie par nanoimpression [16–18], la lithographie par faisceau électronique [13, 14] combinée à la gravure ionique réactive (RIE) [19, 20] ou à la gravure chimique humide [21, 22], et la nanoindentation [23, 24], c'est-à-dire par des approches descendantes. Avec ces méthodes, les modèles ordonnés de fosses sont conçus avec une grande précision et, dans des conditions de croissance appropriées [14, 25], conduisent à un ordre latéral presque parfait.

Comme la forme réelle des creux influence l'énergie du système et, plus généralement, la nucléation des îlots [26, 27], il est crucial de contrôler leur morphologie. Ce n'est pas anodin :après tout, les fosses ne sont que des trous percés dans le substrat. Ainsi, à des températures suffisamment élevées, la capillarité [28] devrait produire une évolution morphologique, conduisant finalement à une guérison complète. En fait, des processus de recuit ou un dépôt supplémentaire du matériau du substrat après la formation initiale de la piqûre sont souvent utilisés afin d'obtenir des formes métastables reproductibles et à longue durée de vie [8, 26]. Notez que même une fois qu'une fosse est stabilisée en forme, une évolution ultérieure peut être entraînée au cours de l'hétéroépitaxie réelle [29, 30].

Dans ce travail, nous visons à décrire l'évolution des substrats à motifs de fosses entraînés par la réduction de l'énergie de surface via la diffusion de surface. Nous adoptons une approche de champ de phase appropriée [31], permettant la simulation d'échelles de longueur et de temps compatibles avec celles expérimentales [32]. Le modèle a déjà été adopté pour tenir compte de la cinétique de diffusion limitée au cours de l'évolution morphologique dans les systèmes hétéroépitaxiaux [33-36]. De plus, il a été démontré qu'il décrit correctement l'évolution vers l'équilibre, y compris les énergies de surface anisotropes réalistes [37-39].

Sans perdre en généralité, nous nous concentrerons sur les cas pertinents de surfaces Si(001) à motifs de fosses, largement étudiés dans la littérature [8, 10, 14, 30, 40, 41].

Le travail est organisé comme suit. Dans la section « Modèle de champ de phase », nous illustrons brièvement le modèle de champ de phase utilisé pour décrire l'évolution par diffusion de surface incluant l'énergie de surface anisotrope. De plus, nous décrivons comment la forme réelle de Si Wulff est prise en compte dans l'approche considérée. Dans la section « Lissage des fosses de Si(001) », le lissage attendu des fosses de Si(001), entraîné par la réduction de l'énergie de surface, est discuté en considérant différentes configurations initiales, décrivant la voie cinétique vers l'équilibre. Dans la section « Imiter le changement de forme dû à la surcroissance de Ge », une application de la méthode à un cas spécifique de croissance hétéroépitaxiale qui correspond au changement de forme induit par l'énergie de surface lors du dépôt d'une couche mince de Ge sur une fosse de Si est envisagée. Les conclusions et remarques sont résumées dans la section « Conclusions ».

Méthodes

Modèle Phase-Champ

Le modèle de champ de phase considère un paramètre d'ordre continu φ , variant entre φ =1 (solide) et φ =0 (vide) [31, 32]. L'approche est basée sur une fonctionnelle énergétique [37],

avec \(\Omega \in \mathbb {R}^{3}\) le domaine de définition de φ (r ) et r =(x ,y ,z ). Le premier terme correspond à l'énergie d'interface entre les phases dans le domaine d'interface diffuse défini par φ , c'est-à-dire à l'énergie de surface de la phase solide. \(\gamma (\hat {\mathbf {n}})\) est la densité d'énergie de surface, avec \(\hat {\mathbf {n}}\) la normale à la surface pointant vers l'extérieur, et ε l'épaisseur de l'interface entre les phases. B (φ )=18φ ² (1−φ ) ² est un potentiel de double puits avec un minimum en φ =0 et φ =1 comme dans Réf. [31]. Le deuxième terme de l'équation. (1) est la régularisation de Willmore qui est requise dans le régime d'anisotropie forte pour éviter la formation d'angles aigus [37, 38, 42]. β est un paramètre correspondant à l'arrondi du coin.

L'évolution pour φ reproduit la cinétique de diffusion limitée des surfaces et est donnée par le modèle dégénéré de Cahn-Hilliard, c'est-à-dire

où μ =δ F /δ φ est le potentiel chimique, D est le coefficient de diffusion, et M (φ )=(36/ε )φ ² (1−φ ) ² est la fonction de mobilité restreinte à la surface. L'équation pour μ lit

avec κ =−ε ∇ ² φ +(1/ε )B ^′ (φ ) et g (φ )=30φ ² (1−φ ) ² [33, 37, 38]. Cette dernière est une fonction stabilisatrice qui assure une convergence de second ordre dans l'épaisseur de l'interface, sans affecter la description du transport de matière via la diffusion de surface [43, 44]. Le profil dans la direction perpendiculaire à l'interface à l'équilibre est bien décrit par

où d (r ) est la distance signée au centre de l'interface entre les phases. Cette équation est adoptée pour définir la condition initiale pour φ comme spécifié dans ce qui suit. Nous appelons la surface de la phase solide le φ 0,5 isosurface. Toutes les propriétés géométriques de la surface considérée peuvent être déduites de φ , comme la normale de surface pointant vers l'extérieur \(\hat {\mathbf {n}}=- \nabla \varphi / | \nabla \varphi |\).

Énergie de surface anisotrope

Afin de décrire les énergies de surface anisotropes, nous avons considéré la définition de la densité d'énergie de surface, \(\gamma (\hat {\mathbf {n}})\), telle qu'introduite dans [38, 39] :

où les orientations préférentielles \(\hat {\mathbf {m}}_{i}\), c'est-à-dire les directions le long desquelles la densité d'énergie de surface a un minimum, peuvent être fixées arbitrairement avec leurs profondeurs relatives, _i , en ce qui concerne γ ₀ . Les paramètres w _i contrôler l'extension des régions où \(\gamma (\hat {\mathbf {n}})<\gamma _{0}\) autour de m _i directions, c'est-à-dire qu'il s'agit des largeurs des minima (voir aussi Réf. [38]).

Pour tenir compte de l'anisotropie spécifique des cristaux de Si, nous définissons les directions d'énergie minimales, m _i , correspondant à 〈001〉, 〈113〉, 〈110〉 et 〈111〉 [45]. α _i les coefficients, déterminant la profondeur des minima, sont obtenus par [39]

où α _〈001〉 =0.15 est défini comme référence et les différents γ _i correspondent aux valeurs d'énergie de surface des orientations susmentionnées telles que rapportées dans la réf. [45]. Sans perte de généralité, on pose γ ₀ =1. En effet, les rapports des minima et de la force de l'anisotropie peuvent être contrôlés par le α _i valeurs de l'éq. (6) et α _〈001〉 , tandis que γ ₀ joue le rôle d'un préfacteur dans l'équation. (2), affectant ainsi uniquement l'échelle de temps absolue de l'évolution.

La largeur des minima d'énergie dans l'équation. (5) sont définis sur w _i =50 pour toutes les directions minima, sauf pour w _〈113〉 =100 [39]. Selon cette définition des paramètres, les angles vifs sont prédits dans la forme de Wulff, c'est-à-dire que l'anisotropie de l'énergie de surface est « forte » [38, 42, 46]. Par conséquent, la régularisation de Willmore est strictement nécessaire pour effectuer les simulations. Le β value définit l'extension de la région arrondie aux coins, qui sont connus pour avoir un rayon proportionnel à \(\sqrt {\beta }\) [37]. Afin d'effectuer des simulations, l'échelle de longueur définie par l'arrondi au coin par β doit être supérieure à la résolution de la discrétisation spatiale de la méthode numérique. Cependant, il convient de mentionner que les petites facettes éventuellement présentes dans la forme Wulff avec une extension de l'ordre de \(\sqrt {\beta }\) peuvent être masquées lors de l'utilisation de β trop grands valeurs ainsi qu'un facettage à petite échelle impliquant des orientations préférentielles réellement présentes dans la forme de Wulff. Dans ce travail, nous définissons β =0,005. Selon la taille du domaine de simulation, précisée dans la suite, cette valeur permet d'adopter une discrétisation spatiale réalisable. De plus, toutes les orientations préférentielles entrant dans les Eqs. (5) et (6) sont reproduits. En revanche, un éventuel facettage impliquant des échelles plus petites que ∼0,07 ne peut pas être reproduit en raison de l'extension de l'arrondi des coins.

Configuration initiale de la morphologie et de la simulation

Afin d'étudier toute évolution morphologique par le modèle de champ de phase défini dans cette section, une condition initiale appropriée pour φ doit être réglé. On considère ici une géométrie de fosse lisse taillée dans une surface plane (001), avec un référentiel fixé à \(\hat {\mathbf {x}}=\,[\!100]\), \(\hat {\ mathbf {y}}=\,[\!010]\), et \(\hat {\mathbf {z}}=\,[\!001]\). En particulier, on considère une surface circulaire (001) de rayon L à une hauteur h ₀ −H , relié en douceur à la surface plane environnante (001) à la hauteur h ₀ . Une telle géométrie est définie comme condition initiale pour φ en exploitant l'Eq. (4) avec d (r ) la distance signée de la surface Γ (x ,y ) défini par

avec \(r=\sqrt {x^{2}+y^{2}}\) et

R =H /4L est défini comme un paramètre de rapport d'aspect, tandis que σ est un paramètre contrôlant l'extension de la liaison continue entre le fond de la fosse et la zone plane qui l'entoure. Ce paramètre est défini ici sur σ =L /2.

Dans la figure 1, la condition initiale adoptée pour φ est illustré. La figure 1a montre Γ (x ,0) profils avec différentes valeurs de R . La figure 1 b montre la définition de φ au moyen de l'éq. (4) dans un domaine parallélépipédique 3D. En particulier, ce panneau montre une coupe transversale passant par le centre de l'ensemble du domaine. La partie gauche montre la région correspondant à la phase solide, c'est-à-dire la région où φ>0,5, révélant la surface qui correspond à la morphologie initiale de la fosse. La partie droite illustre les valeurs de φ dans l'ensemble du domaine 3D, c'est-à-dire dans les phases de masse et dans la transition continue entre elles.

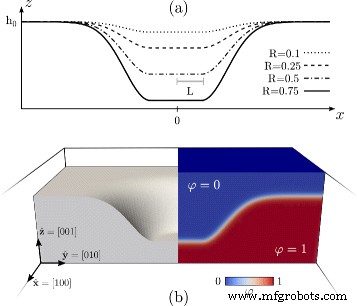
Condition initiale pour le modèle de champ de phase, ressemblant à une fosse lisse à la surface (001) d'un film solide. un Γ (x ,0) profils de l'éq. (7) obtenu pour différents R valeurs. b Définition de φ dans le domaine 3D adopté pour les simulations numériques. Il est obtenu à partir de l'éq. (4) avec d (r ) la distance signée de Γ (x ,y ) avec R =0,5. A gauche, la phase solide où φ> 0,5 s'affiche. A droite, une carte en couleur montrant φ dans le domaine 3D est signalé

Des simulations numériques sont effectuées pour intégrer les équations. (2) et (3). Ils sont réalisés en utilisant la boîte à outils de la méthode des éléments finis (FEM) AMDiS [47, 48], avec un schéma d'intégration semi-implicite et un raffinement de maillage à l'interface [33, 38, 49]. Les conditions aux limites périodiques sont définies le long des directions \(\hat {\mathbf {x}}\) et \(\hat {\mathbf {y}}\). Les conditions aux limites sans flux (Neumann) sont définies en haut et en bas du domaine de simulation le long de la direction \(\hat {\mathbf {z}}\). L'échelle de temps de l'évolution est échelonnée d'un facteur 1/D , qui correspond à l'ensemble D =1. Dans ce qui suit, nous nous référons au temps des simulations en unités arbitraires. La taille de la fosse est arbitrairement définie sur L =1, tandis que l'épaisseur de l'interface est définie sur ε =0.2.

Résultats et discussion

Lissage des fosses Si(001)

Dans cette section, nous illustrons les résultats concernant les changements morphologiques au cours de l'évolution des substrats de Si(001) à fossettes. Le modèle décrit ci-dessus permet de décrire le cas particulier du silicium au moyen de la définition de l'énergie de surface anisotrope comme dans la section « Énergie de surface anisotrope ». Nous nous attendons à ce que les résultats suivants soient valides d'un point de vue qualitatif pour n'importe quelle taille, à condition que le système soit suffisamment grand pour adopter une approche de continuum (\(\gtrsim 10\) nm) [32] et que la forme puisse être paramétrée par le rapport hauteur/largeur R similaire à la figure 1 a. L'échelle de longueur réelle peut être considérée en réglant le L paramètre à celui correspondant en unités réelles, L ^r . L'échelle en temps réel peut alors être décrite en tenant compte des valeurs réelles de D et γ ₀ et en multipliant par le L ^r longueur, c'est-à-dire par mise à l'échelle par L ^r /L avec L unitaire comme spécifié ci-dessus.

Concentrons-nous d'abord sur les premières étapes de l'évolution. La condition initiale fixée par l'Eq. (7) est constitué d'un profil qui ne présente aucune orientation préférentielle de la surface. Lorsque l'on considère l'évolution par diffusion de surface induite par la réduction d'une énergie de surface anisotrope, un facettage du profil initial est attendu. Ceci est illustré sur la Fig. 2 où le facettage de deux profils avec R =0,25 dans la Fig. 2a et R =0,5 sur la figure 2b sont indiqués. Une échelle de couleurs illustre les valeurs \(\gamma (\hat {\mathbf {n}})\) à la surface. Cela permet d'identifier les facettes comme les régions avec une densité d'énergie de surface presque uniforme correspondant aux minima de l'Eq. (5), délimité par des régions localisées avec des valeurs élevées de \(\gamma (\hat {\mathbf {n}})\). Selon le rapport hauteur/largeur initial de la fosse, différentes facettes se forment. Pour le plus petit R, la facette (001) en bas est maintenue en prenant une forme carrée. Les bords de la fosse sont délimités par quatre facettes {113} reliées par de petites facettes {110} de forme triangulaire. Selon le rapport hauteur/largeur plus grand, une plus grande surface à facettes est présente lorsque l'on considère R =0,5, permettant l'apparition d'orientations préférentielles à plus forte pente par rapport à la surface (001). En particulier, la forme initiale permet la présence de facettes {111} se formant entre deux facettes {113} proches du fond et du méplat. Entre les deux, de larges {110} facettes se forment.

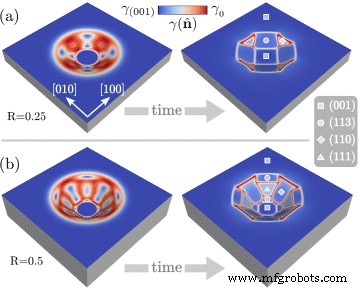
Facettage du profil initial tel que défini dans la section « Initial Morphology and Simulation Setup » en fonction de la diffusion de surface et \(\gamma (\hat {\mathbf {n}})\) reproduisant l'énergie de surface du Si. Deux morphologies initiales différentes sont considérées :a R =0,25 et b R =0,5. Sur les morphologies facettées, des symboles sont adoptés pour identifier les familles de facettes. L'échelle de couleurs montre les valeurs de \(\gamma (\hat {\mathbf {n}})\) à la surface

Les résultats rapportés sur la figure 2 montrent la possibilité de prédire la morphologie des fosses facettées selon le rapport hauteur/largeur ou, en général, selon la morphologie initiale. Nous étudions maintenant également la dynamique à longue échelle de temps inspectant l'évolution morphologique jusqu'à l'équilibre [38]. Ceci est illustré sur la figure 3 où nous nous concentrons sur la fosse la plus profonde considérée jusqu'à présent, c'est-à-dire avec R =0,5, et les principaux changements morphologiques sont indiqués. En particulier, des vues en perspective et de dessus des différentes morphologies obtenues au cours de l'évolution sont rapportées sur les Fig. 3 a, b, respectivement. Dans la première étape de cette simulation, on observe la disparition des facettes {111} les plus abruptes et l'agrandissement des facettes {113} voisines. Ensuite, ces dernières fusionnent et le rétrécissement de {110} facettes commence. Ceux-ci disparaissent à des stades ultérieurs après avoir pris une forme triangulaire, donnant un contour carré à la fosse d'une vue de dessus. De plus, les facettes {113} finissent par disparaître et un aplatissement global est obtenu. L'échelle de temps réel obtenue dans cette simulation peut être estimée avec les données de la littérature. En particulier, nous pouvons considérer D déterminé par la loi d'Arrhenius avec le préfacteur et l'énergie d'activation de la réf. [50], où les fluctuations thermiques sont également prises en compte. γ ₀ est défini pour avoir \(\gamma (\hat {\mathbf {n}})\sim 8.7\) eV/nm ² quand \(\hat {\mathbf {n}}=(001)\) [51] de l'Eq. (5), c'est-à-dire γ ₀ =10.2 eV/nm ² . Les autres coefficients de diffusion de surface dépendants du matériau [28], c'est-à-dire le volume atomique et la densité à la surface, sont fixés pour reproduire le cas de Si. D'après ces valeurs, la durée prévue de l'ensemble du processus à haute température T ∼1100−1200 °C pour L ^r de dizaines de nanomètres est de l'ordre d'heures.

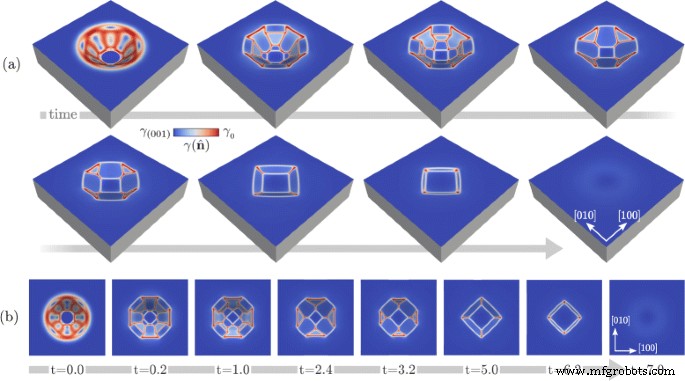
Evolution vers l'équilibre pour une fosse de Si ayant une morphologie initiale comme sur la Fig. 2b. un Vue en perspective montrant les principaux changements morphologiques. b Vue de dessus des morphologies dans le panneau a . L'heure indiquée dans le panneau b est exprimé en unités arbitraires. L'échelle de couleurs montre les valeurs de \(\gamma (\hat {\mathbf {n}})\) à la surface

Parallèlement aux changements morphologiques spécifiques survenus au cours de l'évolution, deux caractéristiques principales doivent être remarquées. Premièrement, l'évolution conduit à l'aplatissement global attendu de la surface, et cela se produit avec la disparition progressive des facettes abruptes remplacées par des facettes moins profondes. Bien que ce comportement puisse être déduit uniquement par des arguments sur la minimisation de l'énergie et l'abaissement du rapport hauteur/largeur, il convient de souligner que l'évolution complète est fournie ici, traitant de la présence de facettes similaires mais avec des tailles relatives différentes. Ceci est en accord avec le fait que les morphologies obtenues au cours de l'évolution correspondent à des configurations hors équilibre et définissent une voie vers le minimum énergétique global. Ensuite, bien que les facettes attendues et leur énergétique soient connues, la morphologie spécifique à un certain point de l'évolution ne peut être décrite qu'en tenant compte de la dynamique et pas seulement en considérant la minimisation globale de l'énergie [38].

Le deuxième point important montré par les résultats rapportés sur la figure 3 concerne les étapes intermédiaires. Lorsque la forme au cours de l'évolution se rapproche d'une géométrie avec une profondeur similaire au profil initial obtenu avec R =0,25, c'est-à-dire à t ∼3.2, la morphologie induite par la minimisation d'énergie ressemble de très près à ce qui est rapporté sur la figure 2b, même en partant d'une configuration initiale avec une différence de profondeur significative (double dans ce cas). Ceci suggère l'existence d'une voie cinétique commune vers l'aplatissement final, qui est atteint après le premier facettage rapide de la morphologie initiale. Cet argument est en fait confirmé et illustré plus en détail dans les graphiques de la figure 4. Ici, la décroissance monotone de l'énergie au cours de l'évolution après le facettage initial est rapportée lors de l'examen des fosses avec R égal à 0,1, 0,25, 0,5 et 0,75 comme dans la figure 1 a. Sur la figure 4a, l'échelle de temps exprimée en unités arbitraires est considérée. Sur la figure 4b, les mêmes changements d'énergie sont signalés avec un décalage approprié de l'échelle de temps, mettant en évidence la décroissance d'énergie similaire lorsque l'on approche des rapports d'aspect similaires de la structure. \(t^{*}_{R}\) est défini comme l'instant auquel la surface plane est obtenue, c'est-à-dire l'instant auquel le minimum global d'énergie est atteint, différent pour chaque simulation comme le montre la Fig. 4 a. Comme le montre ce graphique, les décroissances d'énergie se chevauchent presque pour R 0,5. Une très petite différence n'est observée que lorsque l'on considère R =0,75, dont les résultats de décroissance énergétique sont encore très proches des autres courbes et les différences disparaissent fondamentalement pour \(t \gtrsim 5.0\). Il convient de mentionner que pour les écarts importants par rapport à la configuration initiale, à savoir avec R ≫1, de telles géométries peuvent évoluer différemment avec des effets différents sur les échelles de temps et les morphologies [52, 53]. De plus, des changements topologiques sont connus pour se produire dans des cas extrêmes, par exemple, avec des tranchées très profondes, empêchant la possibilité d'atteindre l'équilibre global avec une surface plate (001) [34, 39, 54].

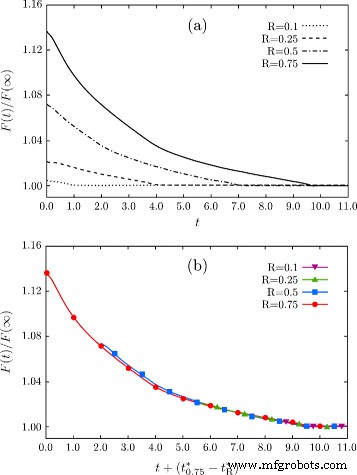
Energie décroissante au cours de l'évolution des géométries des fosses. un F (t ) normalisée par l'énergie de la surface plane (001) obtenue comme étape finale de l'évolution. Décroissances énergétiques obtenues à partir des simulations ayant différents R pour le profil initial, à savoir, de R =0,1 à R =0,75, sont affichés. Le temps est exprimé en unités arbitraires. b Courbes comme dans le panneau a décalé pour correspondre à \(t_{R}^{*}\), c'est-à-dire l'instant auquel l'aplatissement global de la fosse est réalisé en fonction de R

Les formes obtenues dans les simulations rapportées dans ces sections devraient être observées expérimentalement, en particulier lorsque le traitement implique des conditions proches de la limite thermodynamique. Certaines des morphologies rapportées sur la figure 3 correspondent en fait au contour des substrats de Si(001) à fossettes. Par exemple, une morphologie constituée d'une surface large (001) délimitée par des facettes {113} étroites comme sur la figure 3 à t ∼5,0 sont observés lors de l'examen des substrats Si(001) à motif de fosse avec un rapport d'aspect de 0,05<R <0.1 comme dans Réf. [10, 30]. De plus, l'extension relative des facettes dans l'étape susmentionnée de la simulation de la figure 3 est très similaire à ce qui a été rapporté dans ces travaux expérimentaux. Cet accord entre les simulations et les expériences évalue en outre la description théorique de la diffusion de surface adoptée ici. Cependant, nous nous sommes concentrés sur les caractéristiques générales du processus et une comparaison plus détaillée avec des expériences spécifiques est hors du but du présent travail.

Imiter le changement de forme dû à la prolifération de Ge

Comme mentionné dans l'introduction, l'une des principales applications des modèles de Si à motifs de fosses est le contrôle de la croissance d'îlots auto-assemblés [55]. Ceci est particulièrement vrai lorsque l'on considère le positionnement de Ge ou Si_{1 − c} Ge _c îlots sur substrats Si(001) [6]. Avec la méthodologie adoptée dans la section précédente, nous pouvons inspecter les changements morphologiques liés aux caractéristiques particulières de l'énergie de surface. Par conséquent, en partant d'une configuration initiale appropriée ressemblant à la morphologie réelle d'une fosse de Si et en tenant compte des différences de densité d'énergie de surface attendues lors du dépôt d'un autre matériau, nous pouvons prédire quelle est la contribution correspondante aux changements morphologiques.

L'étude de cas consiste ici en la surcroissance de Ge sur un substrat en Si(001) à fossettes avec un rapport d'aspect proche de 0,1. Le profil de la Fig. 3 à t =5,0 est considéré comme une morphologie initiale. Ensuite, une énergie de surface comprenant également un minimum le long des directions 〈105〉 est définie. Cette définition de \(\gamma (\hat {\mathbf {n}})\) imite la présence de l'orientation préférée des petites pentes dans les systèmes Ge/Si(001) [56–58]. La grande stabilité des facettes {105} est due à l'interaction entre la reconstruction de surface et les effets de déformation liés au décalage de maille entre l'épicouche et le substrat [59-61]. La valeur de densité d'énergie de surface qui doit être utilisée dans l'Eq. (6) est tiré de la Réf. [58] dans la limite d'une couche épaisse de Ge. Notez que d'autres facettes qui ont une énergie de surface plus proche du (001), telles que {1 1 10}, sont négligées ici. Comme les angles entre les directions 〈105〉 et [001] sont très petits, w _i des paramètres plus grands que ceux adoptés auparavant sont nécessaires pour décrire correctement les minima énergétiques de l'équation. (5) [38]. En particulier, nous définissons w _{105} =w _{001} =500.

Dans la figure 5, l'évolution par diffusion de surface avec la nouvelle définition de \(\gamma (\hat {\mathbf {n}})\) est rapportée. La figure 5a montre l'évolution morphologique de la surface avec un grossissement du z -axe par un facteur 5. Dans les premières étapes, des facettes {105} se forment entre les {113} facettes présentes dans le profil initial. Comme les orientations 〈105〉 ont l'énergie minimale, comme illustré également sur la figure 5b, les facettes correspondantes s'étendent tandis que les facettes {113} rétrécissent. Aux stades ultérieurs, une fosse délimitée par {105} facettes ne se forme qu'avec encore une surface (001) au fond. Vu de dessus comme sur la figure 5b, le changement de morphologie se traduit par une rotation du contour de la fosse de 45°. Ceci est en fait observé lors du dépôt de Ge sur des substrats à motifs de Si dans les expériences [41] ou lors de la croissance spontanée de piqûres dues à des défauts ou des impuretés [40]. La formation de facettes {105} s'avère également agir comme un site de nucléation préféré pour une croissance ultérieure des points Ge [30]. L'évolution illustrée sur la figure 5 démontre qu'un changement de forme conduisant à la rotation du contour de la fosse peut être obtenu en raison de la réduction de l'énergie de surface uniquement. On s'attend à ce que ce soit la situation réelle dans des conditions proches de l'équilibre, lorsque les forces motrices thermodynamiques sont dominées par les contributions de surface, c'est-à-dire pour de petits volumes de Ge. En fait, afin de décrire complètement le processus, les effets d'élasticité, le mélange et la croissance de la phase solide doivent être inclus [32]. Il convient également de mentionner que même des puits de Si moins profonds sont adoptés dans les expériences, montrant des facettes avec des normales le long de {11n } directions, avec 5<n <10 [41] (c'est-à-dire {1 1 10} facettes). La géométrie de la fosse délimitée par ces facettes conduirait à une évolution similaire, car elles correspondent à ce qui a été adopté comme configuration initiale de la figure 4 avec juste une pente plus faible par rapport au plan (001).

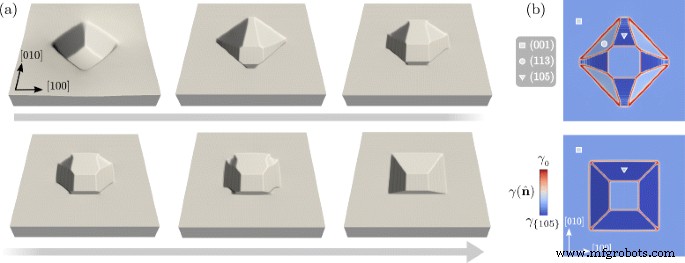
Evolution du profil de la Fig. 3 à t =5,0, avec une définition de l'énergie de surface incluant les orientations 〈105〉. un Profils de surface à des stades représentatifs de l'évolution vers la formation d'une fosse délimitée par {105} facettes seulement. z -axis est agrandi par un facteur 5. b Vue de dessus montrant les valeurs \(\gamma (\hat {\mathbf {n}})\) à la surface. La deuxième et la dernière étape du panel a sont indiqués respectivement dans la partie supérieure et inférieure. Des symboles comme dans la Fig. 2 sont adoptés pour identifier différentes familles de facettes

Conclusions

Dans ce travail, nous avons utilisé un modèle de continuum basé sur la diffusion en surface pour étudier l'évolution temporelle des fosses creusées dans un substrat de Si(001). En abordant de manière appropriée l'anisotropie de l'énergie de surface (forte), avec une paramétrisation basée sur la forme bien connue de Si Wulff, nous avons prédit des configurations métastables typiques en accord avec les expériences, y compris le cas où le dépôt d'un matériau différent introduit de nouvelles facettes stables. The entire evolution towards the global flattening of the pit has been illustrated, and it is found to follow the same kinetic pathway also when considering pits with different initial depths. We believe that the model can be predictive also for initial configurations strongly deviating from the ones which we have analyzed as examples. As a consequence, the present approach can be useful in designing experiments based on still-unexplored pit shapes. Furthermore, the model is general and can be easily adapted to different substrates upon re-parametrizing the surface energy.