Ingénierie des contraintes sur les propriétés électroniques et optiques de la bicouche WSSe

Introduction

Les matériaux bidimensionnels (2D) avec leurs nouvelles propriétés ont montré de grandes perspectives d'application dans les appareils électroniques de nouvelle génération. En tant que candidat prometteur, les dichalcogénures de métaux de transition (TMDC) à couche 2D avec bande interdite réglable ont été largement étudiés au cours de la dernière décennie et ont été intensivement exploités comme transistors à effet de champ tunnel [1], diodes électroluminescentes, photodétecteurs [2, 3], capteurs [4], et ainsi de suite.

Au-delà du MX₂ hautement symétrique (M =Mo, W; X =configuration S, Se, Te), nouveaux TMDC structurels Janus, avec la formule chimique de MXY (M =Mo, W; X ≠ Oui =S, Se, Te) ont suscité un intérêt croissant en raison de leurs propriétés optiques et électroniques distinctives. La monocouche MXY est constituée de deux couches d'atomes de chalcogène différentes marquées A, A' et d'une couche d'atomes de métal de transition B pour former un empilement atomique ABA'. Comparé à celui de MX₂ , MXY possède une configuration ordonnée par asymétrie avec la rupture de la symétrie du miroir, ce qui conduit à un dipôle vertical et à un couplage spin-orbite Rashba amélioré [5]. Les structures géométriques et électroniques de Janus WSSe ont déjà été signalées et se sont avérées avoir de nombreuses caractéristiques distinctives différentes des deux WS₂ et WSe₂ . Par exemple, l'activité catalytique de réaction de dégagement d'hydrogène du WSSe s'est avérée supérieure à celle des catalyseurs actuels à base de TMD [6]. Les transistors à effet de champ WSSe ont également obtenu de meilleures performances en mobilité électronique et I _ON /Je _OFF rapport que celui des monocouches TMD conventionnelles [7]. Malgré les caractères passionnants de la monocouche intrinsèque, les TMDC Janus avec une épaisseur de bicouche et multicouche et diverses structures d'empilement peuvent posséder de profondes connotations physiques compte tenu de l'asymétrie de la configuration MXY. Par exemple, il a été prévu que la bicouche WSSe ordonnée Se-S-Se-S améliorerait l'efficacité de la conversion photoélectrique pour les applications de cellules solaires [8].

Basé sur les matériaux Janus TMDC uniques, la réalisation d'un contrôle précis de leurs propriétés électroniques et optiques est vitale pour répondre aux multiples besoins de la conception d'appareils. Le champ électrique [9, 10], la déformation [11, 12], la décoration de surface [13, 14] et le dopage magnétique [15, 16, 17] se sont avérés efficaces pour moduler les comportements électroniques et optiques des TMDC 2D. Parmi ces méthodes, l'ingénierie des déformations est réversible avec le processus contrôlable, sans générer de défauts de réseau supplémentaires et de dommages dans les matériaux. En outre, l'ingénierie des déformations modifiera la symétrie structurelle, ce qui peut donner lieu aux caractéristiques polarisées des matériaux 2D et leur offrir de grandes perspectives dans les applications futures. Comme cela a été rapporté, le WSe₂ tendu les monocouches montrent une variation évidente dans la structure de la bande électronique [18,19,20,21,22] et démontrent des avantages uniques dans les applications des dispositifs photoactifs [23], valleytronics [18, 24], photodétecteurs [25] et matériau d'anode pour Li -batterie ionique [26]. Néanmoins, l'ingénierie des contraintes sur les propriétés électroniques et optiques, telles que l'évolution de la bande et l'anisotropie optique de la bicouche Janus WSSe 2D n'a pas encore été signalée à ce jour.

Dans ce travail, nous effectuons une enquête sur la modulation de contrainte des propriétés électroniques et optiques de la bicouche WSSe à travers les calculs de fonction de densité de premier principe. L'enquête est initiée avec la détermination de l'ordre d'empilement le plus favorable de la bicouche. Les structures de bande dépendantes de la contrainte des trois configurations stables sont calculées. Les bandes interdites des bicouches WSSe sont adaptées et la contribution orbitale atomique est révélée pour comprendre le mécanisme associé. L'anisotropie optique est également modulée en ajustant les propriétés diélectriques à travers la contrainte appliquée. Une transformation contrôlable entre les propriétés optiques anisotropes et isotropes est démontrée.

Méthode de calcul

Tous les calculs théoriques sont basés sur la théorie de la fonctionnelle de la densité (DFT) avec l'approximation du gradient généralisé (GGA). La méthode précise d'onde augmentée par projecteur (PAW), telle que mise en œuvre dans l'Ab-initio de Vienne Le code du package de simulation (VASP) [27,28,29] est utilisé. Un modèle de dalle avec une cellule unitaire 1 × 1 est construit et une couche de vide de 20 le long du z La direction est utilisée pour minimiser les interactions artificielles entre les dalles voisines. Les configurations électroniques de valence des atomes W, S et Se adoptées sont 5p ⁶ 5d ⁴ 6s ² , 2s ² 3p ⁴ , et 4s ² 4p ⁴ , respectivement. La paramétrisation GGA [30] avec Perdew-Burke-Ernzerhof (PBE) [31] est utilisée comme fonction d'échange-corrélation. Les fonctions d'onde électronique sont étendues en ondes planes avec une coupure d'énergie de 400 eV. La zone Brillouin est échantillonnée avec une grille de Monkhorst-Pack 19 × 19 × 1 de k points. La méthode de correction de dispersion DFT-D2 est incluse dans les calculs de relaxation structurelle et de structure électronique pour décrire correctement l'effet des intégrations de van der Waals. Tous les degrés de liberté atomiques, y compris les constantes de réseau, sont entièrement relâchés avec des critères de convergence auto-cohérents de 0,01 eV/Å et 10 ^-6 eV pour les forces atomiques et l'énergie totale, respectivement.

Résultats et discussion

La monocouche Janus WSSe a un réseau hexagonal, où la cellule unitaire est constituée d'un atome de W moyen dans son réseau en nid d'abeille planaire qui s'est lié de manière tridimensionnelle avec les atomes de surface S et Se. La constante de réseau optimisée de WSSe est de 3,23 avec les longueurs de liaison W-S et W-Se de 2,42 et 2,53 , respectivement, qui sont alignées sur les valeurs rapportées précédemment [32]. Selon la symétrie structurelle, cinq configurations d'empilement différentes de la bicouche WSSe sont prises en compte, qui sont respectivement marquées AA, AA', AB, AB' et A'B. Pour chaque empilement, trois ordres différents de couches de chalcogène :S-Se-S-Se, Se-S-S-Se et S-Se-Se-S sont considérés. Toutes les configurations géométriques d'équilibre de la bicouche WSSe sont représentées sur la figure 1. Chaque configuration est complètement relâchée respectivement pour optimiser l'espacement intercouche.

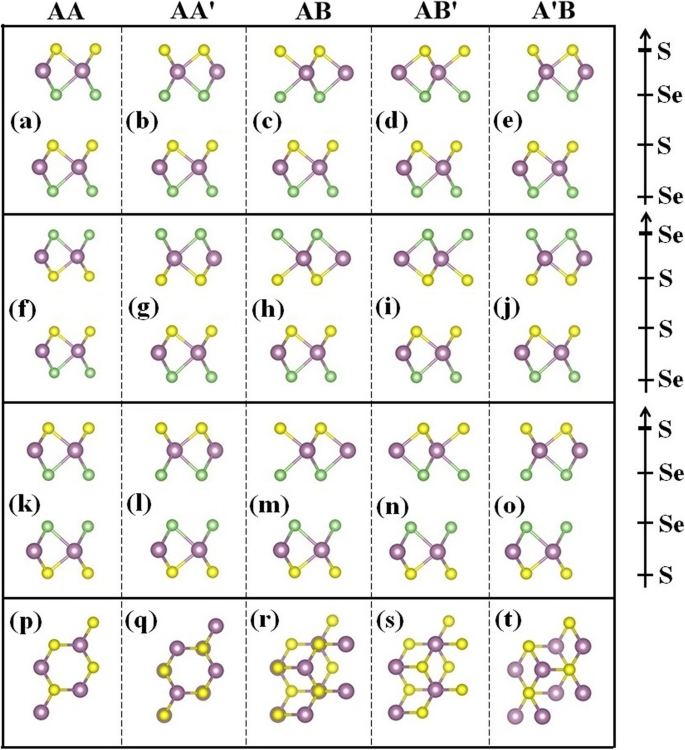
Vues de dessus et de côté de la configuration atomique de la bicouche WSSe. Les boules violettes représentent les atomes W, et les boules jaunes et vertes représentent respectivement les atomes S et Se

Afin de déterminer quantitativement la stabilité structurelle de la bicouche WSSe, les énergies de liaison E _b de toutes les configurations géométriques ci-dessus sont calculées à partir de la relation :

où E _bicouche et E _WSSe sont les énergies totales de la bicouche et de la monocouche WSSe, respectivement.

Comme le montre la figure 2, pour toutes les structures d'empilement, les couches de chalcogène avec l'ordre de S-Se-Se-S possèdent la plus grande énergie de liaison, tandis que l'ordre inversé Se-S-S-Se a la plus petite énergie de liaison. De plus, il est visualisé que AA', AA' et AB sont les configurations d'empilement les plus stables des ordres S-Se-Se-S, S-Se-S-Se et Se-SS-Se, avec les énergies de liaison de 0,322, 0,304 et 0,281 eV, respectivement. Cela indique que la bicouche Janus WSSe préfère former un empilement AA' bilatéralement symétrique avec l'ordre chalcogène S-Se-Se-S, qui est différent de l'hétérostructure MoSSe/WSSe de l'empilement AB [33].

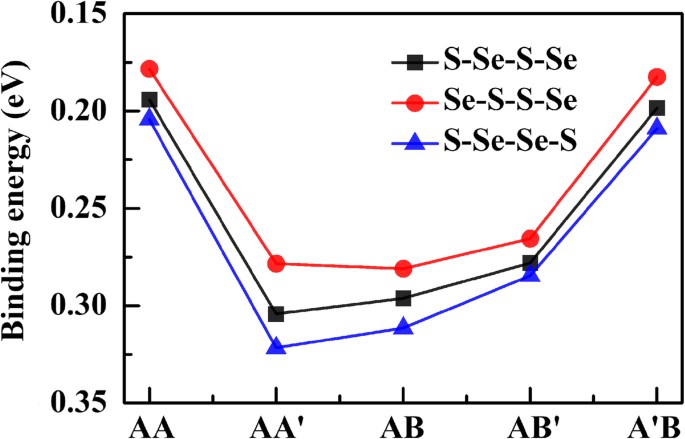
Énergies de liaison de toutes les configurations géométriques d'équilibre de la bicouche WSSe

Compte tenu des structures d'empilement les plus stables mentionnées ci-dessus pour chaque ordre de chalcogène, les propriétés électroniques et optiques sont étudiées en profondeur. Pour plus de commodité, l'empilement AA' avec structure S-Se-S-Se, l'empilement AB avec structure Se-SS-Se et l'empilement AA' avec structure S-Se-Se-S sont nommés I ₁ , Je ₂ , et Je ₃ , respectivement, dans la discussion suivante.

Structures de bande des bicouches Janus WSSe I ₁ , Je _2, et Je ₃ sont calculés, comme le montre la figure 3. Toutes les trois configurations présentent une structure de bande interdite indirecte fondamentale, qui est similaire à celle de la bicouche pure WS₂ et WSe₂ . Les maximums de bande de valence (VBM) se situent tous à Γ point, tandis que le minimum de bande de conduction (CBM) situé à K point pour Je ₁ , et situé entre K et Γ points pour les deux I ₂ et Je ₃ . La bande interdite indirecte de I ₃ est calculé comme étant d'environ 1,3 eV, légèrement supérieur à celui de I ₁ et Je ₂ dont les bandes interdites sont d'environ 1,0 eV. Malgré le fait que les bandes interdites soient sous-estimées sans la fonction hybride blindée HSE06, les distributions de structure de bande n'ont pas de changement significatif et, par conséquent, la sous-estimation n'influencera pas substantiellement la tendance à l'évolution des propriétés électroniques sous la modulation de contrainte.

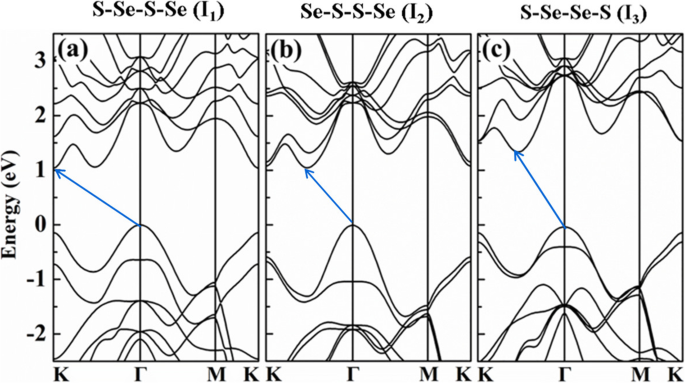
Structures de bande de I ₁ , Je ₂ , et Je ₃ , respectivement, où les bandes interdites sont indiquées par les flèches bleues

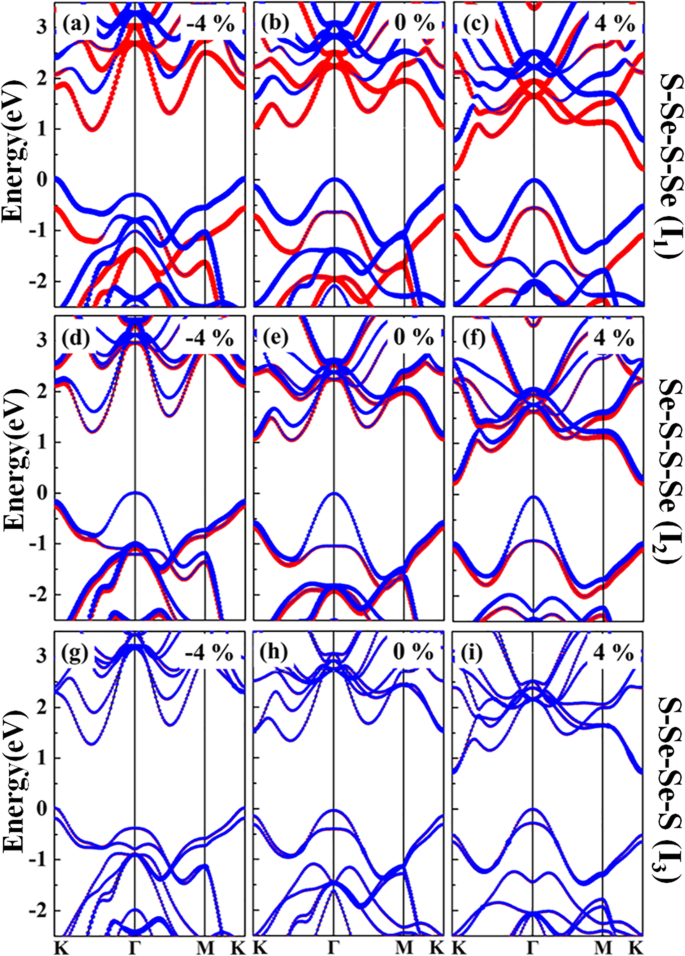
L'ingénierie des contraintes est une méthode prometteuse pour manipuler la symétrie structurelle et l'interaction entre les couches, ce qui pourrait donner lieu à de nombreux phénomènes de charme. Pour étudier les structures électroniques des bicouches WSSe modulées par la déformation appliquée, les bandes d'énergie sont analysées, comme illustré sur la figure 4a–r. Lorsqu'une contrainte de compression allant de − 6 à − 2% est appliquée, le VBM d'origine à Γ point changé en K point pour Je ₁ et Je ₃ configurations, tandis que montre peu de variété pour I ₂ . Le CBM original à K le point se déplace vers la position entre Γ et K points pour les trois structures. Une fois que la contrainte de traction dans la région de 2% ~ 6% est utilisée, le VBM reste à Γ point tandis que le CBM se situe au point K.

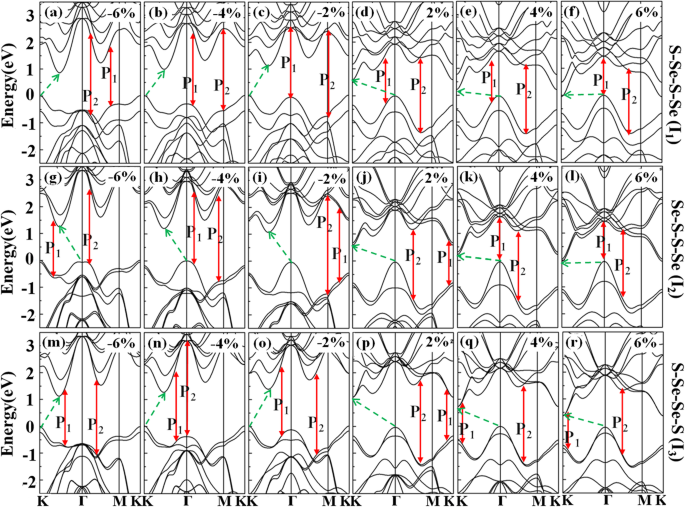
un –r Structures de bande de I ₁ , Je ₂ , et Je ₃ avec différentes souches de − 6%, − 4%, − 2%, 2%, 4% et 6%, respectivement. Les bandes interdites sont indiquées par les flèches vertes en pointillés, tandis que les flèches rouges pleines représentent les principales transitions interbandes de P ₁ et P ₂ , respectivement

La figure 5 résume la bande interdite dépendante de la contrainte pour les trois structures. Il est évident en un coup d'œil que les réponses de la bande interdite à la contrainte de compression et à la contrainte de traction sont non seulement avec une réactivité inégale, mais également avec des gradients différents à mesure que la contrainte appliquée augmente. La bande interdite est moins sensible à la contrainte de compression, tandis qu'elle diminue considérablement avec les contraintes de traction améliorées. Au fur et à mesure que la contrainte de compression augmente, le CBM des deux I ₁ et Je ₃ est élevé à une énergie plus élevée, tandis que celle de I ₂ est rétrogradé à une énergie inférieure, ce qui entraîne une légère diminution pour I ₂ et augmenter pour I ₁ et Je ₃ dans les bandes interdites indirectes. En présence de la contrainte de traction, le CBM diminue énormément tandis que le VBM monte doucement. La bande interdite indirecte présente ainsi une diminution notable et diminue fortement lorsque la contrainte de traction atteint 6%. Par rapport à celui de la monocouche contrainte Janus WSSe [34], les bandes interdites de I₁ et moi₃ montrent une évolution généralement similaire avec les modulations de déformation en compression et en traction, tandis que la bande interdite de I₂ se comporte à l'opposé sous les déformations en compression.

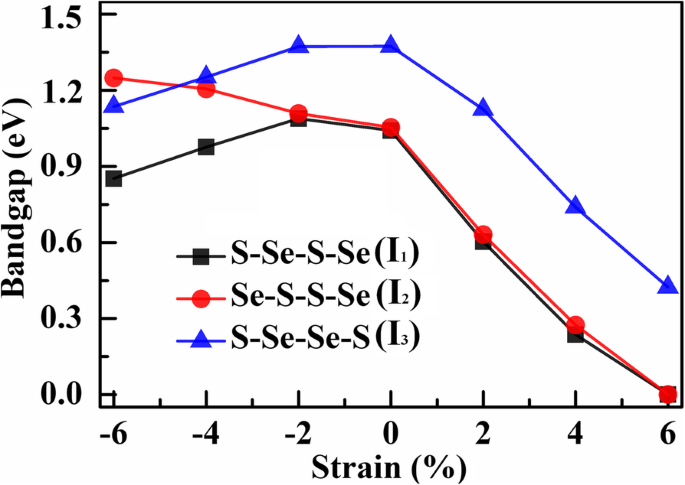
La bande interdite (E _g ) versus les déformations appliquées pour le I ₁ , Je ₂ , et Je ₃ structure

Afin d'avoir un aperçu de la structure électronique de la bicouche WSSe en présence des contraintes, la bande d'énergie projetée des orbitales atomiques est étudiée, comme le montre la Fig. 6. En raison de sa symétrie d'inversion centrale (Fig. 1l), les orbitales des couches supérieure et inférieure pour I ₃ sont de l'énergie dégénérée, qui contribuent de manière identique à la structure de la bande. Au contraire, à cause de l'asymétrie d'inversion de structure de I ₁ et Je ₂ , les orbitales des couches supérieure et inférieure sont divisées. Les résultats ci-dessus suggèrent qu'il existe une corrélation positive entre la dégénérescence et la symétrie structurelle. En raison de la symétrie d'inversion centrale de I ₃ empilement, les orbitales des couches supérieure et inférieure pour I ₃ sont des dégénérescences énergétiques, qui contribuent de manière identique à la structure de la bande, quelles que soient les différentes déformations. Comme le montre la figure 6g–i, le CBM et le VBM sont également dérivés des deux couches WSSe. Au contraire, à cause de l'asymétrie d'inversion structurelle de I₁ et moi₂ , les orbitales des deux couches sont séparées, comme le montrent les figures 6a–c et 6d–f. L'original Je ₁ La structure présente une hétérostructure typique de type II, avec le CBM et le VBM provenant des couches inférieure et supérieure de WSSe Janus, respectivement. L'alignement de la bande ne varie pas sous les contraintes de compression ou de traction (Fig. 6a–c). Quant au Je ₂ empilement sans et avec une contrainte de compression, le CBM provient à la fois des deux couches, et le VBM provient de la couche supérieure (Fig. 6d, e). Le Je ₂ l'hétérostructure passe à un alignement de bande de type II sous la contrainte de traction (Fig. 6f), ce qui indique une perspective prometteuse pour le développement de dispositifs de conversion optoélectrique et de stockage d'énergie à haute performance [35].

Bandes d'énergie projetées orbitales atomiques de I ₁ , Je ₂ , et Je ₃ structures sous les déformations de − 4%, 0 et 4%, respectivement. Les couleurs bleu et rouge signifient les contributions orbitales des couches supérieure et inférieure, respectivement

Pour explorer davantage l'effet de couplage spin-orbite (SOC) dans l'ingénierie des déformations dans la bicouche WSSe, les structures de bande en tenant compte du SOC sont en outre calculées sans et avec les déformations de - 4% et 4%, comme le montre la Fig. 7. On constate que, pour les trois configurations, les structures de bandes comprenant les positions de moment de VBM et de CBM, les bandes interdites et les distributions de bandes montrent une tendance d'évolution similaire avec les différentes déformations. Cela suggère que la régularité de la modulation de la contrainte persiste et que l'effet SOC n'influence évidemment pas les principales conclusions.

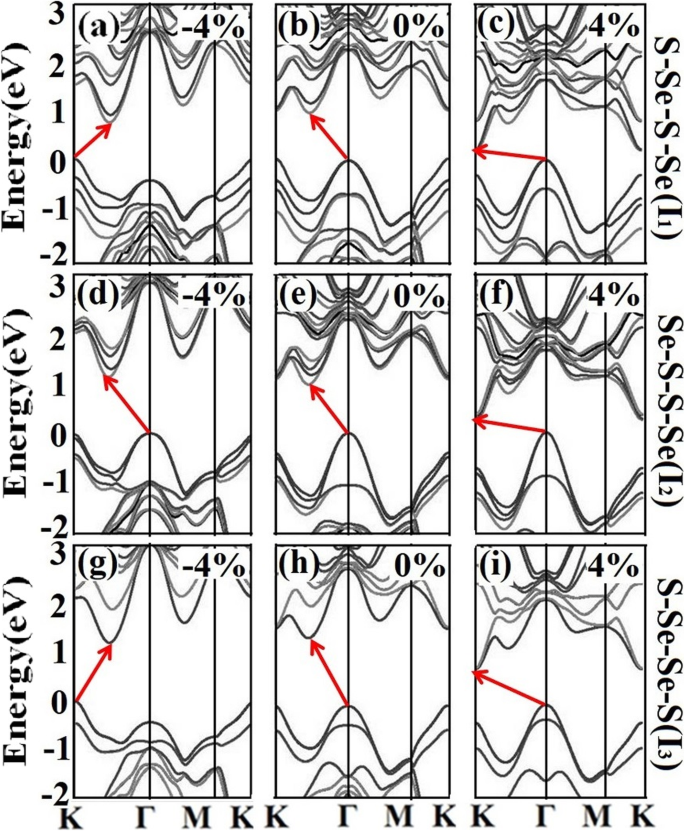
un –je Structures de bande de I ₁ , Je ₂ , et Je ₃ sous les déformations de - 4 %, 0 et 4 % en tenant compte de l'effet SOC, où les couleurs noir et soufflé signifient respectivement les rotations vers le haut et vers le bas. Les bandes interdites sont indiquées par les flèches rouges

Dans le but de moduler les propriétés optiques de la bicouche WSSe, la réponse de la fonction diélectrique sous contrainte externe variable est étudiée. La figure 8 affiche la fonction diélectrique complexe ^” _xx (ε ^” _aa ) et ^” _zz de la bicouche WSSe par rapport à la contrainte appliquée. ^” _xx (ε ^” _aa ) se déplace vers des énergies inférieures avec l'augmentation de la contrainte de traction, et au contraire, se déplace vers la région d'énergie supérieure lorsqu'une contrainte de compression est appliquée. Par rapport à la bicouche WSSe non contrainte avec la transition dipolaire de 0,79, 1,18 et 1,15 eV, respectivement pour I ₁ , Je ₂ , et Je ₃ structures, la modulation de contrainte est capable d'obtenir une large gamme d'énergie de transition de 0,24 à 1,47 eV dans le proche infrarouge et le moyen infrarouge, ce qui pourrait offrir des possibilités étendues pour des détecteurs assortis, par exemple, un détecteur infrarouge et un détecteur pyroélectrique.

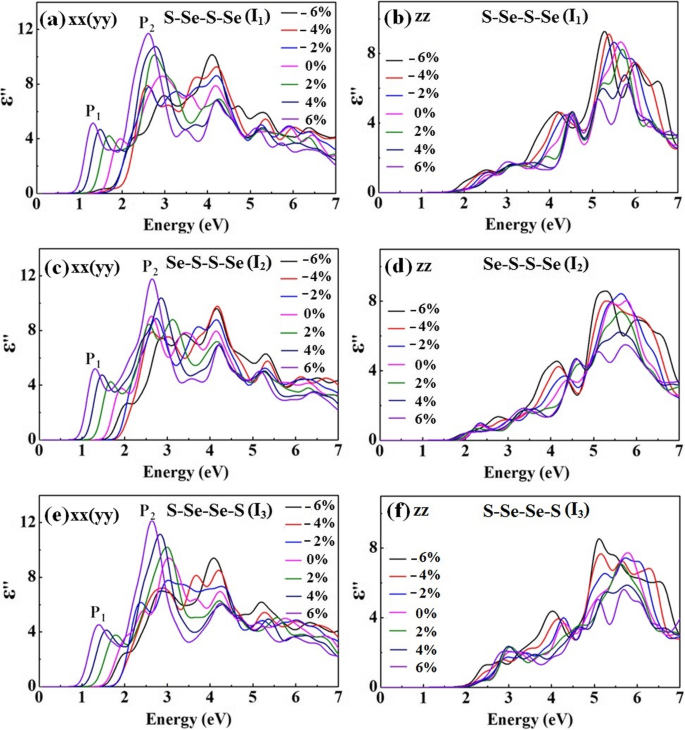
Les parties imaginaires de la fonction diélectrique optique calculée ^” _xx (ε ^” _aa ) et ^” _zz pour Je ₁ (un , b ), Je ₂ (c , d ), et Je ₃ (e , f ) WSSe bicouche par rapport à la contrainte appliquée, respectivement

Les principaux pics dans la partie imaginaire de la fonction diélectrique étiquetée P ₁ et P ₂ sur la figure 8a, c et e pourraient être attribués aux principales transitions interbandes. Ceci est obtenu en ajustant les énergies de crête de la Fig. 8 avec celles des transitions interbandes de la Fig. 4. Lorsqu'une contrainte allant de − 6 à 6% est appliquée, les énergies de crête de P ₁ et P ₂ augmenter d'abord puis diminuer. Quelles que soient les souches, à la fois le P ₁ et P ₂ les pics se situent dans la gamme d'énergie de 1,3 à 3,0 eV, qui présentent une réponse améliorée dans un large spectre allant de l'ultraviolet, visible à la zone proche infrarouge. Les pics largement distribués devraient convenir à la conception d'émetteurs de métamatériaux multibandes avec des applications photoélectriques prometteuses.

L'anisotropie contrôlable de la bicouche WSSe à travers l'ingénierie des contraintes est étudiée plus en détail. Comparé à celui de ε ^” _xx (ε ^” _aa ), ^” _zz présente une variation insignifiante quelle que soit la contrainte de traction ou de compression. Cela manifeste le fait que la partie imaginaire de la fonction diélectrique possède des propriétés de réponse différentes avec l'augmentation de la déformation. Sans la contrainte, le ε ^” _xx (ε ^” _aa ) et ^” _zz sont une anisotropie avec une préférence de transformation E||ĉ pour tous les I ₁ , Je ₂ , et Je ₃ structure. Pour I ₁ ou Je ₃ , tandis qu'une contrainte de compression est appliquée, l'anisotropie de la transition dipolaire est d'abord renforcée puis affaiblie et celle avec la contrainte de traction est toujours renforcée. Néanmoins, l'anisotropie de I ₂ est renforcée avec l'augmentation de la contrainte de traction et s'affaiblit une fois qu'une contrainte de compression est introduite. Une isotropie de transition dipolaire se produit lorsque la déformation compressive continue d'augmenter jusqu'à − 6%~− 4%, où E||ĉ et E⊥ĉ possèdent une préférence de transformation égale. Ainsi, la bicouche WSSe avec une modulation de contrainte appropriée conduira à une transition de l'anisotropie optique à l'isotropie. Étant donné que l'effet excitonique joue généralement un rôle important dans l'absorption optique [36, 37], la préférence de transition dipolaire déterminée par la fonction diélectrique peut être explorée pour les applications optoélectroniques potentielles avec un processus d'électroluminescence.

Comme il a été démontré que certaines monocouches TMDC typiques avec une phase 2H ont les mêmes réseaux hexagonaux et des caractères similaires dans leurs structures de bandes monocouches [5, 33, 38, 39]. Par conséquent, la monocouche et la bicouche Janus dérivées de ces matériaux TMDC, tels que le MXY (M =Mo ou W, X /Oui =S, Se ou Te, et X ≠ Oui ), devrait posséder des structures de bande similaires [8, 32] et donc des propriétés électroniques et optiques similaires, ainsi qu'une tendance à l'évolution avec la modulation de contrainte. Par conséquent, les principaux résultats de calcul auront une certaine universalité dans les matériaux 2H-TMDC Janus. En parcourant les rapports précédents, les propriétés mécaniques du MoS plié hors plan₂ des films minces ont été révélés [40], les propriétés électroniques et optiques des composés TMDC ont été étudiées [22], et les écarts énergétiques des TMDC monocouches et hétérobicouches Janus ont été démontrés pour contrôler le champ électrique [41]. En comparant ces travaux, nous fournissons une série de résultats innovants dans les propriétés électroniques et optiques modulées en déformation de la bicouche Janus WSSe 2D, qui enrichit la connotation physique des matériaux Janus et fournit une stratégie de contrôle prometteuse vers l'application de la prochaine génération électronique et nanodispositifs optoélectroniques.

Conclusion

En résumé, la dépendance en déformation des propriétés électroniques et optiques de la bicouche WSSe est systématiquement étudiée. En comparant les énergies de liaison de différents empilements, la configuration la plus favorable de la bicouche WSSe est déterminée. La bicouche WSSe conserve une structure de bande interdite indirecte, sensible aux contraintes externes. La bande interdite de toutes les structures stables peut être adaptée du semi-conducteur à la métallicité sous pour obtenir un large spectre dans le proche infrarouge et le moyen infrarouge. Les bandes d'énergie projetées des orbitales atomiques révèlent une corrélation positive entre la dégénérescence et la symétrie structurelle, ce qui explique les évolutions de la bande interdite. La préférence de transition dipolaire est étudiée à partir des propriétés diélectriques et ajustée par la déformation biaxiale. Sous environ − 6%~− 4% de déformation critique, une transformation contrôlable entre les propriétés optiques anisotropes et isotropes est réalisée. Les comportements électroniques et optiques modulés en contrainte de la bicouche Janus WSSe possèdent une large perspective d'application dans les nanodispositifs électroniques et optoélectroniques de nouvelle génération.

Disponibilité des données et des matériaux

Toutes les données générées ou analysées au cours de cette étude sont incluses dans cet article publié.

Abréviations

2D :

Bidimensionnel

CBM :

Bande de conduction minimum

DFT :

Théorie fonctionnelle de la densité

SOC :

Couplage spin-orbite

TMDC :

Dichalcogénures de métaux de transition

VBM :

Bande de cantonnière maximum