Pseudomagnetorésistance de vallée à commande électrique dans le graphène avec distorsion du réseau de Kekulé en forme de Y
Résumé
Nous proposons une nouvelle méthode pour réguler la pseudomagnétorésistance de vallée dans des transistors à effet de champ à base de graphène balistique en tenant compte de la distorsion du réseau de Kekulé en forme de Y et de la barrière électrique. Le dispositif implique l'injection de vallée et la détection de vallée par une source et un drain de contrainte ferromagnétique. La manipulation de la vallée dans le canal est réalisée via la distorsion du réseau de Kekulé en forme de Y et la barrière électrique. Le mécanisme central de ces dispositifs repose sur la distorsion du réseau de Kekulé en forme de Y dans le graphène qui peut induire une précession de vallée, contrôlant ainsi l'orientation de la vallée des électrons du canal et donc le courant collecté au niveau du drain. Nous avons constaté que la tension de polarisation externe de réglage fait osciller la pseudomagnétorésistance de vallée entre des valeurs positives et négatives et qu'une pseudomagnétorésistance de vallée à effet tunnel colossale de plus de 30 000 % peut être obtenue. Nos résultats suggèrent que la synergie de la valleytronics et des logiques numériques peut fournir de nouveaux paradigmes pour le traitement de l'information basé sur la valleytronic et l'informatique réversible.
Introduction
Le graphène, étant une feuille bidimensionnelle d'atomes de carbone, qui a une excellente mobilité des porteurs et offre le canal le plus mince possible pour l'utilisation de la conception de transistors à effet de champ métal-oxyde-semi-conducteur [1]. Semenov a proposé un transistor à effet de champ de spin en utilisant une couche de graphène comme canal [2], ce qui implique l'injection de spin et la détection de spin par source ferromagnétique et drain, et la manipulation de spin dans le canal est réalisée via un contrôle électrique de l'échange d'électrons. interaction avec une grille ferromagnétique. De plus, l'interaction spin-orbite de Rashba est un autre outil prometteur pour le contrôle du spin dans le graphène [3]. L'interaction spin-orbite de Rashba peut induire une précession de spin, contrôlant ainsi l'orientation de spin des électrons du canal. Les transistors à effet de champ de spin ont également inspiré de nombreuses idées de recherche importantes, telles que la magnétorésistance géante et la magnétorésistance tunnel [3, 4]. La magnétorésistance géante et la magnétorésistance tunnel peuvent être appliquées dans les technologies de stockage numérique et de capteurs magnétiques.
D'autre part, les électrons de Dirac dans le graphène possèdent un degré de liberté de vallée supplémentaire en plus des équivalents conventionnels de charge et de spin. En raison de la grande différence de quantité de mouvement entre les deux vallées et de la suppression de la diffusion par intervalles dans des échantillons de graphène propres [5-7], on pense que le degré de liberté de la vallée exerce le même effet que le spin électronique dans le transport et la manipulation d'informations, ce qui conduit à une nouvelle discipline s'élevant sous le nom de valleytronics. Dans l'analogue du transistor à effet de champ de spin, le transistor à effet de champ de vallée est également théoriquement proposé dans le graphène [8], qui consiste en un canal quantique unidimensionnel de graphène avec espacement pris en sandwich entre deux nanorubans de graphène fauteuil (source et drain); ensuite, un champ électrique de grille latérale est appliqué au canal et module la polarisation de vallée des porteurs en raison de l'interaction vallée-orbite, contrôlant ainsi la quantité de courant collecté au niveau du drain. Cependant, en raison du fait que le couplage vallée dans le graphène n'est pas devenu une réalité physique depuis longtemps, il existe peu d'études supplémentaires basées sur les transistors à effet de champ vallée du graphène et les études connexes. Des expériences récentes de Gutierrez et al. [9] ont révélé une texture de liaison Kekulé(Kek-Y) en forme de Y inhabituelle dans le réseau en nid d'abeille sur un super-réseau de graphène-cuivre, où l'un des six atomes de carbone dans chaque maille unitaire du super-réseau n'a pas d'atomes de cuivre en dessous et acquiert une plus courte obligation du plus proche voisin. De plus, Gamayun a montré que la texture de la liaison Kek-Y offre un moyen pour une précession de vallée contrôlée par la quantité de mouvement [10]. Beenakker et al. [11] ont montré que le système Kek peut faire apparaître un effet de retournement de vallée via la réflexion de type Andreev. Récemment, Wang et al. [12] ont trouvé que la modulation de longueur de liaison C-C du réseau de Kekulé qui maintient la symétrie d'inversion du système peut être utilisée pour manipuler le degré de liberté de la vallée d'une manière similaire au champ d'échange précédant le spin. Cela permet de concevoir un nouveau type de transistor à effet de champ vallée en graphène. De plus, il n'y a aucun rapport sur les effets combinés de la distorsion du réseau Kek-Y sur la pseudomagnétorésistance de la vallée dans le graphène. La pseudomagnétorésistance Valley [13, 14] est analogue à la magnétorésistance dans la jonction tunnel magnétique [15] où l'amplitude du courant de spin dépend de l'orientation magnétique des électrodes [4].
Méthodes
Dans ce travail, nous proposons un nouveau type de transistors à effet de champ vallée (VFET) pour les électrons à base de graphène. La conception du dispositif suppose une source/drain de contrainte ferromagnétique (FM-S) pour l'injection/détection polarisée en vallée, qui ressemble à un transistor à spin conventionnel (voir Fig. 1a). La rotation de la vallée dans le canal du graphène repose sur le super-réseau de graphène Kek-Y [10-12], qui peut être obtenu par un super-réseau de graphène épitaxié sur Cu(111), avec les atomes de cuivre en concordance avec les atomes de carbone [9]. Cependant, il manque des atomes de cuivre sous certains atomes de carbone, ce qui entraîne des lacunes périodiques d'atomes de cuivre apparaissant sous le graphène. Une telle lacune d'atome de substrat conduit à la contraction de trois liaisons voisines. Ici, nous utilisons δ t pour représenter la modification énergétique du saut de l'électron correspondant à ces trois liaisons. Nous supposons que le graphène ferromagnétique est constitué de la même bande métallique FM. Les deux aimantations de la source et du drain sont dirigées suivant la direction du courant (le x axe), qui peut être dans l'alignement parallèle (P) ou antiparallèle (AP), à l'aide d'un champ magnétique externe dans le plan. Dans la jauge de Landau, le potentiel vecteur magnétique issu du champ de franges a la forme [16, 17] \(A(r)=A_{y}(x)\overrightarrow {y}\) avec A y (x )=A y [Θ (−x )±Θ (x −L )], où le signe plus (moins) correspond à la configuration P(AP) des aimantations, Θ (x ) est la fonction de pas de Heaviside. D'autre part, nous supposons que la même contrainte est appliquée sur la source et le drain des VFET, ce qui peut être induit par une tension sur le substrat du graphène [18]. La déformation élastique peut être traitée comme une perturbation des amplitudes de saut et agit comme un potentiel de jauge A S (r ). La tension est réglée le long du x direction, dans ce cas, A S (r ) uniforme le long du y axe [16]. Pour plus de précision, nous prenons un profil lisse typique de son y composant en tant que A Sy (x )=A S [Θ (−x )+Θ (x −L )], où A S est l'amplitude. De plus, une barrière électrique est également appliquée dans la région du réseau Kek-Y, qui peut être réglée par une tension de polarisation externe.
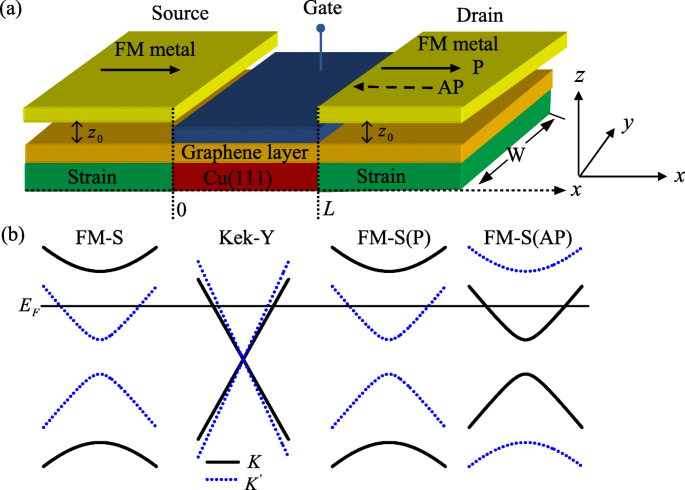
un Illustration schématique du VFET utilisant un canal de graphène avec une distorsion de réseau Kek-Y et une polarisation de grille, qui contrôle l'orientation de la vallée des électrons du canal. La source et le drain sont en graphène FM-S, qui injecte et détecte des électrons dans une polarisation spécifique. Où z 0 est la distance entre la couche de graphène et la bande FM. L est la longueur du canal, W est la largeur de l'échantillon de graphène dans le y direction, et W ≫L . b Structure de bande à proximité des pointes de Dirac. La ligne horizontale indique l'énergie de Fermi (couleur en ligne)
La propagation des quasiparticules d'excitation de faible énergie dans les VFET avec des super-réseaux de graphène Kek-Y peut être décrite par le hamiltonien à particule unique suivant [10–12]
$$ \begin{array} [c]{ll} H=&v_{F}(\mathbf{P}\cdot\sigma)+v_{\tau}(\mathbf{P}\cdot\tau)\Theta \left(x\right) \Theta\left(Lx\right) +\\ &U\sigma_{0}\tau_{0}\Theta\left(x\right) \Theta\left(Lx\right) + A_{M}(x)\sigma_{y}+\tau_{z}A_{S}(x)\sigma_{y}. \end{tableau} $$ (1)Ici, σ et τ sont les matrices de Pauli pour le sous-réseau et la vallée, respectivement. P =(p x ,p y ) est la quantité de mouvement des électrons de Dirac sans masse, τ z =±1 pour K et \(K^{^{\prime }}\) vallées, v F =10 6 m/s est la vitesse des électrons de Dirac dans le graphène vierge, et v τ v F δ t /3t est le terme de modification de vitesse à partir de l'effet de contraction de la liaison dans le réseau Kek-Y [12], où t est l'énergie de saut entre les villes voisines les plus proches pour le graphène vierge. U est la barrière de potentiel accordable par la porte. Un M (x )=e v F Un y (x ) [19]. Les valeurs propres de l'hamiltonien dans le graphène avec distorsion du réseau Kek-Y et barrière électrique sont données par
$$ E_{\alpha,\beta}=U+\alpha(\hbar v_{F}+\beta\hbar v_{\tau})\sqrt{k_{x\beta} ^{2}+k_{y} ^{2}}. $$ (2)Ici, α =+1(−1) spécifie la bande de conduction (valence). β =±1 désigne les deux sous-bandes divisées en vallée des bandes de conduction et de valence. En raison de l'invariance de traduction dans le y direction, le vecteur d'onde transverse k y est conservé. Les états propres dans le graphène avec la distorsion homogène du réseau Kek-Y sont caractérisés par \(\Psi _{\beta }^{\pm }(k_{x\beta },k_{y})=\frac {1}{ N_{\beta }}\left (1,P_{\beta }^{\pm },Q_{\beta } ^{\pm },R_{\beta }^{\pm }\right)^{T} \), où N β est la constante de normalisation \(N_{\beta }=\left (1+P_{\beta }^{2}+Q_{\beta }^{2}+R_{\beta }^{2}\right)^ {\frac {1}{2}}\) et \(P_{\beta }^{\pm }, Q_{\beta }^{\pm }\), et \(R_{\beta }^{\ pm }\) sont des fonctions définies comme suit :
$$ \begin{array} [c]{cc} P_{\beta}^{\pm}=&\frac{(EU)^{2}+\left(\hbar^{2}v_{F}^ {2}-\hbar^{2}v_{\tau} ^{2}\right)\left(k_{x\beta}^{2}+k_{y}^{2}\right)}{2 (UE)\hbar v_{F}(\pm k_{x\beta}-{ik}_{y})},\\ Q_{\beta}^{\pm}=&\frac{(UE)^ {2}-\left(\hbar^{2}v_{F}^{2}-\hbar^{2}v_{\tau} ^{2}\right)\left(k_{x\beta}^ {2}+k_{y}^{2}\right)}{2(EU)\hbar v_{\tau}(\pm k_{x\beta}-{ik}_{y})},\\ R_{\beta}^{\pm}=&\frac{(UE)^{2}-\left(\hbar^{2}v_{F}^{2}+\hbar^{2}v_{\ tau} ^{2}\right)\left(k_{x\beta}^{2}+k_{y}^{2}\right)}{2\hbar^{2}v_{F}v_{\ tau}(\pm k_{x\beta} -{ik}_{y})^{2}}. \end{tableau} $$ (3)La probabilité de transmission de \(K^{^{\prime }}\) valley à \(K(K^{^{\prime }})\) valley \(T_{K^{^{\prime }}, K(K^{^{\prime }})}\) peut être calculé en utilisant la technique de la matrice de transfert [20]. D'après la formule de Laudauer-Btittiker, la conductance dépendante de la vallée est donnée par [21] :
$$ G_{K^{^{\prime}},K(K^{^{\prime}})}=G_{0} {\int_{-\frac{\pi}{2}}^{\ frac{\pi}{2}}} T_{K^{^{\prime}},K(K^{^{\prime}})}\cos(\phi_{0})d\phi_{0} . $$ (4)Ici \(G_{0}=2e^{2}W/\left (v_{F}\pi ^{2}\hbar ^{2}\right)\left \vert E\right \vert \), W est la largeur de l'échantillon de graphène dans le y direction, et ϕ 0 est l'angle incident par rapport au x direction.
Avant de procéder aux calculs, nous discutons de la structure de la bande avec k y =0, comme le montre la figure 1b. Dans la région source FM-S, la bande d'énergie du graphène s'écrit \(E=\alpha \sqrt {(\hbar v_{F}k_{x})^{2} +(A_{M}+\tau _{z}A_{S})^{2}}\). On peut constater que la vallée dégénère en soulèvement et différents écarts sont induits au niveau du K et \(K^{^{\prime }}\) points car le potentiel vecteur total A M +A S agissant sur K électrons est supérieur au potentiel vectoriel total |A M −A S | agissant pour \(K^{^{\prime }}\) électrons [19]. Cela indique que seuls les électrons \(K^{^{\prime }}\) peuvent traverser la région source FM-S lorsque l'énergie incidente est située dans |A M −A S |<E <Un M +A S [22, 23]. De même, dans la région de drain FM-S, la bande d'énergie du graphène peut être écrite comme \(E=\alpha \sqrt {(\hbar v_{F}k_{x})^{2}+(\pm A_{ M}+\tau _{z}A_{S})^{2}}\), où le signe ± correspond à la configuration P et AP des aimantations. Ainsi, seuls les électrons \(K^{^{\prime }}\) sont détectés dans la structure P et seulement K les électrons sont détectés dans la structure AP lorsque l'énergie de Fermi se situe dans la plage de [|A M −A S |,A M +A S ]. Dans le canal du graphène, la vallée dégénérée est également liftée, mais il existe une différence importante. Contrairement au cas principal, où les phases de K et les composantes \(K^{^{\prime }}\) évoluent avec le même vecteur d'onde [ie, \(k=E/\hbar v_{F}\)], maintenant, elles évoluent séparément avec des vecteurs d'onde différents ( \(k_{+}=(UE)/(\hbar v_{F}+\hbar v_{\tau })\) et \(k_{-}=(UE)/(\hbar v_{F}-\ hbar v_{\tau })\)) dû aux super-réseaux de graphène Kek-Y mélangeant la vallée (voir Eq. 2). Cela conduit à la précession de la vallée des électrons du canal dans l'espace de la vallée [12]. La précession de vallée dans le graphène est à la base du transistor à effet de champ de vallée [8]. Et la précession de vallée peut également être caractérisée par une pseudomagnétorésistance de vallée (VPMR) dans les jonctions FM-S/Kek-Y/FM-S, analogue à la magnétorésistance dans les jonctions à effet tunnel quantique à base de graphène avec l'interaction spin-orbite [4] , qui est défini comme \(VPMR=\frac {G_{P}-G_{AP}}{G_{P}}\), où G P et G PA représentent la conductance dans les configurations P et AP, respectivement, et \(G_{P}=G_{K^{^{\prime }},K^{^{\prime }}}, G_{AP}=G_{K ^{^{\prime }},K}\). L'amplitude du courant de vallée dépend de l'orientation magnétique de la source et du drain dans notre appareil considéré.
Résultats numériques et discussions
Dans ce qui suit, nous présentons les résultats numériques pour la jonction FM-S/Kek-Y/FM-S dans le graphène. Tout au long de l'article, nous définissons la longueur du canal L =207nm, et restreindre l'énergie de Fermi à 20 meV<E <140meV, supposé satisfaisant |A M −A S |<E <Un M +A S . Les figures 2a et b montrent les résultats calculés de la conductance tunnel et du VPMR en fonction de v t avec Fermi énergie E =80meV et barrière de potentiel rectangle U =−10meV. Nous pouvons trouver que G P et G PA ont les mêmes périodes d'oscillation mais les phases inverses. Par conséquent, le VPMR oscille avec l'augmentation de v t et la valeur négative VPMR peut apparaître. Ces phénomènes sont similaires au cas de la magnétorésistance dans les jonctions à effet tunnel quantique à base de graphène balistique avec l'interaction spin-orbite [4]. Les caractères d'oscillation de la conductance de G P et G PA peut s'expliquer par la différence de phase entre les deux composantes de la vallée. Lorsque l'angle d'incidence ϕ 0 =0, le déphasage est donné par :\(\Delta \theta =(k_{x+}-k_{x-})L=-\frac {2(EU)v_{\tau }}{\hbar (v_ {F}^{2}-v_{\tau }^{2})}L\). Δ θ détermine l'orientation de la polarisation de la vallée avant que l'électron n'entre dans le drain, par rapport à celle de l'état du drain [8]. Pour Δ θ =±2n π ,n =1,2,3⋯, les deux polarisations sont alignées, conduisant à la conductance G P maximum et VPMR une valeur positive élevée (comme on le voit dans v τ =0,022, 0,033). Par contre, pour Δ θ =±(2n +1)π ,n =0,1,2⋯, ils sont orthogonaux entre eux, conduisant à la conductance G PA minimum et VPMR négatif (comme on le voit dans v τ =0,0167, 0,027, 0,038).
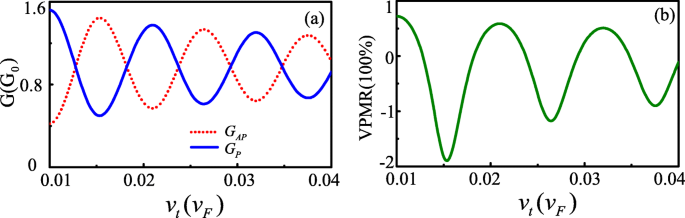
Conductance G P ,Un P et VPMR contre v t à L =207nm,E =80meV et U =−10meV (couleur en ligne)
La conductance et la VPMR ne sont pas seulement des fonctions d'oscillation de la modification de l'énergie de saut, elles oscillent également avec l'énergie de Fermi et le potentiel de barrière effectif puisque Δ θ les échelles sont également linéaires avec l'énergie de Fermi et la barrière de potentiel U . Les figures 3a et b montrent la conductance en fonction de l'énergie de Fermi et du potentiel de barrière effectif, respectivement. Les VPMR correspondantes sont données sur les Fig. 3c et d. Ils présentent tous des caractéristiques d'oscillation variant avec E et U valeur, même lorsque le potentiel de barrière efficace U est supérieure à l'énergie de Fermi E . L'origine physique d'un tel phénomène est liée au tunnel de Klein [12]. Bien qu'il existe des phénomènes d'oscillation similaires de conductance et de VPMR pour une augmentation de E et U , certaines différences peuvent également être trouvées. En tant que E augmente, la différence entre G P et G PA la conductance devient de plus en plus petite, ce qui conduit l'amplitude d'oscillation de VPMR à diminuer avec l'augmentation de l'énergie de Fermi. Sous la condition Δ θ =±n π est satisfait, la différence entre G P et G PA est plus grand avec l'augmentation de U , en particulier à certains endroits, le G P et G PA la conductance présente des caractéristiques de commutation. Les caractères sont plus souhaitables pour l'application de VPMR. Remarquablement, la valeur maximale observée de VPMR est supérieure à 30 000 % à faible E . Cette valeur dépasse largement le MR de ~ 175% dans les jonctions à effet tunnel quantique à base de graphène balistique avec l'interaction spin-orbite [4] et la pseudomagnétorésistance de ~ 100% dans du graphène bicouche contrôlé par des portes externes [24], ce qui est encore plus grand que le VPMR de ~ 10000% dans un système de cônes de Dirac fusionnant [13].
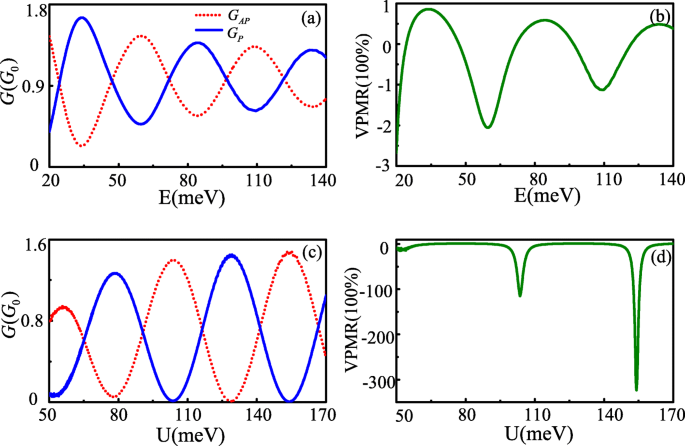
Conductance G P ,Un P (un , c ) et VPMR (b , d ) en fonction de l'énergie de Fermi et de la barrière électrique à L =207nm,v t =0.02v f . les autres paramètres sont U =−10meV pour a et c , E =80meV pour b et d (couleur en ligne)
Conclusions
En conclusion, nous avons proposé un type de transistors à effet de champ vallée pour les électrons à base de graphène et étudié la pseudomagnétorésistance vallée à travers celui-ci. Nous avons montré que la caractéristique d'oscillation de la pseudomagnétorésistance de vallée n'est pas seulement liée à la modification de l'énergie de saut et à l'énergie de Fermi, mais peut également être largement ajustée par le potentiel de barrière effectif. La pseudomagnétorésistance de vallée réglée par une tension de polarisation externe profite au dispositif de transistor à effet de champ de vallée, et nous prévoyons que les dispositifs quantiques de vallée à commande électrique proposés ici peuvent jouer un rôle dans les ordinateurs hybrides quantiques et quantiques-classiques.
Des recherches supplémentaires pourraient impliquer les différentes contraintes (uniaxiales vs biaxiales) réglables, la diffusion de la vallée des électrons et le transport dans nos transistors à effet de champ à base de graphène proposés, car la coloration est utile pour contrôler le degré de diffusion par intervalles dans les motifs de Kekulé [25] . Ensuite, d'autres matériaux bidimensionnels (MoS2 , WS2 , WSe2 , etc.) les analogues du graphène peuvent également fournir une plate-forme intéressante pour d'autres transistors à effet de champ à base de matériaux bidimensionnels avec une distorsion en réseau de Kekulé en forme de Y.
Disponibilité des données et des matériaux
Les ensembles de données soutenant les conclusions de cet article sont inclus dans l'article.
Abréviations
- AP :
-
Antiparallèle
- FM-S :
-
Déformation ferromagnétique
- Kek-Y :
-
Kekulé en Y
- P :
-
Parallèle
- VFET :
-
Transistors à effet de champ Valley
- VPMR :
-
Pseudomagnétorésistance Valley
Nanomatériaux
- Treillis :MachX03D FPGA améliore la sécurité avec des capacités matérielles de racine de confiance
- Le graphène met les nanomatériaux à leur place
- Graphène dans les haut-parleurs et les écouteurs
- Nanoruban de graphène
- RGO et réseaux tridimensionnels de graphène co-modifiés TIM avec de hautes performances
- Évaluation des structures graphène/WO3 et graphène/CeO x en tant qu'électrodes pour les applications de supercondensateurs
- Aérogel de graphène/polyaniline avec superélasticité et haute capacité en tant qu'électrode de supercondensateur hautement tolérante à la compression
- Synthèse écologique et facile de nanofils de Co3O4 et leur application prometteuse avec du graphène dans les batteries lithium-ion
- Nanocomposites à base d'oxyde de graphène décorés de nanoparticules d'argent en tant qu'agent antibactérien



