Prédiction et analyse efficaces du piégeage optique à l'échelle nanométrique via la méthode de déchirement et d'interconnexion par éléments finis

Introduction

Les pincettes optiques plasmoniques basées sur les plasmons de surface (SP) attirent beaucoup d'attention et ont été largement appliquées pour capturer des nanoparticules [1,2,3,4,5,6]. SP est un phénomène de résonance causé par le couplage de la lumière incidente avec une longueur d'onde spécifique et des électrons libres à l'interface des métaux et des diélectriques [7]. Les SP permettent à la pince à épiler optique de franchir la limite de diffraction. De plus, l'amélioration drastique du champ local des SP peut réduire la demande d'intensité de la lumière incidente [7, 8]. Cependant, les SP sont étroitement liés au matériau et aux dimensions des objets ainsi qu'à la longueur d'onde de la lumière incidente, ce qui nécessite un grand nombre d'expériences pour déterminer les paramètres optimaux des pincettes optiques SP en pratique. Sur cette base, la méthode de simulation joue un rôle de plus en plus important en tant que moyen auxiliaire pour la conception et l'optimisation des pincettes optiques SP [9]. Dans ces simulations, le calcul de la force optique est nécessaire pour prédire un piégeage stable. Pour les objets réguliers tels que les sphères, la force optique peut être dérivée analytiquement de la théorie généralisée de Lorenz-Mie [10, 11]. Cependant, pour les objets avec des configurations compliquées, des méthodes numériques qui résolvent les équations de Maxwell de manière rigoureuse sont nécessaires pour modéliser les champs électromagnétiques et la force et le potentiel optiques qui en découlent.

Ces méthodes numériques peuvent être principalement classées en méthodes d'équation différentielle (DEM) et en méthodes d'équation intégrale (IEM) [12,13,14,15]. Par rapport aux IEM, les méthodes d'équation différentielle (DEM) montrent des capacités supérieures à traiter des géométries et des composants complexes. Les DEM ont également l'avantage d'un calcul simple de la distribution en champ proche, qui joue un rôle important dans l'analyse des SP. En tant que DEM représentatif, la méthode du domaine temporel aux différences finies (FDTD) est implémentée dans le domaine temporel, ce qui permet d'obtenir facilement des informations à large bande et des réponses transitoires [16, 17]. Cependant, le FDTD exige un modèle dispersif précis pour décrire les propriétés matérielles dépendantes de la fréquence dans les SP, tandis que la précision de la solution FDTD dépend fortement de la précision d'approximation de ce modèle dispersif [18]. En outre, le FDTD repose sur des maillages structurés, ce qui entraîne souvent des erreurs d'escalier pour les surfaces courbes. En tant qu'autre DEM représentatif, la méthode des éléments finis (FEM) a été largement adoptée car elle peut facilement gérer les matériaux dispersifs dans le domaine fréquentiel et éliminer l'erreur d'escalier par maillage non structuré [19,20,21,22]. Par rapport au FDTD, le FEM peut adopter directement les paramètres de matériaux mesurés sans aucun modèle dispersif approximatif. Cependant, les améliorations drastiques du champ local dans les SP nécessitent des maillages fins dans la discrétisation FEM. De plus, les objets de grandes dimensions et les objets multiples augmenteront considérablement le nombre d'inconnues. Ces facteurs entraîneront des systèmes matriciels mal conditionnés et d'énormes consommations de calcul, ce qui pose de grands défis à la FEM traditionnelle pour l'analyse du piégeage optique amélioré par SP.

Dans cet article, une méthode efficace de déchirure et d'interconnexion d'éléments finis à double primale (FETI-DP) est présentée pour simuler le piégeage optique à l'échelle nanométrique. Le FETI-DP adopte un schéma de décomposition de domaine sans chevauchement, qui divise un problème complexe original à grande échelle en une série de problèmes simples à petite échelle pour les surmonter. Il applique une condition de transmission aux interfaces de sous-domaine pour assurer la continuité du champ et introduit une variable double pour réduire le problème tridimensionnel (3D) d'origine en un problème bidimensionnel (2D) par multiplicateur de Lagrange. Les variables primales aux coins du sous-domaine sont extraites pour accélérer le taux de convergence de la solution itérative du problème dual [23,24,25,26]. Une approche de sparsification de bas rang est développée pour améliorer les performances du FETI-DP. Il utilise des algorithmes à faible densité de données pour améliorer l'efficacité de résolution des problèmes de sous-domaine et du problème dual [27, 28]. La méthode proposée fournit des sous-domaines entièrement découplés, qui permettent la simulation parallèle de la force optique pour piéger les nanoparticules. Le tenseur de contraintes de Maxwell (MST) qui révèle la relation entre le champ électromagnétique et la quantité de mouvement mécanique est adopté pour évaluer la force optique [29]. Sur la base de la force optique obtenue, le potentiel optique peut être encore calculé pour l'analyse d'un piégeage stable. Par rapport aux IEM, la méthode proposée est plus puissante pour traiter les matériaux composés et résoudre le champ proche pour le piégeage optique basé sur SP. Par rapport au FDTD, la méthode proposée peut traiter avec précision les matériaux métalliques dispersifs dans les systèmes de piégeage optique basés sur SP et éliminer l'erreur d'escalier pour les objets avec une limite de courbe. Par rapport à la FEM, la méthode proposée est adaptée au calcul à grande échelle du piégeage optique. Plusieurs exemples sont analysés et les résultats numériques démontrent la précision et l'efficacité de la méthode proposée pour la prédiction et l'analyse du piégeage optique à l'échelle nanométrique.

Méthodes

Formulations FETI-DP

Pour l'implémentation FETI-DP, le domaine de calcul original Ω est d'abord déchiré en une série de sous-domaines non chevauchants Ω ⁱ (i = 1, 2, 3⋯, N _s ), comme le montre la figure 1. Dans chaque sous-domaine Ω ⁱ , un système d'éléments finis de sous-domaine peut être dérivé de l'équation d'onde vectorielle comme

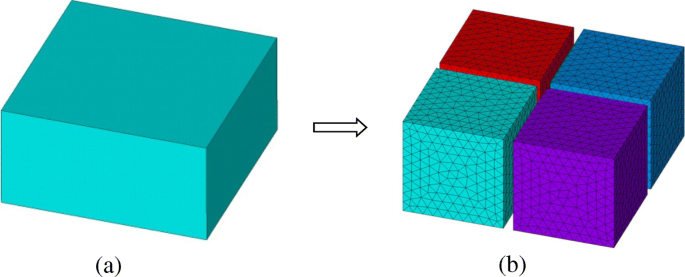
Un schéma de division de domaine avec des sous-domaines non chevauchants dans la méthode FETI-DP. un Domaine d'origine. b Sous-domaines divisés et maillages discrétisés

où E ⁱ désigne le champ électrique inconnu à résoudre dans \( {\Omega}^i \), k ₀ et η ₀ sont respectivement le nombre d'onde en espace libre et l'impédance intrinsèque, et \( {\mathbf{J}}_i^{\mathrm{imp}} \) est le courant imposé. \( {\Gamma}_{\mathrm{ABC}}^i \) signifie la condition limite absorbante (ABC) pour tronquer la région ouverte infinie. Il convient de noter que k ₀ doit être remplacé par l'impédance d'onde dans le milieu si le milieu environnant n'est pas un espace libre, ce qui est courant pour le piégeage optique. A l'interface du sous-domaine Γ ⁱ , une condition aux limites supposée est requise pour générer un problème de valeur aux limites complet dans Ω ⁱ . Ici, une condition de transmission de type Robin avec une variable auxiliaire inconnue Λ _i est imposé comme

où \( {\hat{n}}^i \) désigne un vecteur extérieur normal unitaire à l'interface de sous-domaine Γ ⁱ , et α ⁱ est un paramètre complexe qui peut souvent être choisi comme jk ₀ . Tous les sous-domaines sont ensuite discrétisés par des éléments tétraédriques. Dans chaque élément, nous développons E avec des fonctions de base vectorielles N et coefficient de champ électrique inconnu E comme

où s désigne le nombre de fonctions de base vectorielles dans chaque élément tétraédrique. s est choisi pour être 6 pour la fonction de base traditionnelle d'ordre bas basée sur le bord, alors qu'il est plus grand pour la fonction de base vectorielle d'ordre élevé, puisque des fonctions de base supplémentaires basées sur la face ou le volume sont introduites.

En appliquant la méthode de Galerkin, l'équation matricielle FEM dans Ω ⁱ sur le coefficient de champ électrique inconnu E ⁱ peut être obtenu comme

où les notations en indice c et r distinguer les degrés de liberté d'angle (DOF) et les DOF ​​restants, ce qui extrait les DOF ​​d'angle en tant que variable primale pour construire le schéma dual-primal (DP). Ici, K est la matrice du système FEM et f est le vecteur d'excitation. B est une matrice booléenne qui extrait les DDL d'interface d'un sous-domaine. λ est une variable double générée en développant Λ _i , également appelé multiplicateur de Lagrange.

Ensuite, les sous-domaines adjacents peuvent être interconnectés en appliquant la continuité du champ électrique tangentiel et du champ magnétique aux interfaces. Nous assemblons toutes les interfaces de sous-domaine et éliminons toutes les inconnues internes de sous-domaine E ⁱ . Une équation d'interface globale réduite sur la variable double λ peut être obtenu comme

L'équation (6) peut être résolue par des méthodes itératives, telles que la méthode des résidus minimaux généralisés (GMRES). \( {\tilde{\mathbf{K}}}_{cc} \) est le système de coin global, qui peut accélérer la convergence itérative dans l'espace primal. Un préconditionneur approprié peut être utilisé pour améliorer le taux de convergence itérative, tel qu'une décomposition LU inverse approximative et incomplète. Une fois la variable double λ est résolu, le champ électrique à l'intérieur de chaque sous-domaine peut être évalué indépendamment par (5). Pour la construction de la matrice globale \( {\tilde{\mathbf{K}}}_{rr} \), il faut construire le sous-domaine numérique fonction de Green \( {\mathbf{Z}}_{rr}^ i \) avec une forme de

où l'inverse de la matrice FEM du sous-domaine \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \) est inclus. Par ailleurs, pour les matrices \( {\tilde{\mathbf{K}}}_{rc} \), \( {\tilde{\mathbf{K}}}_{cr} \), et \( {\tilde {\mathbf{K}}}_{cc} \) et les vecteurs \( {\tilde{f}}_r \) et \( {\tilde{f}}_c \), le \( {\left({ \mathbf{K}}_{rr}^i\right)}^{-1} \) doit être calculé. Les constructions de \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \) au stade de pré-traitement ainsi que leurs produits matrice-vecteur (MVP) à l'étape de solution itérative est coûteuse en temps de calcul. Bien que \( {\mathbf{K}}_{rr}^i \) soit clairsemé, \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \ ) sont denses, ce qui signifie des coûts de calcul élevés. Ensuite, une méthode de sparsification de bas rang est introduite pour accélérer le calcul de \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \). Étant donné que certaines sous-matrices du système d'interface global peuvent être représentées sous forme de matrice de bas rang, leur calcul peut être effectué avec un algorithme de bas rang, ce qui améliore les performances du FETI-DP. On peut voir que le FETI-DP fournit des opérations de sous-domaine indépendantes, de sorte qu'il peut exploiter le calcul parallèle pour améliorer l'efficacité. Pour un schéma parallèle efficace, un principe de division de domaine est de rendre le nombre de DOF dans chaque sous-domaine aussi équilibré que possible. Par conséquent, la taille des sous-domaines doit être liée à la densité de discrétisation du maillage. Habituellement, les petits sous-domaines sont adoptés dans des zones à mailles fines, tandis que les grands sous-domaines sont adoptés dans des zones à mailles grossières.

Sparsification de bas rang

Une approche de sparsification de bas rang est proposée pour fournir un moyen avec peu de données d'améliorer l'efficacité de FETI-DP. Ici, données rares signifie que ces matrices ne sont en fait pas clairsemées mais elles sont clairsemées dans le sens où certains sous-blocs d'entre eux peuvent être représentés par des formes de matrice de décomposition de bas rang comme

où X et O sont sous des formes matricielles complètes, et le rang k est beaucoup plus petit que m et n . La matrice \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \) peut être représentée par des formes matricielles creuses car elle possède la propriété matricielle d'une intégrale opérateur. Par conséquent, à condition que \( {\left({\mathbf{K}}_{rr}^i\right)}^{-1} \) possède une propriété de bas rang dans un sous-domaine donné, il peut être efficacement calculé et stocké dans formulaires à faible densité de données avec l'approche de sparsification de bas rang, qui accélère les MVP dans la solution itérative.

Les processus de l'approche de sparsification de bas rang peuvent être divisés en les étapes suivantes :(1) construire un arbre de cluster en subdivisant l'ensemble de fonctions de base dans chaque sous-domaine, (2) construire un arbre de cluster de blocs par interaction de deux arbres de cluster, ( 3) générer une forme creuse en données de \( {\mathbf{K}}_{rr}^i \) par une condition d'admissibilité, (4) exécuter des algorithmes formatés de bas rang pour obtenir la représentation creuse en données de \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}^{-1} \), et (5) entrez la solution des systèmes FETI-DP en algorithme à faible densité de données. Un préconditionneur approprié peut être utilisé pour accélérer la solution. Il convient de noter que la factorisation LU à faible densité de données \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}={\left({\mathbf {L}}_{rr}^i\right)}_{\mathrm{DS}}{\left({\mathbf{U}}_{rr}^i\right)}_{\mathrm{DS} } \) est adopté pour remplacer l'inversion matricielle \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}^{-1} \). Une technique de dissection emboîtée est utilisée pour améliorer encore l'efficacité de la sparsification de bas rang. La dissection imbriquée utilise des séparateurs pour produire de grands sous-blocs zéro hors diagonale, qui resteront à zéro pendant la factorisation LU afin de réduire considérablement les remplissages.

Pour générer \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}} \), nous construisons d'abord un arbre de cluster T _Je par subdivision récursive de l'ensemble de fonctions de base basé sur les contours de sous-domaine I = {1,2,……N } en utilisant le cadre de délimitation. Avec la dissection imbriquée, un cluster t dans le cadre de délimitation correspondant est divisé en trois successeurs {s ₁ , s _sept. , s ₂ }, où s ₁ et s ₂ sont les ensembles d'index des deux cadres de délimitation et s déconnectés _sept. est l'ensemble d'index du séparateur. La figure 2a montre un exemple simple de ce processus. Ensuite, un arbre de cluster de blocs T _{Je × Je} peut être construit en interagissant deux arbres de cluster T _Je , comme le montre la figure 2 b, qui peut être choisi comme arbre de cluster de l'ensemble de fonctions de base basé sur les bords d'origine et celui de l'ensemble de fonctions de base de test dans la méthode de Galerkin. Ensuite, nous devons introduire une condition d'admissibilité basée sur la dissection imbriquée pour distinguer les blocs complets, les blocs de décomposition de bas rang et les blocs zéro hors diagonale dans T _{Je × Je} [23]. Ainsi, \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}} \) peut être produit en remplissant les blocs correspondants avec les entrées non nulles de \( {\mathbf{K}}_{rr}^i \). Enfin, la factorisation LU de \( {\left({\mathbf{K}}_{rr}^i\right)}_{\mathrm{DS}}={\left({\mathbf{L }}_{rr}^i\right)}_{\mathrm{DS}}{\left({\mathbf{U}}_{rr}^i\right)}_{\mathrm{DS}} \ ) peut être calculé récursivement à partir de

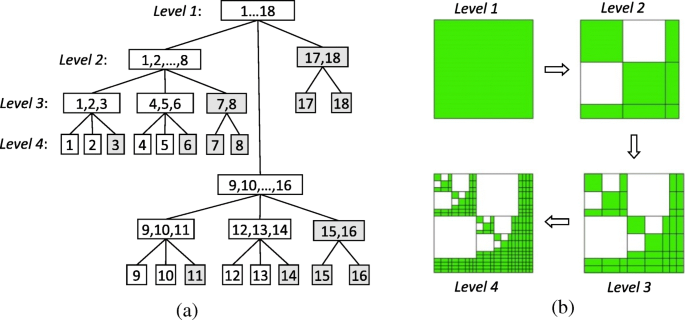
Constructions d'un arbre à clusters et d'un arbre à clusters par blocs de 4 niveaux basés sur la dissection emboîtée. un Construction d'un arbre de cluster par subdivision récursive de l'ensemble de fonctions de base basé sur les bords I = {1,2,…18}. b Construction d'un arbre de cluster de blocs où blanc les blocs sont des matrices nulles et vert les blocs peuvent être des matrices complètes ou des matrices de décomposition de bas rang

où les arithmétiques conventionnelles à matrice complète sont remplacées par leurs homologues à données rares [28]. Une erreur de troncature adaptative ε _t est utilisé pour contrôler la précision des approximations de bas rang. Les facteurs LU obtenus \( {\left({\mathbf{L}}_{rr}^i\right)}_{\mathrm{DS}} \) et \( {\left({\mathbf{U} }_{rr}^i\right)}_{\mathrm{DS}} \) sont stockés et utilisés pour construire \( {\mathbf{Z}}_{rr}^i \) par

où \( {\mathbf{B}}_r^i{\left({\mathbf{U}}_{rr}^i\right)}_{\mathrm{DS}}^{-1} \) et \( {\left({\mathbf{L}}_{rr}^i\right)}_{\mathrm{DS}}^{-1}{\mathbf{B}}_r^i \) peut être calculé par le solveur triangulaire supérieur et inférieur à données éparses. Le \( {\left({\mathbf{L}}_{rr}^i\right)}_{\mathrm{DS}} \), \( {\left({\mathbf{U}}_{ rr}^i\right)}_{\mathrm{DS}} \), et \( {\mathbf{Z}}_{rr}^i \) entrent dans le calcul FETI-DP avec des données éparses en avant et en arrière substitutions (FBS) et MVP à faible densité de données.

Force optique et potentiel

Selon la théorie de l'électrodynamique, la force optique peut être évaluée par le tenseur de contrainte de Maxwell (MST) qui révèle la relation entre le champ électromagnétique et la quantité de mouvement mécanique [29]. Une fois la distribution du champ électromagnétique autour de l'objet obtenue, la force optique peut être calculée en intégrant le MST sur une surface fermée entourant l'objet. Sur la base de la distribution du champ électrique obtenue, le MST à n'importe quelle coordonnée peut être construit par

où l'astérisque en exposant désigne le conjugué du champ électrique ou du champ magnétique, ε sont μ sont la permittivité et la perméabilité, et \( \overleftrightarrow{\mathbf{I}} \) est une matrice identité 3 × 3. Par le produit extérieur des vecteurs, la forme tensorielle de \( \overleftrightarrow{\mathbf{T}} \) peut être écrite comme

où l'indice x , y , z désigne les composants dans trois directions. Selon l'expansion de E décrit en (4), les entrées de MST T _mn (m , n = x , y , z ) peuvent être convertis en formes développées dans le calcul FETI-DP comme

où ω est la fréquence angulaire ; N et s ont été décrits dans l'Eq. (4).

Enfin, la force optique exercée sur l'objet peut être calculée en intégrant le MST sur toute surface fermée qui l'entoure par

A noter que le calcul de la force optique peut également être mis en œuvre en parallèle, puisque l'intégrale du MST est affectée aux sous-domaines correspondants. Pour un piégeage optique stable, l'une des conditions principales est que la force de gradient soit supérieure à la force de diffusion. En d'autres termes, la direction de la force totale doit être identique à celle de la force de gradient, qui pointe toujours vers la position où l'intensité du champ électrique est la plus forte.

Le potentiel optique est un autre paramètre attractif révélant la stabilité du piégeage optique. Sur la base de la force optique obtenue, la profondeur de potentiel optique U à la position r ₀ peut être calculé par

où l'indice ∞ désigne l'infini défini comme le point de référence avec un potentiel nul. La valeur de U peut être représenté par k _B T, où k _B désigne la constante de Boltzmann de 1.3806488 × 10 ⁻²³ J/K et T est la température ambiante. Généralement, la particule peut surmonter le mouvement brownien en solution et être piégée de manière stable lorsque U> 1 k _B T est satisfait. Sinon, la particule ne peut pas être piégée de manière stable. Étant donné que la force optique totale comprend la composante de force de gradient conservatrice et la composante de force de diffusion non conservatrice, la force optique totale F de (15) est non conservateur [30, 31]. Cependant, à condition que le mouvement de la nanoparticule soit limité à une dimension, cela donne une définition sans ambiguïté d'un potentiel optique à partir de (16), même si la force optique totale n'est pas conservatrice.

Résultats et discussion

Trois exemples sont présentés pour démontrer l'efficacité de la méthode proposée. Étant donné que les métaux nobles sont couramment utilisés pour exciter le plasmon de surface, nous sélectionnons des matériaux d'or et d'argent représentatifs pour les analyses. Le premier exemple calcule la force optique d'une nanoparticule d'argent pour vérifier l'exactitude de la méthode proposée. Les deuxième et troisième exemples simulent et discutent le piégeage optique des nanoparticules d'or. Pour tous les exemples, le domaine infini est tronqué avec ABC, et les distances entre l'ABC et les objets sont fixées à une longueur d'onde, ce qui est suffisant pour obtenir une précision acceptable. Tous les calculs sont effectués sur une station de travail Dell équipée de processeurs Intel Xeon à 3,6 GHz.

Nanocapsule d'Argent

Un objet nanocapsule d'argent est d'abord considéré pour tester la précision et l'efficacité de la méthode FETI-DP proposée pour prédire la force optique. La figure 3a et b présente sa configuration et ses dimensions. Les paramètres constitutifs de l'argent sont tous des valeurs mesurées tirées de [32]. Pour mettre en œuvre le schéma FETI-DP, l'ensemble du domaine d'analyse est d'abord divisé en 24 sous-domaines. Des maillages plus denses sont nécessaires près de la surface métallique afin de modéliser l'effet d'amélioration du champ local plasmonique. Des éléments tétraédriques sont adoptés pour la discrétisation, ce qui conduit à un total de 6,9 × 10 ⁵ inconnues, y compris 4.1 × 10 ⁴ inconnues doubles et 313 inconnues de coin. La lumière incidente s'allume dans la direction de +z , tandis que la direction de polarisation du champ électrique est −x .

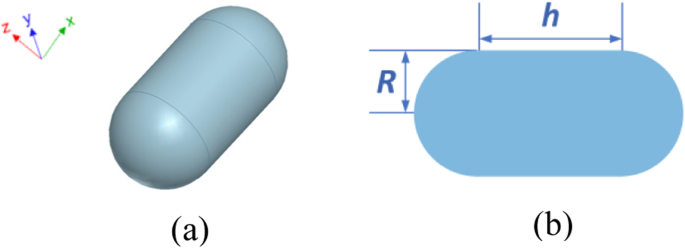
Configuration d'une structure de nanocapsule d'argent. un Vue 3D. b Vue de face et dimensions, où R = 30 nm et h = 60 nm

Tout d'abord, nous modifions la longueur d'onde de la lumière incidente λ de 200 nm à 400 nm pour simuler les forces optiques exercées sur la nanocapsule. Étant donné que le FETI-DP fonctionne dans le domaine fréquentiel, les forces optiques sont calculées à 15 points de fréquence d'échantillonnage. La figure 4 montre la courbe calculée des forces optiques exercées sur la nanocapsule d'argent. Pour indiquer la précision du FETI-DP, les résultats de la force optique du FETI-DP sont comparés à ceux du logiciel commercial Lumerical FDTD Solutions [33], et un bon accord peut être observé.

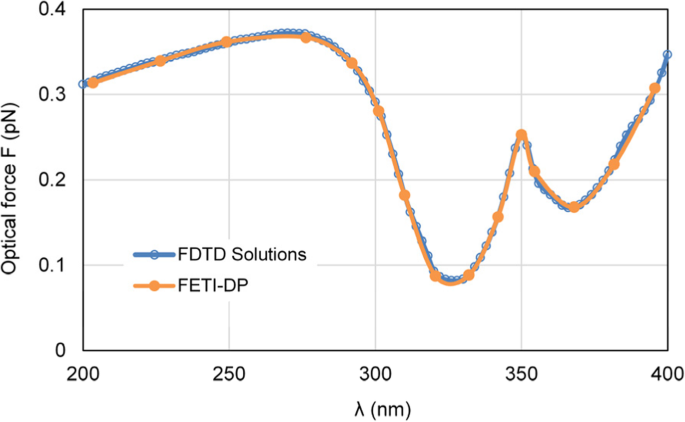
Résultats des forces optiques exercées sur la nanocapsule d'argent, variant avec la longueur d'onde λ de lumière incidente, y compris les résultats du FETI-DP et les solutions logicielles commerciales FDTD

Then, the performance of FETI-DP is tested for different numbers of subdomains. We increase the number of subdomains from 4 to 24 by keeping the discretization density. We assign each processor to deal with one subdomain. Table 1 reports the time used for the construction of global interface Eq. (6) and the total solution time. It can be seen that the FETI-DP can fully exploit parallel computing resources and significantly improve the solution efficiency. Besides, the accuracy of the FETI-DP with the number of subdomains increasing is also examined and reported in Table 1. Here, the accuracy is defined by the 2-norm relative error of the optical force as δ _OF  = ‖OF _i  − OF _ref ‖/‖OF _ref ‖, where OF _i is the optical force using i subdomains and OF _ref denotes the reference optical force using two subdomains. It can be seen that the accuracy keeps almost constant with the number of subdomains increasing.

Gold Nanosphere Dimer

The second example analyzes the optical trapping of a gold nanosphere by using a gold nanosphere dimer. The plasmonic effects at the dimer gap can effectively enhance the optical force for trapping nanoparticle. Figure 5 a and b gives the configuration and dimensions of this system. The constitutive parameters of gold are all measured values taken from [32]. The surrounding medium is water with a relative refractive index of n  = 1.33. The incident light is a plane wave with the power of 10 mW/μm ² , the electric field polarization direction is +x , and the incident direction is −z . The optical force exerted on the object nanosphere is calculated by the FETI-DP method. For the FETI-DP implementation, the whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which results in 3.5 × 10 ⁶ unknowns, including 1.6 × 10 ⁵ dual unknowns and 1738 corner unknowns.

Configuration of an optical trapping system of a gold nansphere dimer in water. un 3D view. b Front view and dimensions, where R = 25 nm, r = 5 nm, and g = 2 nm

First, we test the parallel performance of the proposed FETI-DP by using various numbers of processors. Table 2 reports the solution time for Eq. (6) as well as the total solution time. Besides, the speedups for the parallel computation are also provided in Table 2. Here, the speedup is defined by

where \( {T}_{N_p} \) denotes the total wall-clock time using N _p processors. It can be seen that the FETI-DP significantly improves the solution efficiency and exhibits good parallel speedup. For this large number of unknowns, the total memory usage of all the processors is only 57.2 GB.

Then, the effectiveness of the low-rank sparsification approach is examined. With the low-rank sparsification, the subdomain matrix can be factorized by data-sparse algorithm and stored as data-sparse matrices. The construction time and memory usage are only 18 s and 0.5 GB, while they are 67 s and 1.7 GB by conventional matrix algorithm. It can be seen that we get 72% time saving and 70% memory compression. Related to the memory usage, the subsequent MVPs can also get 70% time-saving.

Next, the FETI-DP is tested for the optical force calculation with the wavelength λ varying from 277 nm to 818 nm. In practice, the analyses of optical force under incident light of different wavelengths are often necessary for searching the plasmonic resonance wavelength, where drastic field enhancement occurs and the strongest optical force can be obtained. Two cases are considered with the nanosphere located at (0, 0, 20 nm) and (0, 0, − 20 nm). Figure 6 a and b plots the calculated optical forces exerted on the nanosphere for different λ . It can be seen that the maximum optical force occurs at λ  = 472 nm, which is the plasmonic resonance wavelength. The optical force at this resonance wavelength enhanced by nearly 40 times as against that at non-resonance wavelength. Moreover, the optical force always points to the dimer gap, as shown in Fig. 6, where the electric field intensity is strongest. It is also the direction of gradient force to trap the object. Figure 7 a and b shows the calculated electric field enhancement distributions at the non-resonance wavelength of λ = 300 nm and the resonance wavelength of λ = 472 nm, respectively. It can be seen that the electric field intensity has been increased by almost 250 times due to the plasmonic resonance effect.

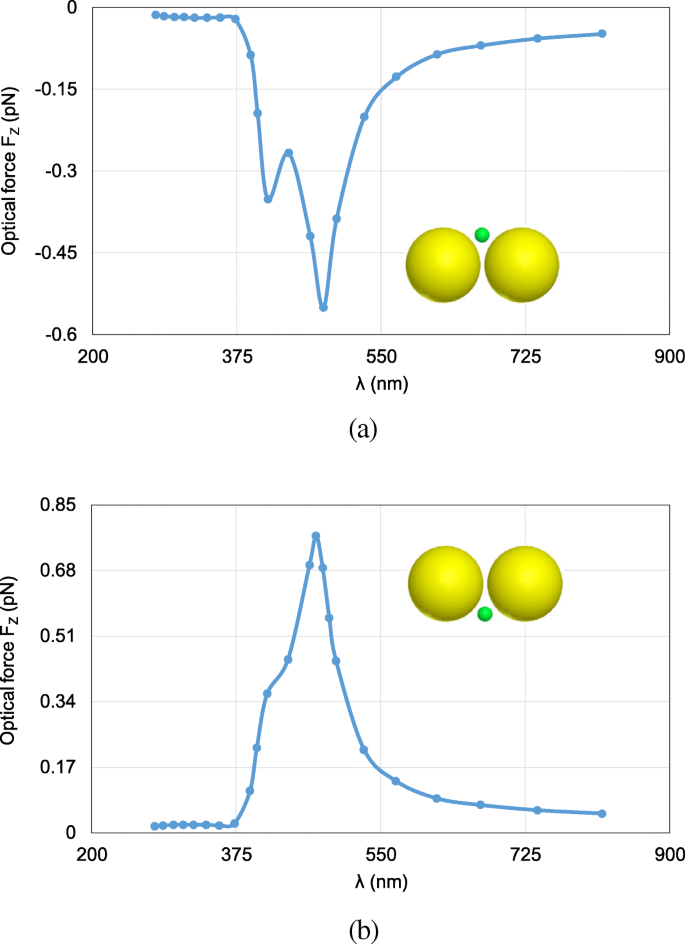
Calculated results of optical forces exerted on the nanosphere in the system of gold nanosphere dimer, varying with the wavelength λ of incident light. un The object nanosphere is located at (0, 0, 20 nm). b The object nanosphere is located at (0, 0, − 20 nm)

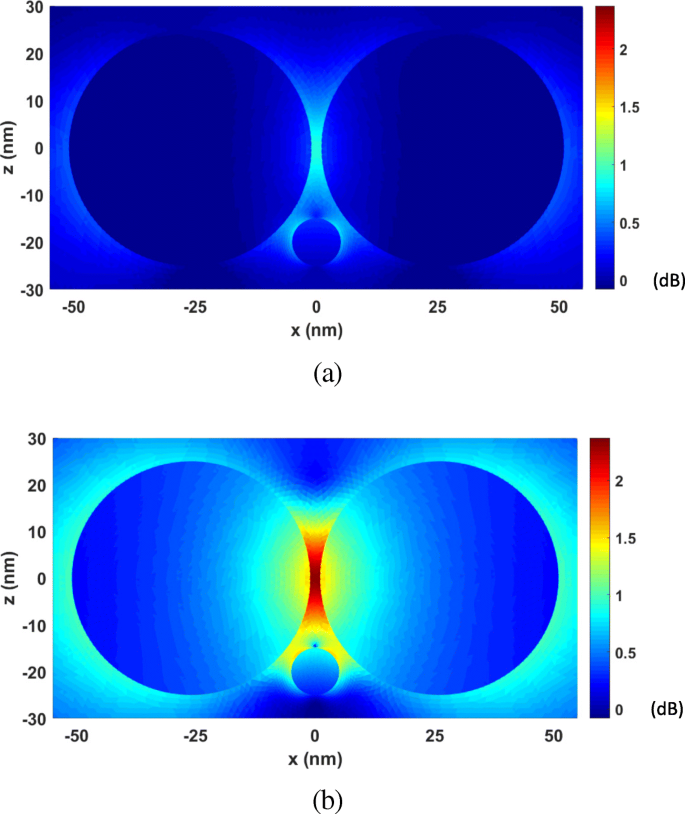
The electric field enhancement distributions on the xoz plane for the system of gold nanosphere dimer. un λ = 300 nm (non-resonance wavelength). b λ  = 472 nm (resonance wavelength)

Besides, the optical force and optical potential are calculated with the nanosphere moving from (0, 0, − 30 nm) to (0, 0, − 17 nm) along the z -axe. Since the most typical and interesting behavior of trapping forces and potentials are those acting along z -direction, we here consider the axial trapping potential by integration along the z -axe. Because the motion of the nanoparticle is restricted to one dimension, the definition of an optical potential is unambiguous from (16), even though the total optical force from (15) is non-conservative. As shown in Fig. 8 a, b, with the nanosphere moving to the dimer gap, the optical force and optical potential depth obviously increase. At the position of (0, 0, − 17 nm), an optical potential depth of 4.6 k _B T is produced, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

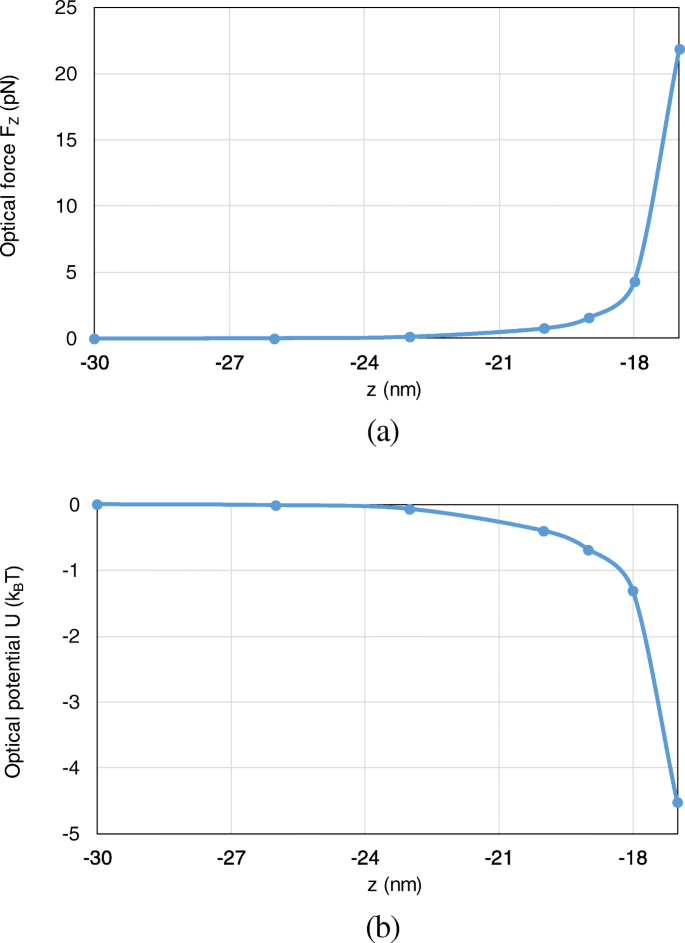
The optical forces and optical potentials exerted on the nanosphere in the system of gold nanosphere dimer, when the nanosphere moves from (0, 0, − 30 nm) to (0, 0, − 17 nm). un The optical forces. b The optical potentials

Finally, we test the effects of the dielectric substrate for this example. The optical forces are calculated with and without a substrate, respectively. For both two cases, the nanosphere is located at (0, 0, − 20 nm) and the incident wavelength is chosen as the resonance wavelength. For the case without substrate, the calculated result of the optical force is |F ₀ | = 0.769 pN. For the case with a substrate, the gold nanosphere dimer is put on a dielectric substrate with a thickness of 60 nm and a relative permittivity of ε _r = 2.25. The calculated result of the optical force is |F ₁ | = 0.761 pN. The relative error between these two results of optical forces is about 1.0 × 10 ⁻² , which is defined as |F ₁  − F ₀ |/|F ₀ |.

Gold Truncated Cone Dimer

The third example deals with the optical trapping of a gold nanosphere by using a gold truncated cone dimer. Figure 9 gives the configuration and dimensions of this system. The constitutive parameters of gold are taken from [32]. The dielectric substrate has a relative permittivity of ε _r  = 2.25. The surrounding medium is water with a relative refractive index of n  = 1.33. The incident light is plane wave with the power of 10 mW/μm ² , the electric field polarization direction is +x , and the incident direction is −z . The whole computational domain is divided into 32 subdomains and discretized by tetrahedral meshes, which leads to 3.1 × 10 ⁶ unknowns, including 1.3 × 10 ⁵ dual unknowns and 1227 corner unknowns.

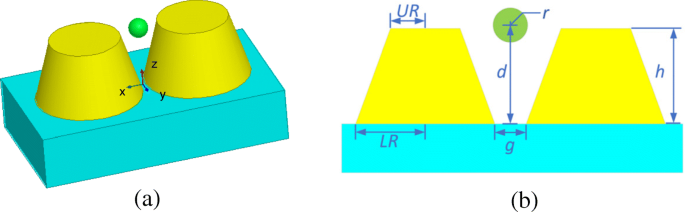
Configuration of an optical trapping system of a gold truncated cone dimer based on a dielectric substrate in water. un 3D view. b Front view and dimensions, where UR = 20 nm, LR = 30 nm, h = 35 nm, and g = 2 nm

First, we analyze the optical forces by changing λ from 277 nm to 818 nm. Figure 10 plots the calculated optical forces exerted on the nanosphere for different λ . The nanosphere is located at (0, 0, 35 nm). It can be seen that the maximum optical force occurs at λ  = 464 nm, which is the plasmonic resonance wavelength, and the optical force here is enhanced by nearly 30 times at non-resonance wavelength. Moreover, the total optical force always points to −z , as shown in Fig. 10, which is the direction of the gradient force. This confirms that the gradient force is greater than the scattering force, which is one of the conditions that the nanosphere can be stably trapped. Figure 11 a and b presents the calculated electric field distributions at the non-resonance wavelength of λ =300 nm and the resonance wavelength of λ = 464 nm, respectively. It can be seen that electric field intensity has been increased by almost 500 times due to the localized surface plasmon resonance.

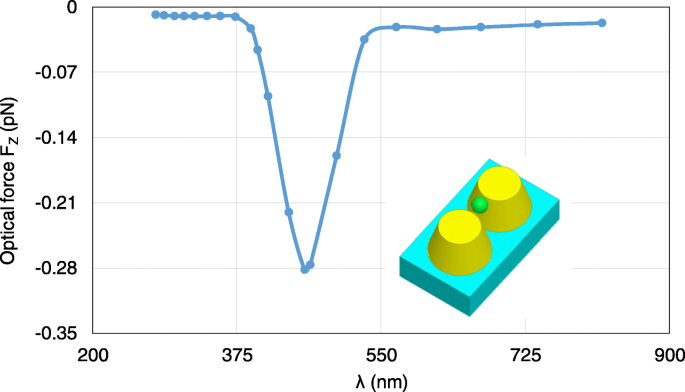
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer, varying with λ . The nanosphere is located at (0, 0, 35 nm)

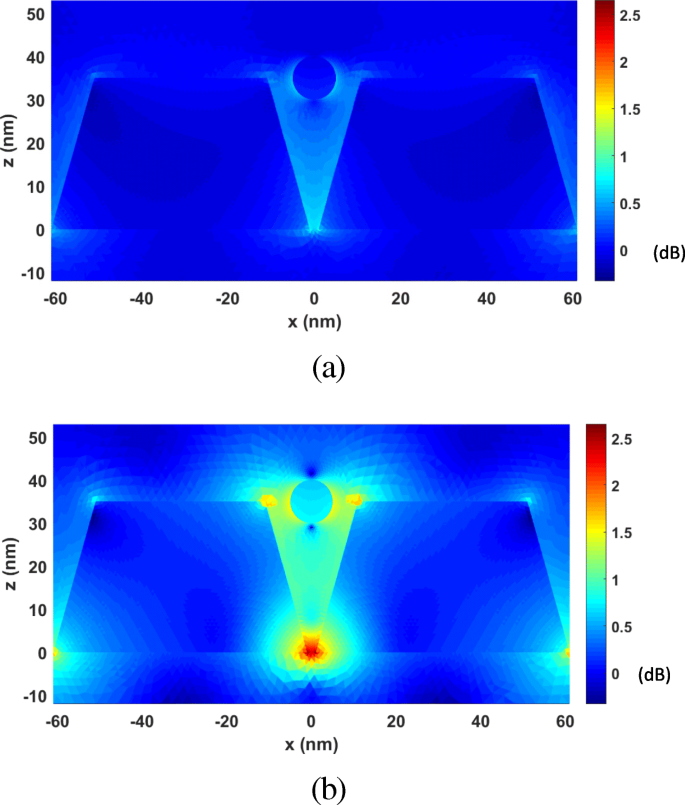
The electric field enhancement distributions on the xoz plane for the system of gold truncated cone dimer. un λ =300 nm (non-resonance wavelength). b λ =464 nm (resonance wavelength)

Then, the location of the nanosphere is changed to 0, 5, and 35 nm to observe the optical force. Figure 12 gives the calculated optical forces exerted on the nanosphere, where obvious y -component of optical force can be observed, while greater z -component of optical force exists. The total optical force still points to the position with the strongest electric field to trap the nanosphere.

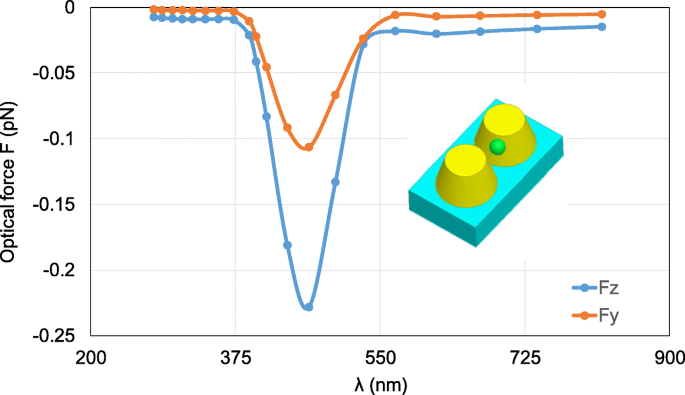
Calculated results of optical forces exerted on the nanosphere in the system of gold truncated cone dimer varying λ . The nanosphere is located at (0, 5 nm, 35 nm)

Furthermore, we analyze the optical potential with the nanosphere moving from (0, 0, 50 nm) to (0, 0, 20 nm) along the z -axe. Here, we consider the axial trapping potential along z -direction, which restricts the motion of the nanoparticle to one dimension and leads to an unambiguous definition of optical potential. Both the optical force and potential are calculated. As can be observed from Fig. 13 a, b, with the nanosphere moving to the dimer gap, the optical force and the optical potential depth obviously increase. At (0, 0, 20 nm), an optical potential depth of 3.8 k _B T is obtained, which is sufficient to overcome the Brownian motion in water to achieve stable optical trapping.

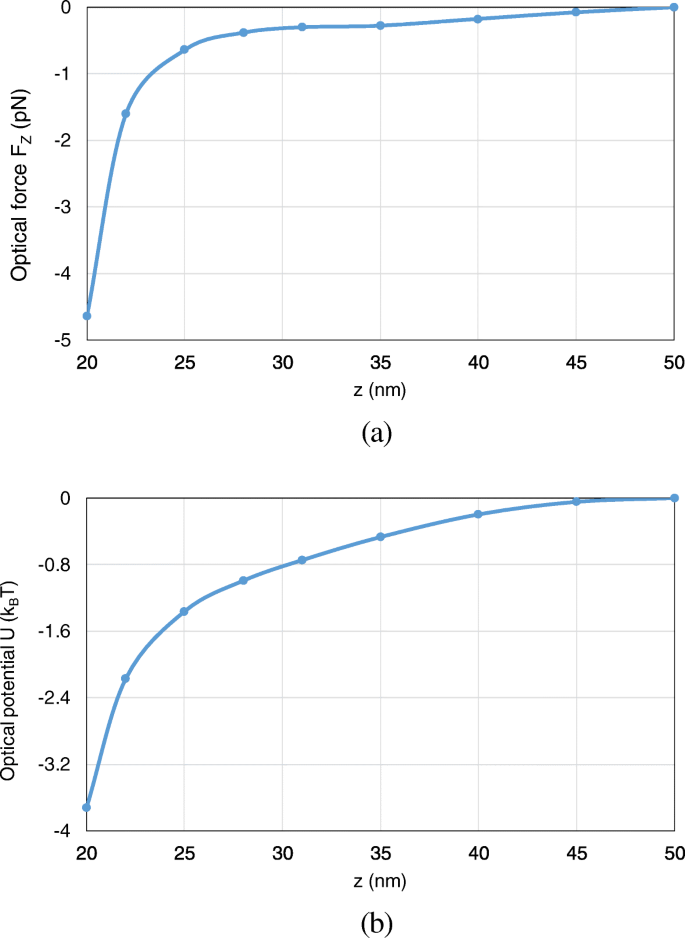
The optical forces and optical potentials exerted on the nanosphere in the system of gold truncated cone dimer, when the nanosphere moves from (0, 0, 50 nm) to (0, 0, 20 nm). un The optical forces. b The optical potentials

Finally, we test the computational costs of the FETI-DP by changing the number of unknowns from 1.0 million to 3.2 million based on different mesh size. In practice, the tests under different mesh density are usually necessary to meet different accuracy requirements. Such a large-scale complex problem brings great challenges to conventional numerical methods. However, the FETI-DP can easily handle this problem. Thirty-two processors are employed for the FETI-DP simulation, while each processor deals with a subdomain. Table 3 reports the computational costs of the FETI-DP. It can be seen that the FETI-DP exhibits high simulation efficiency and low memory requirement.

Conclusion

An FETI-DP method combined with low-rank sparsification is proposed for the prediction and analysis of optical trapping of metal nanoparticles. The proposed method provides fully decoupled subdomain problems, which converts a large-scale complex problem into a series of small-scale simple problems. It is well-suited for parallel computation and can significantly improve the efficiency of numerical simulation. Examples demonstrate that the proposed method exhibits excellent performance of large-scale computation and is well-suited for the fast and accurate simulation of optical trapping at nanoscale.

Disponibilité des données et des matériaux

All data generated or analyzed during this study are included in this article.

Abréviations

ABC:

Absorbing boundary condition

DOF:

Degrees of freedom

FDTD :

Domaine temporel aux différences finies

FEM :

Méthode des éléments finis

FETI-DP:

Dual-primal finite element tearing and interconnecting

MST:

Maxwell stress tensor

MVP:

Matrix-vector product