Méthode et analyse du courant de maillage

La Méthode Mesh-Courant , également connue sous le nom de Loop Current Method , est assez similaire à la méthode du courant de branche en ce sens qu'elle utilise des équations simultanées, la loi de tension de Kirchhoff et la loi d'Ohm pour déterminer les courants inconnus dans un réseau. Elle diffère de la méthode Branch Current en ce sens qu'elle ne pas utilisez la loi actuelle de Kirchhoff, et il est généralement capable de résoudre un circuit avec moins de variables inconnues et moins d'équations simultanées, ce qui est particulièrement agréable si vous êtes obligé de résoudre sans calculatrice.

Mesh Current, méthode conventionnelle

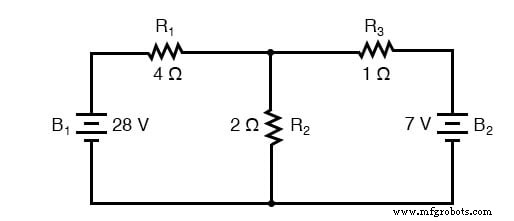
Voyons comment cette méthode fonctionne sur le même exemple de problème :

Identifier les boucles

La première étape de la méthode Mesh Current consiste à identifier les « boucles » dans le circuit englobant tous les composants. Dans notre exemple de circuit, la boucle formée par B₁ , R₁ , et R₂ sera le premier tandis que la boucle formée par B₂ , R₂ , et R₃ sera le deuxième. La partie la plus étrange de la méthode Mesh Current consiste à envisager des courants de circulation dans chacune des boucles. En fait, cette méthode tire son nom de l'idée de ces courants s'engrenant entre des boucles comme des ensembles d'engrenages en rotation :

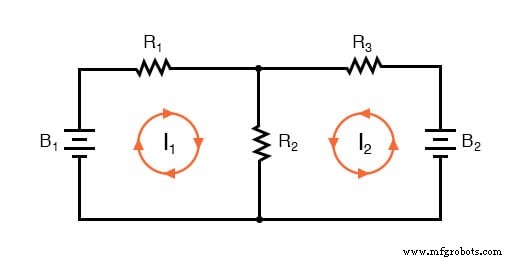
Le choix de la direction de chaque courant est entièrement arbitraire, tout comme dans la méthode Branch Current, mais les équations résultantes sont plus faciles à résoudre si les courants vont dans la même direction à travers des composants d'intersection (notez comment les courants I₁ et moi₂ vont tous les deux « monter » à travers la résistance R₂ , où ils « s'entrecroisent » ou se coupent). Si la direction supposée d'un courant de maille est fausse, la réponse pour ce courant aura une valeur négative.

Étiquetez les polarités de chute de tension

L'étape suivante consiste à étiqueter toutes les polarités de chute de tension à travers les résistances en fonction des directions supposées des courants de maille. N'oubliez pas que l'extrémité "en amont" d'une résistance sera toujours négative et l'extrémité "en aval" d'une résistance positive l'une par rapport à l'autre, car les électrons sont chargés négativement. Les polarités de la batterie, bien sûr, sont dictées par l'orientation de leurs symboles dans le diagramme, et peuvent ou non « concorder » avec les polarités des résistances (sens du courant supposé) :

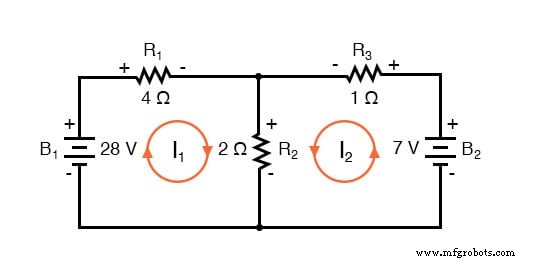
En utilisant la loi de tension de Kirchhoff, nous pouvons maintenant contourner chacune de ces boucles, générant des équations représentatives des chutes de tension et des polarités des composants. Comme pour la méthode du courant de dérivation, nous désignerons la chute de tension d'une résistance comme le produit de la résistance (en ohms) et de son courant de maille respectif (cette quantité étant inconnue à ce stade). Lorsque deux courants s'entremêlent, nous écrirons ce terme dans l'équation avec le courant de résistance étant la somme des deux courants d'engrènement.

Tracer la boucle gauche du circuit avec des équations

Traçage de la boucle gauche du circuit, en partant du coin supérieur gauche et en se déplaçant dans le sens inverse des aiguilles d'une montre (le choix des points de départ et des directions n'a finalement pas d'importance), en comptant la polarité comme si on avait un voltmètre en main, fil rouge sur le point en avant et plomb noir sur la pointe derrière, on obtient cette équation :

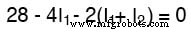
Notez que le terme moyen de l'équation utilise la somme des courants de maille I₁ et moi₂ comme le courant à travers la résistance R₂ . C'est parce que les courants de maille I₁ et moi₂ vont dans la même direction par R₂ , et se complètent ainsi. Distribution du coefficient de 2 au I₁ et moi₂ termes, puis en combinant I₁ termes de l'équation, nous pouvons simplifier ainsi :

À ce stade, nous avons une équation à deux inconnues. Pour pouvoir résoudre deux courants de maille inconnus, nous devons avoir deux équations. Si nous traçons l'autre boucle du circuit, nous pouvons obtenir une autre équation KVL et avoir suffisamment de données pour résoudre les deux courants. Créature d'habitude que je suis, je vais commencer par le coin supérieur gauche de la boucle de droite et tracer dans le sens inverse des aiguilles d'une montre :

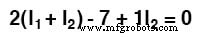
En simplifiant l'équation comme précédemment, nous nous retrouvons avec :

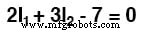
Résoudre l'inconnu

Maintenant, avec deux équations, nous pouvons utiliser l'une des nombreuses méthodes pour résoudre mathématiquement les courants inconnus I₁ et moi₂ :

Retracer le circuit

Sachant que ces solutions sont des valeurs pour mesh courants, pas de branche courants, nous devons revenir à notre schéma pour voir comment ils s'emboîtent pour donner des courants à travers tous les composants :

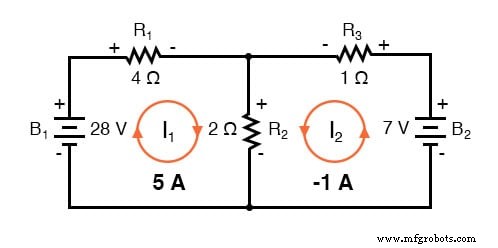
La solution de -1 ampère pour I₂ signifie que nous avons initialement supposé que le sens du courant était incorrect. En réalité, je₂ s'écoule dans le sens inverse des aiguilles d'une montre à une valeur (positive) de 1 amp :

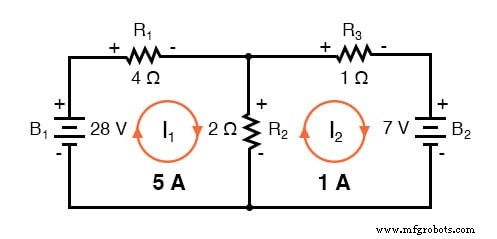
Ce changement de direction du courant par rapport à ce qui était initialement supposé modifiera la polarité des chutes de tension aux bornes de R₂ et R₃ en raison du courant I₂ . A partir de là, on peut dire que le courant passant par R₁ est de 5 ampères, avec la chute de tension aux bornes de R₁ étant le produit du courant et de la résistance (E=IR), 20 volts (positif à gauche et négatif à droite).

Aussi, nous pouvons dire sans risque que le courant à travers R₃ est de 1 amp, avec une chute de tension de 1 volt (E=IR), positive à gauche et négative à droite. Mais que se passe-t-il à R₂ ?

Courant de maille I₁ va « descendre » via R₂ , tandis que le courant de maille I₂ va « monter » via R₂ . Pour déterminer le courant réel via R₂ , il faut voir comment mailler les courants I₁ et moi₂ interagir (dans ce cas, ils sont en opposition), et les additionner algébriquement pour arriver à une valeur finale. Depuis que je₁ est en train de « baisser » à 5 ampères, et je₂ monte à 1 amp, le vrai courant à travers R₂ doit être une valeur de 4 ampères, allant « vers le bas » :

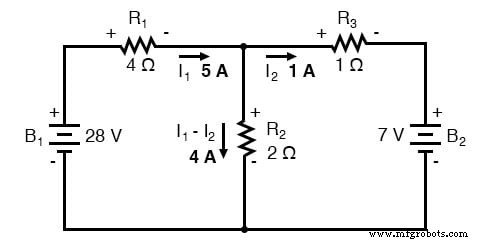
Un courant de 4 ampères à travers R₂ La résistance de 2 Ω nous donne une chute de tension de 8 volts (E=IR), positive en haut et négative en bas.

Avantage de l'analyse du courant de maillage

Le principal avantage de l'analyse Mesh Current est qu'elle permet généralement de résoudre un grand réseau avec moins de valeurs inconnues et moins d'équations simultanées. Notre exemple de problème a pris trois équations pour résoudre la méthode Branch Current et seulement deux équations utilisant la méthode Mesh Current. Cet avantage est d'autant plus grand que les réseaux deviennent de plus en plus complexes :

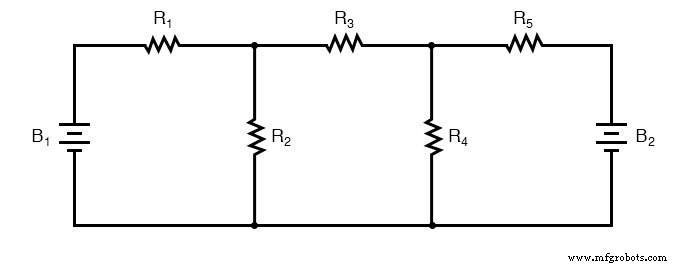
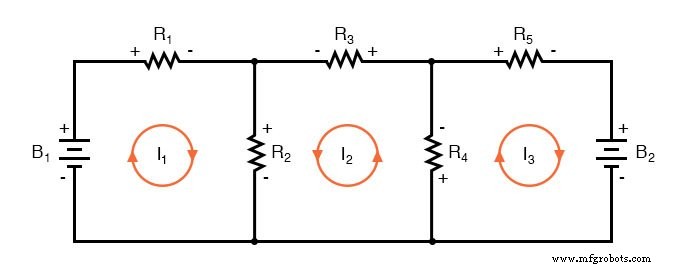
Pour résoudre ce réseau à l'aide de courants de branche, nous devrons établir cinq variables pour tenir compte de chaque courant unique dans le circuit (I₁ par I₅ ). Cela nécessiterait cinq équations pour la solution, sous la forme de deux équations KCL et trois équations KVL (deux équations pour KCL aux nœuds et trois équations pour KVL dans chaque boucle) :

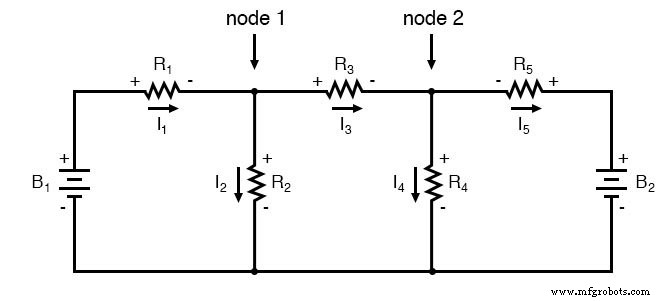
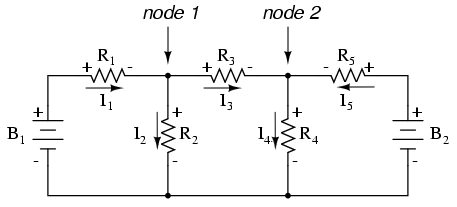
Je suppose que si vous n'avez rien de mieux à faire avec votre temps que de résoudre cinq variables inconnues avec cinq équations, cela ne vous dérangera peut-être pas d'utiliser la méthode d'analyse Branch Current pour ce circuit. Pour ceux d'entre nous qui ont mieux à faire avec notre temps, la méthode Mesh Current est beaucoup plus simple, ne nécessitant que trois inconnues et trois équations à résoudre :

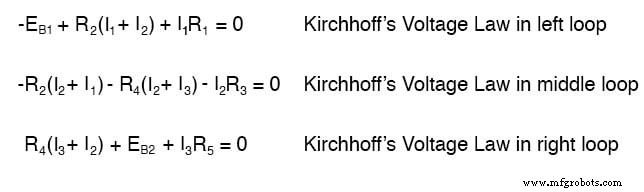
Moins d'équations avec lesquelles travailler est un avantage décisif, en particulier lors de l'exécution d'une résolution d'équation simultanée à la main (sans calculatrice).

Pont de Wheatstone déséquilibré

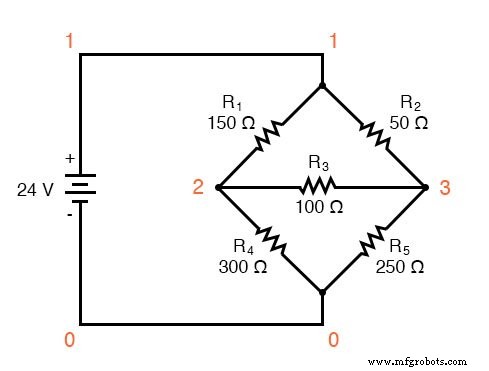
Un autre type de circuit qui se prête bien au Mesh Current est le pont de Wheatstone déséquilibré. Prenons ce circuit, par exemple :

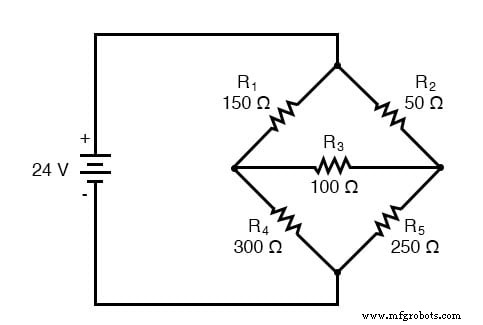
Puisque les rapports de R₁ /R₄ et R₂ /R₅ sont inégaux, on sait qu'il y aura la tension aux bornes de la résistance R₃ , et une certaine quantité de courant à travers elle. Comme indiqué au début de ce chapitre, ce type de circuit est irréductible par une analyse série-parallèle normale et ne peut être analysé que par une autre méthode.

Nous pourrions appliquer la méthode Branch Current à ce circuit, mais cela nécessiterait six courants (I₁ par I₆ ), conduisant à un très grand nombre d'équations simultanées à résoudre. En utilisant la méthode Mesh Current, cependant, nous pouvons résoudre tous les courants et tensions avec beaucoup moins de variables.

Dessiner un maillage

La première étape de la méthode du courant de maillage consiste à tirer juste assez de courants de maillage pour tenir compte de tous les composants du circuit. En regardant notre circuit en pont, il devrait être évident où placer deux de ces courants :

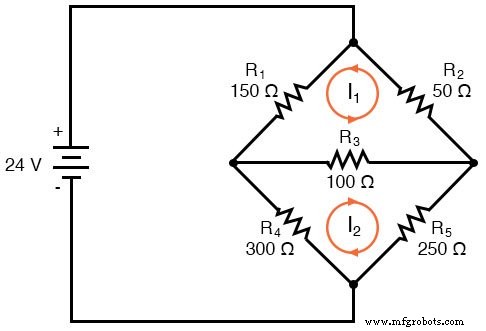
Les directions de ces courants de maille, bien sûr, sont arbitraires. Cependant, deux courants de maille ne suffisent pas dans ce circuit, car ni I₁ ni moi₂ passe par la batterie. Il faut donc ajouter un troisième maillage courant, I₃ :

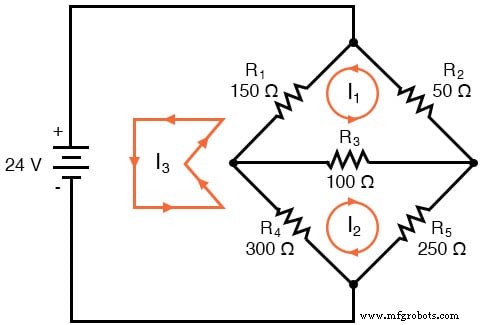
Ici, j'ai choisi I₃ pour boucler du côté inférieur de la batterie, à travers R₄ , via R₁ , et revenez sur le dessus de la batterie. Ce n'est pas le seul chemin que j'aurais pu choisir pour I₃ , mais cela semble le plus simple.

Étiqueter les polarités de chute de tension de la résistance

Maintenant, nous devons étiqueter les polarités de chute de tension de résistance, en suivant chacune des directions supposées des courants :

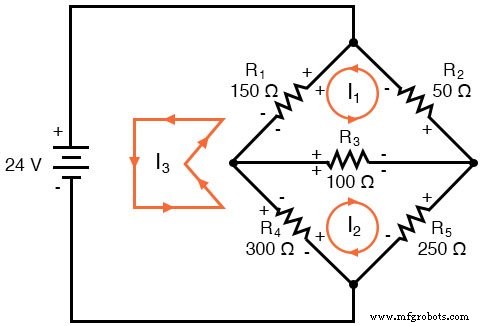
Remarquez quelque chose de très important ici :à la résistance R₄ , les polarités des courants de maille respectifs ne concordent pas. C'est parce que ces courants de maille (I₂ et moi₃ ) passent par R₄ dans des directions différentes. Cela n'empêche pas l'utilisation de la méthode d'analyse Mesh Current, mais cela la complique un peu. Bien que plus tard, nous montrerons comment éviter le R₄ affrontement actuel. (Voir l'exemple ci-dessous)

Utiliser KVL

Génération d'une équation KVL pour la boucle supérieure du pont, en partant du nœud supérieur et en traçant dans le sens des aiguilles d'une montre :

Dans cette équation, nous représentons les directions communes des courants par leurs sommes par des résistances communes. Par exemple, la résistance R₃ , avec une valeur de 100 , a sa chute de tension représentée dans l'équation KVL ci-dessus par l'expression 100(I₁ + I₂ ), puisque les deux courants I₁ et moi₂ passer par R₃ de droite à gauche. La même chose peut être dite pour la résistance R₁ , avec son expression de chute de tension indiquée par 150(I₁ + I₃ ), puisque I₁ et moi₃ passer de bas en haut à travers cette résistance, et ainsi travailler ensemble pour générer sa chute de tension.

Générer une équation KVL pour la boucle inférieure du pont ne sera pas si facile car nous avons deux courants allant l'un contre l'autre à travers la résistance R₄ . Voici comment je procède (en commençant par le nœud de droite et en suivant dans le sens inverse des aiguilles d'une montre) :

Notez comment le deuxième terme de la forme originale de l'équation a la résistance R₄ valeur de 300  multipliée par la différence entre I₂ et moi₃ (Je₂ - Je₃ ). C'est ainsi que nous représentons l'effet combiné de deux courants de maille passant dans des directions opposées à travers le même composant. Le choix des signes mathématiques appropriés est ici très important :300(I₂ - Je₃ ) ne signifie pas la même chose que 300(I₃ - Je₂ ). J'ai choisi d'écrire 300(I₂ - Je₃ ) parce que je pensais d'abord à I₂ effet de (création d'une chute de tension positive, mesure avec un voltmètre imaginaire aux bornes de R₄ , fil rouge en bas et fil noir en haut), et accessoirement de I₃ effet (créant une chute de tension négative, fil rouge en bas et fil noir en haut). Si j'avais pensé en termes de I₃ 's effet d'abord et I₂ effet secondaire, en tenant mes fils de voltmètre imaginaires dans les mêmes positions (rouge en bas et noir en haut), l'expression aurait été -300(I₃ - Je₂ ). Notez que cette expression est mathématiquement équivalent au premier :+300(I₂ - Je₃ ).

Eh bien, cela prend en charge deux équations, mais j'ai toujours besoin d'une troisième équation pour compléter mon ensemble d'équations simultanées de trois variables, trois équations. Cette troisième équation doit également inclure la tension de la batterie, qui jusqu'à présent n'apparaît dans aucune des deux équations KVL précédentes. Pour générer cette équation, je tracerai à nouveau une boucle avec mon voltmètre imaginaire à partir de la borne inférieure (négative) de la batterie, dans le sens des aiguilles d'une montre (encore une fois, la direction dans laquelle je marche est arbitraire et n'a pas besoin d'être la même que la direction du courant de maille dans cette boucle) :

Résoudre les courants

Résolution de I₁ , je₂ , et moi₃ en utilisant la méthode d'équation simultanée que nous préférons :

Exemple : Utilisez Octave pour trouver la solution pour I₁ , je₂ , et moi₃ à partir de la forme simplifiée des équations ci-dessus.

Solution : Dans Octave, un clone Matlab® open source, entrez les coefficients dans la matrice A entre crochets avec les éléments de colonne séparés par des virgules et les lignes séparées par des points-virgules. Entrez les tensions dans le vecteur colonne :b. Les courants inconnus :I₁ , ₂ , et moi₃ sont calculés par la commande :x=A\b. Ceux-ci sont contenus dans le vecteur colonne x.

octave:1>A =[300,100,150;100,650,-300;-150,300,-450] A =300 100 150 100 650 -300 -150 300 -450 octave:2> b =[0;0;-24] b =0 0 -24 octave:3> x =A\b x =-0,093793 0,077241 0,136092

La valeur négative obtenue pour I₁ nous dit que la direction supposée de ce courant de maille était incorrecte. Ainsi, les valeurs de courant réelles à travers chaque résistance sont les suivantes :

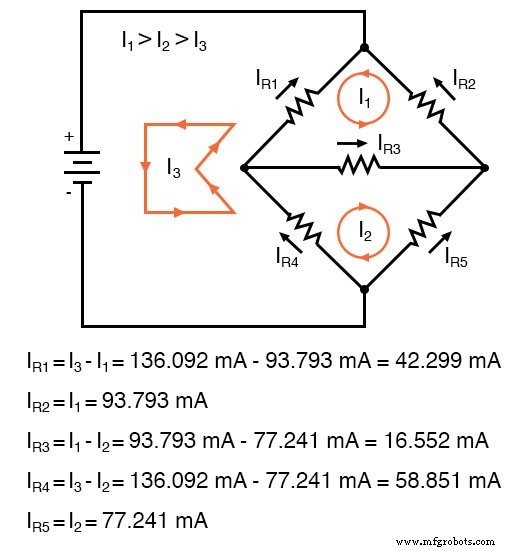
Calcul des chutes de tension sur chaque résistance :

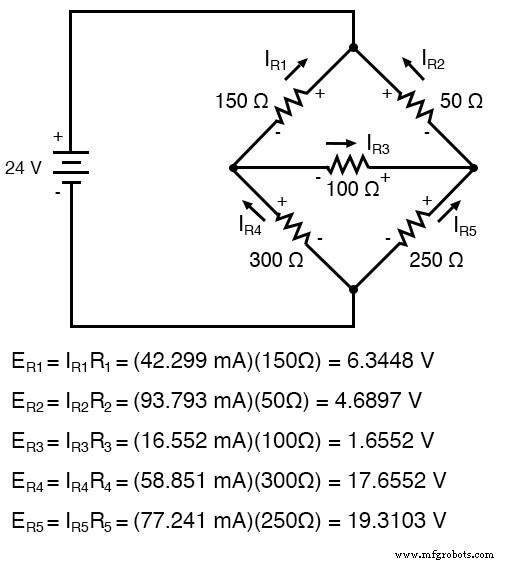
Une simulation SPICE confirme la précision de nos calculs de tension :

pont de Wheatstone déséquilibré v1 1 0 r1 1 2 150 r2 1 3 50 r3 2 3 100 r4 2 0 300 r5 3 0 250 .dc v1 24 24 1 .print dc v(1,2) v(1,3) v(3,2) v(2,0) v(3,0) .finir v1 v(1,2) v(1,3) v(3,2) v(2) v(3) 2.400E+01 6.345E+00 4.690E+00 1.655E+00 1.766E+01 1.931E+01

Exemple :

(a) Trouver un nouveau chemin pour le courant I₃ qui ne produit de polarité contradictoire sur aucune résistance par rapport à I₁ ou I₂ . R₄ était l'élément incriminé. (b) Trouvez des valeurs pour I₁ , je₂ , et moi₃ . (c) Trouvez les cinq courants de résistance et comparez-les aux valeurs précédentes.

Solution :

(a) Route I₃ à R₅ , R_3, et R₁ comme indiqué :

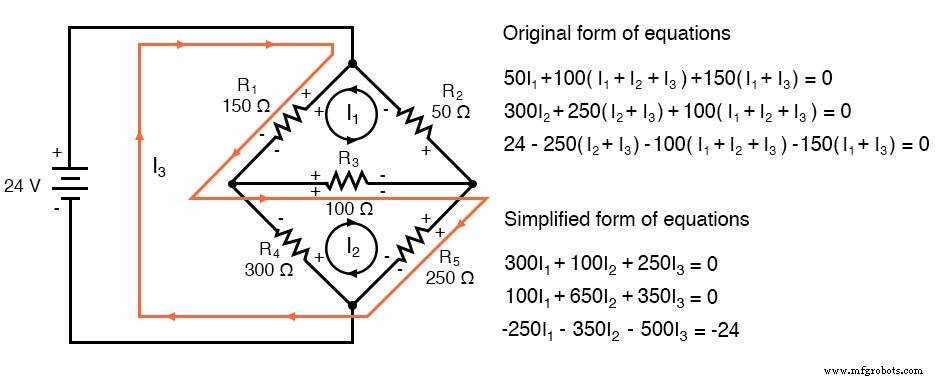
Notez que la polarité contradictoire sur R₄ a été retiré. De plus, aucune des autres résistances n'a de polarités contradictoires.

(b) Octave, un clone Matlab open source (gratuit), donne un vecteur de courant de maillage à « x » :

octave:1> A =[300,100,250;100,650,350;-250,-350,-500] A =300 100 250 100 650 350 -250 -350 -500 octave:2> b =[0;0;-24] b =0 0 -24 octave:3> x =A\b x =-0,093793 -0.058851 0,136092

Pas tous les courants I₁ , je₂ , et moi₃ sont les mêmes (I₂ ) comme le pont précédent en raison de chemins de boucle différents Cependant, les courants de résistance se comparent aux valeurs précédentes :

IR1 =I1 + I3 =-93,793 ma + 136,092 ma =42,299 ma IR2 =I1 =-93,793 mA IR3 =I1 + I2 + I3 =-93,793 ma -58,851 ma + 136,092 ma =-16,552 ma IR4 =I2 =-58,851 mA IR5 =I2 + I3 =-58,851 ma + 136,092 ma =77,241 ma

Étant donné que les courants de résistance sont les mêmes que les valeurs précédentes, les tensions de résistance seront identiques et n'auront pas besoin d'être recalculées.

AVIS :

• Étapes à suivre pour la méthode d'analyse « Mesh Current » :
• (1) Dessinez des courants de maille dans les boucles du circuit, suffisamment pour prendre en compte tous les composants.
• (2) Étiqueter les polarités de chute de tension de résistance en fonction des directions supposées des courants de maille.
• (3) Écrivez les équations KVL pour chaque boucle du circuit, en substituant le produit IR à E dans chaque terme de résistance de l'équation. Lorsque deux courants de maille se croisent à travers un composant, exprimez le courant comme la somme algébrique de ces deux courants de maille (c'est-à-dire I₁ + I₂ ) si les courants vont dans le même sens à travers ce composant. Sinon, exprimez le courant à partir de la différence (c'est-à-dire I₁ - Je₂ ).
• (4) Résoudre les courants de maille inconnus (équations simultanées).
• (5) Si une solution est négative, alors la direction du courant supposée est fausse !
• (6) Ajoutez algébriquement des courants de maille pour trouver des composants de courant partageant plusieurs courants de maille.
• (7) Résoudre les chutes de tension sur toutes les résistances (E=IR).

Courant de maillage par inspection

Nous examinons à nouveau la "méthode du courant maillé" avec tous les courants fonctionnant dans le sens des aiguilles d'une montre (cw). La motivation est de simplifier l'écriture des équations de maillage en ignorant la polarité de la chute de tension de la résistance. Cependant, nous devons faire attention à la polarité des sources de tension par rapport à la direction du courant supposée. Le signe des chutes de tension de la résistance suivra un schéma fixe.

Si nous écrivons un ensemble d'équations de courant de maille conventionnelles pour le circuit ci-dessous, où nous prêtons attention aux signes de la chute de tension à travers les résistances, nous pouvons réorganiser les coefficients dans un modèle fixe :

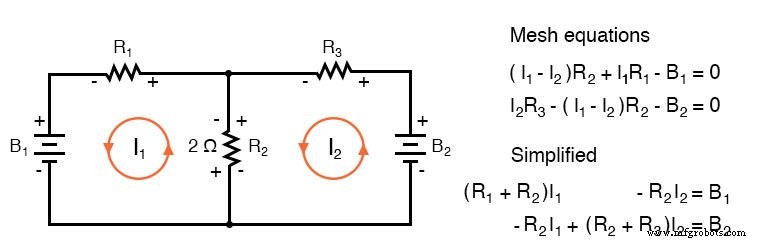
Une fois réarrangé, nous pouvons écrire des équations par inspection. Les signes des coefficients suivent un modèle fixe dans la paire ci-dessus ou l'ensemble de trois dans les règles ci-dessous.

Règles actuelles de maillage :

• Cette méthode suppose des sources de tension de flux de courant conventionnelles. Remplacez toute source de courant en parallèle par une résistance par une source de tension équivalente en série avec une résistance équivalente.
• En ignorant le sens du courant ou la polarité de la tension sur les résistances, tracez des boucles de courant dans le sens inverse des aiguilles d'une montre traversant tous les composants. Évitez les boucles imbriquées.
• Écrire des équations de loi de tension en termes de courants inconnus :I₁ , je₂ , et moi₃ . Le coefficient 1 de l'équation 1, l'équation 2, le coefficient 2 et le coefficient 3 de l'équation 3 sont les sommes positives des résistances autour des boucles respectives.
• Tous les autres coefficients sont négatifs, représentatifs de la résistance commune à une paire de boucles. Le coefficient 2 de l'équation 1 est la résistance commune aux boucles 1 et 2, le coefficient 3 la résistance commune aux boucles 1 et 3. Répétez l'opération pour les autres équations et coefficients.
• +(somme de la boucle R de 1)I1 - (boucle R commune 1-2)I2 - (boucle R commune 1-3)I3 =E1
  -(boucle R commune 1-2)I1 + ( somme de la boucle de R 2)I2 - (boucle R commune 2-3)I3 =E2
  -(boucle R commune 1-3)I1 - (boucle R commune 2-3)I2 + (somme de la boucle 3 de R )I3 =E3
• Le côté droit des équations est égal à une source de tension de flux de courant électronique. Une élévation de tension par rapport au courant supposé dans le sens inverse des aiguilles d'une montre est positive et 0 pour aucune source de tension.
• Résoudre les équations des courants de maille :I₁ , je₂ , et I3. Résolvez les courants à travers des résistances individuelles avec KCL. Résolvez les tensions avec la loi d'Ohm et le KVL.

Bien que les règles ci-dessus soient spécifiques à un circuit à trois mailles, les règles peuvent être étendues à des mailles plus petites ou plus grandes. La figure ci-dessous illustre l'application des règles. Les trois courants sont tous tirés dans le même sens, dans le sens des aiguilles d'une montre. Une équation KVL est écrite pour chacune des trois boucles. Notez qu'il n'y a pas de polarité dessinée sur les résistances. Nous n'en avons pas besoin pour déterminer les signes des coefficients. Cependant, nous devons faire attention à la polarité de la source de tension par rapport au sens du courant. Le I₃ le courant dans le sens horaire sort de la borne positive (+) de la source l24V puis revient à la borne (-). Il s'agit d'une élévation de tension pour le flux de courant conventionnel. Par conséquent, la troisième équation à droite est -24V.

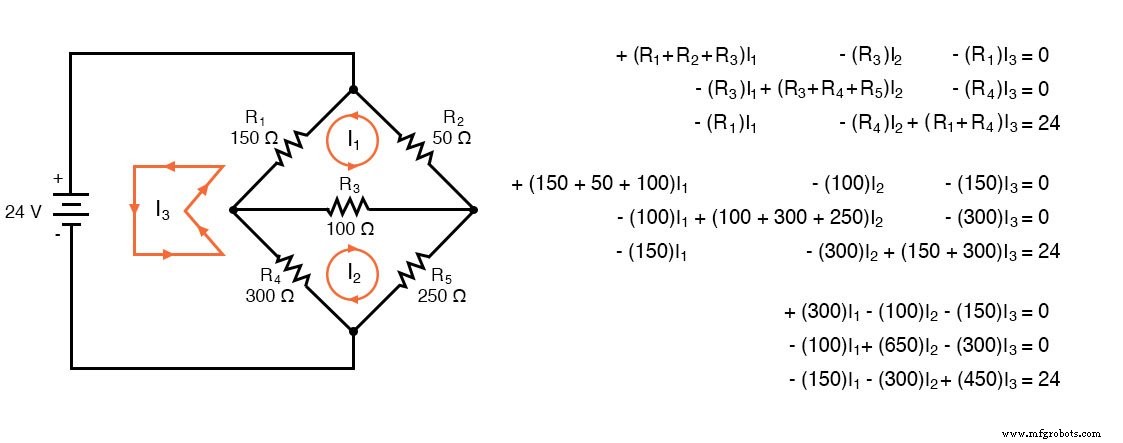
Dans Octave, entrez les coefficients dans la matrice A avec les éléments de colonne séparés par des virgules et les lignes séparées par des points-virgules. Entrez les tensions dans le vecteur colonne b. Résoudre les courants inconnus :I₁ , je₂ , et moi₃ avec la commande :x=A\b. Ces courants sont contenus dans le vecteur colonne x. Les valeurs positives indiquent que les trois courants de maille circulent tous dans le sens supposé des aiguilles d'une montre.

octave:2> A=[300,-100,-150;-100,650,-300;-150,-300,450] A =300 -100 -150 -100 650 -300 -150 -300 450 octave:3> b=[0;0;24] b =0 0 24 octave:4> x=A\b x =0,093793 0,077241 0,136092

Les courants de maille correspondent à la solution précédente par une méthode de courant de maille différente. Le calcul des tensions et courants des résistances sera identique à la solution précédente. Inutile de répéter ici.

Notez que les textes de génie électrique sont basés sur le flux de courant conventionnel. La méthode loop-current, mesh-current dans ces textes exécutera les courants de maille supposés dans le sens des aiguilles d'une montre . Le courant conventionnel sort de la borne (+) de la batterie à travers le circuit, retournant à la borne (-). Une élévation de courant-tension conventionnelle correspond au traçage du courant supposé de (-) à (+) à travers toutes les sources de tension.

Un autre exemple d'un circuit précédent suit. La résistance autour de la boucle 1 est de 6 , autour de la boucle 2 :3 Ω. La résistance commune aux deux boucles est de 2 . Notez les coefficients de I₁ et moi₂ dans la paire d'équations. Tracé du courant supposé de la boucle 1 dans le sens des aiguilles d'une montre à travers B₁ de (+) à (-) correspond à une élévation de tension de flux de courant d'électrons.

Ainsi, le signe du 28 V est positif. La boucle 2 dans le sens antihoraire suppose des traces de courant (-) à (+) via B₂ , une chute de tension. Ainsi, le signe de B₂ est négatif, -7 dans la 2e équation du maillage. Encore une fois, il n'y a pas de marquage de polarité sur les résistances. Ils ne figurent pas non plus dans les équations.

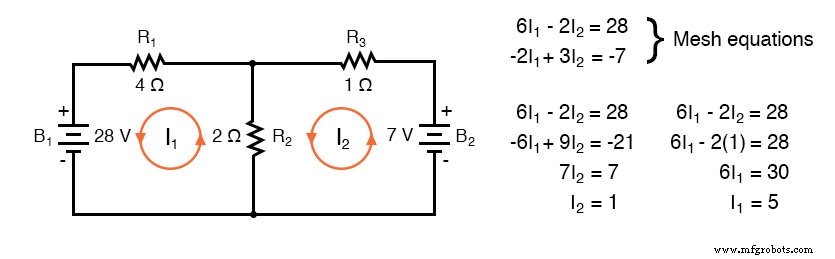
Les courants I₁ =5 A, et I₂ =1 A sont tous les deux positifs. Ils s'écoulent tous les deux dans le sens des boucles dans le sens des aiguilles d'une montre. Cela se compare aux résultats précédents.

Résumé :

• La méthode modifiée du courant de maille évite d'avoir à déterminer les signes des coefficients de l'équation en dessinant tous les courants de maille dans le sens des aiguilles d'une montre pour le flux de courant conventionnel.
• Cependant, nous devons déterminer le signe de toute source de tension dans la boucle. La source de tension est positive si le courant ccw supposé circule avec la batterie (source). Le signe est négatif si le courant ccw supposé circule contre la batterie.
• Voir les règles ci-dessus pour plus de détails.

FICHE DE TRAVAIL CONNEXE :

• Feuille de travail d'analyse du courant de maillage DC

Méthode actuelle de la branche Méthode de tension de nœud