Méthode de tension de nœud
La méthode d'analyse de la tension des nœuds résout les tensions inconnues aux nœuds du circuit en termes d'un système d'équations KCL. Cette analyse semble étrange car elle consiste à remplacer les sources de tension par des sources de courant équivalentes. De plus, les valeurs de résistance en ohms sont remplacées par des conductances équivalentes en siemens, G =1/R. Le siemens (S) est l'unité de conductance, ayant remplacé l'unité mho. Dans tous les cas S =-1. Et S =mho (obsolète).
Méthode de calcul de la tension de nœud
Nous commençons avec un circuit ayant des sources de tension conventionnelles. Un nœud commun E0 est choisi comme point de référence. Les tensions de nœud E1 et E2 sont calculés par rapport à ce point.
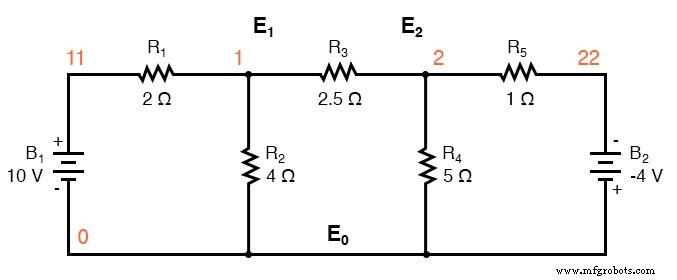
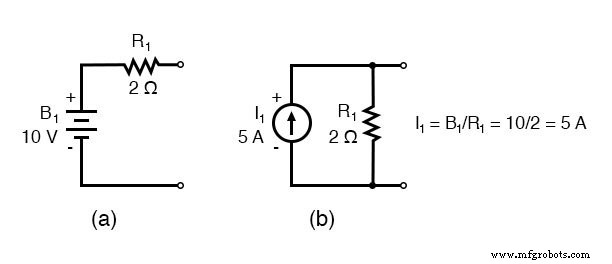
Le remplacement des sources de tension et des résistances en série associées par des sources de courant équivalentes et des résistances parallèles donne le circuit modifié. Remplacez les conductances de résistance en Siemens par la résistance en ohms.
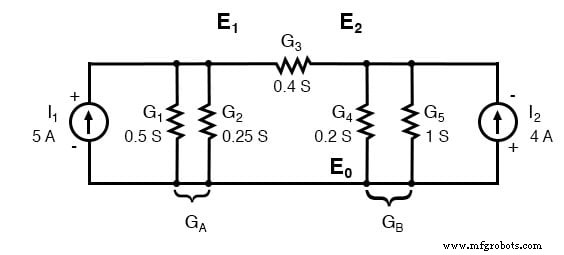
Les conductances parallèles (résistances) peuvent être combinées par addition des conductances. Cependant, nous ne redessinerons pas le circuit. Le circuit est prêt pour l'application de la méthode de tension de nœud.
En dérivant une méthode générale de tension de nœud, nous écrivons une paire d'équations KCL en termes de tensions de nœud inconnues V1 et V2 cette fois. Nous faisons cela pour illustrer un modèle d'écriture d'équations par inspection.
Les coefficients de la dernière paire d'équations ci-dessus ont été réarrangés pour montrer un modèle. La somme des conductances connectées au premier nœud est le coefficient positif de la première tension dans l'équation (1). La somme des conductances connectées au deuxième nœud est le coefficient positif de la deuxième tension dans l'équation (2). Les autres coefficients sont négatifs, représentant les conductances entre les nœuds. Pour les deux équations, le côté droit est égal à la source de courant respective connectée au nœud. Ce modèle nous permet d'écrire rapidement les équations par inspection. Cela conduit à un ensemble de règles pour la méthode d'analyse de la tension de nœud.
Règles de tension de nœud :
- Convertir les sources de tension en série avec une résistance en une source de courant équivalente avec la résistance en parallèle.
- Modifiez les valeurs de résistance en conductances.
- Sélectionnez un nœud de référence (E0 )
- Attribuer des tensions inconnues (E1 )(E2 ) ... (EN ) aux nœuds restants.
- Écrivez une équation KCL pour chaque nœud 1,2, ... N. Le coefficient positif de la première tension dans la première équation est la somme des conductances connectées au nœud. Le coefficient de la deuxième tension dans la deuxième équation est la somme des conductances connectées à ce nœud. Répétez l'opération pour le coefficient de la troisième tension, la troisième équation et d'autres équations. Ces coefficients tombent sur une diagonale.
- Tous les autres coefficients de toutes les équations sont négatifs, représentant les conductances entre les nœuds. La première équation, le deuxième coefficient est la conductance du nœud 1 au nœud 2, le troisième coefficient est la conductance du nœud 1 au nœud 3. Remplissez les coefficients négatifs pour les autres équations.
- Le côté droit des équations est la source de courant connectée aux nœuds respectifs.
- Résoudre le système d'équations pour les tensions de nœud inconnues.
Exemple de méthode de tension de nœud
Exemple : Configurez les équations et résolvez les tensions des nœuds à l'aide des valeurs numériques de la figure ci-dessus.
Solution :
La résolution de deux équations peut être effectuée avec une calculatrice, ou avec une octave (non représentée). La solution est vérifiée avec SPICE sur la base du schéma de principe original avec des sources de tension. Cependant, le circuit avec les sources de courant aurait pu être simulé.
Encore un exemple. Celui-ci a trois nœuds. Nous n'énumérons pas les conductances sur le schéma de principe. Cependant, G1 =1/R1 , etc.
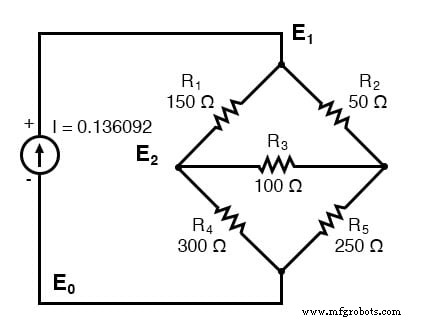
Il y a trois nœuds pour lesquels écrire des équations par inspection. Notez que les coefficients sont positifs pour l'équation (1) E1 , équation (2) E2 , et l'équation (3) E3 . Ce sont les sommes de toutes les conductances connectées aux nœuds. Tous les autres coefficients sont négatifs, représentant une conductance entre les nœuds. Le côté droit des équations est la source de courant associée, 0,136092 A pour la seule source de courant au nœud 1. Les autres équations sont nulles du côté droit pour un manque de sources de courant. Nous sommes trop paresseux pour calculer les conductances des résistances sur le schéma. Ainsi, les G indicés sont les coefficients.
Nous sommes tellement paresseux que nous entrons des résistances réciproques et des sommes de résistances réciproques dans la matrice d'octave "A", laissant octave calculer la matrice de conductances après "A=". La ligne d'entrée initiale était si longue qu'elle était divisée en trois rangées. Ceci est différent des exemples précédents. La matrice « A » entrée est délimitée par des crochets de début et de fin. Les éléments de colonne sont séparés par des espaces. Les lignes sont séparées par une « nouvelle ligne ». Les virgules et les points-virgules ne sont pas nécessaires comme séparateurs. Cependant, le vecteur courant à "b" est séparé par des points-virgules pour donner un vecteur colonne de courants.
Notez que les coefficients diagonaux de la matrice « A » sont positifs, que tous les autres coefficients sont négatifs.
La solution en tant que vecteur de tension est en « x ». E1 =24.000 V, E2 =17,655 V, E3 =19,310 V. Ces trois tensions se comparent au courant de maille précédent et aux solutions SPICE au problème de pont déséquilibré. Ce n'est pas une coïncidence, car la source de courant 0,13609 A a été volontairement choisie pour produire le 24 V utilisé comme source de tension dans ce problème.
Résumé
- Compte tenu d'un réseau de conductances et de sources de courant, la méthode d'analyse de circuit de tension de nœud résout les tensions de nœud inconnues à partir des équations KCL.
- Voir les règles ci-dessus pour plus de détails sur la rédaction des équations par inspection.
- L'unité de conductance G est le siemens S. La conductance est l'inverse de la résistance :G =1/R
FICHES DE TRAVAIL CONNEXES :
- Fiche de travail sur les circuits de diodes précises
- Feuille de travail sur les lois de Kirchhoff
Technologie industrielle



