Mouvement et inclinaison du mur de domaine induits par le courant dans les hippodromes magnétisés perpendiculairement

Contexte

Le mouvement de la paroi du domaine magnétique induit par le courant (CIDWM) dans les hippodromes a révélé un nouveau dispositif de mémoire magnétique pour hippodrome [1, 2]. En raison de cette perspective prometteuse, de nombreux travaux ont été menés au cours des dernières décennies. Le CIDWM a d'abord été étudié dans des ferroaimants (FM) avec une anisotropie magnétique dans le plan et le couple de transfert de spin (STT) généré par le courant polarisé en spin agit comme force motrice [3, 4]. Par la suite, CIDWM a également été réalisé dans des FMs avec anisotropie magnétique perpendiculaire (PMA) [5, 6]. Cependant, dans certains matériaux PMA, la direction du mouvement de la paroi du domaine (DW) est opposée à la direction du flux d'électrons, ce qui est contradictoire avec la prédiction de STT [7, 8]. Et bien d'autres travaux montrent que le mouvement DW se fait dans la direction du courant dans les structures bicouches en métaux lourds (HM)/FM avec PMA. Il a été démontré que les couples spin-orbite (SOT) générés par HM par effet Hall de spin et/ou effet Rashba ainsi que l'interaction interfaciale Dzyaloshinskii-Moriya (DMI) en raison de l'asymétrie d'inversion structurelle de FM sont considérés comme entraînant un mouvement DW chiral le long de la direction actuelle [9, 10]. Par conséquent, afin d'améliorer l'efficacité du CIDWM, il nécessite le HM avec un grand angle de spin Hall (θ _SH ) pour générer un couple plus important pour entraîner le mouvement DW. De nombreux efforts ont été consacrés pour obtenir un grand θ _SH des HM en faisant varier l'épaisseur de HM [11, 12], en décorant l'interface entre HM et FM [13, 14], en modifiant la cristallinité de HM [15], et même en impliquant de l'oxygène dans HM [16]. En outre, certains rapports atteignent également une grande efficacité θ _SH basé sur les structures HM/FM/HM, dans lesquelles deux couches HM ont le signe opposé de θ _SH [17,18,19]. Lorsqu'un courant traverse les deux couches HM, les courants de spin générés par deux types de couches HM fonctionneront de concert pour améliorer l'efficacité du SOT afin de diminuer la densité de courant pour commuter la magnétisation ou entraîner le mouvement DW. Pendant ce temps, la force DMI dans ce type de tricouches peut être différente de celle des bicouches, car il existe deux interactions interfaciales des deux côtés de la couche FM. Il a été constaté que la force DMI a une grande influence sur la vitesse DW lorsqu'un modèle de coordonnées collectives étendu a été proposé pour expliquer le comportement d'inclinaison DW [20]. De plus, l'inclinaison DW a également été signalée dans les micro-fils GaMnAs [20,21,22].

Dans nos travaux précédents, nous avons étudié l'effet de l'insertion d'une couche intermédiaire de C entre Co et Ta sur le champ d'anisotropie, le champ de commutation et les champs effectifs SOT dans les structures Pt/Co/Ta avec PMA [23]. La densité de courant de commutation d'aimantation obtenue est de l'ordre de 10 ⁶ A/cm ² dans les appareils Pt/Co/Ta et Pt/Co/C/Ta. Dans ce travail, nous étudions le mouvement DW induit par le courant et le comportement d'inclinaison dans ces deux échantillons et l'influence de l'insertion de C sur la force DMI et la vitesse DW dans des hippodromes Pt/Co/Ta de petite taille. Nous avons trouvé un petit changement de la constante d'échange DMI calculée (|D |), indiquant que la force du DMI provient principalement de la contribution de l'interface Pt/Co dans les stacks Pt/Co/Ta et Pt/Co/C/Ta. Dans le mouvement DW induit par le champ, la vitesse DW mesurée dans Pt/Co/C/Ta est plus petite que celle dans Pt/Co/Ta même sous un champ magnétique important, révélant que la barrière de potentiel de blocage a une grande influence sur le mouvement DW. En outre, dans le CIDWM, une vitesse DW plus grande est observée par rapport à celle du mouvement induit par le champ avec la même amplitude entre le champ effectif généré par le courant et le champ magnétique appliqué. Il révèle que le chauffage Joule généré par le courant affecte également le mouvement DW. Plus important encore, le phénomène d'inclinaison DW induit par le courant est observé dans les empilements Pt/Co/Ta et Pt/Co/C/Ta, ce qui peut être bien expliqué par le champ d'Oersted généré par le courant combiné au champ effectif de spin Hall.

Méthodes

Deux piles de films Ta(3)/Pt(5)/Co(0.6)/Ta(5) et Ta(3)/Pt(5)/Co(0.6)/C(2)/Ta(5) (épaisseur en nm) ont été déposés sur des substrats de verre corning à température ambiante par pulvérisation cathodique magnétron à courant continu avec une pression de base inférieure à 4,0 × 10 ⁻⁵ Pa. Le Ta inférieur de 3 nm est utilisé comme couche d'ensemencement, et la couche de Ta supérieure a un TaO_x d'environ 1,5 nm. couche de coiffage due à l'exposition à l'air [17, 24]. Ensuite, les piles de films ont été modelées en pistes de course de 8,5 μm et 3,0 μm de large pour Pt/Co/Ta et Pt/Co/C/Ta, respectivement, en utilisant des techniques de lithographie standard et de fraisage Ar-ion pour étudier le CIDWM. De plus, les barres Hall de 8,5 μm de large modelées selon les mêmes techniques ont été utilisées pour mesurer le champ hors plan (H _z résistance de Hall anormale )-dépendante (R _Salle ) à différents champs de polarisation dans le plan (H _x ) le long de la direction du courant pour atteindre le champ effectif de spin Hall (H _ELLE ) et estimer la force du DMI tel que rapporté par Pai et al. [25]. Dans leur rapport, le changement de R _Salle -H _z boucles à H _x peut être bien expliqué par un modèle chiral de Néel DW. Le quart de travail a été défini comme H _ELLE , qui peut être utilisé pour quantifier l'efficacité SOT χ ≡ H _ELLE /J (J est la densité de courant de charge). La méthode a été utilisée pour caractériser la force DMI et l'efficacité SOT dans ce travail. De plus, un microscope Kerr magnéto-optique avec effet Kerr polaire a été utilisé pour surveiller le mouvement DW sous le champ appliqué ou l'impulsion de courant à température ambiante.

Résultats et discussion

Sur la base du modèle chiral de Néel DW, nous avons d'abord étudié les boucles de Hall anormales sous le champ de polarisation dans le plan H _x pour obtenir la force DMI et l'efficacité SOT (voir le fichier supplémentaire 1). Le champ effectif DMI obtenu (H _DMI ) pour Pt/Co/Ta et Pt/Co/C/Ta est d'environ 1370 et 1055 Oe, respectivement. Le χ saturé (χ ^samedi ) correspondant à l'efficacité SOT la plus élevée est d'environ 10,0 et 8,3 Oe/(10 ⁶ A/cm ² ) pour Pt/Co/Ta et Pt/Co/C/Ta, respectivement. La diminution χ ^samedi pour Pt/Co/C/Ta peut être en ce qu'une certaine interdiffusion et réaction chimique de l'interface entre Co et C ainsi que l'interface entre C et Ta augmentent la probabilité de retournement de spin et réduisent l'injection effective de courant de spin à partir du Ta supérieur . De plus, la force de la constante d'échange DMI |D | peut également être calculé à partir du |H mesuré _DMI | en utilisant |D | = μ ₀ M _s ∆ |H _DMI | [26], où ∆ est la largeur DW et se rapporte à la constante de rigidité d'échange A et densité d'énergie PMA effective K _eff via ∆ = (A /K _eff ) ^1/2 . Utilisation de M _s (respectivement environ 1,213×10 ⁶ et 1,288×10 ⁶ A/m pour Pt/Co/Ta et Pt/Co/C/Ta) et K _eff (respectivement environ 4,1×10 ⁵ et 2,1×10 ⁵ J/m ³ pour Pt/Co/Ta et Pt/Co/C/Ta) comme indiqué dans le travail précédent et en supposant A ≈ 1. 5 × 10 ⁻¹¹ J/ m [27], on estime |D | = 1,01 ± 0,16 mJ/ m ² pour Pt/Co/Ta et |D | = 1.15 ± 0.14 mJ/ m ² pour Pt/Co/C/Ta. La différence de |D | valeur semble faible dans ces deux échantillons. Cela peut s'expliquer par le fait que la puissance totale du DMI résulte des deux contributions des interfaces inférieures Pt/Co et supérieures Co/Ta ou Co/C. Étant donné que les interfaces Pt/Co inférieures sont très similaires, elles contribuent également à |D |. Alors que pour la contribution de l'interface supérieure Co/Ta ou Co/C, Ma et al. [28] ont signalé que |D | induite par Ta est beaucoup plus faible que celle par Pt. Par conséquent, l'interface supérieure Co/Ta est faible pour la contribution du total |D |. Et la contribution de l'interface supérieure Co/C est également négligeable en raison du très faible couplage spin-orbite de C. Il est également noté que les interfaces inférieure Pt/Co et supérieure Co/Ta contribuent au DMI mais peuvent partiellement annuler l'un de l'autre [28], ce qui entraîne une légère diminution de |D | pour les échantillons Pt/Co/Ta par rapport aux échantillons Pt/Co/C/Ta. En conséquence, le |D similaire | pour les échantillons Pt/Co/Ta et Pt/Co/C/Ta révèle que la force du DMI provient principalement de la contribution de l'interface Pt/Co. De plus, pour ces deux échantillons, H _DMI /H _K (respectivement autour de 0,2 et 0,3 pour Pt/Co/Ta et Pt/Co/C/Ta) est inférieur à 2/π. Tandis que H _DMI n'est pas au-delà du seuil théorique requis pour stabiliser les Néel DWs [25, 26], le Néel DW chiral dans ces deux échantillons est démontré en observant le comportement CIDWM qui sera discuté ci-dessous. Pendant ce temps, le Hall anormal boucle sous le champ de polarisation dans le plan (H _y ) orthogonale à la direction du courant sont également étudiées. Même si un grand H _y est appliqué, le décalage de R _Salle -H _z loops est assez petit (voir le fichier supplémentaire 1). Cela pourrait être dû à ce H _y transforme progressivement les DW chiraux de type Néel en DW de type Bloch, et le champ effectif H _ELLE est proche de zéro pour un DW de type Bloch selon la formule [10, 29, 30] :

où, θ _ELLE , Mme , t _F , J _x , \( \widehat{m} \) et \( \widehat{j} \) représentent l'angle Hall de spin effectif, l'aimantation à saturation de la couche FM, l'épaisseur de la couche FM, la densité de courant le long de x direction, vecteur unitaire de l'aimantation et vecteur unitaire de la densité de courant, respectivement.

Ensuite, la vitesse DW (v ) sous le champ magnétique hors du plan et l'impulsion de courant dans le plan ont été mesurés à l'aide du microscope Kerr pour étudier le comportement du mouvement DW. Un DW pré-préparé a été formé en utilisant une impulsion de champ magnétique juste au-dessus du champ de nucléation après que l'hippodrome ait été saturé à un grand champ magnétique opposé. Vitesse sous H _z l'impulsion est montrée dans la Fig. 1a, b pour deux échantillons. Pour Pt/Co/C/Ta, v est encore plus petit que celui de l'échantillon Pt/Co/Ta même sous un champ magnétique d'entraînement important. Cela est peut-être dû à la formation beaucoup plus importante de défauts après la décoration C, ce qui augmente les champs d'épinglage [23]. On peut aussi voir que lgv est proportionnel à H _z ^-1/4 , indiquant un régime de fluage du mouvement DW selon la loi de fluage [31] :

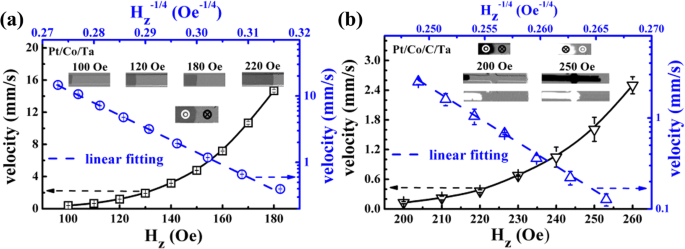
Vitesse DW en fonction du champ hors plan H _z pour Pt/Co/Ta (a ) et Pt/Co/C/Ta (b ). Les encarts dans a et b représenter les instantanés de domaines dans différents champs pour afficher la forme DW

où U _C est une énergie caractéristique liée au potentiel de blocage induit par le désordre, k _B est la constante de Boltzmann, T est la température, et H _dép. est le champ d'épinglage auquel l'énergie de Zeeman est égale à l'énergie d'épinglage DW. La pente d'ajustement donne une mesure de \( \frac{U_c}{k_BT}{H_{dep}}^{1/4}=s \), s est d'environ 37,4 et 76,5 Oe ^1/4 pour Pt/Co/Ta et Pt/Co/C/Ta, respectivement. Depuis le H _dép. pour Pt/Co/C/Ta est deux fois plus grande que celle pour Pt/Co/Ta [23], la différence de H _dép. ^1/4 entre eux est inférieur à 1,5. Cependant, la différence de s entre eux est supérieur à 2. Cela indique que l'échantillon Pt/Co/C/Ta a un potentiel de fixation plus important, ce qui est cohérent avec la discussion ci-dessus. De plus, les encarts de la figure 1a, b montrent également les instantanés d'images de domaine sous différents champs magnétiques. On peut voir que la forme DW montre une distribution plus grande pour Pt/Co/C/Ta que celle pour Pt/Co/Ta. Cela indique également que le potentiel d'épinglage n'est pas tout à fait homogène dans Pt/Co/C/Ta en raison de la décoration en C induisant des sites d'épinglage distribués de manière aléatoire. Considérant que, l'inclinaison DW régulière sous le champ magnétique n'est pas observée pour ces deux échantillons, ce qui est différent du modèle de coordonnées collectif théorique [20].

Par la suite, le comportement du CIDWM a également été étudié pour faire une comparaison avec le mouvement DW induit par le champ. Un domaine up-to-down (UD) ou down-to-up (DU) a d'abord été nucléé par un champ magnétique d'impulsion à partir d'un état saturé, puis un courant d'impulsion a été appliqué pour pousser le mouvement DW à l'aide d'un générateur d'impulsions avec largeur d'impulsion comprise entre 5 et 100 ns. La figure 2a, b montre la vitesse CIDWM sans aucun champ magnétique appliqué. La vitesse positive ou négative signifie le mouvement DW le long ou contre la direction actuelle. Cela implique la formation d'un Néel DW chiral avec l'existence de DMI dans ces deux échantillons [10, 30]. L'augmentation de la vitesse à la densité de courant plus élevée est due à l'augmentation de H _ELLE agissant sur la chirale Néel DW. Cependant, il faut une densité de courant deux fois plus grande pour atteindre la même vitesse DW dans les structures Pt/Co/C/Ta par rapport à celle dans les structures Pt/Co/Ta. Cela peut être attribué à la diminution de l'efficacité du SOT et à l'augmentation de la barrière potentielle d'épinglage par la décoration interfaciale en C. De plus, la vitesse DW par entraînement actuel est d'environ 10 ³ fois plus grand que celui provoqué par le champ magnétique, le champ effectif généré par le courant conservant la même valeur que le champ magnétique. Il révèle que d'autres mécanismes tels que le chauffage Joule et/ou le champ d'Oersted généré à partir du courant peuvent également jouer un rôle important dans le CIDWM. Il convient de noter, dans la Fig. 2b ainsi que dans la Fig. 3c, que les diminutions de la vitesse DW et de l'angle d'inclinaison DW sont observées dans l'échantillon Pt/Co/C/Ta lorsque la densité de courant est à ± 19,2 MA/cm ² . Pendant ce temps, on peut voir plus de zone de nucléation comme des points blancs ou noirs dans l'encart des figures. 2b et 3c à des densités de courant plus élevées. Cela pourrait être attribué au fait que le thermique active certains sites de nucléation aléatoires à de fortes densités de courant en raison du grand chauffage Joule existant et que le paysage de barrière de potentiel d'épinglage pourrait également être redistribué, ce qui peut exercer une influence sur la vitesse de mouvement et l'angle d'inclinaison.

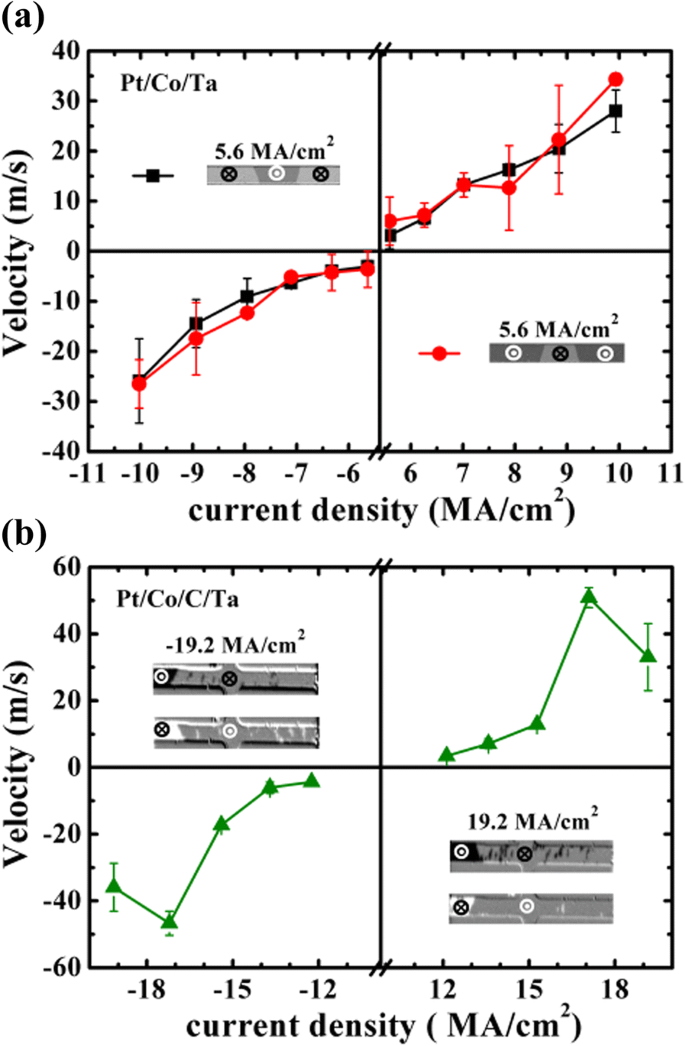
Vitesse DW contre densité de courant pour Pt/Co/Ta (a ) et Pt/Co/C/Ta (b ). Les encarts dans a et b représentent les instantanés de la forme du domaine à la densité de courant représentative

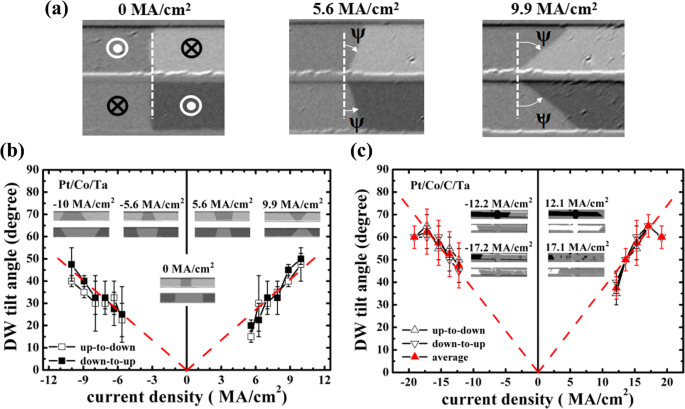
(un ) Les images Kerr donnent la définition de l'angle d'inclinaison DW (ψ ) et les modifications de ψ à différentes densités de courant de l'état "haut" à "bas" et "bas" à "haut", en prenant l'échantillon Pt/Co/Ta comme exemple. Angle d'inclinaison DW par rapport à la densité de courant pour Pt/Co/Ta (b ) et Pt/Co/C/Ta (c ). Les encarts dans b et c représentent les instantanés de la forme du domaine à différentes densités de courant

Pendant le mouvement DW induit par le courant, le phénomène d'inclinaison DW est clairement observé dans ces deux échantillons et l'inclinaison se forme progressivement dans une observation dépendante du temps avec une impulsion suffisamment courte comme force motrice. Afin d'avoir un aperçu de l'inclinaison DW induite par le courant, nous mesurons l'angle d'inclinaison DW (ψ ) qui est défini sur la Fig. 3a à différentes densités de courant. Il convient également de noter que l'angle d'inclinaison peut légèrement changer pendant le mouvement en raison de la large distribution de dépilage le long des pistes de course, ce qui entraînera une erreur de mesure importante à une densité de courant spécifique. À partir de la figure 3b, c, on peut voir une dépendance à peu près linéaire de l'angle d'inclinaison sur la densité de courant pour les deux échantillons. Il est en accord avec les travaux théoriques précédents [20], dans lesquels des dépendances approximativement linéaires de l'angle d'inclinaison et de la vitesse DW sur la densité de courant inférieure peuvent être observées. Cependant, un grand angle d'inclinaison DW se produit avec au moins un ordre de densité de courant plus élevée dans leur simulation. Ceci n'est pas cohérent avec notre observation et le comportement d'inclinaison n'est pas non plus observé pendant le mouvement DW induit par le champ dans notre expérience. Par conséquent, l'influence du DMI ou de la distribution graduée de la barrière de potentiel d'épinglage sur l'inclinaison DW induite par le courant peut être faible. En outre, l'effet Hall anormal peut également conduire à l'inclinaison du DW, mais la contribution devrait être faible dans une piste de course d'un nanomètre d'épaisseur [20]. Une explication possible est que le courant appliqué ne génère pas seulement un champ effectif de spin Hall H _ELLE , mais aussi le champ Oersted (H _Oersted ) qui peut également conduire à un mouvement DW. Les deux H _ELLE et H _Oersted pourrait avoir une influence sur l'inclinaison du DW. Sur la figure 4, nous traçons le schéma de ces champs effectifs pour clarifier le comportement d'inclinaison DW. L'arrangement du domaine est représenté par des croquis U-D-U-D, et la magnétisation dans le DW avec une chiralité gaucher est représentée par une fine flèche noire le long de l'orientation dans le plan. Dans une piste de course uniforme et mince, si l'épaisseur (t ) est bien inférieure à la largeur (w ), le H généré _Oersted est concentré sur les deux bords et sa composante moyenne sur l'épaisseur peut être calculée par H _Oersted = ±jt [3 + 2lnw /t ]/4π [22]. Le H obtenu _Oersted sont d'environ 19,6 et 37,4 Oe pour Pt/Co/Ta et Pt/Co/C/Ta en utilisant la densité de courant maximale de 10,0 et 19,2 MA/cm ² , respectivement, qui est comparable au champ effectif de spin Hall H _ELLE (environ 100,0 et 159,4 Oe pour Pt/Co/Ta et Pt/Co/C/Ta aux mêmes densités de courant). Depuis H _ELLE et H _Oersted ont la même direction aux positions marquées comme des étoiles vertes, un champ effectif plus grand agira sur le DW au niveau de la zone de l'étoile verte, ce qui se traduit par une vitesse beaucoup plus grande par rapport à celle de la zone opposée des étoiles vertes de la piste. Par conséquent, un DW inclinable avec une forme trapézoïdale spécifique peut être formé, illustré dans le panneau inférieur gauche de la figure 4. L'encart de la figure 3b pour Pt/Co/Ta montre également évidemment la forme similaire à certaines densités de courant représentatives. De plus, l'angle d'inclinaison accru à la densité de courant plus élevée peut s'expliquer par la grande différence de vitesse dans les deux bords de la piste en raison de l'augmentation de H _Oersted . Pendant ce temps, on peut constater que la forme du domaine subira une transformation une fois que les arrangements de domaine et/ou la polarité actuelle changeront selon l'analyse ci-dessus. Toute la forme du domaine esquissé à une impulsion de courant est cohérente avec les observations expérimentales. De plus, l'explication ci-dessus concernant l'inclinaison DW est également valable lorsqu'un H dans le plan _x ou H _y est appliqué. Lorsque H _x est appliqué, cela changera l'orientation de la magnétisation dans les DW. Par conséquent, le H _ELLE changera un signe pour le DW avec sa magnétisation horizontale d'origine opposée à H _x , ce qui agrandit ou rétrécit le domaine trapézoïdal (selon le signe de H _x ) comme indiqué dans le panneau central droit de la Fig. 4. Lorsque H _y est appliqué, un fort H _y changera un DW de type Néel en un Bloch. H _ELLE deviendra zéro selon l'équation. (1), et uniquement le champ Oersted généré actuellement H _Oersted entraîne le mouvement DW. Cela permettra au domaine de s'étendre sur un bord. On peut aussi voir que le changement de domaine au bord se fait comme H _y est d'environ − 1400 Oe, comme indiqué dans le panneau inférieur droit de la figure 4. Ceci est cohérent avec l'analyse selon laquelle H _Oersted car la seule force motrice est responsable du mouvement DW. Cependant, cela ne peut pas conduire à un comportement d'inclinaison DW régulier. Par conséquent, l'inclinaison DW induite par le courant pourrait être attribuée au champ d'Oersted induit par le courant combiné au champ effectif de spin Hall.

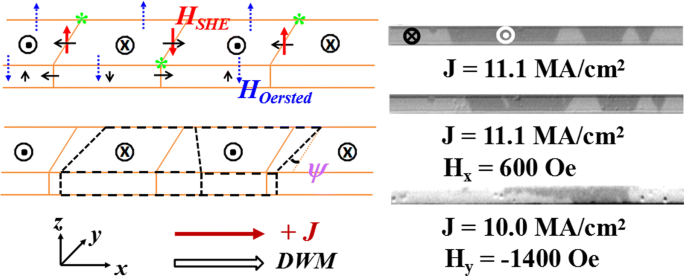
Mouvement DW schématique et formes de domaine à une densité de courant J . Le panneau supérieur gauche montre le domaine avec des croquis U-D-U-D et l'orientation de la magnétisation (fine flèche noire) dans le domaine et les DW. Une fois un courant appliqué, le H généré _ELLE agissant sur les DW sont représentés par des flèches rouges épaisses, tandis que les champs Oersted (H _Oersted ) des deux côtés de l'hippodrome sont représentés par des flèches bleues en tirets. Le panneau inférieur gauche montre le changement correspondant de la forme du domaine (indiqué par des blocs noirs épais en tirets) sous l'action de H _ELLE et H _Oersted . Le panneau de droite montre l'effet des champs magnétiques dans le plan sur la forme du domaine pour Pt/Co/Ta

Conclusions

En résumé, le mouvement et l'inclinaison de la paroi du domaine induits par le courant sont observés dans les structures Pt/Co/Ta et Pt/Co/C/Ta. La force DMI et l'efficacité SOT sont obtenues à l'aide d'une méthode de mesure de transport pouvant atteindre 1,01 ± 0,16 (1,15 ± 0,14) mJ/m ² et 10,0 (8,3) Oe/MA/cm ² pour les échantillons Pt/Co/Ta (Pt/Co/C/Ta), respectivement. La force DMI similaire pour les échantillons Pt/Co/Ta et Pt/Co/C/Ta révèle que la force DMI provient principalement de la contribution de l'interface Pt/Co. La vitesse DW réduite dans le mouvement DW induit par le champ pour Pt/Co/C/Ta indique que la vitesse DW est liée à la barrière de potentiel de blocage. De plus, le chauffage Joule généré par le courant et le champ d'Oersted jouent un rôle important dans le mouvement et l'inclinaison du DW. Pour l'application de mémoire de piste de course, le grand champ Oersted généré par le courant doit être pris en compte car il modifiera considérablement la forme des bits d'enregistrement et réduira même la zone des bits d'enregistrement. Cela peut ne pas être bénéfique pour l'application pratique. Nos découvertes pourraient fournir des perspectives de conception pour piloter le mouvement DW dans les mémoires de piste basées sur SOT.

Abréviations

CIDWM :

Mouvement de paroi de domaine induit par le courant

DMI :

Interaction Dzyaloshinskii-Moriya

D-U :

De bas en haut

DW :

Mur de domaine

FIDWM :

Mouvement de paroi de domaine induit par le champ

FM :

Ferromagnétiques

HM :

Métal lourd

PMA :

Anisotropie magnétique perpendiculaire

SOT :

Couple de rotation en orbite

STT :

Couple de transfert d'essorage

U-D :

De haut en bas