Conception d'un absorbeur térahertz ultra large bande accordable basé sur plusieurs couches de rubans de graphène

Contexte

Ces dernières années, la bande térahertz est devenue l'une des plateformes les plus intéressantes en raison de l'énorme application en spectroscopie, imagerie médicale, modulateurs, sécurité et communication [1,2,3]. L'absorbeur térahertz est une branche importante, qui peut trouver des applications pratiques dans les domaines ci-dessus [4,5,6]. Cependant, la bande passante étroite, la faible efficacité d'absorption et les performances d'absorption non réglables des absorbeurs limitent considérablement leurs applications dans la pratique. Afin de mieux étendre l'application de l'absorbeur térahertz, davantage de nouveaux dispositifs et matériaux sont nécessaires de toute urgence. Le graphène, en tant que matériau bidimensionnel avec la structure en treillis en nid d'abeille, est devenu l'un des matériaux les plus prometteurs en raison de sa capacité d'accord de conductivité contrôlée par le champ électrique, le champ magnétique, la tension de grille et le dopage chimique [7,8,9,10 ,11,12,13,14]. En particulier, le graphène peut supporter des plasmons de surface dans les gammes térahertz. Par rapport au matériau plasmon de surface traditionnel, les plasmons de surface au graphène présentent l'avantage de faibles pertes, d'une accordabilité flexible, etc. [15,16,17,18,19].

En raison de la supériorité des matériaux de graphène dans les absorbeurs térahertz, certains absorbeurs de graphène ont été proposés et démontrés [20,21,22,23,24,25,26,27,28,29,30,31,32,33 ,34]. L'analyse théorique confirme qu'une seule couche de graphène est optiquement transparente et qu'elle a une absorption de 2,3% [35,36,37]. Pour améliorer le confinement de l'énergie électromagnétique, des structures de graphène à motifs périodiques ont été conçues, telles qu'en forme de filet [20,21,22], d'anti-points [23] et en forme de croix [32]. Cependant, ces absorbeurs dépendent profondément du graphène structuré complexe qui entraîne des difficultés de fabrication. De plus, la bande disponible pour l'exploitation est très étroite, et la plupart des œuvres rapportées n'ont pas une bande passante supérieure à 1,5 Thz [20,21,22,23,24,25,26,27,28]. Afin d'élargir la bande passante, plusieurs structures de graphène multicouches ont été proposées. Cependant, les structures multicouches rapportées dépendent également de la structure très complexe du graphène, et les bandes passantes de fonctionnement ne sont pas assez longues [32,33,34]. De plus, Zhao et al. conçu un absorbeur térahertz commutable pour l'application d'un modulateur d'amplitude [25]. En contrôlant le potentiel chimique du graphène de 0 à 0,3 eV, l'état de la structure conçue peut passer de l'absorption (> 90 %) à la réflexion (> 82 %) dans la gamme de fréquences de 0,53 à 1,05 Thz. Mais l'intensité de commutation n'est pas assez élevée et la bande passante de modulation est très étroite, ce qui limite son application ultérieure dans la pratique.

Dans cet article, nous présentons un absorbeur térahertz accordable à base de graphène composé de graphène multicouche qui peut atteindre une absorption ultra large bande de plus de 90 % dans la gamme de fréquences de 3 à 7,8 Thz. La capacité d'absorption moyenne de l'absorbeur est supérieure à 96,7 %. En outre, l'absorbeur proposé a une intensité de commutation plus élevée, l'amplitude d'absorption peut être réglée d'une absorption presque parfaite (> 90 %) à une réflexion élevée (> 90 %) en modifiant l'énergie de Fermi de la couche de graphène dans toute la bande passante de 4,8 Thz. Lorsque l'énergie de Fermi du graphène est de 0 eV, la structure proposée sera un réflecteur presque parfait avec une réflexion de plus de 97% dans la bande des hautes fréquences (environ 5,5 Thz plus tard). De plus, l'absorbeur est indépendant des angles d'incidence avec une absorption supérieure à 90 % jusqu'à 50°. À notre connaissance, nous proposons d'abord la structure bidimensionnelle multicouche graphène/diélectrique pour réaliser une absorption ultra-large bande. L'absorbeur proposé est simple et ne dépend pas du graphène à motifs complexes, et la conception offre une grande commodité pour la fabrication de structures de graphène multicouches [38, 39]. Il est important de noter que la conception est évolutive pour développer des absorbeurs térahertz accordables plus larges en ajoutant plus de couches de graphène, ce qui peut avoir une large application dans les dispositifs optoélectroniques térahertz.

Méthodes

Le schéma de la structure proposée est illustré à la Fig. 1, qui se compose de graphène multicouche intégré dans le diélectrique sur le SiO₂ couche et une épaisse plaque réfléchissante métallique sur le fond. Comme le montre la figure 1, en haut, du graphène de largeur différente (W ) est noyé dans le diélectrique à un certain écart t ₂ (t ₂ = 2 µm). La largeur W de chaque graphène est de 5, 5, 27, 4, 4, 2, 21, 21 et 26 um, respectivement (de haut en bas). Chaque couche est symétrique par rapport au z -axe. La distance t ₁ entre le bas de la couche de graphène et le SiO₂ couche est de 2 um. L'épaisseur du diélectrique est H ₁ . La couche intermédiaire est SiO₂ avec une épaisseur de H ₂ . Le fond est un film métallique d'une épaisseur de D . La période de l'unité est P. Ces valeurs initiales des paramètres de structure sont définies sur H ₁ = 21 m, H ₂ = 7 m, D = 0,5 m, P = 32 µm. Le matériau métallique inférieur est de l'or, et sa permittivité peut être correctement représentée par le modèle Drude dans la gamme térahertz comme suit :

où la valeur de permittivité constante ε _∞ , fréquence plasma ω _p , et fréquence de collision γ sont réglés sur 1, 1,38 × 10 ¹⁶ rad/s, et 1,23 × 10 ¹³ s ^− 1 , respectivement. La permittivité du matériau diélectrique et SiO₂ matériel sont définis sur 3 et 4, respectivement.

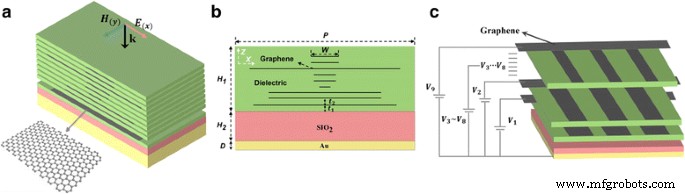
un Schéma de principe de l'absorbeur large bande à base de graphène. b Coupe transversale de l'absorbeur avec les paramètres utilisés pour le calcul. c Le schéma du circuit de polarisation externe. Les branches de la tension (V ₁ ~V ₉ ) sont respectivement connectés à différentes couches de graphène

Dans la simulation, le graphène est traité comme un film ultra-mince noyé dans le diélectrique. La conductivité de surface complexe du graphène dominée par les contributions interbandes et intrabandes peut être calculée en utilisant la formule de Kubo [40] :

où \( {f}_d\left(\varepsilon \right)={\left({e}^{\left(\varepsilon -{E}_f\right)/{k}_BT}+1\right)} ^{-1} \) est la distribution de Fermi-Dirac, w est la fréquence radian, ε est l'énergie, k _B est la constante de Boltzmann, τ est le temps de relaxation du porteur, T est la température (T = 300 K dans notre article), ℏ est la constante de Plank réduite, et E _f est l'énergie de Fermi. La formule de Kubo (2) indique que la conductivité de surface du graphène complexe peut être ajustée par l'énergie de Fermi E _f . L'énergie du graphène Fermi de chaque couche peut être contrôlée individuellement par la tension polarisée, la relation entre E _f et la tension polarisée peut être écrite comme [41, 42] :

où v _F = 0.9 × 10 ⁶ m/s est la vitesse Femi, V ₀ est le décalage de tension [41], \( {a}_0=\frac{\varepsilon_0{\varepsilon}_d}{ed} \), a ₀ est le modèle capacitif de la structure, où ε ₀ est la permittivité dans le vide. ε _d est la permittivité du diélectrique, d est la hauteur du diélectrique, et e est la charge d'un électron. V _n (V ₁ ~V ₉ ), c'est-à-dire que la tension appliquée au graphène peut être obtenue à partir du circuit supplémentaire de la figure 1c. Selon les formules (2) et (3), la conductivité de surface du graphène peut être contrôlée par la tension appliquée. Ensuite, en se basant sur la loi d'Ampère en régime stationnaire et la loi d'Ohm, la permittivité du graphène peut être obtenue comme [43] :

Dans lequel t _g est l'épaisseur du graphène, ε ₀ est la permittivité du vide, et σ _g est la conductivité de surface du graphène. Selon la formule (4), la permittivité du graphène peut être obtenue par la conductivité de surface, qui peut également être obtenue par la tension appliquée. Par conséquent, la formule (2-4) indique que les propriétés électromagnétiques du graphène peuvent être contrôlées dynamiquement par la tension appliquée, ce qui permet également de contrôler dynamiquement les caractéristiques d'absorption de la structure.

Pour étudier les performances d'absorption de la structure conçue, nous mettons en œuvre les simulations numériques à l'aide d'un FDTD bidimensionnel. Dans notre simulation, nous définissons la structure sur une condition aux limites périodique dans la direction x. Un faisceau d'onde plane térahertz est incident sur le modèle normalement le long du z direction avec son champ électrique E le long de x direction. La condition aux limites de Bloch est appliquée à l'incidence oblique dans la structure périodique. Nous utilisons 1-R-T pour calculer l'absorption du modèle, où R et T représentent respectivement la réflectivité et la transmissivité. Etant donné que l'épaisseur du métal est bien supérieure à la profondeur de peau de la lumière incidente dans le métal, la transmissivité T est nulle. Ainsi, nous simplifions la formule de calcul pour 1-R.

Résultats et discussion

Tout d'abord, nous ajustons la tension de chaque couche de graphène pour obtenir une absorption parfaite (de haut en bas, nous ajustons finement l'énergie de Fermi E _f de chaque couche de graphène à 0,9, 0,9, 1,1, 0,8, 0,8, 1,1, 1,1, 0,9 et 0,8 eV). Comme le montre la figure 2, de 3 à 7,8 Thz, la structure proposée a une absorption à large bande supérieure à 90 % dans une bande passante de 4,8 Thz. La FWHM de l'absorbeur est de 5,4 Thz. La bande passante est d'environ \( \frac{BW}{f_0}\times 100\% \) = 88,8% de la fréquence centrale (ici, BW est la bande passante et f ₀ est la fréquence centrale). Nous calculons également la capacité d'absorption moyenne de l'absorbeur, qui atteint 96,7 %. En revanche, avec le E _f = 0 eV, la structure proposée sera un réflecteur quasi idéal avec une réflexion de plus de 90 % sur toute la bande passante de fonctionnement, et dans la bande haute fréquence (environ 5,5 Thz plus tard), la réflexion même supérieure à 97 %. Bien sûr, nous pouvons également régler la tension de chaque couche de graphène pour obtenir l'amplitude souhaitée, ce qui peut avoir des applications potentielles dans certains domaines.

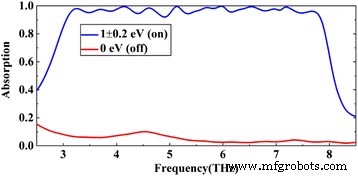
Les spectres d'absorption calculés de l'absorbeur proposé, où la ligne bleue représente l'absorption à haute tension et la ligne rouge indique l'absorption sans tension appliquée

Afin d'expliquer l'absorption quasi parfaite dans une bande passante ultra-large, nous discutons tout d'abord de la situation d'une seule couche de graphène. Comme le montre la figure 3a, nous concevons la structure avec une seule couche de graphène intégrée dans le diélectrique. Sur la base des plasmons de surface du graphène, nous étudions l'effet des paramètres liés au graphène sur les performances d'absorption de l'absorbeur, y compris l'énergie de Fermi E _f , la largeur W , et la position t de graphène.

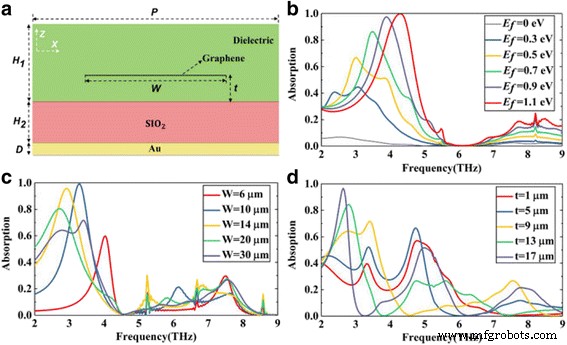
un Diagramme schématique d'une structure de graphène monocouche. b –d L'absorption de la largeur de la structure différente Fermi énergie E _f , largeur W , et positionnez t de la feuille de graphène, respectivement

La figure 3b montre l'influence de l'énergie du graphène Fermi E _f sur le spectre d'absorption avec W fixe et t . Comme l'augmentation de E _f , la résonance plasmonique de surface du graphène devient plus forte, l'absorption de la structure est plus élevée en conséquence. Le pic d'absorption encore plus de 99% à 4,3 Thz avec le E _f = 1,1 eV. Et le pic d'absorption de résonance se déplace vers une fréquence plus élevée, le décalage vers le bleu. De même, la figure 3c, d montre le spectre d'absorption de la structure avec différents W ou t avec E inchangé _f . En faisant varier le W ou t de la couche de graphène, l'amplitude et la fréquence du pic de résonance sont modifiées respectivement. Ce phénomène peut être expliqué par la théorie des circuits [28]. Dans cette théorie, le graphène est décrit comme une admittance de dérivation, puis le circuit équivalent de la structure peut être modélisé avec des lignes de transmission et une admittance de graphène. Selon des travaux antérieurs [28], l'admittance du graphène peut être modifiée par la largeur W et l'énergie Fermi E _f du graphène. De plus, l'admittance des lignes de transmission correspondant au diélectrique est liée à l'épaisseur du diélectrique. Dans notre structure, le diélectrique est séparé par une couche de graphène. Ainsi, la position t de la couche de graphène affecte également l'admittance d'entrée de la structure.

Comme nous l'avons vu ci-dessus, en raison de l'influence des paramètres liés au graphène sur l'admittance d'entrée de la structure, les pics d'absorption de résonance du modèle sont également influencés. Si l'admittance d'entrée de la structure correspond à l'admittance en espace libre, l'absorption presque parfaite à une certaine fréquence est obtenue.

Ensuite, afin d'obtenir une absorption à large bande, nous devons autoriser les pics d'absorption de résonance qui atteignent l'admittance correspondant à proximité les uns des autres. Comme les pics d'absorption sont suffisamment proches pour fusionner, une absorption à large bande est obtenue. Par conséquent, nous ajoutons des couches de graphène pour obtenir plus de pics d'absorption de résonance. Et en même temps, nous ajustons les paramètres qui affectent le pic de résonance, y compris E _f , W , et t pour mettre en œuvre l'appariement d'admission. Nous ajoutons d'abord deux couches de graphène. Comme le montre la figure 4a, trois couches de graphène avec une largeur différente W sont noyés dans le diélectrique. Il y a un certain intervalle t entre différentes couches de graphène ou le graphène inférieur du diélectrique. Nous ajustons les paramètres liés au graphène aux valeurs appropriées, où nous définissons t = 2 m, E _f = 0.9 eV, et W = 26, 21 et 20 m, respectivement (de bas en haut).

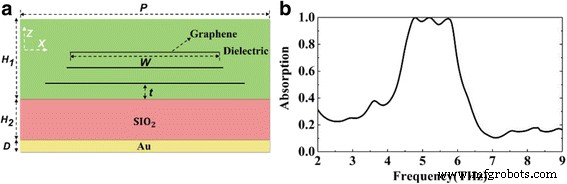
un Diagramme schématique d'une structure de graphène à trois couches. b Les spectres d'absorption calculés de la structure du graphène à trois couches

Comme le montre la figure 4b, la structure a une bande passante d'absorption presque parfaite de 1,3 Thz avec une fréquence centrale de 5,25 Thz. Trois pics de résonance à 4,7, 5,2 et 5,7 Thz sont obtenus correspondant à l'amplitude d'absorption de 99,9, 99,9 et 99,1 %, respectivement. Afin d'obtenir une absorption ultra-large bande, similaire à la structure de graphène à trois couches, nous ajoutons plus de couches de graphène et ajustons les paramètres de graphène de chaque couche de graphène aux valeurs appropriées. Nous supposons que les paramètres structurels sont fixés et que la production est terminée ; nous pouvons ajuster dynamiquement l'énergie de Fermi du graphène pour obtenir une absorption à large bande. Sur la base du principe de l'adaptation d'impédance et de l'expérience de recherche sur la structure de graphène à trois couches, nous supposons d'abord que le niveau de Fermi de chaque couche de graphène est de 1 eV. Comme le montre la figure 5 (a), l'absorption de la plupart des bandes est supérieure à 90 %, à l'exception des bandes « 1 » et « 2 ». La figure 5 (a–e) montre le processus d'ajustement progressif pour une parfaite absorption des bandes « 1 » et « 2 ». Selon la figure 6e, f, l'absorption de la dernière bande « 1 » est dominée par la quatrième couche (de bas en haut), nous ajustons donc l'énergie de Fermi de cette couche individuellement. Comme le montre la figure 7, lorsque l'énergie de Fermi est de 0,8 eV, les performances d'absorption sont les meilleures. En effet, l'énergie de Fermi affecte l'impédance du graphène, puis affecte l'impédance d'entrée de l'ensemble de la structure. L'énergie de Fermi plus grande ou plus petite du graphène entraînera une désadaptation d'impédance. De a à b, nous avons amélioré les performances d'absorption de la bande « 1 » (dans la bande avant « 1 », les courbes a et b se chevauchent approximativement). De même, nous constatons que la distribution d'énergie dans la bande « 2 » est principalement concentrée sur les 5e, 8e et 9e couches. Nous avons d'abord défini l'énergie de Fermi des 8e et 9e couches de graphène à 0,9 et 0,8 eV, respectivement. Comme le montre la figure 5, de b à c, en plus des creux "3" et "4", l'absorption de la bande restante dans "2" est supérieure à 90 %. Ensuite, selon la figure 6c, le pendage « 3 » est principalement influencé par la 5ème couche de graphène, nous avons réglé l'énergie de Fermi à 0,8 eV. De c à d, les performances d'absorption au creux « 3 » ont également été améliorées. Cependant, selon la figure 6d, le pendage « 4 » est affecté par toutes les couches de graphène. Par conséquent, nous ajustons l'énergie de Fermi de la couche de graphène restante à la valeur appropriée. De d à e, l'absorption à large bande presque parfaite est obtenue. Par rapport à la structure de graphène à trois couches illustrée à la figure 4, davantage de pics d'absorption de résonance sont obtenus, les pics d'absorption de différentes fréquences sont proches les uns des autres et superposés pour former une absorption ultra-large bande supérieure à 90 % avec une bande passante de 4,8 Thz.

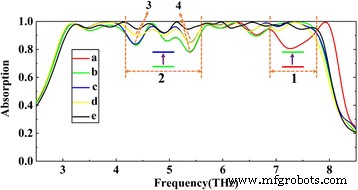
(a)–(e) montrent le processus d'ajustement progressif pour une absorption parfaite. L'énergie de Fermi de chaque couche de graphène (de bas en haut) est définie comme (a) [1] eV, (b) [1, 1, 1, 0,8, 1, 1, 1, 1, 1] eV, (c ) [1, 1, 1, 0,8, 1, 1, 1, 0,9, 0,8] eV, (d) [1, 1, 1, 0,8, 0,8, 1, 1, 0,9, 0,8] eV et (e) [0.9, 0.9, 1.1, 0.8, 0.8, 1.1, 1.1, 0.9, 0.8] eV

un –f Les distributions de l'amplitude du champ électrique (|E |) de l'absorbeur proposé à différentes fréquences

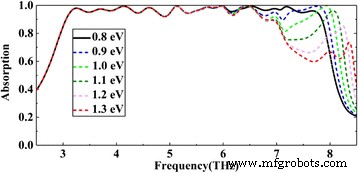
Spectres d'absorption avec différents E _f de la quatrième couche de graphène et avec E inchangé _f d'autres couches de graphène

Pour comprendre le mécanisme physique derrière l'absorption quasi-parfaite ultra-large bande, nous donnons également un calcul et une analyse détaillés des distributions d'amplitude de champ électrique (|E|) de la structure proposée à différentes fréquences de fonctionnement. Comme le montre la figure 6, l'énergie du champ lumineux est confinée entre les différentes couches de graphène et de diélectrique, conduisant à une forte absorption. Les caractéristiques des distributions de champ électrique sont cohérentes avec le spectre d'absorption montré sur la figure 2. À une certaine fréquence, par exemple, la figure 6b montre que le confinement du champ électrique est principalement dû au fort couplage du graphène et du diélectrique en raison de l'excitation. du plasmon de surface localisé (LSP), la figure 6d montre que les plasmas de surface de graphène jouent un rôle majeur dans le confinement du champ électrique. L'excitation du plasmon de surface localisé (LSP) et des plasmas de surface de graphène contribuent à la forte absorption ensemble. Les figures 6a, b, d et 6c, e, f montrent que le couplage fort entre le graphène et le diélectrique à une certaine fréquence peut être provoqué par le graphène multicouche ou le graphène monocouche, respectivement. L'empilement d'absorptions élevées à différentes fréquences crée une absorption à large bande sous l'action de toutes les couches de graphène.

Afin de mieux illustrer l'effet d'empilement, par exemple, selon la Fig. 6e, f, l'absorption de la dernière bande (environ 6,5 Thz plus tard) est principalement dominée par la quatrième couche de graphène (de bas en haut). Donc, nous ajustons la tension de cette couche de graphène. Comme le montre la figure 7, avec l'augmentation de l'énergie de Fermi de la quatrième couche de graphène, l'amplitude d'absorption de la bande après environ 6,5 Thz augmente progressivement, mais il n'y a presque aucun changement dans la bande avant 6,5 Thz. De même, nous pouvons également ajuster indépendamment une certaine bande principalement affectée par d'autres couches de graphène. Toutes les bandes qui peuvent être ajustées indépendamment pour une absorption élevée sont superposées pour former éventuellement une absorption à large bande. Comme pour l'analyse de la figure 7, le phénomène d'ajustement indépendant illustre en outre que l'effet d'empilement de toutes les couches de graphène permet d'obtenir une absorption à large bande presque parfaite.

Comme discuté ci-dessus, le couplage fort entre le graphène et le diélectrique joue un rôle majeur dans l'absorption à large bande. Dans les applications pratiques, nous espérons que l'absorption large bande est insensible aux angles d'incidence. Comme le montre la figure 8, nous étudions l'effet des angles d'incidence sur l'absorbeur. À partir de la figure 8, nous pouvons constater que l'absorbeur proposé est insensible aux angles d'incidence. Bien que l'angle d'incidence soit passé à 30°, les performances d'absorption de la structure ne sont pratiquement pas affectées. Lorsque l'angle incident augmente jusqu'à 50°, bien que l'efficacité d'absorption soit réduite, l'absorbeur maintient toujours une absorption élevée supérieure à 90 % dans toute la bande passante de fonctionnement. Par conséquent, l'absorbeur peut bien fonctionner avec une efficacité d'absorption élevée sur une large plage d'angles d'incidence.

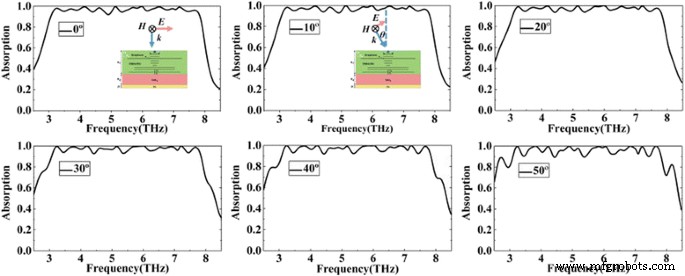
Les spectres d'absorption calculés de l'absorbeur avec différents angles d'incidence

Enfin, compte tenu des difficultés de fabrication de la structure multicouche, nous discutons de l'effet des paramètres de structure pertinents sur les performances de l'absorbeur. Les figures 9a, b montrent les spectres d'absorption de l'absorbeur proposé avec différentes épaisseurs de la couche diélectrique H ₁ et avec différentes épaisseurs de SiO₂ couche H ₂ , respectivement. Comme le montre la figure 9a, la hauteur la plus appropriée du diélectrique H ₁ est de 21 µm. Sur cette base, H ₁ augmenter ou diminuer de 0,5 µm, les performances de l'absorbeur ne changent pratiquement pas. Même si H ₁ change de 1 m, l'absorbeur maintient toujours une absorption supérieure à 90 % dans la plupart des bandes, à l'exception de la bande autour de 7 Thz. Comme le montre la figure 9b, par rapport à H ₁ , l'absorbeur est plus sensible à la hauteur du SiO₂ H ₂ . Même dans ce cas, en plus de la bande autour de 6 et 7,1 Thz, l'absorbeur conserve également de bonnes performances dans la plupart des bandes. Comme discuté ci-dessus, nous pouvons constater que bien que l'épaisseur de la couche diélectrique et le SiO₂ couche sont modifiées même à l'échelle du micron, l'absorbeur conserve toujours une bonne performance d'absorption dans la plupart des longueurs d'onde, ce qui améliorera considérablement la robustesse de l'absorbeur dans la fabrication.

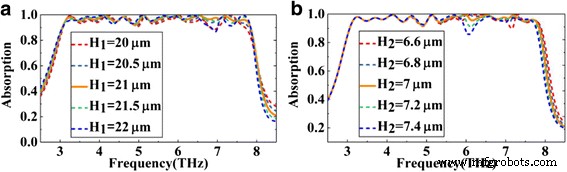
Les spectres d'absorption simulés de l'absorbeur proposé avec différentes épaisseurs de la couche diélectrique et avec différentes épaisseurs de SiO₂ couche correspondant à a et b

Conclusions

Dans cet article, nous proposons un absorbeur térahertz ultra large bande et accordable à base de graphène, constitué de multicouches de graphène/diélectrique. L'absorbeur proposé peut atteindre une absorption à large bande de plus de 90 % avec une bande passante de 4,8 Thz en modifiant l'énergie de Fermi E _f de différentes couches de graphène. Avec le E _f =0 eV, la conception proposée sera un réflecteur presque idéal avec une réflexion de plus de 90 % dans toute la bande passante de fonctionnement de 3 à 7,8 Thz. L'absorption ultra-large bande est attribuée à l'effet d'empilement d'une forte absorption de résonance à différentes fréquences excitées par des plasmons de surface localisés (LSP) et des plasmons de surface de graphène. De plus, l'absorbeur proposé est insensible aux angles d'incidence, et on constate également que l'épaisseur de la couche diélectrique et le SiO₂ couche a peu d'effet sur les performances d'absorption, ce qui est plus bénéfique pour les applications pratiques. De plus, l'absorbeur proposé est simple et ne dépend pas d'un graphène structuré complexe et la bande passante peut être élargie en ajoutant plus de couches de graphène. Cet absorbeur large bande accordable peut avoir de grandes applications potentielles dans les photodétecteurs, l'imagerie et les modulateurs.

Abréviations

FDTD :

Domaine temporel aux différences finies

LSP :

Plasmon de surface localisé