Transparence induite par plasmon accordable dynamiquement dans un système de guide d'ondes asymétrique couplé à la nanocavité à base de graphène

Contexte

La transparence induite par le plasmon (PIT), qui est un nouveau phénomène analogue à l'effet de transparence induite électromagnétiquement (EIT) générant une fenêtre de transparence nette dans un large spectre d'absorption [1], a attiré une grande attention en raison de ses applications potentielles dans un large éventail de tels que la lumière lente [2, 3], la commutation optique [4], le stockage de la lumière [5] et la détection à haute sensibilité [6, 7]. Les dispositifs basés sur PIT peuvent être réalisés avec une empreinte ultra-compacte en raison de la grande capacité d'amélioration du champ local et du dépassement de la limite de diffraction classique de la lumière fournie par les polaritons de plasmon de surface (SPP) [8, 9]. Une variété de conceptions ont été proposées pour obtenir l'effet PIT dans les nanostructures plasmoniques, y compris les systèmes de résonateurs couplés [10,11,12,13], les structures cristallines photoniques [14, 15] et les structures de métamatériaux [16, 17]. Cependant, la plupart de ces structures affichant un effet PIT sont à peine accordables à moins de modifier les paramètres géométriques des structures, ce qui limite dans une large mesure le contrôle actif des fenêtres PIT et dégrade la qualité.

Le graphène, une monocouche d'atomes de carbone disposés dans un réseau en nid d'abeilles bidimensionnel (2D) [18], présente un grand potentiel pour le développement de dispositifs optoélectroniques hautement efficaces en raison de ses propriétés électriques et optiques exceptionnelles, notamment sa capacité de confinement extrême [19,20, 21], une accordabilité dynamique et des pertes d'amortissement relativement faibles [22, 23]. En particulier, la conductivité de surface du graphène peut être réglée dynamiquement par le potentiel chimique via une tension de grille externe ou un dopage chimique [24, 25], ce qui fait du graphène un candidat prometteur pour la conception d'un PIT accordable alors que les paramètres géométriques sont fixes. En raison de ces caractéristiques extraordinaires par rapport à celles des métaux nobles conventionnels, un large éventail de recherches a été effectué pour réaliser le PIT à base de graphène, tels que les phénomènes PIT dans le guide d'ondes en graphène couplé à un résonateur en anneau de graphène [26, 27] et les effets PIT dans un guide d'ondes nanoruban à base de graphène couplé à une structure de résonateur rectangulaire en graphène [28, 29]. Sun et al. ont étudié la structure à double couche de graphène à motifs périodiques séparés par une couche diélectrique dans la gamme de fréquences térahertz, où les réponses PIT multispectrales ont été obtenues [30]. De plus, des effets PIT accordables sont réalisés dans les nanobandes de graphène périodiquement combinées et décrits analytiquement avec le modèle d'oscillateur de Lorentz couplé [31, 32]. Cependant, la plupart des travaux précédents portaient sur les résonateurs en graphène, couplés à un graphène monocouche ou à un système de guide d'ondes à nanoruban de graphène, et à des systèmes de nanobandes de graphène avec une lumière incidente normale. Il y avait très peu ou même pas d'études sur le phénomène de transparence induit plasmoniquement dans une feuille de graphène avec des potentiels chimiques localement variants. De plus, par rapport à la lumière incidente normale, la propagation dans le plan présente des avantages considérables pour l'intégration sur puce.

Motivés par les études fondamentales ci-dessus, dans cet article, nous proposons une nanostructure plasmonique à base de graphène composée d'un guide d'ondes de bus plasmonique couplé latéralement à une nanocavité en forme de U et une nanocavité rectangulaire sur la même monocouche de graphène. Le logiciel commercial COMSOL Multiphysics basé sur la méthode des éléments finis (FEM) est utilisé pour explorer la transmission et les réponses électromagnétiques de nos conceptions. Les résultats de simulation révèlent que le phénomène PIT est observé dans notre nanostructure plasmonique proposée. En outre, la fenêtre PIT peut être réglée efficacement en faisant varier les potentiels chimiques des nanocavités et du guide d'ondes du bus plasmonique. En outre, une théorie des modes couplés (CMT) est introduite pour expliquer les caractéristiques de transmission du phénomène PIT. Enfin, un capteur d'indice de réfraction plasmonique basé sur la nanostructure plasmonique proposée est étudié. La sensibilité de détection de 333,3 nm/unité d'indice de réfraction (RIU) est atteinte au pic de transmission PIT. De plus, l'effet de lumière lente avec un retard de groupe supérieur à 1 ps est réalisé. Cette nouvelle nanostructure plasmonique proposée peut offrir une nouvelle façon de réaliser l'intégration de dispositifs plasmoniques sur puce à haute densité à base de graphène sur une monocouche de graphène.

Méthodes

Par souci de simplicité, la structure proposée est modélisée par une monocouche de graphène suspendue avec une variation locale du potentiel chimique pour former le guide d'onde de bus correspondant et les nanorésonateurs. La figure 1a montre la configuration schématique et les paramètres géométriques d'une nanocavité en forme de U directement couplée à un guide d'onde de bus plasmonique. Le guide d'ondes couplé à une nanocavité en forme de U avec un potentiel chimique de μ _c2 est entouré par la même feuille de graphène avec un potentiel chimique de μ _c1 . La largeur du guide d'onde du bus plasmonique d est de 20 nm. La largeur et la hauteur de la nanocavité en forme de U sont W _U = 150 nm et L _U = 120 nm respectivement. La modélisation théorique exacte d'une telle structure nécessite un calcul en trois dimensions (3D), ce qui est extrêmement consommateur de temps et de mémoire. Pour résoudre ce problème, la méthode de l'indice effectif a été utilisée par de nombreuses publications [33,34,35], et l'indice de réfraction de la structure est remplacé par l'indice effectif des modes guidés, qui est défini par le rapport entre la constante de propagation et le nombre d'onde dans l'espace libre. Dans notre structure, la feuille de graphène est traitée comme un film ultrafin qui se caractérise par un indice effectif défini comme n _eff = β /k ₀ , où k ₀ = 2π /λ est le nombre d'onde dans l'espace libre. La constante de propagation β du mode SPP guidé pris en charge par le graphène monocouche s'écrit [36, 37]

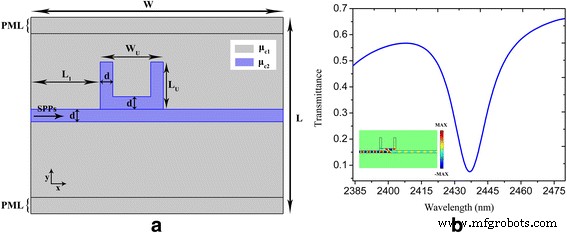
a, b La configuration schématique et les paramètres géométriques d'un système de guide d'ondes couplé à une nanocavité en forme de U et la transmittance spectrale correspondante respectivement. L'encart en b montre le champ électrique (E _y ) distribution à une longueur d'onde de 2437 nm. Les paramètres sont définis comme W = 800 nm, L = 620 nm, d = 20 nm, W _U = 150 nm, L _U = 120 nm, L ₁ = 220 nm, τ = 1 ps, μ _c1 = 0.3 eV, et μ _c2 =0,9 eV. Les couches parfaitement assorties (PML ) d'une largeur de 50 nm sont implémentés sur le top et en bas du domaine de calcul pour éliminer les réflexions indésirables de la limite du domaine

où μ ₀ et ε ₀ représentent la perméabilité et la permittivité du vide, respectivement, et μ _r et ε _r représentent respectivement la perméabilité relative et la permittivité relative. La conductivité de surface du graphène σ _g composé des transitions électroniques interbandes σ _inter et la diffusion intrabande électron-photon σ _intra est donnée par la formule de Kubo [38, 39]

Avec

où μ _c est le potentiel chimique du graphène, ω est la fréquence angulaire du plasmon, ћ est la constante de Planck réduite, e est la charge électronique, k _B est la constante de Boltzmann, T est la température, ℏ = h/2π est la constante de Planck réduite, et τ est le temps de relaxation du moment de l'électron. Plus précisément, le potentiel chimique du graphène peut être réglé via un dopage chimique ou une synchronisation électrique [25, 26]. Mikhaïlov et al. ont montré expérimentalement que la densité de porteurs dans une feuille de graphène aussi élevée que 10 ¹⁴ cm ⁻² avait été atteint, ce qui a conduit à un potentiel chimique de 1 à 2 eV à une température inférieure à 250 K [40]. De plus, il a été démontré que le graphène en suspension de haute qualité avec une mobilité en courant continu aussi élevée que 10 ⁵ cm ² V ⁻¹ s ⁻¹ peut être obtenu, ce qui correspond à τ> 1,5 ps [41]. Dans cet article, le temps de relaxation et le potentiel chimique que nous avons définis sont suffisamment prudents pour garantir la fiabilité de notre étude numérique.

Résultats et discussion

Lorsque l'onde SPP traverse la nanocavité en forme de U couplée latéralement représentée sur la figure 1a, l'énergie est couplée dans la nanocavité. Une vallée de transmission profonde est obtenue à la longueur d'onde de résonance en raison de l'interférence destructive entre l'onde incidente et la puissance échappée de la nanocavité [12, 13]. La figure 1b trace le spectre de transmission d'une nanocavité en forme de U directement couplée à un guide d'ondes de bus plasmonique avec τ = 1 ps, μ _c1 = 0.3 eV, et μ _c2 =0,9 eV. Un creux prononcé avec une transmittance inférieure à 0,1 est obtenu à la longueur d'onde de résonance de 2437 nm. L'encart de la figure 1b montre la distribution du champ électrique correspondant à la longueur d'onde de résonance, où l'on peut voir que presque aucun SPP ne se propage à travers le guide d'ondes plasmonique. La figure 2a affiche les spectres de transmittance avec un temps de relaxation varié τ =0,6, 0,8 et 1 ps, où l'on peut voir qu'un contraste de transmission plus élevé est obtenu lorsque le temps de relaxation augmente. Ceci est attribué à la réduction de l'absorption ohmique des plasmons lorsque le temps de relaxation de la quantité de mouvement électronique augmente [39]. La transmittance calculée d'un système de guide d'ondes couplé à une nanocavité en forme de U pour différents potentiels chimiques μ _c2 est présenté sur la figure 2b. Le temps de relaxation τ et potentiel chimique μ _c1 sont constamment maintenus à 1 ps et 0,3 eV respectivement. On peut voir que les emplacements des creux sont réglés dynamiquement via le potentiel chimique varié de la nanocavité et du guide d'ondes du bus. Les longueurs d'onde centrales des creux sont de 2455, 2445 et 2437 nm avec μ _c2 = 0,89, 0,895 et 0,9 eV respectivement.

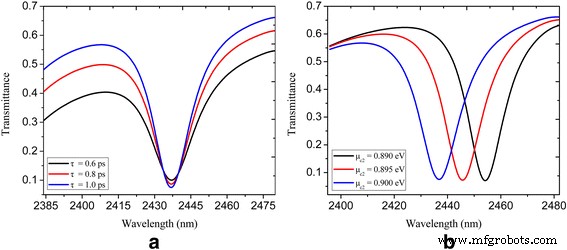
Transmission spectrale d'un système de guide d'ondes couplé à une nanocavité en forme de U illustré à la figure 1 :a avec τ = 0,6, 0,8 et 1 ps ; μ _c1 = 0,3 eV ; et μ _c2 = 0,9 eV ; b avec μ _c2 =  0,89, 0,895 et 0,9 eV ; μ _c1 = 0,3 eV ; et τ = 1 ps

Selon CMT [12, 42, 43], la transmittance spectrale du système supportant un mode de résonance de fréquence ω ₀ peut être écrit comme

où 1/τ _je et 1/τ _e représentent respectivement le taux de décroissance de la perte intrinsèque dans la nanocavité et la puissance s'échappant à travers le guide d'onde du bus plasmonique. Évidemment, la transmission minimale T _min = (1/τ _je ) ² /(1/τ _je + 1/τ _e ) ² peut être atteint lorsque la fréquence de la lumière incidente ω est égal à la fréquence de résonance ω ₀ . Comme le 1/τ _e est bien plus que 1/τ _i , un creux de transmission proche de zéro peut être obtenu, ce qui concorde bien avec les résultats de la simulation.

Afin d'obtenir des effets PIT, nous ajoutons une nanocavité rectangulaire basée sur la nanostructure plasmonique illustrée à la Fig. 1. Une nanostructure plasmonique à base de graphène composée d'un guide d'ondes plasmonique couplé latéralement à des nanocavités en forme de U et rectangulaires est schématiquement illustrée à la Fig. 3a. Il existe un couplage fort entre les deux nanocavités lorsqu'elles sont connectées via le guide d'onde du bus plasmonique. L'interférence destructive entre deux voies d'excitation résonantes liées aux nanocavités en U et rectangulaires génère le phénomène PIT [10, 11]. Comme le montre la figure 3b, un pic de transmission pointu (augmenté de 0,06 à 0,44) est apparu dans la bande interdite de transmission représentée sur la figure 1b, impliquant la formation de la fenêtre PIT. La longueur d'onde centrale de la fenêtre PIT est de 2437 nm, ce qui correspond exactement à l'emplacement de la longueur d'onde centrale du creux de transmission représenté sur la figure 1b. La large résonance de la nanocavité en forme de U est divisée en deux modes de résonance :l'un est décalé vers le bleu tandis que l'autre est décalé vers le rouge [12, 13]. La figure 3c–e affiche les distributions de champ électrique des modes de résonance à 2408, 2437 et 2457 nm respectivement. Nous pouvons voir que la distribution du champ électrique dans les nanocavités est en phase avec la distribution du champ électrique dans les guides d'ondes plasmoniques à 2437 nm, ce qui signifie que la lumière incidente et la lumière s'échappant dans le guide d'ondes plasmonique des nanocavités rencontrent une amélioration cohérente . De plus, les distributions de champ électrique révèlent qu'il y a une antiphase entre les nanocavités et le guide d'onde du bus plasmonique à 2408 et 2457 nm, c'est-à-dire que les conditions de résonance destructrice ont été remplies ce qui entraîne l'inhibition des ondes de transmission [12].

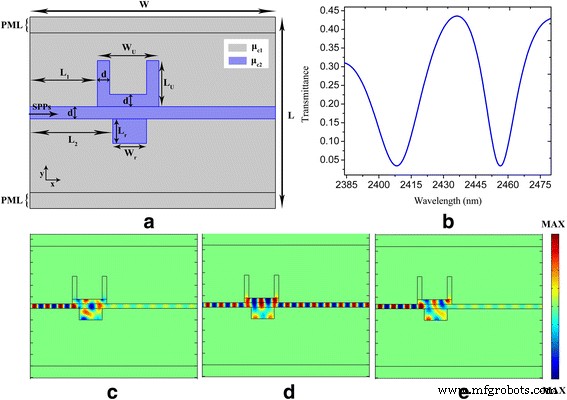
a, b La configuration schématique et les paramètres géométriques du système de guide d'ondes couplé par nanocavité en forme de U et rectangulaire et la transmittance spectrale correspondante respectivement. c –e Champ électrique (E _y ) distribution aux longueurs d'onde de 2408, 2437 et 2457 nm respectivement. Les paramètres sont définis comme W = 800 nm, L = 620 nm, d = 20 nm, W _U = 150 nm, L _U = 120 nm, L ₁ = 220 nm, L ₂ = 250 nm, L _r = 50 nm, W _r = 100 nm, τ = 1 ps, μ _c1 = 0.3 eV, et μ _c2 = 0.9 eV

Nous calculons la transmittance spectrale pour le système de guide d'ondes à bus plasmonique en forme de U et rectangulaire couplé à une nanocavité avec un temps de relaxation varié τ = 0,6, 0,8 et 1 ps, et les résultats sont présentés sur la figure 4a. On peut voir que le contraste de transmission augmente avec l'augmentation du temps de relaxation. De plus, l'accordabilité dynamique de la fenêtre PIT est illustrée sur la figure 4b. Le potentiel chimique μ _c1 est constamment maintenu à 0,3 eV, tandis que μ _c2 est de 0,89, 0,895 et 0,9 eV. Comme le potentiel chimique μ _c2 augmente, le pic de transmission (aux longueurs d'onde de 2452, 2445 et 2437 nm) dans la fenêtre PIT est évidemment décalé vers le bleu. En conséquence, l'effet PIT accordable dynamiquement est réalisé dans notre nanostructure proposée en modifiant le potentiel chimique des nanocavités et du guide d'ondes du bus plasmonique.

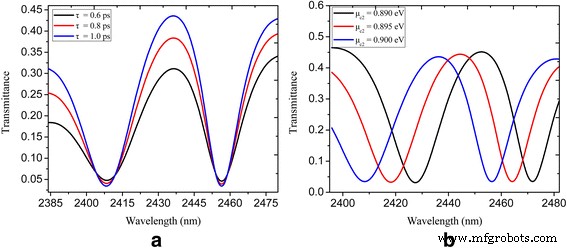
La transmittance spectrale du système de guide d'ondes couplé par nanocavité en forme de U et rectangulaire illustré à la figure 3 :a avec τ = 0,6, 0,8 et 1 ps ; b avec μ _c2 = 0,89, 0,895 et 0,9 eV

Pour étudier comment les paramètres géométriques influencent le phénomène PIT, nous avons modifié l'emplacement de la nanocavité rectangulaire. La figure 5a montre la transmittance spectrale du système de guide d'ondes de bus plasmonique couplé à une nanocavité en forme de U et rectangulaire, où l'on voit que le pic de transmission est devenu plus élevé (passé de 0,44 à 0,52) et que la fenêtre PIT s'élargit avec L ₂ augmentant pour une certaine plage, ce qui est attribué à l'intensification de la force de couplage entre les deux nanocavités [11, 28]. En outre, nous constatons que la diminution de la largeur de la nanocavité rectangulaire peut conduire à un pic de transmission plus élevé (augmenté de 0,44 à 0,48), comme le montre la figure 5b. Cela offre une autre option pour régler la fenêtre PIT. Le facteur de qualité (facteur Q) des fenêtres PIT est défini comme λ ₀ /∆λ , où λ ₀ et ∆λ sont la longueur d'onde de crête de transmission et la pleine largeur à mi-hauteur (FWHM). Dans notre nanostructure plasmonique proposée, une FWHM inférieure à 30 nm et un facteur Q d'environ 80 sont obtenus, ce qui est beaucoup plus étroit et supérieur que les homologues du PIT à base de graphène proposés dans les références susmentionnées [28, 29].

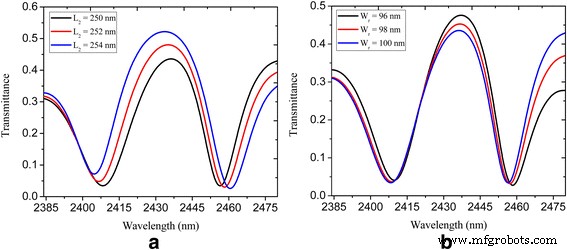
Transmission spectrale du système de guide d'ondes couplé par nanocavité en forme de U et rectangulaire illustré à la Fig. 3 :a avec L ₂ = 250, 252 et 254 nm; b avec W _r = 96, 98 et 100 nm

Conformément au CMT, la transmittance dans notre nanostructure plasmonique est exprimée par [12, 42]

où γ et β représentent respectivement le coefficient de couplage entre les deux nanocavités et le coefficient de couplage entre les nanocavités et le guide d'onde du bus plasmonique. Nous pouvons constater que la fenêtre PIT peut être obtenue lorsque les fréquences de résonance de la nanocavité en forme de U ω _U et la nanocavité rectangulaire ω _r sont à peu près équivalents. Et le pic de transmission correspondant est |( γ + 1)/(β + γ + 1)| ² .

Sur la base de la structure représentée sur la figure 3a, nous construisons le capteur d'indice de réfraction, qui est réalisé en modifiant la permittivité relative dans l'équation. 1. La figure 6a illustre la transmittance spectrale avec différents indices de réfraction n , qui fait référence à l'indice de réfraction du matériau sous-détecté. On peut voir que les longueurs d'onde pic/dip1/dip2 passent de 2437,3 à 2457,3 nm/2410,3 à 2432,4 nm/2457,3 à 2474,9 nm lorsque l'indice de réfraction n varie de 1 à 1,06. Comme l'indice de réfraction n augmente, le pic de transmission et les creux présentent un décalage vers le rouge. La sensibilité de détection du capteur d'indice de réfraction, définie comme le décalage de la longueur d'onde pic/dip1/dip2 par unité de variations de l'indice de réfraction dλ/dn est respectivement de 333,3, 368,3 et 293,3 nm/RIU. La figure 6b montre les pics et les creux de la transmittance spectrale avec l'indice de réfraction n variant de 1 à 1,19, où l'on peut voir la relation approximativement linéaire des longueurs d'onde pic/creux par rapport à l'indice de réfraction n .

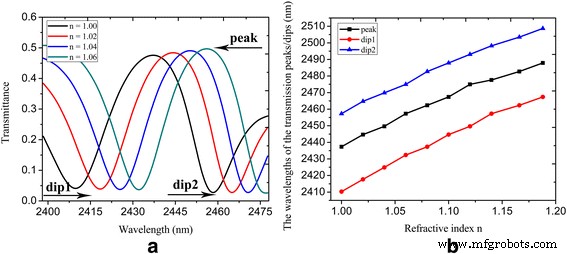
un La transmittance spectrale avec indice de réfraction n = 1, 1,02, 1,04 et 1,06 ; b les longueurs d'onde crête/creux de la transmittance spectrale en fonction de l'indice de réfraction n . Les paramètres sont définis comme W = 800 nm, L = 620 nm, d = 20 nm, W _U = 150 nm, L _U = 120 nm, L ₁ = 220 nm, L ₂ = 250 nm, L _r = 50 nm, W _r = 96 nm, τ = 1 ps, μ _c1 = 0.3 eV, et μ _c2 = 0.9 eV

Il est bien connu que le phénomène PIT s'accompagne de l'effet de lumière lente causé par la forte dispersion [13, 29]. L'effet de lumière lente peut être caractérisé par le retard de groupe exprimé par τ _g = ∂φ (ω )/∂ ω où φ (ω ) est le déphasage effectif du spectre de transmission. Sur la figure 7, nous traçons les retards de groupe dans la fenêtre PIT à différents potentiels chimiques μ _c2 . Au voisinage du pic de transmission PIT, il offre de grands retards de groupe positifs indiquant l'effet de lumière lente. Les longueurs d'onde de crête du système PIT à μ _c2 = 0,89, 0,895 et 0,9 eV sont respectivement de 2449,7, 2442,3 et 2434,7 nm, et les retards de groupe correspondants sont respectivement de 0,99, 1,1 et 1,02 ps. Ainsi, l'effet de lumière lente est réglé efficacement en modifiant le potentiel chimique des nanocavités et du guide d'onde du bus plasmonique. Il convient également de souligner qu'il s'agit d'un article de preuve de concept. En réalité, la structure proposée devrait reposer sur le substrat, où l'indice de réfraction est plus grand que l'air, et la réponse en fréquence se déplacerait en conséquence. Aussi, le confinement du plasmon est plus élevé, s'accompagnant de l'augmentation de la perte, ce qui se traduit par la diminution de la valeur crête de la fenêtre de transparence dans le spectre de transmission. Cependant, le principe est identique au cas suspendu.

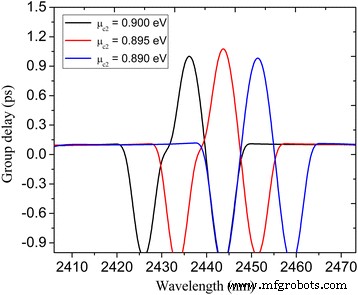
Les retards de groupe versus le potentiel chimique μ _c2 pour le système PIT au graphène illustré à la Fig. 3a. Les autres paramètres sont définis comme W = 800 nm, L = 620 nm, d = 20 nm, W _U = 150 nm, L _U = 120 nm, L ₁ = 220 nm, L ₂ = 254 nm, L _r = 50 nm, W _r = 96 nm, τ = 1 ps, μ _c1 = 0.3 eV

Conclusions

En conclusion, des effets PIT accordables dynamiquement dans une nanostructure plasmonique à base de graphène composée d'un guide d'ondes de bus plasmonique couplé latéralement à des nanocavités en forme de U et rectangulaires ont été proposés et modélisés en utilisant la méthode des éléments finis. L'accordabilité dynamique des fenêtres PIT est obtenue en modifiant le potentiel chimique des nanocavités et du guide d'onde du bus plasmonique. De plus, la fenêtre PIT peut être réglée dynamiquement en ajustant les paramètres géométriques de la nanostructure, tels que l'emplacement et la largeur de la nanocavité rectangulaire. Par rapport aux résonateurs annulaires conventionnels [24, 25], nos résonateurs asymétriques en forme de U et rectangulaires proposés offrent une force de couplage plus forte entre les résonateurs et le guide d'ondes du bus, ce qui entraîne en outre un effet PIT plus fort. D'autre part, contrairement à d'autres guides d'ondes nanoruban rapportés, nos structures sont formées par la variation locale du potentiel chimique sur la monocouche de graphène identique, ce qui facilite l'intégration avec d'autres composants fonctionnels sur la même plate-forme matérielle. De plus, cette nanostructure plasmonique peut être utilisée comme capteur d'indice de réfraction avec une sensibilité de détection élevée. Et l'effet de lumière lente avec un grand retard de groupe est également réalisé dans le système PIT. La nanostructure proposée ouvre une nouvelle voie vers la réalisation de dispositifs nanophotoniques intégrés sur puce à base de graphène.

Abréviations

CMT :

Théorie des modes couplés

EIT :

Transparence induite électromagnétiquement

FEM :

Méthode des éléments finis

PIT :

Transparence induite par le plasmon

RIU :

Unité d'indice de réfraction

SPP :

Polaritons de plasmons de surface