Structure électronique dépendante du spin et de la vallée dans le silicium sous potentiels périodiques

Contexte

Les matériaux Dirac bidimensionnels (2D) avec des structures en réseau hexagonal sont largement explorés depuis la découverte du graphène, tels que le silicène [1, 2], les dichalcogénures de métaux de transition [3, 4] et le phosphorène [5]. Bien que le graphène possède de nombreuses propriétés particulières, son application est limitée par la bande interdite nulle et la faible interaction spin-orbite (SOI). Récemment, un analogue de silicium du graphène, le silicène, a été fabriqué par croissance épitaxiale [6–10], et sa stabilité a été prédite par des études théoriques [11, 12]. Le graphène et le silicène ont des structures de bandes similaires autour de K et K ^′ vallées, et les spectres de basse énergie des deux sont décrits par l'équation relativiste de Dirac [13]. Contrairement au graphène, le silicène a un fort SOI intrinsèque et une structure en boucle. Le SOI fort pourrait ouvrir une brèche aux points de Dirac [13, 14] et conduire à un couplage entre les degrés de liberté de spin et de vallée. La structure flambée permet de contrôler la bande interdite par un champ électrique externe perpendiculaire à la feuille de silice [14-16]. De plus, le silicène présente l'avantage d'être plus compatible avec la technologie électronique existante à base de silicium. Ces caractéristiques font du silicène un excellent matériau pour la nanoélectronique de nouvelle génération. En particulier, un transistor à effet de champ au silicène à température ambiante a été fabriqué avec succès par un processus de fabrication-transfert de croissance dans l'expérience [17].

La découverte des matériaux Dirac 2D offre de nouvelles opportunités pour explorer le contrôle quantique de la vallée. Les deux vallées inéquivalentes K et K ^′ dans la première zone de Brillouin pourrait être considérée comme un degré de liberté supplémentaire en plus de la charge et du spin pour l'information quantique et le calcul quantique [18–20]. Par exemple, le degré de liberté de vallée peut être incorporé pour étendre un qubit de spin d'électron à un qubit de vallée de spin [18]. Par conséquent, la valleytronics qui vise à générer, détecter et manipuler le pseudospin de la vallée a suscité un intérêt considérable. Dans le graphène, divers schémas pour obtenir une polarisation de vallée ont été proposés en utilisant des modes de bord uniques [21, 22], un effet de déformation trigonale [23], des défauts de ligne topologiques [24, 25], une contrainte [26, 27] et des portes électrostatiques [28]. Par rapport au graphène, le silicène a un avantage significatif dans l'étude du pseudospin de la vallée. On constate que le silicène présente une riche variété de phases topologiques et de nombres de Chern sous la modulation de différents champs externes [13, 16, 29, 30]. En présence de champ électrique E _z et champ d'échange h , Ezawa a exploré le diagramme de phase dans le E _z −h plan qui est caractérisé par les indices de spin et de vallée [16]. En considérant en outre le Rashba SOI, un état Hall anormal quantique polarisé dans la vallée est prédit dans le silicène en raison de la transition de phase topologique [31]. Sur la base de la transition d'état, un filtre de spin à base de silicène avec près de 100 % de polarisation de spin est proposé, qui est robuste contre le désordre faible [32]. Yokoyama a étudié le transport balistique à travers une jonction de silice ferromagnétique (FM) et a démontré un courant de spin et de vallée polarisé contrôlable [33]. Dans les dichalcogénures de métaux de transition avec une symétrie d'inversion brisée, la division de spin des bandes de valence résultant du SOI intrinsèque est opposée aux deux vallées en raison d'une symétrie de retournement temporel [3, 34, 35]. La symétrie d'inversion brisée pourrait entraîner une règle de sélection optique dépendante de la vallée, qui peut être utilisée pour exciter sélectivement les porteurs dans le K ou K ^′ vallée via une lumière polarisée circulairement à droite ou à gauche, respectivement [3, 34]. Expérimentalement, le signal de polarisation de vallée a été sondé par des mesures optiques [36, 37] et de transport [38, 39]. Un effet Hall de vallée non local géant a été observé dans du graphène bicouche soumis à un champ électrique de grille à rupture de symétrie, et le signal non local persiste jusqu'à la température ambiante [38]. Une revue récente de valleytronics dans les matériaux Dirac 2D est fournie dans la réf. [40].

Le super-réseau est une méthode efficace d'ingénierie de la structure électronique dans les semi-conducteurs et les matériaux 2D [41]. Des motifs de super-réseau à l'échelle nanométrique peuvent naturellement apparaître dans l'expérience lorsque du graphène ou du silicène est placé sur des substrats métalliques [42, 43]. Un super-réseau dans le graphène pourrait conduire à une renormalisation de la vitesse de Fermi anisotrope [44] et à la génération de nouveaux points de Dirac dans le spectre [45-47] en raison de la nature chirale, qui ont été observées expérimentalement [43, 48, 49]. Dans les super-réseaux de silice à champ électrique E _z et champ d'échange h , les dégénérescences de spin et de vallée sont toutes deux levées. Il est confirmé que la structure des minibandes et les minigaps causés par les super-réseaux dépendent des indices de spin et de vallée [50]. De plus, les polarisations de spin et de vallée pourraient être renforcées par les super-réseaux de silice [51]. Tout comme le graphène, de nombreuses nouvelles structures électroniques sont attendues dans les super-réseaux de silice. Cependant, les travaux sur les super-réseaux silicènes sont très peu nombreux [50, 51]. Dans cet article, nous discutons en détail un aspect complémentaire, à savoir la structure de bande dépendante du spin et de la vallée et la propriété de transport du silicène. Nous avons constaté que les indices de spin et de vallée ont des impacts différents sur les points de Dirac supplémentaires et la vitesse anisotrope qui peuvent être ajustés par les paramètres structurels. La vitesse est fortement supprimée en raison du champ électrique et du champ d'échange. Une polarisation de spin et de vallée remarquable est obtenue, qui peut être grandement améliorée par le trouble.

L'article est organisé de la manière suivante. Dans la section « Méthodes », nous présentons le formalisme théorique et la relation de dispersion. Les résultats numériques sur la structure de bande, les transmissions polarisées en spin et vallée sont présentés dans la section « Résultats et discussions ». Enfin, nous concluons par un résumé dans la section « Conclusions ».

Méthodes

Dans l'approximation monoparticule, la structure électronique du silicène au voisinage des points de Dirac obéit à un hamiltonien de Dirac effectif. Le système considéré est un super-réseau de silice unidimensionnel formé par une série de barrières potentielles locales U , échangez les champs h , et champ électrique perpendiculaire E _z . U , h , et E _z ne sont présents que dans les régions barrières avec une largeur de barrière d _b , tandis que U =h =E _z =0 dans les régions de puits avec une largeur de puits d _w , comme le montre la figure 1. Le super-réseau de type Kronig-Penney ne varie que le long de x direction, et la longueur d'une unité est d =d _b +d _w . Un modèle similaire a été discuté dans les réfs. [51, 52], qui se concentrent principalement sur le transport thermoélectrique et électronique plutôt que sur la structure de bande et l'effet de désordre étudiés dans ce travail. Expérimentalement, U peut être produit par les portes métalliques et h peut être produit par l'effet de proximité magnétique avec les isolants FM EuO [33], qui sont déposés périodiquement au-dessus de la couche de silice (voir Fig. 1). Le champ électrique E _z appliqué perpendiculairement au silicène peut induire un potentiel de sous-réseau décalé Δ _z =ℓ E _z , avec 2ℓ ≈0.46Å la séparation verticale de A et B sites des deux sous-réseaux en raison de la structure déformée [16]. Par conséquent, les états électroniques peuvent être décrits par l'hamiltonien,

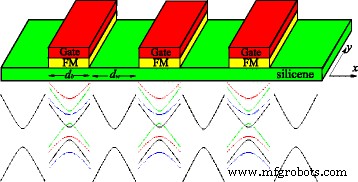
En haut :schéma des super-réseaux silicènes. Les isolants FM, tels que EuO et EuS, au sommet du silicène induisent les champs d'échange dans le silicène, comme proposé pour le graphène [53]. Les grilles métalliques sur le dessus des isolateurs FM contrôlent localement le niveau de Fermi. En bas :schéma du spectre énergétique en silicène avec et sans champs extérieurs

Δ _{η σ} =Δ _z −η σ λ _SO décrit la bande interdite pour différents indices de spin et de vallée, qui peut être contrôlé par le potentiel échelonné Δ _z et le SOI λ _SO . U _σ =U −σ h est le potentiel effectif pour différents indices de spin. η =±1 désigne le K et K ^′ vallées. σ =±1 désigne les états de montée et de descente. v _F est la vitesse de Fermi. Dans le silicène, les effets Rashba intrinsèques et extrinsèques sont très faibles et peuvent être négligés [15].

En raison de l'invariance translationnelle le long du y direction, le vecteur d'onde transverse k _y est conservé. La fonction d'onde pour la vallée η et fais tourner σ dans chaque région a la forme Ψ (x ,y )=ψ (x )e ^iky _y avec

Dans les régions barrières, ε _{η σ} =ε _b =(E −T _σ )+Δ _{η σ} et le x composante du vecteur d'onde \( q_{\eta \sigma } =q_{b} =\sqrt {(E - U_{\sigma })^{2} - \Delta ^{2}_{\eta \sigma } - (\hbar v_{F} k_{y})^{2}} / \hbar v_{F} \). Dans les régions de puits, ε _{η σ} =ε _w =E −η σ λ _SO et \( q_{\eta \sigma } =q_{w} =\sqrt {E^{2} - \lambda _{SO}^{2} - (\hbar v_{F} k_{y})^{ 2}} / \hbar v_{F} \). k _± =q _{η σ} ±i η k _y . La probabilité de transmission T _{η σ} peut être calculé en utilisant la technique de la matrice de transfert. La conductance normalisée pour un spin particulier dans une vallée particulière à température nulle est donnée par

où θ est l'angle incident par rapport au x direction. Les conductances résolues en spin et vallée sont définies comme \(G_{\uparrow (\downarrow)} =\left (G_{K \uparrow (\downarrow)} + G_{K^{\prime } \uparrow (\downarrow )} \right) / 2 \) et \(G_{K (K^{\prime })} =\left (G_{K (K^{\prime }) \uparrow } + G_{K (K^{ \prime }) \downarrow } \right) / 2\), respectivement. Ensuite, nous introduisons la polarisation de spin P _s et polarisation de vallée P _v :

Sur la base du théorème de Bloch et de la condition de continuité des fonctions d'onde, la relation de dispersion E (k _x ) pour les électrons de spin-up et de spin-down près du K et K ^′ les vallées peuvent être calculées,

et k _x est le nombre d'onde de Bloch. Afin de simplifier le calcul, les unités sans dimension sont introduites :\(E \rightarrow E d / \hbar v_{F}\), \(U \rightarrow U d / \hbar v_{F}\), \(\ lambda _{SO} \rightarrow \lambda _{SO} d / \hbar v_{F}\), \(\Delta _{z} \rightarrow \Delta _{z} d / \hbar v_{F}\) , \(h \rightarrow hd / \hbar v_{F}\), k _y →k _y d , k _x →k _x d , d _w →d _w /d , et d _b →d _b /d . Notez qu'à Δ _z =λ _SO =h =0, Éq. (6) est réduit à celui trouvé pour le graphène sans lacune dans un potentiel périodique, où le spin et la vallée sont dégénérés [44-47]. De l'éq. (6), nous pouvons voir ce champ d'échange h seul pourrait induire la scission du spin, tandis que la vallée maintient la dégénérescence. Cependant, la dégénérescence de la vallée peut être levée par le champ électrique E _z avec l'aide du SOI λ _SO . Ainsi, une combinaison du champ d'échange et du champ électrique pourrait soulever les dégénérescences de spin et de vallée [16, 31-33], comme le montre la Fig. 1. Dans le système proposé, les électrons avec des spins différents à proximité de différentes vallées présenteraient différentes bandes structures et caractéristiques de transport.

Résultats et discussions

Dans cette section, nous utiliserons les équations ci-dessus pour calculer les structures de bandes et les propriétés de transport pour différents indices de spin et de vallée dans les super-réseaux de silice. Les largeurs des barrières et des puits sont supposées être les mêmes dans ce qui suit. Les résultats pour le cas avec des largeurs de puits et de barrière inégales (d _b ≠d _w ) sont similaires à ceux du graphène sans lacune [47]. Certains paramètres sont définis comme d _b =d _w =50 nm et λ _SO =3,9 meV dans le silicène, sauf indication contraire. Nous nous concentrerons sur les deux premières minibandes (les minibandes de valence et de conduction les plus basses) proches du niveau de Fermi.

Structure de bande dépendante de la rotation et de la vallée

Premièrement, l'effet du potentiel U sur les minibandes est représenté sur la Fig. 2. Afin de discuter simultanément du cas avec intervalle et du cas sans intervalle de bandes d'énergie, nous définissons Δ _z =7.8 meV=2λ _SO . En l'absence de potentiel (U =0), l'électron de spin-up près de K vallée (K ↑ électron) et électron de spin-down près de K ^′ vallée (K ^′ ↓ électron) sont sans espace (voir Fig. 2 (a1, a4)), tandis que l'électron de spin-down près de K vallée (K ↓ électron) et électron de spin-up près de K ^′ vallée (K ^′ ↑ électron) ont un grand écart (voir Fig. 2 (a2, a3)). Les minibandes de spin-up (ou spin-down) se déplacent vers la plage d'énergie négative (ou positive) de E =0 par h , en raison du potentiel effectif U _σ =U −σ h . Les structures de bande de K ↑ (ou K ↓ ) électron et K ^′ ↓ (ou K ^′ ↑ ) symétrie du miroir à électrons présents par rapport à E =0, conforme à l'équation. (6). Cependant, cette symétrie miroir est détruite en présence de U . Observable, comme U augmente, des points Dirac supplémentaires apparaissent, dont le nombre augmente entre-temps. Les points de Dirac supplémentaires peuvent être démontrés par la chiralité des fonctions d'onde dans leur voisinage [46]. Les caractéristiques des points de Dirac dans le système silicène dépendent fortement des degrés de liberté de rotation et de vallée, comme le montre la figure 2. Par exemple, à U =135 meV sur la figure 2 (d1–d4) pour K ↑ , K ↓ , K ^′ ↑ et K ^′ ↓ électrons, les nombres de points de Dirac sont 5, 6, 4 et 7, respectivement. Pour des valeurs spécifiques de U , comme U =40,66 meV pour K ↓ électron (voir Fig. 2 (b2)) et U =100,63 meV pour K ^′ ↑ électron (voir Fig. 2 (c3)), un nouveau point de Dirac peut être généré à k _y =0, et il se divisera en une paire qui se déplacera dans des directions opposées en s'éloignant du k _y =0 point mais en gardant toujours k _x =0, comme U augmente encore. En conséquence, les bandes interdites pour K ↓ et K ^′ ↑ les électrons sont fermés (voir Fig. 2 (b2, c3)), et le système à espacement devient sans espace. Afin de trouver la valeur critique de U , nous définissons d _b =d _w et k _x =0. De manière analogue à la règle du graphène sans lacune [47], en tenant compte du théorème des fonctions implicites, on peut conclure que les vecteurs d'onde longitudinaux aux nouveaux points de Dirac satisfont q _b =q _w quand

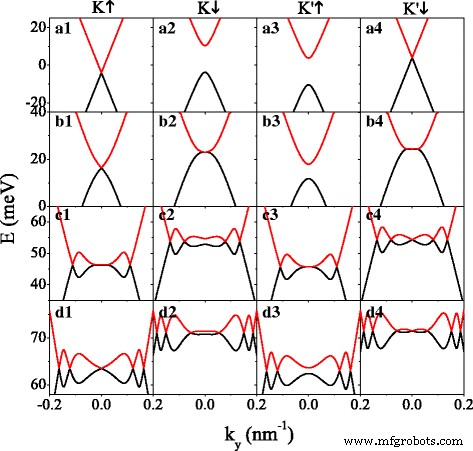
Spectre énergétique versus k _y pour plusieurs valeurs différentes de potentiel U . (a1–a4) U =0; (b1–b4) U =40,66 meV ; (c1–c4) U =100,63 meV ; (d1–d4) U =135,0 meV. Les valeurs des paramètres sont h =8.0 meV, Δ _z =7.8 meV, et k _x =0

Pour K ↑ et K ^′ ↓ électrons avec η σ =1, quand Δ _z =2λ _SO , Éq. (7) peut réduire à

En conséquence, l'éq. (6) se transforme en

qui est satisfait quand \(\left (\epsilon _{b}^{2} + \epsilon _{w}^{2}\right) q_{w}^{2} + (\epsilon _{b} - \epsilon _{w})^{2} k^{2}_{y} =-2 \epsilon _{w} \epsilon _{b} q_{w}^{2}\) ou q _w d =2n π (n est un entier positif). Basé sur l'éq. (8), nous avons ε _b =−ε _w , et donc la première égalité n'est remplie que si k _{y 0} =0 pour K ↑ et K ^′ ↓ électrons à Δ _z =2λ _SO , correspondant au point de Dirac d'origine. Les solutions de q _w d =2n π avoir la forme

Lorsque \(\sqrt {E_{0}^{2}-\lambda _{SO}^{2}}d / 2\pi \hbar v_{F} \geq n\), k _{y 0} est réel, et les nouveaux points de Dirac apparaîtront qui sont exactement situés à (E ₀ ,k _{y 0} ). Aux faibles valeurs de U , k _{y 0} est imaginaire, et il n'y a pas de solution pour n , ce qui signifie pas de points Dirac supplémentaires. Les points Dirac n'apparaissent qu'après une valeur critique de U , comme U =40,66 meV pour K ↓ électrons sur la figure 2 (b2), correspondant à n =1. Selon l'éq. (10), Le nombre de points Dirac N _D peut être obtenu. Quand Δ _z =2λ _SO ,

pour K ↑ et K ^′ ↓ électrons, tandis que

pour K ↓ et K ^′ ↑ électrons, où [...] désigne une partie entière. Notez qu'à la valeur critique de U , comme U =40,66 meV et 100,63 meV, le nombre de points Dirac est N _D =2n -1 pour K ↓ et K ^′ ↑ électrons (voir Fig. 2 (b2, c3)).

Les équations (7) et (10) manifestent que les positions et les nombres de points de Dirac pourraient être ajustés par le champ électrique E _z et champ d'échange h . La figure 3 présente le nombre de points Dirac N _D en fonction de U pour différentes valeurs de E _z et h . Quand Δ _z =7,8 meV sur la figure 3a, avec un U croissant , N _D pour K ↑ et K ^′ ↓ électrons augmente sous la forme d'un nombre impair, conforme à l'équation. (11). N _D pour K ↓ et K ^′ ↑ électrons augmente sous la forme d'un nombre pair, conforme à l'équation. (12), sauf pour N _D à la valeur critique. La comparaison entre les Fig. 3a et b indique que comme h augmente, la valeur critique pour l'électron de spin-down (ou spin-up) diminue (ou augmente) progressivement. Quand Δ _z =15 meV≠2λ _SO dans la figure 3c, N _D pour tous les électrons augmente sous forme de nombre pair, sauf pour N _D à la valeur critique. Décidément, les valeurs critiques de U sont différents pour les électrons avec des spins et des vallées différents. Les points de Dirac pourraient être contrôlés par une modulation conjointe des paramètres U , E _z , et h .

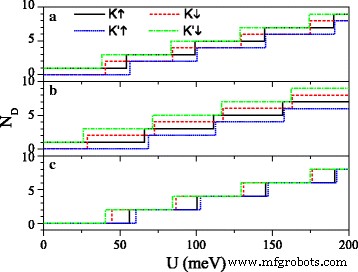
Nombre de points Dirac N _D par rapport au potentiel U . (un ) h =8.0 meV et Δ _z =7,8 meV ; (b ) h =20,0 meV et Δ _z =7,8 meV ; (c ) h =8,0 meV et Δ _z =15,0 meV

Le potentiel U et largeur de barrière d _b pourrait être utilisé pour réguler la bande interdite, comme illustré à la Fig. 4. Les lacunes pour K ↑ et K ^′ ↓ les électrons sont petits, tandis que les écarts pour K ↓ et K ^′ ↑ les électrons sont gros en raison de Δ _{η σ} =Δ _z −η σ λ _SO . En tant que U augmente, toutes les minibandes se déplacent progressivement vers la région de haute énergie (voir Fig. 4a), et toutes les bandes interdites affichent une oscillation amortie avec U (voir Fig. 4b). Quand U =σ h , le potentiel effectif est nul et l'écart atteint la valeur maximale. L'écart est comblé à la valeur critique de U , en raison de l'émergence de nouveaux points Dirac. La figure 4c, d illustre la dépendance des minibandes et des bandes interdites par rapport à la largeur de barrière d _b à U =0. En l'absence de champ externe (d _b =0), les minibandes continuent de dégénérer, et l'écart au niveau de Fermi est de 2λ _SO . Avec l'apparition de d _b , la minibande est divisée, où la vallée et le spin deviennent non dégénérés. Les minibandes de K ↑ (ou K ↓ ) et K ^′ ↓ (ou K ^′ ↑ ) les électrons gardent une symétrie miroir autour de E =0 (voir Fig. 4c). Comme d _b augmente, les écarts de K ↓ et K ^′ ↑ les électrons s'élargissent progressivement. Les lacunes de K ↑ et K ^′ ↓ les électrons diminuent jusqu'à zéro lorsque d _b satisfait d _b /d _w =λ _SO /Δ _z , et ensuite augmenter avec d _b (voir Fig. 4d). Les largeurs d'intervalle approchent de la saturation avec l'augmentation supplémentaire de d _b . De plus, la largeur de la minibande est réduite comme d _b augmente (non représenté sur la figure), en raison du moindre couplage d'états propres. L'effet du champ électrique sur la bande interdite est analogue à celui de l'étude précédente [50].

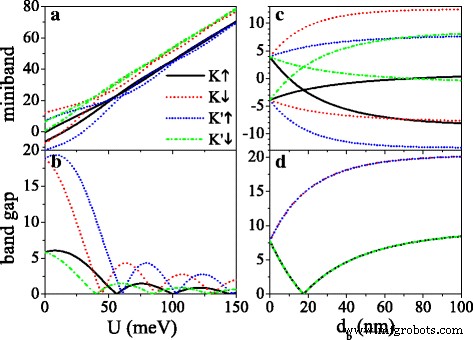
(un ) Minibandes proches du niveau de Fermi et (b ) leurs bandes interdites au point de Dirac d'origine par rapport au potentiel U , à d _b =d _w =50 nm. (c ) Minibandes proches du niveau de Fermi et (d ) leurs bandes interdites au point de Dirac d'origine par rapport à d _b , à U =0 et d _w =50 nm. Les valeurs des autres paramètres sont h =8.0 meV, Δ _z =15,0 meV, et k _x =k _y =0

La vitesse de groupe dépend fortement des indices de spin et de vallée, comme le montre la figure 5. Les composants (v _x ,v _y ) de la vitesse peut être défini comme

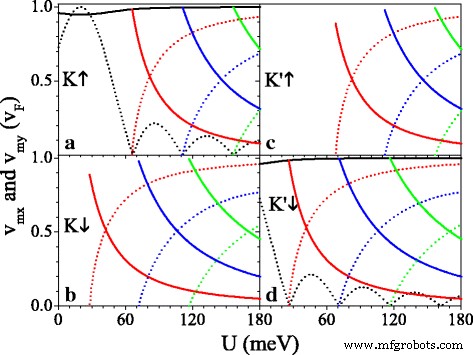
(un –d ) Vitesse par rapport au potentiel U , et les paramètres sont définis comme h =20,0 meV et Δ _z =7,8 meV. Les courbes pleines noires, rouges, bleues et vertes sont les vitesses v _0x , v _1x , v _2x , et v _3x , respectivement. Les courbes en pointillés noir, rouge, bleu et vert sont les vitesses v _0y , v _1y , v _2y , et v _3y , respectivement

La figure 5 présente les composantes de la vitesse v _mx et v _mon en unités de v _F au point de Dirac d'origine (m =0) et de nouveaux points Dirac (m =1,2,3). On peut voir cela comme U augmente, v _0y oscille de manière décomposée et v _0x v _F n'est pratiquement pas affecté (voir Fig. 5a, d). A la valeur critique de U où émergent les nouveaux points de Dirac, v _mx v _F mais v _0y =v _mon =0, indiquant un comportement de collimation le long du k _x direction pour des spins et des vallées spécifiques. Quand U dépasse la valeur critique et augmente encore, v _mon passer à v _F mais v _mx diminuer progressivement jusqu'à zéro. L'effet du potentiel périodique est fortement anisotrope, en raison de la nature chirale. Les caractéristiques de la vitesse anisotrope sont diverses pour différents spins et vallées en raison de l'écart Δ _{η σ} et le potentiel U _σ , qui peut être commandé en utilisant U . Prendre U =20 meV par exemple, v _0y =v _F pour K ↑ électron est beaucoup plus grand que v _0y =0.16v _F pour K ^′ ↓ électron, et pas de v _0y pour K ↓ et K ^′ ↑ électrons en raison de la bande interdite. v _mx (ou v _mon ) pour l'électron de spin-up est toujours plus grand (ou moins) que celui pour l'électron de spin-down dans la même vallée. Notamment, la figure 5 implique également que pour une petite valeur de U , v _0x , v _0y , et v _mx sont inférieurs à v _F en raison de Δ _z et h , autre que le système gapless [44]. Par exemple, v _1x =0.98v _F , 0,89v _F , 0,89v _F , et 0.98v _F pour K ↑ , K ↓ , K ^′ ↑ et K ^′ ↓ électrons, respectivement, lorsque le point de Dirac apparaît. Afin d'éclairer l'influence de Δ _z et h sur la vitesse de groupe, la Fig. 6 montre les vitesses (v _0x ,v _0y ) en fonction de (a) Δ _z et (b) h pour K ↑ électron. À partir de la figure 6a, nous pouvons clairement voir que v _0x est décroissant de façon monotone avec Δ _z tandis que v _0y est insensible au changement de Δ _z . Au contraire, v _0x est désensibilisé à h , tandis que v _0y augmente jusqu'à la valeur maximale v _0y =v _F à h =σ U puis diminue avec h . Les résultats indiquent que la vitesse de groupe peut être supprimée par Δ _z et h en silicène.

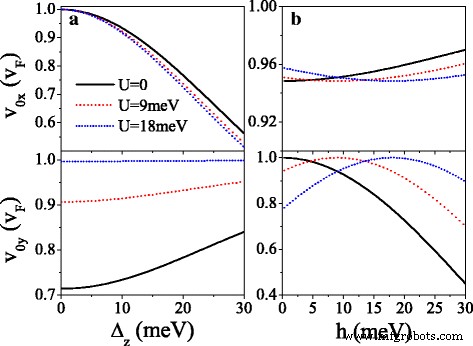
Vitesses v _0x et v _0y contre (a ) Δ _z et (b ) h , pour K ↑ électron. (un ) h =20,0 meV et λ _SO =Δ _z /2. (b ) Δ _z =7.8 meV

Transport polarisé en rotation et en vallée

La structure de bande dépendante du spin et de la vallée se reflète dans la propriété de transport et fournit un guide dans le contrôle du transport. Dans cette section, nous discutons des propriétés du transport polarisé en spin et en vallée à travers un super-réseau silicène fini. La figure 7 montre la probabilité de transmission T _{η σ} pour (a, c) K ↑ et (b, d) K ↓ électrons, et le nombre de période n =10. Les courbes en pointillés rouges sont les mini-bandes, qui sont également les frontières des différents états électroniques qui décident de la transmission. Nous pouvons voir que la transmission est restreinte dans la région de la minibande et aucune transmission dans la région de la bande interdite (voir Fig. 7a, b). La distribution de la transmission est symétrique autour de k _y =0 en raison des minibandes symétriques. La caractéristique de résonance de la transmission provient des états de résonance. Il convient de noter que la transmission existe toujours dans la région de l'écart près de k _y =0 en raison de l'effet tunnel des états propres. T _{η σ} au niveau Fermi pour K ↑ et K ↓ les électrons sont représentés sur la Fig. 7c, d), respectivement. On peut clairement voir que de nombreux pics de résonance minces avec T _{η σ} =1 se produisent précisément aux positions des points de Dirac, suggérant une application du système en tant que filtre de spin et vallée.

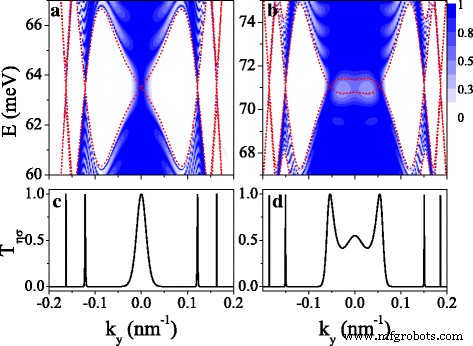
Tracé de contour de la transmission T _{η σ} (E ,k _y ) pour (a ), (c ) K ↑ électron et (b ), (d ) K ↓ électron. Les valeurs des paramètres sont les mêmes que celles de la Fig. 2 (d1–d4), et n =10

La forte dépendance de la structure de bande sur les indices de spin et de vallée est bénéfique pour la réalisation de polarisations de spin et de vallée élevées. La figure 8 présente les minibandes, les conductances G _{η σ} , polarisation de spin P _s , et la polarisation de vallée P _v en fonction du potentiel U . On peut constater que la distribution de la conductance est tout à fait en accord avec la structure de la bande, c'est-à-dire que la conductance (ou écart de conductance) correspond à la minibande (ou écart de bande). Les minibandes pour les électrons de spin-up et de spin-down pourraient être une distribution alternative en ajustant h correctement. Par conséquent, \(G_{K(K^{\prime })\uparrow }\) et \(G_{K(K^{\prime })\downarrow }\) présentent également une distribution alternative, c'est-à-dire \(G_ {K(K^{\prime })\uparrow }\) disparaît presque pour les régions où \(G_{K(K^{\prime })\downarrow }\) est en résonance et vice versa. This result directly leads to a remarkable spin polarization, proposing a switching effect of spin polarization (see Fig. 8a). By changing Δ _z , the minibands and conductances for electrons near K et K ^′ valleys could be controlled, leading to a fully valley-polarized current (see Fig. 8b). Compared with spin polarization, the valley polarization is not perfect enough. However, this drawback could be remedied via the disorder structure of the system, as discussed in the following.

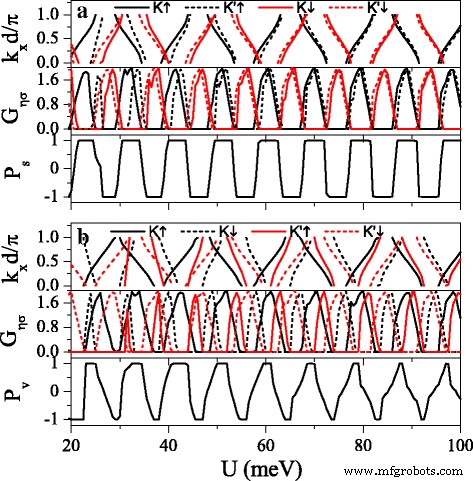
Minibands, conductances G _{η σ} , spin polarization P _s , and valley polarization P _v versus potential U . (un ) Δ _z =4.0 meV. (b ) Δ _z =12.0 meV. Other parameters are set as h =7.0 meV, E =6.0 meV, d _b =d _w =120 nm, and n =10

Figure 9 shows the (a) spin polarization P _s and (b) valley polarization P _v in (U ,h ) space. Interestingly, both P _s and P _v present periodical changes in the considered region, which is not observed in the ferromagnetic silicene junction [33]. Both distributions of P _s and P _v are antisymmetric with respect to h →−h . It is possible to achieve independently a full spin and valley polarization by a proper tuning of the fields U et h . For example, when h =6 meV and U =42 meV, P _s ≈1 and P _v ≈1, meaning that the current is mainly contributed by K ↑ electrons. When h =6 meV and U =44 meV, P _s ≈1 and P _v ≈−1 while P _s ≈−1 and P _v ≈−1 at h =6 meV and U =46 meV. The results demonstrate that a spin and valley polarization can be switched effectively.

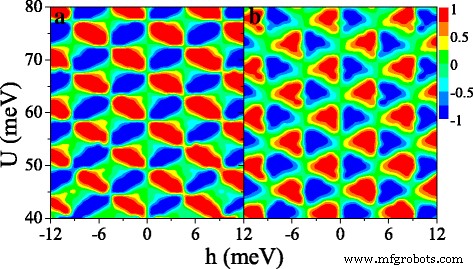
Contour plot of (a ) spin polarization P _s (U ,h ) et (b ) valley polarization P _v (U ,h ), at Δ _z =10.0 meV. The values of other parameters are the same as these in Fig. 8

In experiment, the structural imperfection of the model is unavoidable due to the limitations of the experimental techniques. Therefore, it is necessary to discuss the effect of the disorder on transmission. When the electric field or exchange field presents disorder, the conductance, spin polarization, and valley polarization are shown in Figs. 10 and 11. We set disorder situations of Δ _z et h fluctuate around their mean values, given by 〈Δ _z 〉=Δ _{z 0} and 〈h 〉=h ₀ , respectivement. The fluctuations are given by

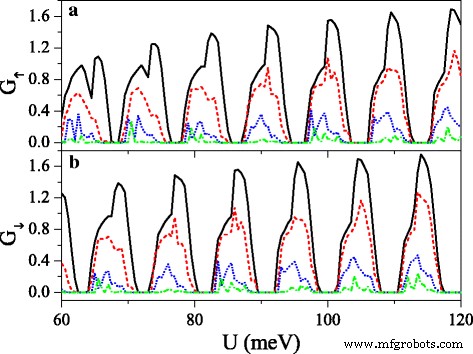
Conductances (a ) G _↑ and (b ) G _↓ versus potential U , when the electric field presents disorder, at n =50 and Δ _{z 0} =20.0 meV. The solid, dashed, dotted, and dash-dotted curves correspond to the disorder strength δ =0.0, 0.1, 0.3, and 0.6, respectively. The values of other parameters are the same as these in Fig. 8

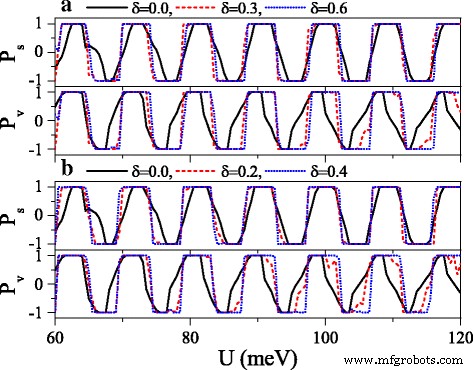
Polarizations P _s and P _v versus potential U when a the electric field or b the exchange field presents disorder. Δ _{z 0} =20.0 meV and h =7.0 meV in (a ). Δ _z =20.0 meV and h ₀ =7.0 meV in (b ). The values of other parameters are the same as these in Fig. 10

where {ζ _i } is a set of uncorrelated random variables or white noise, − 1<ζ _i <1, δ is the disorder strength, and i is the site index. Note that the disorder only takes place in the x direction, and the system is always homogeneous in y direction. Thus, k _y still keeps conservation. Figure 10 exhibits the effect of the disorder of the electric field on the conductances (a) G _↑ and (b) G _↓ . With the presence and increase of the disorder strength δ , both G _↑ et G _↓ are suppressed gradually, and each resonant peak splits into many small peaks. One may find that the conductance range is narrowed while the conductance gap range is broadened. Hence, the allowable (or forbidden) ranges of G _↑ completely fall into the forbidden (or allowable) ranges of G _↓ , giving rise to an excellent spin polarization (see Fig. 11). Furthermore, the positions of conductances and conductance gaps are nearly invariable as δ changes, suggesting that the miniband and band gap are insensitive to the disorder. Note that the disorder effect of the electric field on G _K et G _K ^′ is similar to that observed in Fig. 10. Figure 11 presents the disorder effects of (a) the electric field and (b) the exchange field on polarizations P _s and P _v . Obviously, with the increase of δ , P _s and P _v increase greatly, and the polarization platform is broadened. Thus, a full spin and valley polarization is realized. Comparison between Fig. 11a and b indicates that the disorder effect of exchange field is more prominent. The results demonstrate that the disorder could enhance the spin and valley polarizations compared with the order case, which is an advantage in realistic application.

Conclusions

In summary, we demonstrated detailedly that band structure and transport property of silicene under a periodic field strongly depend on the spin and valley degrees of freedom. The numerical results indicate that electrons with different spins and valleys have various characteristics in Dirac point, bang gap, and group velocity. In particular, owing to the electric field and exchange field, the anisotropic velocity is restrained, which displays a collimation behavior for specific spins and valleys. Therefore, the transmission presents strong spin- and valley-dependent feature, consistent with the band structure, resulting in a significant spin and valley polarizations. In addition, the disorder could greatly enhance the spin and valley polarizations. Finally, we hope these results can be conducive to the potential applications of the spin and valley indices.

Abréviations

2D :

Bidimensionnel

FM:

Ferromagnetic

SOI :

Spin-orbit interaction