Estimation du stockage d'énergie d'un supercondensateur basée sur des équations différentielles fractionnaires

Contexte

À ce jour, les supercondensateurs sont les principaux composants de nombreux appareils et systèmes, par exemple, les systèmes d'alimentation de secours et de récupération d'électricité ainsi que les applications automobiles, les véhicules hybrides et bien d'autres. La capacité d'accumuler des charges sans aucune réaction chimique fait que ces éléments ont un nombre de cycles de charge/décharge des centaines de fois plus élevé que les batteries typiques [1]. De plus, les taux de charge/décharge élevés les rendent efficaces pour les applications dans les systèmes de récupération d'énergie utilisés par exemple dans les transports ou les sources d'énergie renouvelables [2, 3]. Dans toutes ces applications, le paramètre clé est l'information sur la quantité d'énergie accumulée dans le supercondensateur [4, 5]. Malheureusement, la relation bien connue pour les condensateurs typiques qui permet de déterminer l'information, c'est-à-dire (1/2)C U ² , ne peut pas être utilisé [6]. La quantité d'énergie accumulée ne peut pas être déterminée sur la base de la tension aux bornes du condensateur uniquement. La principale raison en est le processus de diffusion associé à la redistribution des charges [1, 7]. C'est pourquoi de nombreux chercheurs ont tenté de déterminer un modèle de supercondensateur qui permettrait d'estimer le comportement d'un système réel. Actuellement, les chercheurs adoptent principalement les combinaisons d'éléments électroniques typiques, par exemple, RC quadripôle ou combinaisons série et parallèle de tels éléments. Cependant, tous ces modèles supposent une relation entre le courant du supercondensateur et la tension à sa borne sous la forme d'une équation différentielle d'ordre entier typique [3–5, 7].

Mais il s'avère que des possibilités complètement nouvelles pour l'estimation de l'énergie dans de tels systèmes peuvent être obtenues par l'application du calcul fractionnaire [8, 9]. Le calcul différentiel-intégral d'ordre non entier a été proposé il y a plus de 300 ans, mais d'importants problèmes de mise en œuvre sont liés à l'avènement des ordinateurs et à leur utilisation dans la modélisation de systèmes dynamiques à temps discret [10-14]. L'application du calcul fractionnaire au problème de l'estimation des paramètres des supercondensateurs n'est pas un problème nouveau. Il existe de nombreuses publications dans ce domaine [15–25]. Les auteurs ont pour tâche d'estimer les paramètres dans les domaines fréquentiel et temporel [26].

Cet article est une version étendue de la présentation de la conférence de l'auteur [27], dans laquelle une approche d'ordre fractionnaire a été brièvement introduite pour estimer l'énergie accumulée dans le supercondensateur.

Une estimation précise des paramètres des supercondensateurs est également de la plus haute importance pour évaluer leur fiabilité [28-31]. Les processus de dégradation permanents à l'intérieur du supercondensateur peuvent modifier la résistance et la capacité série équivalentes. Ainsi, une détermination précise de ces paramètres, basée sur la méthode proposée, permet également d'évaluer avec précision les performances du condensateur.

Cet article commence par quelques préliminaires liés à l'intégration et à la différenciation d'ordre fractionnaire. Ensuite, il présente la méthode d'estimation des paramètres utilisée lors des tests et propose une nouvelle méthode de calcul de l'énergie basée sur le calcul fractionnaire. La section Résultats et discussion présente l'énergie calculée pour divers scénarios et les compare aux valeurs de référence (mesurées). Les conclusions et contributions sont résumées dans la section Conclusions.

Méthodes

L'utilisation de matériaux poreux dans les supercondensateurs et le mode spécifique d'accumulation de charge font que les approches traditionnelles basées sur des modèles dérivés d'ordre entier ne sont pas assez précises. De nombreux chercheurs ont proposé diverses solutions sous forme de combinaison de RC typiques éléments à valeurs constantes ou variables [4, 7]. Mais il s'avère qu'une précision nettement meilleure peut être obtenue en utilisant un calcul différentiel d'ordre non entier pour définir les relations entre le courant et la tension du supercondensateur [17, 19]. De plus, une telle solution peut aboutir à une structure de modèle très simple, tout en offrant une très grande précision [18].

Différo d'ordre fractionnaire–Calcul intégral

Le calcul différentiel d'ordre fractionnaire est connu depuis plus de 300 ans. Cependant, seules quelques années récentes ont apporté sa popularité dans la modélisation des phénomènes et des processus physiques. On pense que la description de la dynamique avec une dérivée ou une intégrale d'ordre non entier peut être l'une des méthodes les plus efficaces pour la modélisation des propriétés réelles de nombreux phénomènes complexes et processus industriels, en particulier sur la base de nouveaux matériaux et technologies [10, 12, 13 , 32–34].

Le calcul différentiel ou intégral d'ordre non entier est une généralisation du calcul classique à l'ordre α qui appartient à l'ensemble des nombres réels \(\mathcal {R}\). L'opérateur différo-intégral d'ordre \(\alpha \in \mathcal {R}\) de la fonction f (t ) sur la plage [a ,t ] peut s'écrire comme suit

en supposant que la fonction f (t ) est plusieurs fois dérivable et intégrable. Quant à l'opérateur (1), il existe de nombreuses définitions de sa réalisation. Ces définitions diffèrent par leurs propriétés et leurs domaines d'application. Les plus populaires sont les définitions de Riemann-Liouville, Caputo et Grünwald-Letnikov (GL) [34]. Ce dernier sera utilisé dans cet article sous la forme

où le binôme \(\alpha \choose j\) est défini comme suit

Afin d'obtenir un modèle fractionnaire à des instants discrets, la définition GL sous une forme discrète est simplifiée comme

Il existe plusieurs schémas de discrétisation pour le GL Eq. (4). Les plus populaires incluent les différences vers l'arrière (Euler), les opérateurs trapézoïdaux (Tustin) et Al Alaoui. En utilisant la méthode d'Euler, la dérivée fractionnaire aux instants discrets k peut être présenté comme

La somme infinie des échantillons précédents doit être dans les systèmes réels limitée à une valeur finie en raison de la mémoire limitée et du temps de calcul limité. Maintenant, l'approximation en temps discret tronqué ou de longueur finie de GL est

où f (l )=0 pour l <0 et L est la longueur du modèle (6) [23]. La réduction du nombre d'échantillons entraîne une diminution de la précision des calculs. Ceci est important pour les systèmes fonctionnant dans un temps continu. D'autres types de solutions sont des algorithmes approchant des différentielles-intégrales fractionnaires avec des modèles d'ordre entier. Un exemple peut être les filtres récursifs d'Oustaloup [35]. Un autre modèle efficace de longueur finie est le FFLD, qui est une combinaison du modèle tronqué (6) et d'une différence basée sur Laguarre [24, 36, 37].

Tous les résultats d'identification ainsi que les mesures d'énergie sont obtenus sur la base de tous les échantillons dans la (longue) fenêtre d'observation L , c'est-à-dire avec une précision maximale. La figure 1 présente les réponses échelonnées d'intégration et de différenciation obtenues sur la base de (6), pour k =0,1,…,L et pour diverses valeurs d'ordre d'intégration/différenciation α . En supposant différentes valeurs d'ordre α , on peut modéliser plus précisément différents processus physiques, en particulier ceux de diffusion.

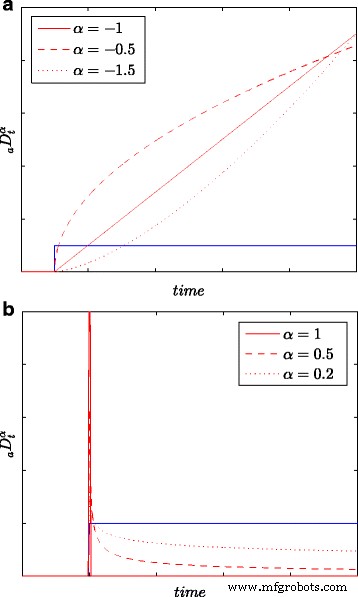
Réponses par étapes pour l'intégration (a ) et différenciant (b ) modèles avec diverses commandes α

Estimation des paramètres pour le modèle fractionnaire

Les résultats de toutes les mesures d'énergie et procédures d'identification présentées dans cet article ont été obtenus pour un supercondensateur chargé à partir d'une source de tension contrôlée. Dans un tel système, le courant du supercondensateur i _C (t ) doit être limité par une résistance R connecté en série avec le supercondensateur C (Fig. 2). L'estimation de tous les paramètres du supercondensateur est effectuée sur la base de la réponse quadripôle u _C (t ) au pas de tension u (t ) à son entrée. Choisir la valeur appropriée de l'ordre dérivé α permet de rendre compte d'un modèle supercondensateur des phénomènes physiques liés aux processus de diffusion associés à la redistribution des charges au cours des processus de charge et de décharge. La résistance parallèle r _P permet en outre de modéliser le courant de fuite. En utilisant le calcul différentiel fractionnaire pour la modélisation des supercondensateurs, la structure du modèle peut être de faible complexité. Pour un supercondensateur chargé à partir de la source de tension, un modèle se compose de seulement deux éléments, c'est-à-dire un simple RC quadripôle (Fig. 2a). Pour les faibles capacités, la résistance série r _S est important (Fig. 2b), tandis que le courant de fuite I _L peut être en outre représenté par la résistance parallèle r _P (Fig. 2c). En utilisant le calcul de l'ordre fractionnaire pour modéliser le supercondensateur, la relation entre la tension aux bornes du condensateur et son courant peut être exprimée comme suit

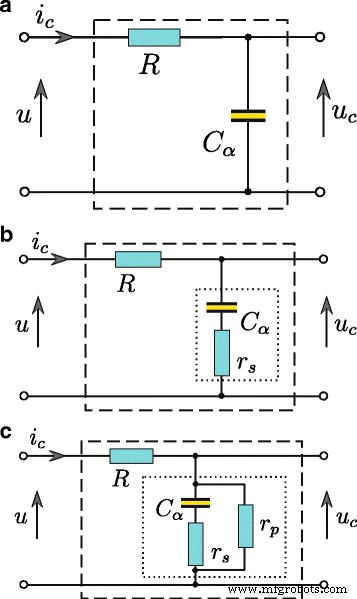
Supercondensateur RC modèles, modèle de base (a ), élargi avec une résistance série (b ), et avec une résistance parallèle supplémentaire (c )

où l'opérateur d ^α /dt ^α désigne un opérateur de différenciation d'ordre α et l'unité SI de C _α est [F/sec ^1−α ]. La configuration de base du supercondensateur présentée sur la figure 2a peut être traitée comme un système inertiel de premier ordre et peut être représentée par la fonction de transfert fractionnaire

où T =R C _α . Prise en compte de la résistance série r _S (Fig. 2b), le circuit est traité comme un système de correction à retard de phase avec la fonction de transfert (comparer [24])

où T ₁ =C _α (R +r _S ) et T ₂ =r _S C _α . De plus, en tenant compte de la résistance parallèle r _P représentant le courant de fuite I _L (Fig. 2c), la fonction de transfert du système peut être exprimée par

où K =R /r _P +1, T ₁ =C (R r _s /r _P +R +r _S ) et T ₂ =r _S C . Dans le domaine temporel, l'Eq. (10) peut être présenté comme

La réponse temporelle du modèle défini par (11) a été obtenue en le transformant sous la forme présentée graphiquement sur la figure 3, où les opérations d'intégration et de différenciation sont d'ordre fractionnaire α . Ce modèle a été utilisé lors du processus d'estimation des paramètres des supercondensateurs. Le supercondensateur testé a été identifié à l'aide du système présenté sur la figure 4a. La procédure de contrôle de l'ensemble du système a été développée à l'aide du logiciel Matlab/Simulink avec xPC Toolbox. Le système se composait d'un PC de bureau (xPC Target) avec la carte de mesure NI-DAQ installée et un ordinateur maître (xPC Host). Les ordinateurs étaient interconnectés via le réseau Ethernet. Le supercondensateur a été chargé et déchargé par une source de tension (contrôlée en tension) (Fig. 4b) d'une efficacité de courant jusqu'à ± 3 A. Le système de mesure a fonctionné avec la fréquence d'échantillonnage de 100 Hz, tandis que toutes les mesures et les signaux de commande analogiques étaient traité avec une résolution de 16 bits [25].

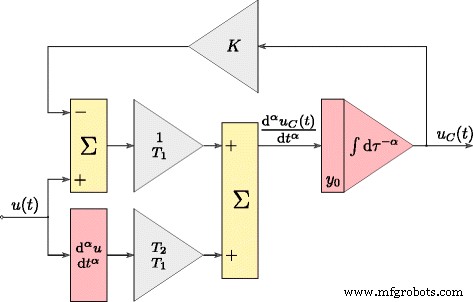
Structure Matlab du modèle de supercondensateur dans le domaine temporel

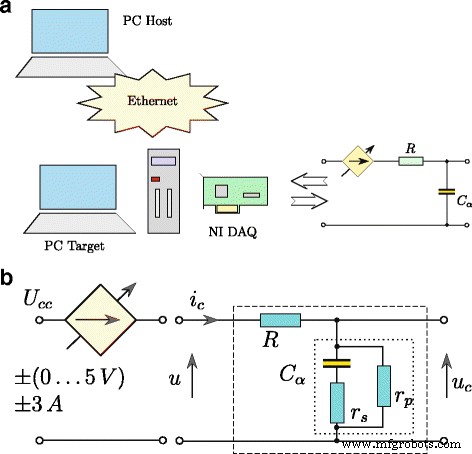
Structure du système de mesure (a ) et schéma de charge/décharge des supercondensateurs (b )

La principale méthode pour déterminer les propriétés dynamiques d'un système est basée sur l'analyse de la réponse indicielle [38]. Par rapport au modèle du système, cette méthode permet d'estimer ses paramètres. Pour cette étude, le signal de pas avec différentes tensions (0,5/1,0/1,5/2,0/2,7 V) et une durée constante (500 s) ont été utilisés (voir Fig. 5 et Tableau 2). D'autre part, l'une des applications typiques des supercondensateurs est l'accumulation ou la fourniture d'énergie dans les systèmes électriques. Dans ce cas, le taux de changement de tension est plutôt faible. Pour le simuler, le signal 400 mVpp et 0,03 rad/s avec un décalage de 2 V a été utilisé (Fig. 6). De plus, afin d'examiner l'influence des changements de tension et de fréquence sur les paramètres estimés, diverses valeurs de ces derniers ont été utilisées (voir tableau 3).

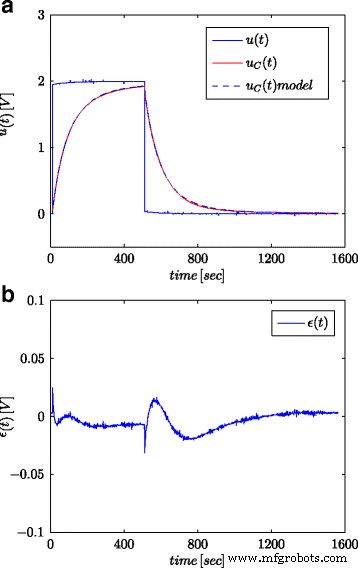
Réponses indicielles pour le supercondensateur testé et son modèle fractionnaire (a ) et l'erreur de réponse du modèle (b )

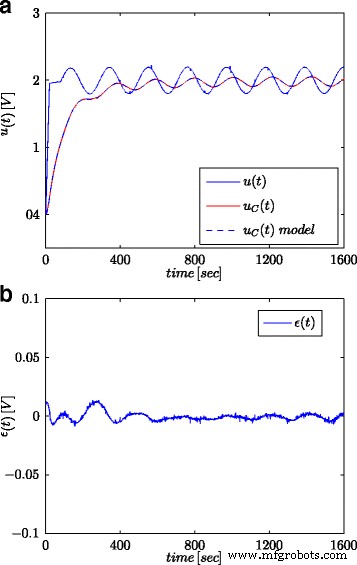
Réponses d'onde sinusoïdale pour le supercondensateur testé et son modèle fractionnaire (a ) et l'erreur de réponse du modèle (b )

Il existe plusieurs méthodes pour estimer les paramètres du modèle. L'objectif principal de la procédure d'identification dans le domaine temporel appliquée dans ce travail était d'estimer le vecteur de paramètres inconnus θ =[α ,C _α ,r _S ,r _P ] du modèle fractionnaire présenté par (11). La méthode des moindres carrés a été utilisée pour minimiser l'erreur initiale. Un critère d'optimisation impliquait la minimisation de l'erreur standard \(\|\epsilon (k)\|_{2}^{2}\), où

où u _C (k ) est la tension de sortie mesurée à partir du système testé à l'instant k , tandis que \(\hat {u}_{C}(k)\) est la tension de sortie du modèle considéré pour le signal d'entrée u (k ). Le problème d'identification se réduit maintenant à trouver un vecteur de paramètres θ ∈Θ _annonce qui minimiserait le critère carré J de telle manière que

où Θ _annonce désigne l'ensemble des valeurs de paramètres admissibles et N signifie le temps de simulation. Il existe de nombreux algorithmes d'optimisation qui peuvent être utilisés pour résoudre le problème (13). Les résultats présentés dans cet article ont été obtenus en implémentant l'algorithme génétique dans l'environnement Matlab.

Calcul d'énergie

Une variation de l'énergie stockée dans le supercondensateur dépend de la puissance fournie au condensateur par unité de temps et peut être décrite comme suit

En exprimant la puissance fournie au condensateur comme un produit du courant et de la tension aux bornes du condensateur, la variation d'énergie à un instant donné t peut être exprimé par

L'énergie totale pendant l'intervalle de temps [t ₁ ,t ₂ ] peut être obtenu en intégrant les changements d'énergie au cours de cette période

Comptabilisation de l'éq. (7), le stockage d'énergie total peut être déterminé comme

En supposant t ₁ =0 et \(E_{t_{1}}=0\), l'énergie totale stockée dans le supercondensateur pendant l'intervalle de temps [0,t ] est

Notez que pour α =1 Éq. (18) peut être réduit au classique

Résultats et discussion

Initialement, la procédure d'estimation du vecteur de paramètre du modèle de supercondensateur à l'aide du calcul fractionnaire a été effectuée. L'estimation a été effectuée sur la base du système présenté sur la figure 2c, générant un échelon de tension ou une onde sinusoïdale à son entrée. Les réponses du modèle ont été calculées sur la base de (11). Les résultats obtenus par les deux procédures d'identification sont très similaires, notamment dans le cas de la capacité fractionnaire C _α et l'ordre fractionnaire α (voir tableau 1). Quelques différences dans les estimations de résistance en série r _S peut être le résultat de sa dépendance à la fréquence. Le signal de pas se compose de nombreuses harmoniques à haute fréquence tandis que l'onde sinusoïdale n'en a qu'une seule – le 0,03 rad/s. Les résultats présentés ont été obtenus pour le supercondensateur commercial Samwha Green-Cap EDLC (DB), évalué à 2,7 V avec une capacité nominale de 100 F et 8 mΩ résistance série équivalente maximale (r _S ) à 1 kHz.

Les figures 5a et 6a montrent la tension de supercondensateur mesurée et les réponses de modèle calculées, pour les signaux échelonnés et sinusoïdaux, respectivement, tandis que les figures. 5b et 6b montrent l'erreur de réponse du modèle.

Tous les résultats obtenus montrent une cohérence élevée entre les réponses du modèle et les mesures réelles malgré le fait que des modèles relativement simples ont été proposés. Certaines divergences peuvent résulter du fait que les paramètres du modèle doivent être estimés dans le système de supercondensateurs chargés et déchargés à l'aide de la source de courant [25]. En outre, des estimations très élevées de r _P peut suggérer que cette résistance pourrait être exclue du modèle de supercondensateur illustré à la figure 2c. Ces estimations très élevées et leurs fortes divergences pour les différentes entrées indiquent que les signaux de test utilisés pour estimer ce paramètre ne sont pas appropriés. Le modèle (10) a été utilisé comme forme la plus générale. Cependant, afin de déterminer avec précision tous ses paramètres, il était nécessaire d'utiliser d'autres procédures et signaux de test. La valeur de r _P caractérise le courant de fuite I _L et doit être déterminé à l'aide du signal à tension constante, mais pour une durée très longue – de l'ordre de plusieurs dizaines d'heures.

Bien que l'objectif principal de l'étude était de mesurer l'énergie, diverses conditions d'excitation ont largement affecté toutes les estimations de paramètres (voir le tableau 2). Par exemple, l'augmentation de l'amplitude du pas de tension a modifié de manière significative l'ordre d'intégration fractionnaire, en raison de l'effet croissant des phénomènes de diffusion à l'intérieur du supercondensateur. On peut également voir dans le tableau 2 que le supercondensateur est assez non linéaire. En raison des changements d'ordre d'intégration, la variation de la capacité fractionnelle est également observée. Ceci s'applique également à l'excitation sinusoïdale. Les valeurs des paramètres estimés, en particulier α et C _α — dépendent de l'amplitude et de la fréquence (voir tableau 3). Pour les basses fréquences, la valeur d'amplitude est importante, tandis que pour les fréquences plus élevées, le supercondensateur se comporte comme s'il était excité avec une tension constante.

Calcul d'énergie

Les figures 7a et 8a montrent les valeurs mesurées de la tension et du courant du supercondensateur pour la configuration présentée sur la figure 4b. Ces valeurs ont été utilisées pour le calcul de l'énergie totale stockée dans le condensateur (marqué comme E ₁ dans les Fig. 7b et 8b) selon (16). Tout comme pour les processus d'identification des paramètres, les calculs ont été effectués à la fois pour le pas de tension et l'onde sinusoïdale à l'entrée du système. L'énergie ainsi calculée pour chaque instant t a été comparée à l'énergie calculée sur la base de la tension et de la capacité conformément à (19) (marquée comme E ₃ dans les Fig. 7b et 8b) et l'énergie calculée avec le calcul d'ordre fractionnaire (marqué comme E ₂ dans les Fig. 7b et 8b) selon (18). Pour l'éq. (19), une valeur nominale de supercondensateur a été adoptée (C _n ), tandis qu'en (18) la valeur obtenue à partir du processus d'estimation présentée dans le tableau 1 a été utilisée. La figure 7b montre les résultats des mesures et des calculs d'énergie pour le pas de tension, tandis que la figure 8b montre ces mêmes quantités pour l'onde sinusoïdale. Des calculs similaires ont été effectués pour différents échelons de tension et excitations sinusoïdales. La figure 9a, b montre un exemple d'énergies mesurées et calculées pour deux échelons de tension de 0,5 V et 2,7 V, respectivement. La figure 10 montre les changements d'énergie pour un signal sinusoïdal avec la fréquence de 0,03 rad/sec et différentes amplitudes de 0,1/0,25/0,5 et 0,7 V. On peut voir que les différences dans les valeurs d'énergie déterminées correspondent à des différences dans les valeurs estimées de l'ordre fractionnaire α . Plus la différence par rapport à la valeur − 1 est grande, plus la différence entre les énergies calculées est grande.

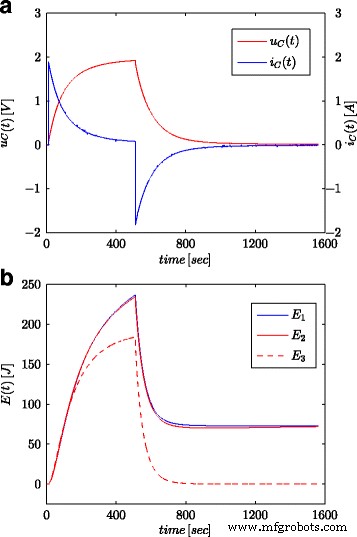
Réponses indicielles pour la tension et le courant du supercondensateur (a ) et les valeurs énergétiques calculées (b )

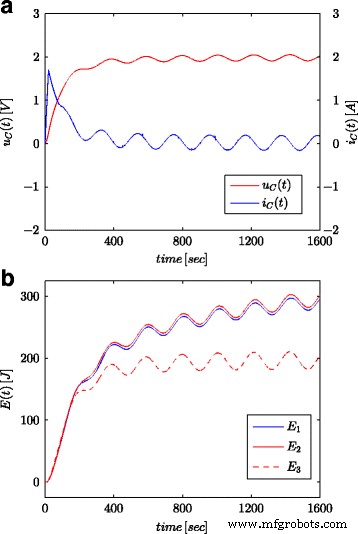
Réponses sinusoïdales pour la tension et le courant du supercondensateur (a ) et les valeurs énergétiques calculées (b )

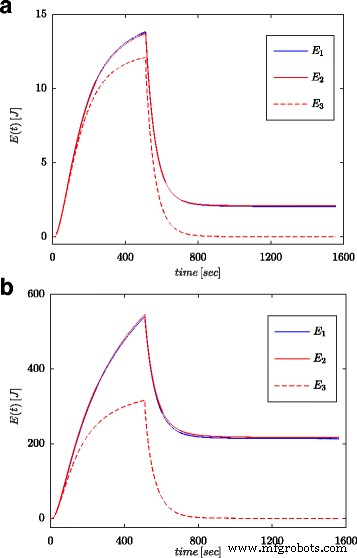
Quantités d'énergie calculées pour des excitations de pas de 0,5 V (a ) et 2,7 V (b )

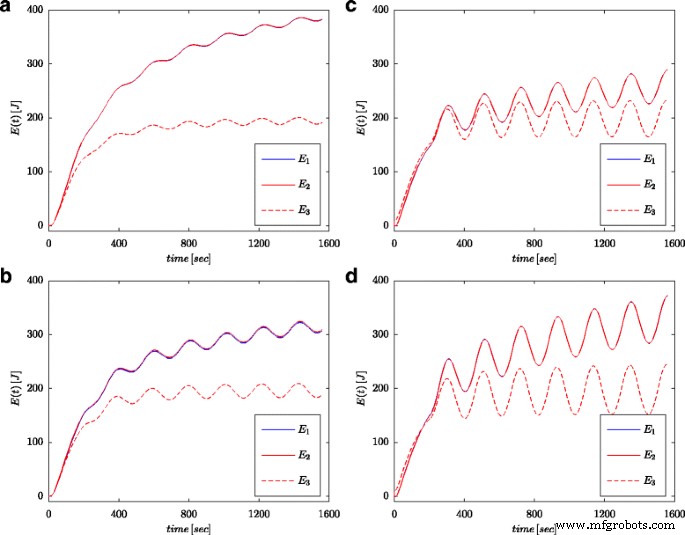
Quantités d'énergie calculées pour des excitations sinusoïdales avec une fréquence de 0,03 rad/s et des amplitudes de 0,1 V (a ), 0,25 V (b ), 0,5 V (c ), et 0,7 V (d )

Discussion

L'utilisation d'électrodes en matériau poreux dans les supercondensateurs sous forme de charbon actif isolé par un séparateur très mince et l'utilisation de mécanismes d'accumulation de charges comme ce qu'on appelle une double couche, donne une énorme augmentation de leur capacité. Cependant, l'application de nouveaux matériaux et de nouvelles solutions de conception fait que les calculs mathématiques traditionnels sous forme de dérivées et d'intégrales d'ordre entier semblent inexacts. Les mesures et calculs effectués prouvent la nature d'ordre fractionnaire des supercondensateurs. Par estimation correcte de l'ordre non entier α de dérivée/intégrale, on peut modéliser avec précision les phénomènes et les processus se produisant à l'intérieur du supercondensateur à l'aide de modèles mathématiques simples.

En tenant compte de la valeur réelle de l'énergie accumulée déterminée par (16), le modèle d'ordre entier avec des paramètres nominaux (19) sous-estime la quantité d'énergie, tandis que le modèle fractionnaire (18) indique presque la même valeur.

Les tests et mesures effectués portaient sur la charge et la décharge du supercondensateur par une source de tension. Dans des conditions industrielles, les supercondensateurs sont généralement chargés et déchargés par des sources de courant. Cela peut changer la nature du système car le condensateur n'est plus un système inertiel mais devient un système intégrateur typique. Cependant, les mesures effectuées par l'auteur indiquent également l'apparition de processus de diffusion dans de tels cas. Quoi qu'il en soit, l'utilité de la dérivée/intégrale de Gründwald-Letnikov est confirmée ici. Un autre problème est lié à la mise en œuvre de l'opérateur différentiel-intégral GL comme, par exemple, la différence GL finie ou tronquée (6), qui peut être lourde en termes de calcul. Dans des recherches futures, nous comparerons les approximations Oustaloup [35] et FFLD [24, 36, 37] pour résoudre efficacement le problème d'implémentation.

La quantité d'énergie stockée dans le supercondensateur calculée uniquement sur la valeur mesurée de la tension aux bornes du supercondensateur et en utilisant le modèle (19) n'est pas appropriée. Le modèle (19) n'est valable que si le courant du condensateur est caractérisé par la dérivée d'ordre entier de la tension du condensateur (i _C (t )=du _C (t )/dt ). Ce n'est pas vrai pour le supercondensateur en raison de sa construction et de l'utilisation de matériaux spéciaux. Cependant, le même problème se produit avec de très gros supercondensateurs chargés par une source de courant. Il y a aussi des éléments assez nouveaux comme les super-batteries. Dans toutes ces applications, les changements de courant ne sont pas caractérisés par la dérivée d'ordre entier de la tension aux bornes en raison des propriétés spécifiques de ces éléments.

Conclusions

Dans cet article, une nouvelle approche pour l'estimation d'une quantité d'énergie accumulée dans les supercondensateurs a été présentée. L'analyse a été menée en tirant parti de certaines propriétés uniques des modèles d'ordre fractionnaire. Il a été démontré que l'application d'une modélisation aussi sophistiquée conduit à des résultats très précis, qui peuvent être obtenus même si les modèles eux-mêmes ne sont pas d'une grande complexité. Cela est dû à une capacité naturelle de la dynamique d'ordre non entier à modéliser les processus de diffusion, tout comme la redistribution de charge dans les supercondensateurs. Les résultats de cet article ont confirmé la nature fractionnaire des supercondensateurs.