Une expression développée du potentiel chimique pour une déformation rapide dans les électrodes à nanoparticules des batteries lithium-ion

Introduction

Pour le développement d'appareils électroniques portables, de véhicules électriques et de stockage d'énergie à grande échelle, il est proposé d'appliquer un certain nombre de matériaux d'électrode à haute capacité tels que le silicium, qui subissent des changements de volume extrêmes pendant la lithiation, dans les batteries au lithium [1,2 ,3]. La contrainte induite par la déformation volumétrique homogène est appelée contrainte induite par diffusion, qui peut induire une rupture fragile pendant la charge et la décharge cycliques, et cet effet négatif dégrade davantage la capacité de la batterie [4]. Les matériaux composites des électrodes des batteries lithium-ion sont généralement complexes et leurs morphologies sont différentes, ce qui rend plus difficile l'explication du comportement des batteries par la théorie ou l'équation. Dans les modèles théoriques, les propriétés des matériaux composites sont généralement simulées en considérant les changements des paramètres du matériau des électrodes dans les coordonnées spatiales, tandis que l'effet d'interface des matériaux composites est ignoré. À l'heure actuelle, trois formes d'électrodes typiques, c'est-à-dire sphérique, cylindrique et plaque, sont principalement considérées dans le modèle théorique. Parmi eux, les formes sphériques et cylindriques sont généralement des modèles unidimensionnels, et des modèles unidimensionnels et bidimensionnels pour les électrodes à plaques sont disponibles. Récemment, un certain nombre d'études se sont concentrées sur le stress induit par la diffusion dans les électrodes à nanoparticules de silicium des batteries lithium-ion. Par exemple, Yang et al. [5] ont présenté un modèle chimio-mécanique pour étudier la transformation de phase induite par la lithiation, l'évolution morphologique, la génération de contraintes et la fracture dans les nanofils de silicium cristallin. Li et al. [6] ont étudié l'effet de la vitesse locale sur le stress induit par la diffusion dans des électrodes à nanoparticules de silicium. Zhao et al. [7] ont analysé la contrainte induite par la diffusion en tenant compte de la déformation inélastique du matériau hôte. Dans tous ces travaux susmentionnés, la physique fondamentale impliquée est la diffusion atomique ou ionique dans les solides sous de multiples forces motrices. La diffusion atomique dans un solide peut changer la composition solide de son état stoechiométrique et être affectée par la contrainte induite par la diffusion. Une telle interaction de contrainte et de diffusion est régie par l'équilibre thermodynamique des solides.

Larche et Cahn [8] ont développé un cadre thermodynamique pour les solides à plusieurs composants qui atteignent l'équilibre sous une contrainte non hydrostatique. Le cadre était basé sur l'hypothèse que la déformation causée par le changement de composition est faible et isotrope. En conséquence, un potentiel chimique dépendant du stress a été introduit pour tenir compte de l'interaction entre le stress et la diffusion. Wu [9] a dérivé un potentiel chimique dépendant de la contrainte différent dans lequel le tenseur de quantité de mouvement d'Eshelby est impliqué au lieu de la contrainte hydrostatique de Cauchy. Sur cette base, Cui et al.[10] ont proposé un nouveau potentiel chimique pour la déformation finie des solides. Cependant, dans ces travaux, la dérivation n'est rigoureuse que lorsque la déformation est faible ou que la vitesse de déformation est suffisamment faible par rapport à la diffusion. Il est susceptible de faire une erreur significative pour une électrode de silicium en raison de sa grande expansion volumétrique de composition (∼  400 %) lorsqu'elle est lithiée rapidement.

Dans cet article, nous présentons une expression développée du potentiel chimique sans l'hypothèse d'un faible taux de déformation, distincte de l'expression traditionnelle de Cui [10]. Ce modèle est établi pour la déformation rapide des électrodes pendant la charge ou la décharge et est indépendant des morphologies car le potentiel chimique est une quantité intensive plutôt qu'extensive. La différence entre ces deux expressions de potentiel chimique sur les distributions de contrainte et de concentration en Li est analysée sous des opérations potentiostatiques et galvanostatiques dans des électrodes à nanoparticules de Si. Le résultat révèle que la différence augmente avec l'augmentation du taux de déformation. Un rayon critique, où il n'y a pas de différence entre le flux de Li causé par ces deux expressions de potentiel chimique ainsi que la contrainte hydrostatique de Cauchy pendant la majeure partie du processus lithié, est trouvé en même temps.

Méthodes

Équations mécaniques

L'insertion de lithium dans les électrodes peut provoquer un changement volumétrique. Pour plus de commodité, nous utilisons deux manières de décrire la déformation et le mouvement des solides, à savoir la description lagrangienne et la description eulérienne. Le mouvement des particules matérielles dans un milieu continu peut être décrit par

où x est les coordonnées d'Euler, X est les coordonnées de Lagrange, et U est le champ de déplacement. Le changement de forme du solide continu peut être caractérisé par le tenseur de gradient de déformation, donné par

où Grad représente l'opérateur de gradient dans la description lagrangienne, et I est le tenseur unitaire du second ordre.

Pour une particule sphérique, les coordonnées de Lagrange et les coordonnées d'Euler d'un point matériel sont respectivement (R, Θ, Φ) et (r, θ, φ) dans le système sphérique. Ensuite, le tenseur gradient de déformation F se trouve comme

Lors de la charge ou de la décharge, le changement de forme de l'électrode peut être divisé en deux processus :(a) un changement de forme dû à l'insert de lithium et (b) une déformation élastique réversible. Ces deux processus de déformation peuvent être décrits par deux tenseurs de gradient séparés et le tenseur de gradient de déformation totale peut être écrit comme

où F ^e représente la déformation élastique, F ^c représente le changement de forme dû à l'insert de lithium. L'équation (4) représente le processus du matériau d'électrode de l'état initial (non déformé) à l'état actuel (déformé). En supposant que le changement de forme dû à l'insert de lithium est isotrope, F ^c peut être donné par

où représente le volume molaire partiel.

De l'éq. (3–5), le tenseur gradient de déformation élastique F ^e est

Le tenseur total des déformations de Green-Lagrange E peut être écrit comme

où le tenseur de déformation élastique E ^e et tenseur de déformation induit par diffusion E ^c sont

respectivement.

En substituant l'équation. (6) dans l'Éq. (8), les composantes radiale et tangentielle du tenseur de déformation de Green-Lagrange sont

La relation constitutive de la déformation peut être déterminée à partir de la densité d'énergie de déformation comme

où W est la densité d'énergie de déformation élastique dans la description lagrangienne, et P est le premier stress de Piola-Kirchhoff. De plus, si le matériau est linéairement élastique, W peut être écrit comme une fonction quadratique du tenseur de déformation de Green-Lagrange

Ici, E _h et ν sont respectivement le module de Young et le coefficient de Poisson, C est le tenseur de rigidité, et det(F ^c ) est le déterminant du tenseur du gradient de déformation pour la déformation induite par la diffusion.

Enfin, la première contrainte de Piola-Kirchhoff est donnée par

Combinant les équations. (5), (9), (10) et (13), les composants correspondants du premier tenseur de contraintes de Piola-Kirchhoff (P-K) sont

Et la première contrainte P-K doit satisfaire la condition d'équilibre en l'absence de force corporelle

avec conditions initiales et aux limites

Équation de transport de masse

La concentration et le flux de diffusion du lithium dans les électrodes, qui sont fonctions des coordonnées et du temps, seront appelés C (X , t) et J (X , t) dans la description lagrangienne, et ils devraient être satisfaits de l'équation de transport de masse écrite sous la forme

où Div représente l'opérateur de divergence dans la description lagrangienne. Compte tenu de la caractéristique de symétrie sphérique, la diffusion ne se produit que dans la direction radiale et nous utilisons J (R , t) pour représenter la composante radiale de J (X , t). Dans le système sphérique, l'Eq. (18) devient

La diffusion du lithium dans les électrodes est entraînée par le gradient de potentiel chimique et le flux radial J (R , t) est proportionnel au gradient de potentiel chimique μ , comme [11]

où D est la diffusivité, R _g est la constante des gaz, et T est la température. μ est défini comme l'écart de la densité d'énergie totale par rapport à la concentration et peut être écrit comme

Supposons que la densité d'énergie du système, , puisse être décrite comme la somme de la densité d'énergie chimique et de la densité d'énergie de déformation. Ainsi, la densité d'énergie interne totale peut être écrite comme

En substituant l'équation. (22) dans l'équation (21), le potentiel chimique μ peut être démontré être

où μ ₀ (C ) et τ (E ^e , C ) sont respectivement les parties indépendantes de la contrainte et dépendantes de la contrainte du potentiel chimique. Et

où μ ₀ est une constante qui représente le potentiel chimique à un état standard, et γ est le coefficient d'activité qui représente les effets des interactions entre les atomes/molécules. Pour une solution diluée, les interactions entre les atomes/molécules sont négligeables; ainsi, γ = 1.

Nous nous concentrons sur la partie dépendant du stress du potentiel chimique τ (E ^e , C), qui est la dérivée de la densité d'énergie de déformation W par rapport à la concentration de lithium C. Traditionnellement, (X , t) est considérée comme la densité d'énergie libre de Helmholtz et donc cette étape est effectuée pour une déformation fixe notée [11]

L'indice H signifie qu'il est causé par la densité d'énergie libre de Helmholtz. Le potentiel chimique s'avère être

où σ _m est la contrainte hydrostatique de Cauchy dans la description eulérienne et peut être obtenue par

Il est à noter que la rigidité C du matériau de l'électrode est supposée indépendante de la concentration de lithium C dans l'éq. (12). De plus, det(F ^e ) ≈ 1 est largement accepté de sorte qu'il est généralement ignoré. Dans la suite de cet article, nous appelons l'équation. (26) comme expression traditionnelle du potentiel chimique. Par contre, (X , t) est considérée comme la densité d'énergie libre de Gibbs dans certaines études [12, 13] sur le modèle de champ de phase de sorte que nous ne pouvons pas obtenir une expression développée de τ (E ^e , C), et

L'indice G signifie qu'il est causé par la densité d'énergie libre de Gibbs. Dans ce cas, μ devient

et nous appelons l'équation. (29) comme expression développée du potentiel chimique.

L'équation de transport de masse est constituée par les équations. (19), (20), (26) et (29) avec des expressions traditionnelles et développées du potentiel chimique. Dans la partie restante de cet article, nous comparerons les effets de ces deux expressions du potentiel chimique sur le stress induit par la diffusion et la concentration de Li sous différentes méthodes de charge.

En thermodynamique, l'énergie libre de Helmholtz est un potentiel thermodynamique qui mesure le travail utile pouvant être obtenu à partir d'un système thermodynamique fermé à température et volume constants. En revanche, l'énergie libre de Gibbs mesure le maximum de travail réversible qui peut être effectué par un système thermodynamique à température et pression constantes. Dans les solides à faible niveau de contrainte, l'énergie libre de Gibbs est approximativement équivalente à l'énergie libre de Helmholtz, car la déformation des solides est généralement faible. Cette hypothèse convient à la plupart des matériaux solides en raison de leur faible déformation induite par diffusion, mais à l'exception du silicium en raison de sa grande expansion volumétrique lors de la lithiation. En fait, la diffusion et la déformation ont lieu en même temps, de sorte qu'il ne convient pas de supposer qu'il n'y a pas de déformation pendant que la concentration change. Même ainsi, comme on peut le voir à partir de l'Eq. (25), l'expression traditionnelle du potentiel chimique est toujours exacte lorsque le taux de déformation est suffisamment faible. Cependant, il est susceptible de provoquer de grandes erreurs lorsqu'une électrode à nanoparticules de Si est lithiée rapidement.

L'électrode est lithiée avec une concentration constante de lithium-ion à sa surface, à savoir le fonctionnement potentiostatique, ou avec un flux constant à sa surface, à savoir le fonctionnement galvanostatique. Les conditions aux limites de l'équation. (19) sont

respectivement. La condition initiale s'écrit

pour chaque opération de charge. Ici, C _max est la concentration maximale en lithium du matériau et j ₀ est une constante représentant le courant de charge.

Implémentation numérique

Il est très difficile d'obtenir la solution analytique du système ci-dessus constitué d'équations aux dérivées partielles, voire impossible. Avec les équations. (1)–(3) et (13)–(18), nous calculons numériquement l'évolution du stress induit par la diffusion et de la concentration en lithium en utilisant le logiciel multiphysique COMSOL. La lithiation d'une nano-électrode de silicium sous des opérations potentiostatiques et galvanostatiques est étudiée, avec différentes expressions de potentiel chimique. Les propriétés matérielles du Si et les paramètres de fonctionnement utilisés dans la simulation sont répertoriés dans le tableau 1. Pour plus de commodité, la substitution sans dimension correspondante de la coordonnée, de la contrainte et de la concentration est utilisée dans les figures.

Pour étudier la différence entre les différentes expressions du potentiel chimique à différents moments dans l'électrode Si sphérique, l'état de charge (SOC) est calculé comme

Les flux de diffusion induits par les contraintes dans la description lagrangienne sont décrits comme

représentant respectivement le flux causé par différentes expressions de potentiel chimique.

Résultats et discussion

La figure 1 montre la distribution spatiale de la concentration de lithium, de contrainte radiale et de contrainte circonférentielle dans une électrode Si sphérique en fonctionnement galvanostatique à plusieurs SOC. À titre de comparaison, les résultats numériques avec les expressions développées et traditionnelles du potentiel chimique sont inclus et ils sont représentés par des lignes pleines et des symboles triangulaires, respectivement. Pour chaque SOC de la figure 1a, la ligne continue chevauche presque les symboles triangulaires. L'effet causé par les différentes expressions du potentiel chimique sur la concentration de lithium peut être ignoré. Sur la figure 1b et la figure 1c, pour les SOC de 46,7% et 65,5%, les lignes continues sont plus hautes que les triangles au centre, alors qu'elles se chevauchent presque à l'extérieur, tout comme dans les autres SOC. Globalement, il y a un léger effet sur la concentration en lithium et les contraintes en fonctionnement galvanostatique. La figure 2 montre les distributions spatiales de la concentration de lithium, de contrainte radiale et de contrainte circonférentielle dans une électrode Si sphérique sous fonctionnement potentiostatique à plusieurs SOC. Il convient de mentionner que les contraintes radiales et circonférentielles augmentent d'abord puis diminuent avec l'augmentation du SOC sur les figures 1 et 2. C'est parce que l'électrode de silicium à l'état initial ou à l'état entièrement lithié est sans contrainte, car il n'y a pas de gradient de concentration. Par rapport à la figure 1a, la différence entre les lignes pleines et les triangles est plus importante sur la figure 2a. En raison de la concentration de lithium sur la surface est un C constant _max en fonctionnement potentiostatique, le taux de charge est supérieur au taux de déformation, celui du fonctionnement galvanostatique et le taux de déformation également. Cependant, la déformation totale sous le même SOC est presque la même quelle que soit la méthode de charge, prenant juste un temps différent. Il indique que l'influence sur la distribution du lithium causée par différentes expressions du potentiel chimique n'est liée qu'à la vitesse de déformation plutôt qu'à la déformation et augmente avec l'augmentation de la vitesse de déformation. En effet, les expériences existantes montrent que les électrodes de silicium se déforment très rapidement lors de la lithiation sous certains modes de charge. Comme on peut le voir sur la figure 3 [17], l'anode en Si est complètement déformée en 1 min avec un potentiel de 2 V par rapport au métal Li. Dans cette condition, les résultats résolus par ces deux expressions de potentiel chimique seront significativement différents. Malheureusement, dans ce cas, la contrainte de l'électrode ne peut pas être mesurée avec précision et ne peut donc pas être comparée quantitativement à notre modèle.

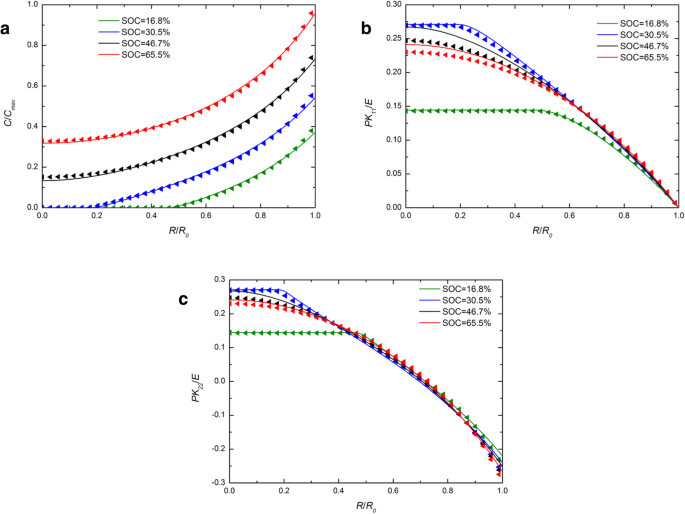
Distribution spatiale de (a ) la concentration de lithium, (b ) contrainte radiale, et (c ) contrainte circonférentielle dans une électrode Si sphérique à différents SOC sous fonctionnement galvanostatique (les lignes pleines représentent les résultats avec l'expression traditionnelle du potentiel chimique ; les lignes triangulaires représentent les résultats avec l'expression développée du potentiel chimique)

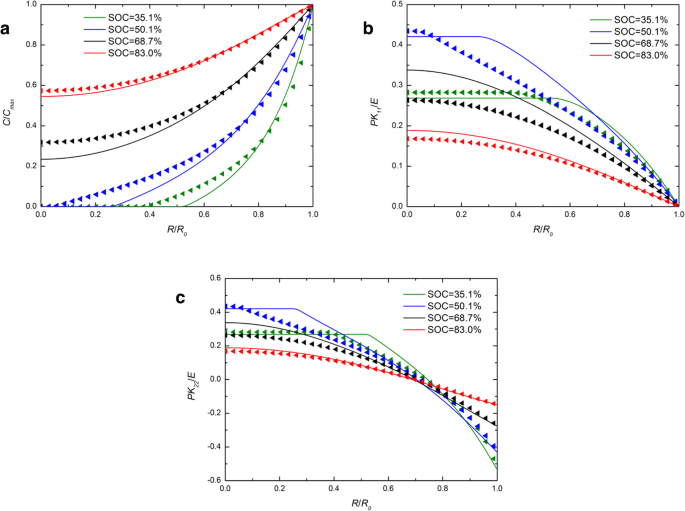
Distribution spatiale de (a ) la concentration de lithium, (b ) contrainte radiale, et (c ) contrainte circonférentielle dans une électrode sphérique à nanoparticules de Si à différents SOC sous fonctionnement potentiostatique (les lignes pleines représentent les résultats avec l'expression traditionnelle du potentiel chimique ; les lignes triangulaires représentent les résultats avec l'expression développée du potentiel chimique)

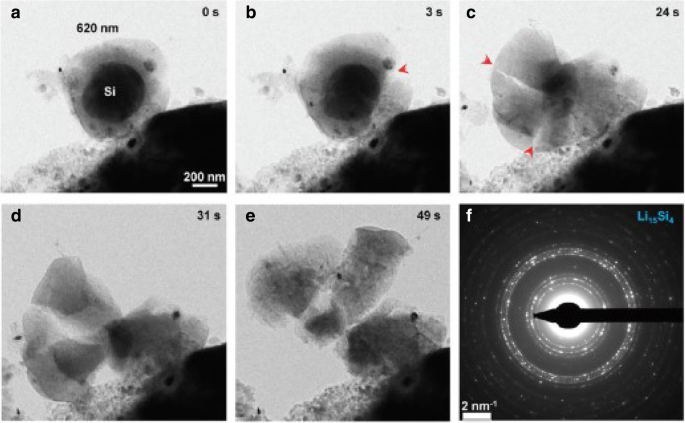
Déformation rapide d'un SiNP autonome de 620 nm pendant la lithiation chimique en 1 min. un –e Séquence temporelle de l'initiation et de la croissance des fissures. f EDP ​​indiquant la formation de Li₁₅ polycristallin Si₄ comme phase entièrement lithiée

La figure 4 montre la distribution spatiale de J _H /J _G dans une électrode Si sphérique à différents SOC en fonctionnement galvanostatique avec différents j . Sur la figure 4, les lignes continues coïncident presque avec les triangles, ce qui indique que différentes expressions de potentiel chimique ont un léger effet sur le rapport de J _H et J _G . Il est évident que la plage des valeurs de J _H /J _G augmente avec l'augmentation du courant de charge. En effet, le courant de charge plus important entraîne des taux de déformation plus élevés et, par conséquent, un impact plus important des différentes expressions du potentiel chimique. Le rapport est toujours supérieur à 1 au centre et inférieur à 1 en surface. Cela suggère que le flux obtenu à partir de l'expression développée du potentiel chimique à la surface est plus important que celui obtenu à partir de l'expression traditionnelle, alors que l'inverse est vrai au centre. Nous remarquons que toutes les lignes pleines et les triangles de la figure 4 se coupent presque avec un point. De plus, le rapport correspondant à l'intersection est toujours d'environ 1 quel que soit le courant avec lequel l'électrode est chargée. Cela suggère qu'il existe un rayon critique où le flux est moins affecté par les différentes expressions de potentiel chimique. Nous l'appelons la région indépendante du potentiel chimique (CIR). De toute évidence, le CIR est toujours près de la surface de l'électrode sphérique et est plus proche de la surface à mesure que le courant de charge augmente.

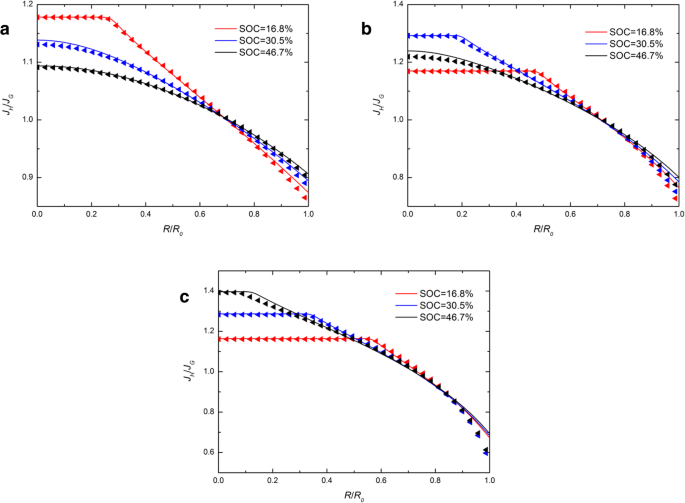
Distribution spatiale de J _H /J _G dans une électrode de nanoparticules de Si sphérique à différents SOC sous opération galvanostatique avec (a ) j =0.5j ₀ , (b ) j =j ₀ , et (c ) j =1.5j ₀ (les lignes pleines représentent les résultats avec l'expression traditionnelle du potentiel chimique; les lignes triangulaires représentent les résultats avec l'expression développée du potentiel chimique)

En comparant les potentiels chimiques traditionnels et développés dans l'équation. (26) et éq. (29), on trouve que la contrainte hydrostatique de Cauchy σ_m est la clé de la différence entre ces deux expressions. Afin d'étudier les causes du CIR, la distribution spatiale de σ_m /E dans une électrode Si sphérique à différents SOC sous fonctionnement galvanostatique avec différentes expressions de potentiel chimique sont donnés sur les figures 5 et 6. De toute évidence, presque toutes les courbes se coupent en un point du CIR et de la contrainte hydrostatique de Cauchy σ _m est proche de 0 en ce point, sauf en début de charge (SOC =6,2%). Il indique que σ_m en CIR est maintenu à un niveau bas (près de 0) pendant la majeure partie de la période de charge. On peut interpréter que les deux expressions de potentiel chimique sont presque équivalentes lorsque la contrainte hydrostatique σ_m est proche de 0. Cela peut expliquer en partie pourquoi le CIR apparaît, mais ce n'est pas suffisant pour expliquer les caractéristiques des courbes sur σ_m . Il doit être résolu par nos prochaines recherches.

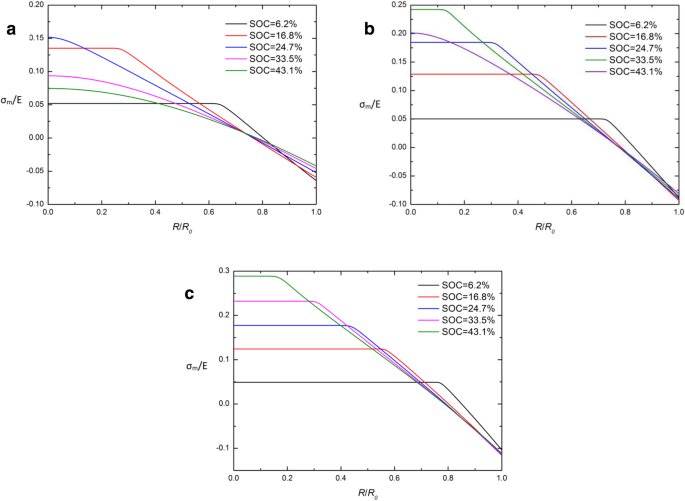
Distribution spatiale de σ _m /E dans une électrode sphérique à nanoparticules de Si à différents SOC sous opération galvanostatique avec l'expression traditionnelle du potentiel chimique et (a ) j =0.5j ₀ , (b ) j =j _0, et (c ) j =1.5j ₀

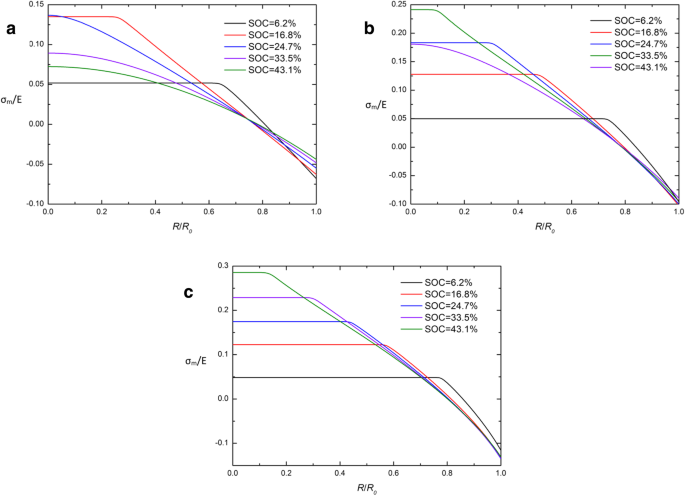
Distribution spatiale de σ _m /E dans une électrode de nanoparticules de Si sphérique à différents SOC sous opération galvanostatique avec l'expression développée du potentiel chimique (a ) j =0.5j ₀ , (b ) j =j ₀ , et (c ) j =1.5j ₀ s

Conclusions

Dans ce travail, une expression développée du potentiel chimique est proposée sans l'hypothèse de faible taux de déformation, distincte de l'expression développée qui est largement utilisée à l'heure actuelle. La différence entre les expressions traditionnelles et développées du potentiel chimique sur les distributions de contrainte et de concentration dans les électrodes à nanoparticules de Si est discutée dans les opérations potentiostatiques et galvanostatiques.

Le résultat révèle que l'effet causé par différentes expressions du potentiel chimique peut être négligé en fonctionnement galvanostatique, mais il est significatif en fonctionnement potentiostatique. On constate que l'effet est simplement lié au taux de déformation plutôt qu'à la déformation, et il peut être plus important avec l'augmentation du taux de déformation. Compte tenu de l'hypothèse de faible taux de déformation dans l'expression du potentiel chimique traditionnel, on pense que les résultats obtenus par l'expression du potentiel chimique développé sont plus fiables. Une région indépendante du potentiel chimique (CIR), où le flux causé par le potentiel chimique traditionnel et développé est presque le même pendant la majeure partie du processus lithié, se trouve près de la surface de l'électrode à nanoparticules. De plus, le CIR se rapproche de la surface avec l'augmentation du courant de charge. Un phénomène similaire apparaît également dans les courbes de contraintes hydrostatiques de Cauchy. La contrainte hydrostatique de Cauchy σ_m maintient un niveau constant et maintenu à un niveau bas (près de 0) dans le CIR au maximum, quelle que soit l'expression de potentiel chimique utilisée. De tels résultats n'ont pas encore été rapportés dans la littérature.

Disponibilité des données et des matériaux

Les ensembles de données analysés au cours de la présente étude sont disponibles auprès de l'auteur correspondant sur demande raisonnable.

Abréviations

CIR :

Une région où le flux de diffusion causé par ces deux expressions de potentiel chimique est presque le même