Modulation améliorée par résonance couplée pour un absorbeur de métamatériau chargé de graphène

Contexte

Les absorbeurs de métamatériaux plasmoniques (PM) fonctionnent avec des nanostructures métalliques à une échelle inférieure à la longueur d'onde profonde. Des absorptions parfaites peuvent être obtenues et adaptées à des longueurs d'onde particulières, conduisant à une variété d'applications, notamment émetteur/détecteur de lumière, capteur, thérapie photothermique, interaction optique-mécanique et imagerie hyperspectrale [1,2,3,4,5,6,7 ]. Les absorbeurs de particules fournissent également une plate-forme prometteuse pour la conception de nouveaux dispositifs fonctionnels dotés de propriétés ajustables. En introduisant des composants tels que des cristaux liquides, des semi-conducteurs ou des matériaux à changement de phase, la réponse optique peut être modulée électriquement, optiquement ou thermiquement [8,9,10,11,12,13], ce qui permet de nouveaux types de modulateurs, commutateurs , et des détecteurs multispectraux.

Plus récemment, le graphène a reçu une attention considérable en raison de sa capacité de modulation à grande vitesse et de son accordabilité en tant que matériau plasmonique [14,15,16,17,18,19,20]. Plus précisément, la conductivité du graphène dépend du niveau de Fermi (E _F ) qui peut être réglé en continu via une tension de polarisation en quelques nanosecondes, permettant un taux de modulation élevé dans les régions proche infrarouge et moyen infrarouge [17, 19, 20, 21, 22, 23, 24]. Cependant, comme la seule couche de graphène n'est qu'atomiquement épaisse, l'interaction entre la lumière incidente et la résonance plasmonique est assez faible. Et cette interaction devient encore plus faible dans l'infrarouge moyen en raison du blocage de Pauli des transitions interbandes [22]. En conséquence, la plage d'accord de longueur d'onde ainsi que la profondeur de modulation sont assez limitées. Le décalage de longueur d'onde est généralement inférieur à 10 % de la longueur d'onde de résonance [21, 22, 25, 26, 27, 28], ce qui reste un défi pour les applications pratiques dans les communications optiques et les détections spectrales à large bande. Ainsi, afin d'obtenir une modulation électro-optique efficace, l'interaction graphène-lumière doit être considérablement renforcée. Certains progrès ont été réalisés dans des études antérieures. Sur la base des conceptions de nanostructures complexes telles que les nano-antennes et les résonateurs en anneau fendu [19, 21, 22, 25, 27, 28], l'amélioration de l'interaction graphène-lumière a été démontrée théoriquement et expérimentalement. Pourtant, ces conceptions sont généralement compliquées ou dépendantes de la polarisation, la plage de fréquence de travail est relativement petite et la possibilité d'accord est encore limitée.

Dans ce travail, nous avons proposé un absorbeur chargé de graphène avec une plage de modulation de 9 à 14 m, ce qui est d'un grand intérêt pour des applications telles que la détection biochimique et l'imagerie thermique [5, 29, 30, 31]. Les résonances couplées à l'intérieur de la fente en forme de croix offrent quatre ordres d'amélioration du champ électrique, intensifiant fortement l'interaction graphène-lumière et entraînant un décalage allant jusqu'à 25 % dans la longueur d'onde centrale. De plus, nous proposons un modèle de circuit LC simple qui explique et prédit bien la modulation induite par le graphène contrôlée par la tension et les paramètres géométriques. Une telle plage d'accordabilité serait prometteuse dans de nombreuses applications.

Méthodes

Comme le montre la figure 1a, des patchs métalliques à motifs sont disposés avec une période de = 8 μm sur le substrat métallique séparés par un espaceur diélectrique. Une seule couche de graphène prend en sandwich entre les patchs et l'espaceur. Le substrat est très épais et agit comme un miroir réfléchissant. L'épaisseur de la couche d'espacement est t _d = 520 nm et celui des patchs métalliques est t _m = 100 nm. La figure 1b montre la vue de dessus d'une cellule unitaire. Deux sous-unités sont disposées selon une symétrie diagonale afin de supporter l'indépendance de polarisation. Une fente en forme de croix est gravée sur chaque carré, le divisant en quatre petits identiques. Les tailles des petits identiques en S ₁ et S ₂ sont l ₁ = 1.5 μm et l ₂ = 1.7 μm, respectivement. La largeur de fente pour les deux sous-unités est a = 20 nm. Dans notre étude, le matériau métallique est choisi comme l'or (Au), dont la propriété optique est décrite par le modèle de Drude de \( \varepsilon \left(\omega \right)=1-{\omega}_p^2/\left (\omega \left(\omega +\tau \right)\right) \) avec ω _p = 1.369 × 10 ¹⁶ Hz et τ = 1.224 × 10 ¹⁴ Hz [32]. L'espaceur diélectrique est composé de sulfure de zinc (ZnS), dont l'indice optique est n = 2,2 avec une perte négligeable dans l'infrarouge moyen [33].

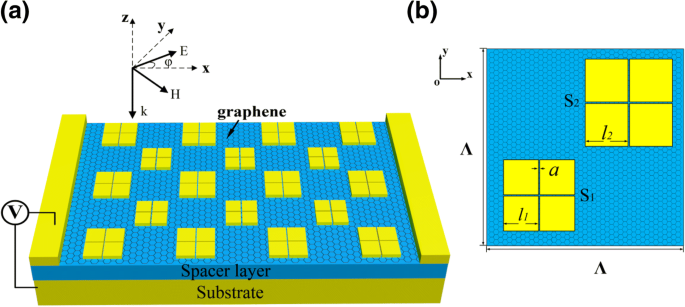
un Diagramme schématique du métamatériau proposé chargé de graphène. La fente en forme de croix dans chaque sous-unité permet une grande amélioration de l'interaction graphène-lumière sans dépendance à la polarisation. b Vue de dessus de la structure dans une période. Deux sous-unités sont disposées en diagonale avec différentes tailles de patch

La méthode du domaine temporel aux différences finies (FDTD; Lumerical FDTD Solutions) est utilisée pour calculer les spectres de réflectance et la distribution du champ électromagnétique. Les simulations sont réalisées avec des conditions aux limites périodiques dans le x et y directions et conditions de couche parfaitement appariées dans le z directions. La couche unique de graphène est modélisée comme une structure bidimensionnelle par l'approche de conductivité de surface [34]. La conductivité de surface de la couche de graphène σ _g , y compris le terme interbande σ _inter et le terme intrabande σ _intra , peut être calculé par la formule Kubo [35].

où e et ξ sont la charge et l'énergie de l'électron, ℏ est la constante de la planche réduite, ω est la fréquence angulaire, \( {f}_d\equiv 1/\left({e}^{\left(\xi -{E}_F\right)/{k}_BT}+1\right) \) fait référence à la distribution de Fermi-Dirac, T est la température absolue, Γ est le taux de diffusion, k _B est la constante de Boltzmann, et E _F est le niveau de Fermi. Dans notre calcul, T = 300 K, et Γ = 10 meV [28]. La taille du maillage près de la couche de graphène est de 0,25  nm et de 2,5  nm dans les fentes. La permittivité effective du graphène peut alors être exprimée sous la forme

où ε ₀ est la permittivité du vide, et t _g est l'épaisseur de la couche de graphène. Les équations (1) et (2) démontrent que les constantes optiques du graphène changent avec E _F . Ce changement conduit à l'accordabilité de la fréquence d'absorption, dont la plage peut être considérablement élargie par la résonance couplée dans les nanostructures, abaissant considérablement la tension appliquée dans les dispositifs.

Résultats et discussion

La figure 2a montre les spectres d'absorption pour x -onde polarisée (φ = 0) à l'incidence normale. Lorsque le niveau de Fermi est E _F = 0eV, deux pics d'absorption sont observés à la longueur d'onde λ = 12,4 μm et 13,3 μm, respectivement. La lumière incidente allant de 12,1 à 13,5  μm est presque absorbée par la nanostructure. En tant que E _F augmente, la résonance se déplace vers une longueur d'onde plus courte. À E _F = 0,2 eV, les pics d'absorption se décalent à 11,8 μm et 12,46 μm, indiquant respectivement un décalage relatif de 4,8% et 6%. Pendant ce temps, l'absorbance du pic 2 diminue, ce qui est attribué au décalage d'impédance entre le métamatériau et l'air à un E plus élevé. _F [28]. Ici, il est intéressant de noter que le pic 2 se déplace vers le bleu plus rapidement que le pic 1 alors que le niveau de Fermi continue d'augmenter. Ce comportement observé sera expliqué plus tard par un modèle de circuit.

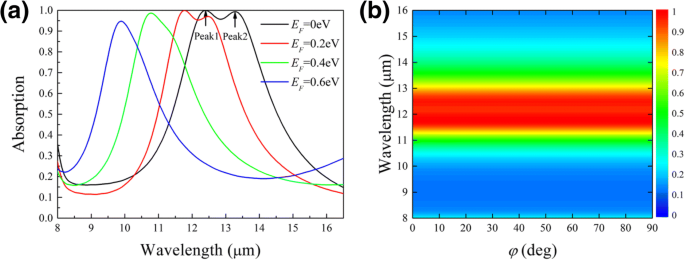
Spectres d'absorption à l'incidence normale avec différents E _F à φ = 0, montrant un grand décalage vers le bleu des pics avec l'augmentation de E _F (un ), et avec différents φ à E _F = 0.2eV, démontrant une indépendance de polarisation (b ). L'angle de polarisation φ est défini comme dans la Fig. 1a

La modulation peut être quantifiée par un paramètre M = Δλ /λ ₀ , où λ ₀ est la longueur d'onde de résonance à E _F = 0 eV et Δλ est le décalage de longueur d'onde dû au changement de E _F . La figure 2a montre M ₁ = 20,1% et M ₂ = 25,5% pour le pic 1 et le pic 2, respectivement, lorsque E _F atteint 0,6 eV. La gamme de modulation des résonances est beaucoup plus large par rapport aux travaux antérieurs [19, 21, 22, 25,26,27,28]. Une si grande modulation à un faible E _F est hautement souhaitable pour de nombreuses applications. Des calculs séparés montrent que les pics d'absorption du décalage vers le bleu avec une épaisseur décroissante de l'espaceur (Fichier supplémentaire 1). Ainsi, nous pouvons optimiser l'épaisseur pour définir un point de départ de modulation approprié. De plus, la réponse optique du métamatériau proposé est indépendante de la polarisation, comme le montre la figure 2b. Le spectre d'absorption reste inchangé lorsque l'angle de polarisation φ varie de 0 à 90°, en raison de la symétrie du design.

Le mécanisme des absorptions parfaites est clairement illustré par les distributions de champ aux résonances. En raison de la structure métal-isolant-métal (MIM) bien connue [3, 32, 36, 37, 38] illustrée sur la figure 1, des SPP localisés sont stimulés pour former des résonances magnétiques compactes dans chaque patch. Les figures 3a et b montrent le champ magnétique normalisé |H| ² dans la couche de graphène pour E _F = 0.2 eV aux longueurs d'onde de résonance de λ ₁ = 11.8 μm et λ ₂ = 12,46 μm, respectivement. Les SPP étant fortement localisés, deux sous-unités peuvent fonctionner indépendamment. Cependant, en raison de la faible largeur de la fente de séparation à l'intérieur de chaque sous-unité, les résonances des quatre identiques sont en fait couplées les unes aux autres. Et ce couplage augmente énormément le champ électrique à l'intérieur de la fente, comme le montrent les figures 3c et d. Seul le E champs dans le y -les fentes de direction sont évidentes ici car la lumière incidente est dans le x polarisation. L'intensité du E le champ amélioré par le couplage de résonance est de quatre ordres de grandeur plus grand que celui de la lumière incidente E _inc . En revanche, les champs les plus intensifiés utilisés pour la modulation dans les travaux antérieurs se situent aux bords des patchs. Les figures 3e et f montrent la comparaison nette des améliorations entre les fentes et les bords le long de la ligne blanche sur les figures 3c et d, respectivement.

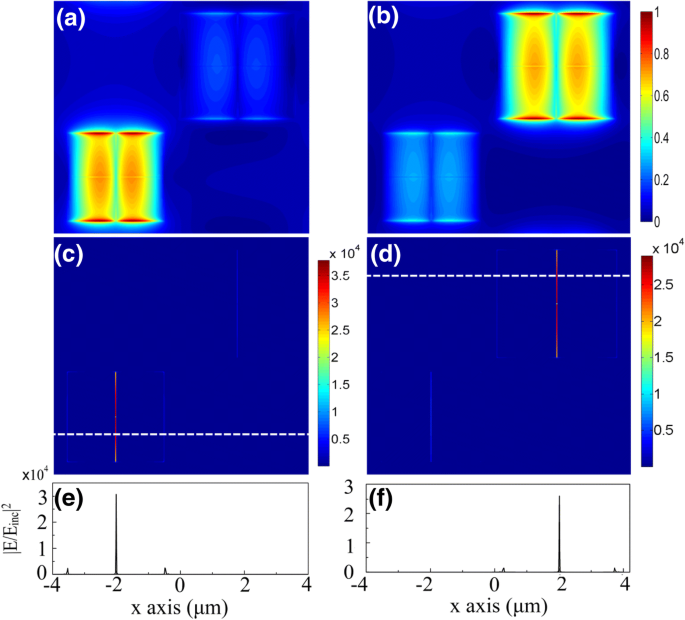
Distributions de champ dans la couche de graphène à E _F = 0,2 eV pour la lumière polarisée en x à l'incidence normale, montrant une grande amélioration dans la fente causée par les résonances couplées. a, b Champ magnétique normalisé |H| ² à λ ₁ = 11.8 μm (a ) et λ ₂ = 12,46 μm (b ); c , d La distribution de champ correspondante de |E/E_inc | ² ; e , f |E/E_inc | ² le long de la ligne en pointillés blanche indiquée en c et d , respectivement. Un contraste net est observé entre l'intensité à l'intérieur de la fente et celle sur les bords du patch, donnant des indices pour une plage de réglage beaucoup plus large que celle des travaux précédents

De telles distributions de champ expliquent bien la raison pour laquelle la modulation est si grande dans notre proposition. Sur la base d'une théorie des perturbations, le décalage de résonance induit par le graphène peut être évalué comme Δω =  − iσ _g ∫_S |E_s | ² dS /W ₀ [22]. Ici, |E_s | ² est l'intensité du champ électrique dans la couche de graphène, W ₀ est l'énergie stockée, et S désigne la zone couverte par le graphène. Le décalage spectral de la résonance (Re(Δω )) est décidé par la partie imaginaire de σ _g , ce qui est bien supérieur à sa part réelle dans le moyen infrarouge [22, 28]. Comme le montre clairement la figure 3c-f, l'amélioration du champ électrique à l'intérieur de la fente étroite est plus de 10 fois supérieure à celle des bords. En conséquence, la valeur intégrale est principalement contribuée par le E grandement amélioré champ dans les slots de patch, conduisant à un décalage beaucoup plus important des pics que dans les cas précédents qui ne possèdent que le E amélioré champs aux bords métalliques [21, 22, 25, 27, 28].

Selon les distributions de champ et les discussions ci-dessus, un modèle de circuit LC est proposé pour étudier le comportement d'accord. Comme le montre la figure 4a, L _i et C _i (i = 1, 2) sont respectivement l'inductance et la capacité du patch S _i dans la figure 1b. Lorsque la largeur de fente a est très grand et qu'il n'y a pas de couche de graphène, on peut ignorer les effets induits par les fentes et le graphène. Ensuite, L _i et C _i peut être décidé par des calculs séparés par ajustement avec la longueur d'onde de résonance obtenue dans les spectres d'absorption [37, 39, 40]. Les résultats sont L ₁ = 0,07 pH et C ₁ = 350 aF pour la sous-unité S ₁ , tandis que L ₂ = 0,075 pH et C ₂ = 380 aF pour la sous-unité S ₂ . L'effet de couplage induit par fente à l'intérieur de chaque sous-unité peut être décrit par une capacité shunt C _c , qui diminue avec l'augmentation de la largeur de fente a . Dans nos cas, C _c est de 290 aF pour a = 20 nm, et devient 200 aF, 180 aF et 135 aF avec chaque augmentation de 10 nm de a . La longueur d'onde de résonance est obtenue en laissant l'impédance du circuit à zéro, c'est-à-dire \( {\lambda}_i^0=2\pi {c}_0\sqrt{L_i{\mathrm{C}}_i^0} \). Ici, c ₀ est la vitesse de la lumière dans le vide, "i ” fait référence à la sous-unité S _i , et \( {C}_i^0={C}_i+{C}_c \).

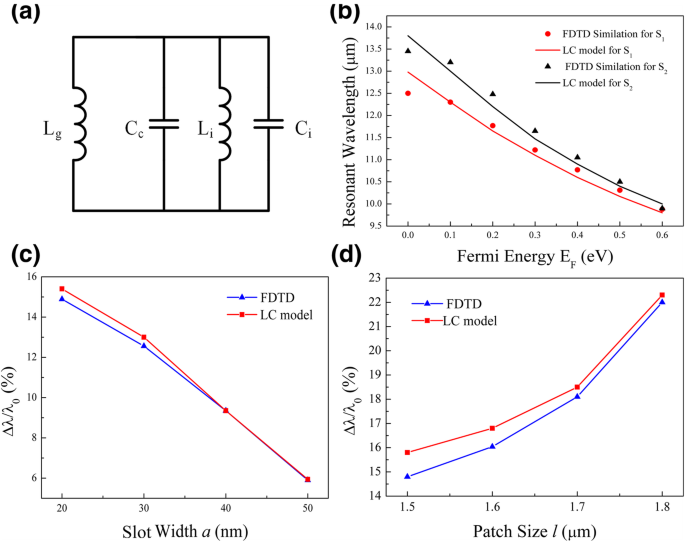
un Un modèle de circuit LC comprend des contributions de patchs séparés (L _i et C _i ), fente (C _c ), et le graphène (L _g ). b Résonances calculées par le modèle LC par rapport aux simulations FDTD. c , d Décalage de résonance pour un seul patch à E _F = 0.4 eV avec un paramètre géométrique changeant de c largeur de fente (l = 1.5 μm) et d taille du patch (a = 20 nm)

La couche de graphène bidimensionnelle agit essentiellement comme un inducteur. Comme le montre la figure 3, la principale contribution de la couche de graphène provient de la position de la fente où le champ électrique est intensifié. Étant donné que la largeur de fente est beaucoup plus petite que la longueur d'onde de fonctionnement et la longueur d'onde du plasmon de graphène, l'approximation quasi-statique est valide. La tension V et le I actuel à travers la fente peut être évalué par V = aE etJe = 2l _je t _g (σ _g − iωε ₀ )E , où E est le champ électrique dans la couche de graphène. On peut donc introduire une inductance L _g =  − 1/ω Im(V/I) [41], qui décrit la contribution de la couche de graphène et s'avère être

Cet inducteur sert d'élément parallèle représenté sur la figure 4a. En conséquence, l'inductance totale d'un patch est obtenue par \( 1/{L}_i^{\prime }=1/{L}_i+1/{L}_{\mathrm{g}} \). La longueur d'onde de résonance finale de chaque sous-unité, avec la couche de graphène, devient

Parce que chaque sous-unité fonctionne indépendamment, l'impédance totale du métamatériau peut être obtenue à partir de la connexion en parallèle des impédances des deux sous-unités.

Ce modèle LC prédit un décalage vers le bleu de la résonance avec l'augmentation de E _F . Déduit des Éqs. (1) et (2), on obtient une valeur plus grande de |Re(ε _g )| pour le graphène à un E plus élevé _F , ce qui donne un L plus petit _g dans l'éq. (3). En raison de la connexion parallèle des inducteurs, l'inducteur final \( {L}_i^{\prime } \) devient plus petit, conduisant à une longueur d'onde de résonance plus courte dans l'équation. (4). Le résultat calculé est résumé sur la figure 4b, montrant un bon accord avec la longueur d'onde de résonance obtenue par les simulations FDTD. Une petite déviation est observée car notre modèle LC ignore la contribution des champs faibles aux bords de chaque patch (Fig. 3c–f). Le modèle LC montre également comment les paramètres géométriques influencent le décalage vers le bleu de la résonance. Différencier l'équation. (4), nous avons \( \partial {\lambda}_i^{\prime }/\partial {L}_i^{\prime}\propto 1/\sqrt{L_i^{\prime }} \). Il est évident qu'une petite valeur de \( \sqrt{L_i^{\prime }} \) est privilégiée pour augmenter la sensibilité de ce décalage vers le bleu. Parce que les inducteurs sont connectés en parallèle et L _i est fixe, une petite valeur de l'inductance totale \( {L}_i^{\prime } \) signifie une petite valeur de l'inductance du graphène L _g . Afin d'augmenter la plage de réglage, la largeur de fente a doit être petit et la taille du patch l être grand, selon l'éq. (3). La figure 4c montre que le décalage vers le bleu de la résonance à E _F = 0.4 eV augmente d'environ 6 à 15%, lorsque la largeur de la fente à l'intérieur de S ₁ diminue de 50 à 20  nm. En revanche, si l'on fixe la largeur de la fente à a = 20 nm, la résonance augmente de 15 à 22% avec la taille du patch changeant de 1,5 à 1,8 μm, comme le montre la Fig. 4d. Le bon accord avec les simulations FDTD démontre qu'un modèle de circuit aussi simple est une méthode efficace pour étudier les dispositifs de métamatériaux associés.

Conclusions

En conclusion, nous avons conçu un absorbeur de métamatériau à large bande indépendant de la polarisation avec une large gamme de modulation. Pour les deux résonances, la plage d'accord atteint jusqu'à 20,1% et 25,5% de la longueur d'onde centrale lorsque E _F augmente de 0 à 0,6 eV. Une modulation aussi importante provient de l'interaction graphène-lumière considérablement améliorée par les résonances couplées à l'intérieur de la fente en forme de croix de chaque patch métallique. Cet effet est bien décrit par un inducteur introduit par le graphène dans le modèle LC. Un modèle aussi simple prédit le comportement de modulation sous différents paramètres géométriques, et les résultats concordent bien avec les simulations FDTD. Notre proposition est bénéfique pour des applications potentielles telles que la communication optique, la détection et l'imagerie thermique.

Abréviations

E _F :

Niveau de Fermi

FDTD :

Domaine temporel différent fini

MIM :

Métal-isolant-métal

MP :

Métamatériau plasmonique

ZnS :

Sulfure de zinc