Détection de l'excitation spatialement localisée dans les superréseaux à points quantiques InAs/InGaAs auto-organisés :un moyen d'améliorer l'efficacité photovoltaïque

Contexte

Les points quantiques auto-assemblés (QD) ont été largement étudiés pour des applications possibles en optoélectronique en raison de la nature du confinement tridimensionnel des porteurs et de la densité d'états de type . Récemment, des structures QD ont été proposées pour réaliser les cellules solaires à bande intermédiaire (IBSC), qui introduisent des photo-porteurs supplémentaires à travers les absorptions des bandes de valence-IB et de conduction IB [1]. Les IBSC à base de GaAs avec des QD qui ont une bande interdite d'énergie plus petite que GaAs forment des structures en tandem capables d'absorber des photons à des énergies inférieures à la bande interdite de GaAs, ce qui entraîne des rendements de conversion d'énergie plus élevés [2]. La formation de la bande intermédiaire QD nécessite une structure multicouche compacte de QD haute densité [3, 4]. Cependant, la qualité cristalline des QD InAs se dégrade à mesure que le nombre de couches QD augmente et que l'espacement des couches diminue en raison de l'accumulation de contrainte de compression interne. La contrainte excessive induira des dislocations et des défauts qui s'enfilent des QD vers la surface. Par conséquent, les performances d'un QD SC InAs/GaAs se dégradent également à mesure que le nombre de couches QD augmente [5]. Pour surmonter ces problèmes, une technique de croissance par compensation de contrainte a été démontrée avec des couches tampons GaAsN, GaAsP et GaP pour les systèmes de matériaux InAs/GaAs [6,7,8]. Une autre technique pour surmonter ces problèmes consiste à recouvrir la couche QDs d'InAs/GaAs d'une fine couche d'InGaAs à contrainte réduite. Par rapport aux QD InAs/GaAs, cette couche provoque un décalage vers le rouge de la photo-réponse en raison de la présence d'un petit décalage de maille entre InAs et InGaAs. L'étude de photoluminescence dépendante de la température fournit des informations utiles sur les QDs SC multi-empilés InAs/GaAs qui sont d'un intérêt pratique et théorique considérable. Classiquement, la bande interdite d'un matériau semi-conducteur diminue de façon monotone avec l'augmentation de la température. Des matériaux spéciaux, tels que les QD InAs/GaAs, ont montré une anomalie dans le PL à basse température en raison de mécanismes de transfert de porteurs activés thermiquement au sein de l'ensemble des points quantiques. Cependant, ces anomalies disparaissent progressivement après les processus de mélange post-croissance dans les hétérostructures InAs/InGaAs/GaAs QD comme le montrent Ilahi et al. [9]. Des hétérostructures similaires à celles de la présente étude ont été étudiées pour leur efficacité dans les applications photovoltaïques par Sayari et al. [dix]. De nombreux modèles ont été proposés au cours des dernières décennies, comme celui de Passler, Vina et Varshni. Afin de produire des dispositifs fiables, le comportement en température de ce type d'hétérostructures QD InAs/InGaAs/GaAs doit être bien compris et ceci en utilisant le modèle le mieux adapté. Nous utilisons ici le modèle classique de Passler corrigé du coefficient de redistribution thermique, afin de mieux comprendre la dépendance thermique observée en forme de S de la bande interdite excitonique. Notre étude donne lieu à une image précise et cohérente de la localisation et du transfert des porteurs dans une hétérostructure QD InAs/InGaAs/GaAs, qui est un matériau énergétique extrêmement important sur le plan technologique pour la fabrication de dispositifs photovoltaïques à haut rendement.

Détails expérimentaux

La figure 1 illustre un diagramme schématique de l'hétérostructure QD InAs/InGaAs/GaAs étudiée dans notre étude. L'hétérostructure se compose de cinq empilements de InAs/In_0.11 Ga_0,89 Couches As/GaAs QD prises en sandwich par une couche intrinsèque de GaAs de 80 nm. Les couches épitaxiales ont été cultivées sur épiready n ⁺ -Substrat GaAs (100) utilisant l'épitaxie par faisceau moléculaire à source solide (SS-MBE) avec le système Riber MBE 32P. Après désorption d'oxyde, un n ⁺ de 250 nm -tampon GaAs dopé avec une densité de dopage de 2 × 10 ¹⁸ cm ⁻³ a été cultivé à 520 °C suivi d'une couche de base de GaAs dopé n à 1000 nm avec une densité de dopage de 10 ¹⁷ cm ⁻³ . La température du substrat est ensuite abaissée et stabilisée à 500 °C pour le dépôt de la région intrinsèque. Comme le montre la figure 1, les couches répétées sont constituées de 2,5 monocouches (ML) de couverture InAs, de 5 nm d'épaisseur In_0,11 Ga_0,89 As et GaAs de 33 nm d'épaisseur. La formation des QDs a été contrôlée in situ en surveillant le diagramme de diffraction des électrons de haute énergie (RHEED). Le but du In_0.11 de 5 nm d'épaisseur Ga_0,89 As est de décaler vers le rouge les spectres d'émission et d'absorption, tandis que le GaAs de 33 nm d'épaisseur agit comme une couche d'espacement. Les taux de croissance pour InAs, In_0.11 Ga_0,89 Les couches d'As et de GaAs étaient respectivement de 0,08 ML/s, 0,78 ML/s et 0,7 ML/s, mesurées par les oscillations de spot spéculaire RHEED. Au final, une couche émettrice de GaAs dopé p à 500 nm (2 × 10 ¹⁷ cm ⁻³ ) suivi d'un GaAs 100 nm p ⁺ -couche de contact dopée (5 × 10 ¹⁸ cm ⁻³ ) ont été cultivés au-dessus de l'hétérostructure. Le silicium (Si) et le béryllium (Be) ont été utilisés comme dopants de type n et p, respectivement. Pendant la croissance, la température a été calibrée par un pyromètre.

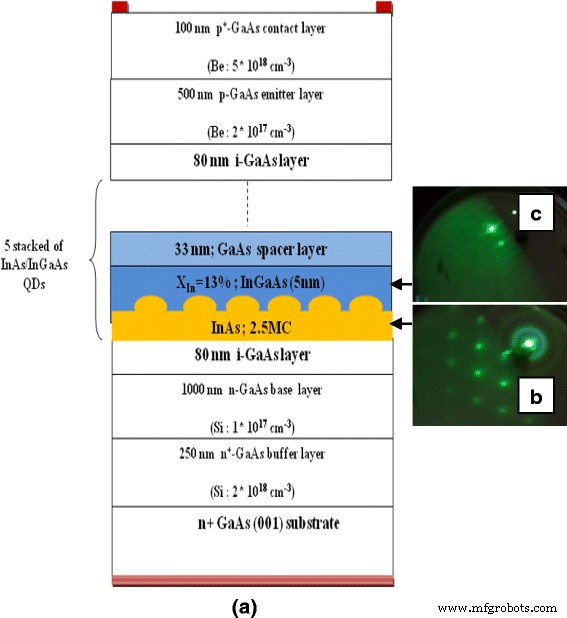
un Structure schématique en couches des QDs SC InAs/InGaAs empilés à cinq couches développées sur (001) n ⁺ -Substrat GaAs. b RHEED modelé après la croissance de 2,5 ML d'InAs (croissance tridimensionnelle). c RHEED modelé pendant la croissance de 5 nm d'InGaAs (croissance bidimensionnelle) [10]

L'ellipsométrie spectroscopique (SE) a été réalisée à température ambiante entre 1 et 6 eV, à l'aide d'un appareil J.A. Ellipsomètre spectroscopique à angle variable Woollam (VASE) M-2000. Les mesures SE ont été effectuées à des angles d'incidence allant de 45° à 60°. Dans les mesures PL, un ion argon (Ar ⁺ ) un laser d'une longueur d'onde de 514,5 nm a été utilisé comme source d'excitation pour générer des paires électron-trou. La lumière de luminescence des échantillons a été dispersée par un spectromètre à haute résolution et détectée par un photodétecteur Ge refroidi thermoélectriquement avec un amplificateur intégré. Pour les mesures PL dépendantes de la puissance d'excitation et de la température, les échantillons ont été montés dans un cryostat à hélium à cycle fermé et à température contrôlée. Les spectres PL ont été pris dans la plage de puissance de sortie nominale de 1,5 à 350 mW et la plage de températures de 11 à 300 K. Les mesures de PL résolues dans le temps ont été effectuées dans un hélium à température variable (10 à 240 K), à cycle fermé. cryostat. La raie à 514 nm a été utilisée comme longueur d'onde d'excitation, à partir d'un laser à impulsions picoseconde Ti :saphir à mode verrouillé à une fréquence de répétition de 80 MHz avec une largeur d'impulsion de 1,2 ps.

Résultats et discussions

La figure 2 montre les parties réelles (a) et imaginaires (b) mesurées de la fonction diélectrique de l'hétérostructure QD InAs/InGaAs/GaAs à 300 K pour la plage d'énergie 1 à 6 eV. Les parties réelles et imaginaires suivent des schémas différents. La variation de la fonction diélectrique avec l'énergie des photons indique que certaines interactions entre les photons et les électrons dans les films sont produites dans la plage d'énergie de 1 à 6 eV. Les deux principales caractéristiques spectrales sont le E₁ et E₂ structures de point critique (CP) à ~3 et ~4,5 eV, respectivement [11, 12]. Pour déterminer quantitativement la position énergétique des différentes transitions interbandes, nous avons pris le passage par zéro du spectre de dérivée seconde de la partie imaginaire de la fonction pseudodiélectrique. Les différentes énergies de transition obtenues sont résumées dans le tableau 1.

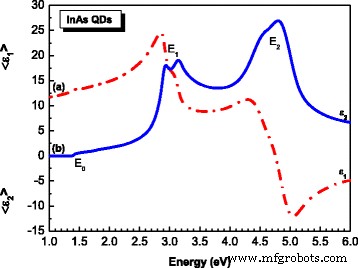
Réel (ϵ ₁ ) (ligne rouge pointillée ) et imaginaire (ϵ ₂ ) (ligne bleue continue ) parties de fonctions diélectriques de l'hétérostructure InAs/InGaAs QD obtenues à partir de mesures SE [10]

La figure 3 montre le deuxième spectre de dérivée d'énergie de la partie imaginaire de la fonction pseudodiélectrique illustrée à la figure 2. Les deux pics à 2,9 et 3,1 eV correspondent, respectivement, au E ₁ et E ₁ + Δ₁ , transitions interbandes dans GaAs. Cependant, les deux pics rapprochés à environ 4,4 et 4,7 eV sont causés par les transitions CP E ₀ ' et E ₂ , respectivement, dans les couches InAs QD [12]. Notons que la contribution du E ₁ + Δ₁ Énergie CP (2,74 eV) [12] de l'InAs au E ₁ un (2,91 eV) [11] de GaAs ne peut être exclu en raison de la faible différence entre les deux valeurs d'énergie. A basse énergie, la bande interdite de GaAs est clairement distinguable dans le ε spectre à environ 1,4 eV. De plus, le deuxième spectre de dérivée d'énergie (Fig. 3) montre une transition interbande à 1,75 eV qui correspond au E ₀ + Δ₀ CP énergie de GaAs [11]. On sait que ε ₂ est une jauge et une mesure de la qualité des matériaux ; la valeur la plus élevée implique l'interface la plus abrupte [13]. Selon la littérature, ε ₂ des valeurs d'environ 25, la valeur la plus élevée étant dans notre cas 26,8, obtenues dans la région du E ₂ bande interdite proche de 4,7 eV, indique la haute qualité des matériaux formant l'hétérostructure QD InAs/InGaAs/GaAs développée par SS-MBE.

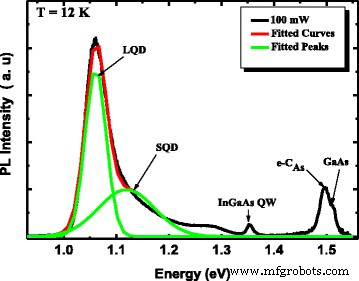
Spectre de dérivée seconde de la partie imaginaire (ϵ ₂ ) de la fonction diélectrique en fonction de l'énergie des photons pour l'hétérostructure InAs/InGaAs QD. Les énergies de transition issues des couches InAs QD et GaAs sont indiquées [10]

La figure 4 montre le spectre PL de la région active dans l'hétérostructure QD InAs/InGaAs/GaAs avec une puissance d'excitation de 100 mW à basse température (12 K). De toute évidence, le spectre présente une forme asymétrique située du côté des hautes énergies et qui peut être déconvoluée en deux sous-bandes par ajustement gaussien [14]. Compte tenu de la dépendance des potentiels de confinement quantique sur la taille du point, le pic le plus intense situé à 1,06 eV est attribué à l'émission des états fondamentaux de plus grands QD (LQD), tandis que le pic d'énergie le plus élevé à 1,11 eV fait référence à l'émission de les états fondamentaux des plus petits QD (SQD) [15]. Ainsi, à très faible puissance d'excitation et à basse température, on en déduit que la forme asymétrique est due à la luminescence provenant d'une distribution bimodale de la taille des points [16]. De plus, les pics provenant de la couche de puits quantique d'InGaAs, la recombinaison entre les électrons de la bande de conduction GaAs et les trous au niveau de l'accepteur de carbone (e-C_As ) [17] et la bande interdite GaAs sont observées autour de 1,35, 1,49 et 1,51 eV, respectivement. Pour confirmer cette attribution à la forme asymétrique, nous avons effectué des mesures PL à différentes puissances laser allant de 10 à 100 mW. Nous avons également effectué des mesures AFM sur une structure non coiffée similaire à celle étudiée. D'après la figure 5, il est clair que l'hétérostructure a une forme PL indépendante de la puissance. En dehors du spectre d'excitation le plus élevé, l'intensité PL et la largeur de raie du pic PL à haute énergie de l'hétérostructure ne sont pas significativement modifiées. De plus, la séparation d'énergie entre les deux pics PL (Fig. 5) est d'environ 50 meV. Comme prévu, l'image AFM démontre que les QD de la cinquième couche possèdent une distribution de taille bimodale avec une densité totale de QD de 7 × 10 ¹⁰ cm^(−2). En supposant que les pics latéraux à basse énergie de l'hétérostructure correspondent à l'état fondamental des grands QD (LQD), nous pouvons dire que les pics à haute énergie à haute puissance semblent être le résultat des états fondamentaux des QD relativement petits (SQD ).

Spectre PL mesuré à basse température (12 K) à partir de l'hétérostructure QD empilée à cinq couches InAs/InGaAs. Une analyse de forme de ligne des spectres prouve que le signal QD PL est une convolution de deux pics de forme gaussienne, comme indiqué par les lignes pleines

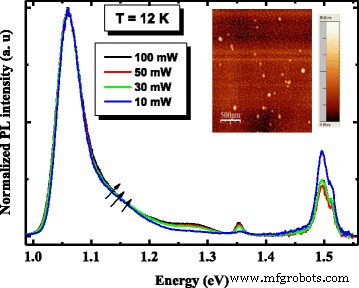
Spectres PL normalisés dépendant de la puissance d'excitation de l'hétérostructure QD InAs/InGaAs mesurés à 12 K

Pour avoir un aperçu des mécanismes de recombinaison PL, des mesures PL dépendantes de la température sont effectuées sur l'hétérostructure de 10 à 300 K et représentées sur la figure 6. La figure 7 montre la position de l'énergie PL du pic principal associé à l'émission des LQD. Ce pic montre une dépendance anormale de la température entre 10 et 100 K par rapport à d'autres alliages ternaires III-V tels que le GaAlAs conventionnel [18]. Dans cette plage de température (région (i)), un décalage vers le rouge d'environ 12 meV est observé. Ce décalage est dû à la recombinaison des excitons via les états localisés au sein de l'ensemble des LQD distribués de manière inhomogène. Au fur et à mesure que la température augmente dans cette plage de températures, les porteurs sont activés thermiquement et transférés des plus petits aux plus grands QD au sein de l'ensemble, où ils se recombinent finalement par rayonnement. Cela rend les phénomènes observés susceptibles de provenir de la grande dispersion de la taille des points dans notre structure (voir encadré AFM). La température caractéristique à laquelle les deux processus de recombinaison (porteuses localisées et délocalisées) participent à parts égales au signal PL est notée T _loc/deloc . Ensuite, entre 100 et 120 K (région (ii)), l'énergie de crête augmente. Cela est dû à la fuite des porteurs des états les moins profonds vers les états supérieurs. La température caractéristique est notée T _échapper . Même à haute température (région (iii)), les excitons sont totalement délocalisés et une recombinaison bande à bande est récupérée.

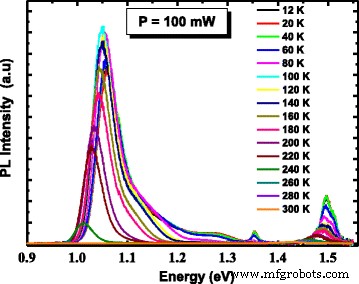
Spectres PL dépendant de la température de l'hétérostructure InAs/InGaAs QD mesurés à une puissance d'excitation de 100 mW

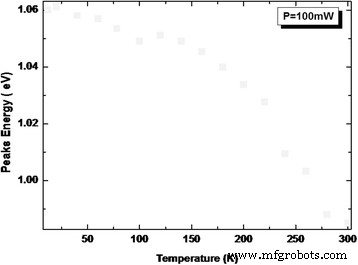
Energies de crête LQD PL de l'hétérostructure InAs/InGaAs QD étudiée mesurées à différentes températures

Pour mieux comprendre le processus de recombinaison dans les QD multi-empilés InAs/InGaAs/GaAs, nous avons étudié le PL résolu en temps en utilisant la technique de photocomptage corrélée dans le temps. Il a été prédit théoriquement que la durée de vie de désintégration des excitons des QD est sensible à la température [19]. Des mesures expérimentales ont montré que les durées de vie sont bien une constante de température inférieure à une température critique [20]. Markus et al. [21] ont signalé une durée de vie constante d'environ 950 ps sur une large plage de températures dans les limites de l'erreur expérimentale.

La figure 8a présente le spectre de décroissance PL, compris entre 17 et 240 K pour une énergie de détection fixée à 1,06 eV et une énergie d'excitation (λ _sauf = 514 nm). Ces spectres sont bien ajustés théoriquement par une fonction mono-exponentielle, avec un temps de décroissance d'environ 1000 ps à basse température. Ce temps de décroissance lent, comparé aux films minces semi-conducteurs III-V [22], est une signature de la présence d'états localisés [23], et la recombinaison des porteurs au pic LQD devrait être purement radiative. En effet, à basse température, les électrons et trous photo-générés, avant de se recombiner, mettent du temps à former des excitons et relâchent leur énergie pour être capturés par les états localisés peu profonds. Ces phénomènes conduisent à un temps de décroissance lent. L'effet de la température sur le temps de décroissance de la PL a été étudié et montre la présence de deux régimes différents comme représenté sur la Fig. 8b [24]. Nous remarquons que le temps de décroissance associé à l'énergie inférieure de la bande PL (LQD (1,06 eV)) est presque constant (1000 ps) jusqu'à 140 K, puis, il diminue à mesure que la température augmente.

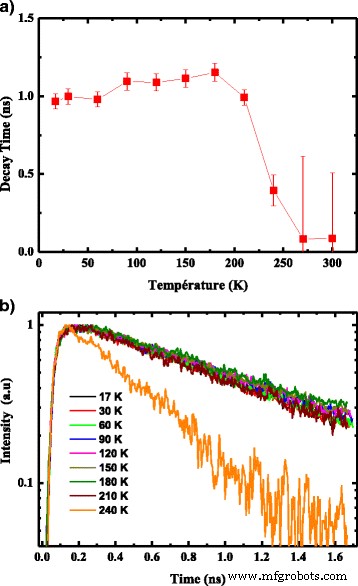
un Temps de décroissance du pic LQD en fonction de la température de l'échantillon pour une longueur d'onde d'excitation de 514 nm. b Intensité typique de décroissance de la photoluminescence par rapport à la température du pic LQD mesurée à une longueur d'onde d'excitation de 514 nm

Approche théorique

Afin de comprendre la dépendance anormale de la température de PL, la position du pic de PL a été étudiée à l'aide du modèle LSE développé par Li et al. [25, 26]. En effet, ce modèle quantitatif fournit une explication satisfaisante des caractéristiques spectrales anormales de la luminescence à l'état localisé précédemment observée dans plusieurs matériaux III-V tels que les alliages B(In)GaAs/GaAs [27, 28] à base de bore et InGaAs/GaAs. MQW [29, 30]. Le modèle suppose que l'état localisé a une distribution d'énergie de type gaussien pour la densité d'états donnée par :

Où σ et E _ch sont respectivement le paramètre d'élargissement pour la distribution des états localisés (profondeur de localisation) et le niveau de barrière que les porteurs doivent surmonter pour transférer. En régime quasi permanent, la dynamique des excitons localisés peut être décrite par les équations de vitesse suivantes :

Les paramètres τ _r , τ _tr , γ _c , K _B , Λ, et N ' représentent respectivement le temps de recombinaison des porteurs (durée de vie radiative), le temps de transfert des porteurs (durée de vie non radiative), le coefficient de recapture, la constante de Boltzmann, le nombre total d'états localisés et le nombre total de porteurs thermiquement activés à l'écart du états localisés. G (E ) représente le taux de génération de porteuses. La quantité \( \frac{\gamma_c N\hbox{'}\left( E, T\right)\rho (E)}{\Lambda} \) est le nombre de porteurs re-capturés par les états localisés par unité temps. Le troisième terme à droite donne le taux d'échappement thermique des porteurs localisés. Le dernier représente le taux de dépeuplement des porteurs dû à la recombinaison radiative. La densité de population de porteurs localisés est proportionnelle à la fonction de distribution et à la densité d'états des porteurs localisés. En fait, la solution de l'équation. (2) peut être décrit par l'équation. (3).

où E ₀ est l'énergie centrale. Mathématiquement, la dépendance à la température de la position du pic due à la redistribution thermique du porteur dans les états localisés déterminés à partir de \( \frac{\partial N\left( E, T\right)}{\partial t}=0 \) est donnée par :

Où x (T ) est la solution numérique de l'équation non linéaire. (5) :

L'équation 5 n'a qu'une seule solution pour \( 0 $$ E(T)\approx {E}_0-\frac{\sigma^2}{K_B T} $$ (6)

On sait que la bande interdite d'un matériau semi-conducteur idéalisé est généralement décrite par la formule empirique de Passler [32]. Compte tenu de la correction due au coefficient de redistribution thermique, la variation de la position du pic de luminescence à l'aide du modèle LSE décrit par l'Eq. (7) :

où θ est un paramètre de température caractéristique qui devait être comparable à la température de Debye θ _D . Pour T>>θ , nous voyons que α ne représente que la limite de la magnitude de la dérivée première, \( {\frac{dEg(T)}{dT}}_{T\to \infty } \). L'exposant « p » est lié à la forme de la fonction spectrale électron-phonon sous-jacente [33]. Le modèle fournit un bon ajustement à l'évolution expérimentale qui est confirmée par la figure 9. Les paramètres d'ajustement sont résumés dans le tableau 2.

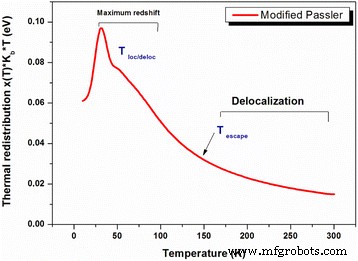
Evolution de la photoluminescence dépendante de la température du pic LQD (carrés noirs pleins ) ajusté en utilisant la loi de Passler empirique (trait plein bleu ) et la vérité de la relation de Passler modifiée au modèle LSE (ligne continue rouge )

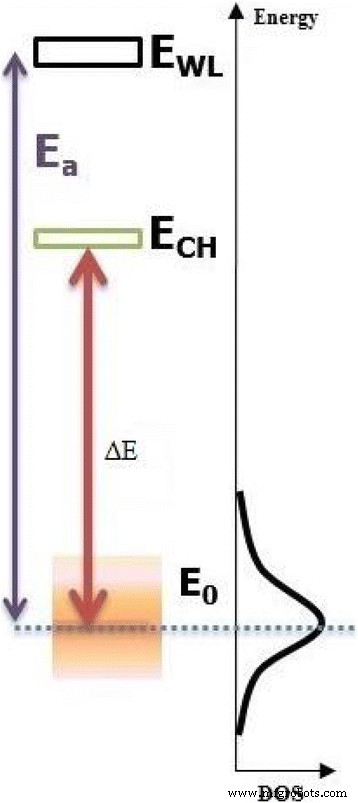
L'énergie de crête PL dépend fortement de la redistribution thermique représentée sur la figure 10. Cette dernière indique une augmentation rapide de la plage de température cryogénique. Le maximum de redistribution thermique correspond au maximum de redshift dans l'évolution de l'énergie (~50-100 K). Dans la région de haute température PL, la redistribution thermique diminue de façon exponentielle et tend à s'annuler car à partir de 150 K elle démarre le processus de délocalisation et le retour aux transitions de bande à bande. Aussi, on peut l'observer lorsque les courbes classique et modifiée sont superposées (Fig. 9). L'exposant « p » indique que la contribution des phonons acoustiques longitudinaux (LA) est plus importante que la contribution des phonons optiques longitudinaux (LO ) phonons. Cette contribution semble être dominante dans la région de haute température PL où l'émission est assistée via des phonons. Le processus de distribution bimodale ouvre un canal de couplage entre les QD qui est représenté par des états d'électrons et de trous délocalisés séparés par une énergie E _ch . L'origine de ce canal de couplage est encore sujette à controverse [34,35,36]. Cependant, le canal de couplage peut être considéré comme les états intermédiaires existant entre les états WL à deux dimensions et les états QD à zéro dimension [37]. Ainsi, on peut imaginer que les porteurs dans les états QD peuvent être plus facilement excités thermiquement vers le canal de couplage que le WL en raison de la plus petite énergie d'activation nécessaire, puis transférés vers leurs QD voisins sur une distance finie. Il apparaît comme le niveau de Fermi-Dirac dans la distribution de Fermi-Dirac. Cette énergie E _ch est plus petite que l'énergie d'activation E _un extrait du diagramme d'Arrhenius (Fig. 11). La raison pour laquelle E _un est plus grande peut s'expliquer par le fait que les porteurs ont besoin d'une plus grande énergie pour atteindre la couche de mouillage (WL) comme le montre schématiquement la Fig. 12. De plus, l'amplitude de la différence ΔE = E _ch − E ₀ joue un rôle plus important dans la détermination de la dépendance à la température anormale de la luminescence des porteurs localisés. Notons que les deux cas, E _ch − E ₀> 0 et E _ch − E ₀ < 0, existe d'un point de vue physique, mais il est généralement attribué comme énergie d'activation thermique "positive". Dans notre cas, cela implique que E _ch est de 4 meV en dessous de E ₀ dans lequel des porteurs localisés sont activés thermiquement vers des états (ou des sites dans l'espace réel) avec des énergies plus élevées. Il diminue par rapport à une seule couche InAs QD avec In_0.15 Ga_0,85 En tant que couche sous-jacente réduisant les contraintes [10]. La profondeur de fluctuation potentielle attribuée par σ est le résultat de l'inhomogénéité de la distribution de la taille des QD. La profondeur potentielle est de 19 meV. Il diminue en augmentant le nombre de stacks de InAs/In_0.11 Ga_0,89 QD As/GaAs. En conséquence, nous pouvons en déduire que la diminution de la profondeur potentielle augmente l'efficacité de la structure par rapport à la couche de QD InAs/InGaAs/GaAs étudiée par Ilahi et al. et Helmi et al. [10, 36].

Redistribution thermique dépendante de la température déterminée numériquement. Les températures caractéristiques (T _loc/deloc et T _échapper ) sont indiqués par rapport au processus de localisation-délocalisation

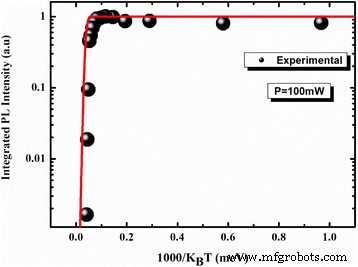
Ajustement d'Arrhenius de l'échantillon étudié. L'intensité intégrée normalisée (cercles noirs ) est doté de trois énergies d'activation (trait continu rouge )

Schéma de la distribution QD des états localisés électron/trou (exciton) (WL couche mouillante, CH canal de transfert de l'opérateur)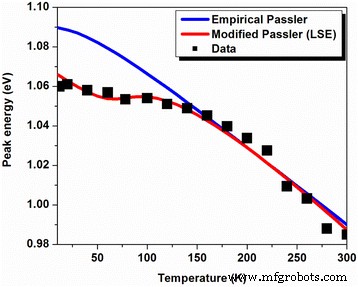

Conclusion

En conclusion, nous avons réussi à fabriquer un SC à base de GaAs avec un empilement multiple de QD InAs en coiffant une couche d'InGaAs sur les QD et en insérant des couches d'espacement GaAs. Les deux principales caractéristiques spectrales observées dans les spectres de fonctions diélectriques de l'hétérostructure QD InAs/InGaAs/GaAs à 3 et 4,5 eV sont attribuées au E ₁ et E ₂ Structures CP de GaAs et InAs, respectivement. Le spectre PL des QD InAs dans la matrice GaAs est intense et présente une forme asymétrique, ce qui indique la croissance d'une structure InAs QD multi-empilée de haute qualité. La contribution des QDs plus grands et relativement plus petits au spectre PL est également démontrée. Les mesures de luminescence ont été modélisées et réinterprétées avec succès à l'aide du modèle LSE développé. L'étude théorique a interprété quantitativement les spectres observés dépendant de la température et a mis en lumière les mécanismes complexes d'émission spontanée dans les QD InAs/InGaAs/GaAs multi-empilés, sur la base des paramètres d'ajustement. Cette étude suggère un moyen d'améliorer l'efficacité des structures QD InAs/GaAs pour leur utilisation dans des applications photovoltaïques. Ces résultats aident à améliorer la compréhension de la dynamique des porteurs dépendant de la température dans les QD d'ingénierie des déformations afin d'améliorer l'efficacité de la structure étudiée. Suite à ce travail, nous étudierons l'effet de l'orientation ainsi que l'augmentation du nombre de QD InAs/GaAs de la structure multi-stack sur la profondeur de localisation.