Quelques exemples avec des circuits CA
Connectons trois sources de tension alternative en série et utilisons des nombres complexes pour déterminer les tensions additives.
Toutes les règles et lois apprises dans l'étude des circuits à courant continu s'appliquent également aux circuits à courant alternatif (loi d'Ohm, lois de Kirchhoff, méthodes d'analyse de réseau), à l'exception des calculs de puissance (loi de Joule).
La seule qualification est que toutes les variables doit être exprimé sous une forme complexe, en tenant compte de la phase ainsi que de l'amplitude, et toutes les tensions et tous les courants doivent être de la même fréquence (afin que leurs relations de phase restent constantes). (Figure ci-dessous)
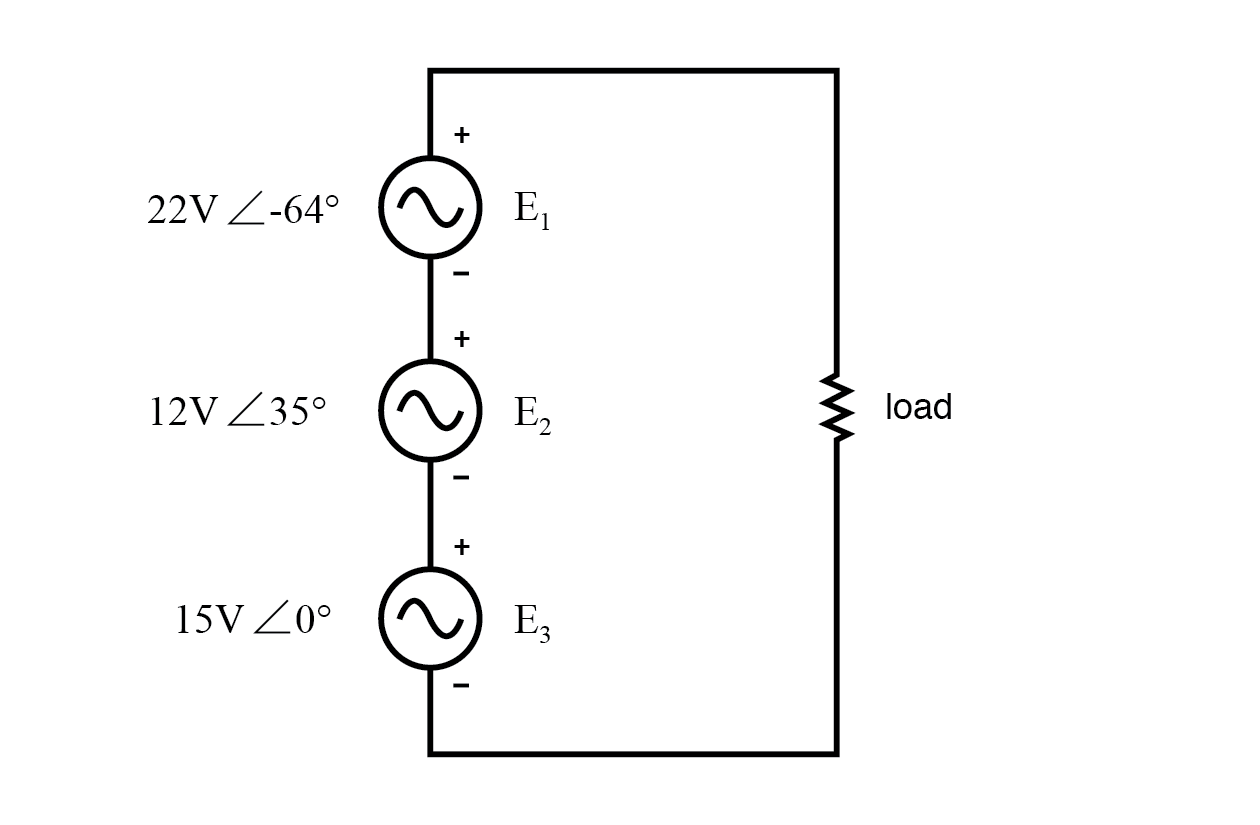
KVL permet l'ajout de tensions complexes.
Les marques de polarité pour les trois sources de tension sont orientées de manière à ce que leurs tensions indiquées s'additionnent pour former la tension totale aux bornes de la résistance de charge.
Notez que bien que l'amplitude et l'angle de phase soient donnés pour chaque source de tension alternative, aucune valeur de fréquence n'est spécifiée. Si tel est le cas, il est supposé que toutes les fréquences sont égales, répondant ainsi à nos qualifications pour appliquer les règles DC à un circuit AC (tous les chiffres sont donnés sous forme complexe, tous de la même fréquence).
La configuration de notre équation pour trouver la tension totale apparaît comme telle :
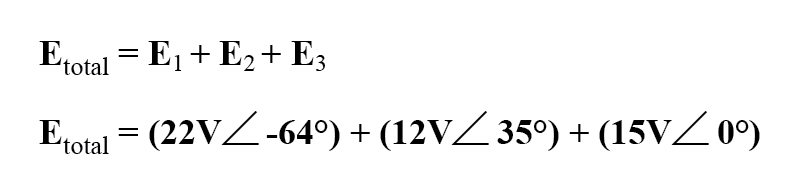
Graphiquement, les vecteurs s'additionnent comme le montre la figure ci-dessous.
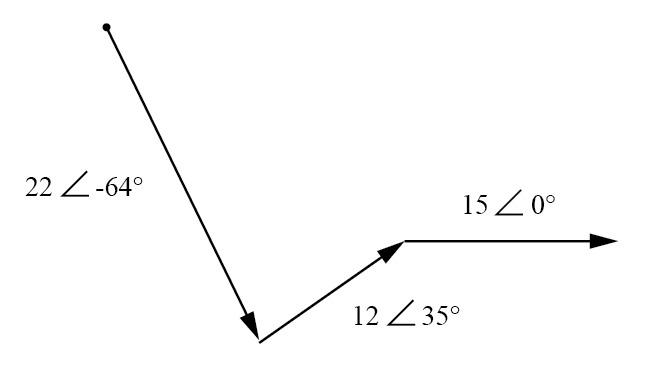
Ajout graphique de tensions vectorielles.
La somme de ces vecteurs sera un vecteur résultant provenant du point de départ du vecteur 22 volts (le point en haut à gauche du diagramme) et se terminant au point final du vecteur 15 volts (pointe de flèche au milieu -à droite du schéma) :(Figure ci-dessous)
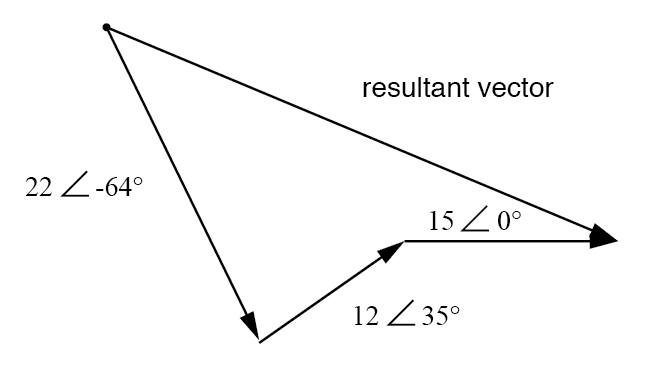
Le résultat est équivalent à la somme vectorielle des trois tensions d'origine.
Afin de déterminer la magnitude et l'angle du vecteur résultant sans recourir à des images graphiques, nous pouvons convertir chacun de ces nombres complexes de forme polaire en forme rectangulaire et additionner.
N'oubliez pas que nous ajoutons ces chiffres ensemble car les repères de polarité des trois sources de tension sont orientés de manière additive :

Sous forme polaire, cela équivaut à 36,8052 volts -20,5018°. Ce que cela signifie en termes réels, c'est que la tension mesurée sur ces trois sources de tension sera de 36,8052 volts, retardant les 15 volts (référence de phase 0°) de 20,5018°.
Un voltmètre connecté entre ces points dans un circuit réel n'indiquerait que l'amplitude polaire de la tension (36,8052 volts), pas l'angle. Un oscilloscope pourrait être utilisé pour afficher deux formes d'onde de tension et fournir ainsi une mesure de déphasage, mais pas un voltmètre.
Le même principe s'applique aux ampèremètres AC :ils indiquent la magnitude polaire du courant, pas l'angle de phase.
Ceci est extrêmement important pour relier les chiffres calculés de tension et de courant aux circuits réels.
Bien que la notation rectangulaire soit pratique pour l'addition et la soustraction et était en effet la dernière étape de notre exemple de problème ici, elle n'est pas très applicable aux mesures pratiques.
Les chiffres rectangulaires doivent être convertis en chiffres polaires (en particulier la grandeur polaire) ) avant qu'elles puissent être liées aux mesures réelles du circuit.
Nous pouvons utiliser SPICE pour vérifier l'exactitude de nos résultats. Dans ce circuit de test, la valeur de la résistance de 10 kΩ est assez arbitraire. C'est là pour que SPICE ne déclare pas d'erreur de circuit ouvert et n'interrompe pas l'analyse.
De plus, le choix des fréquences pour la simulation (60 Hz) est assez arbitraire, car les résistances répondent uniformément pour toutes les fréquences de tension et de courant alternatifs. Il existe d'autres composants (notamment les condensateurs et les inductances) qui ne répondent pas uniformément aux différentes fréquences, mais c'est un autre sujet ! (Figure ci-dessous)
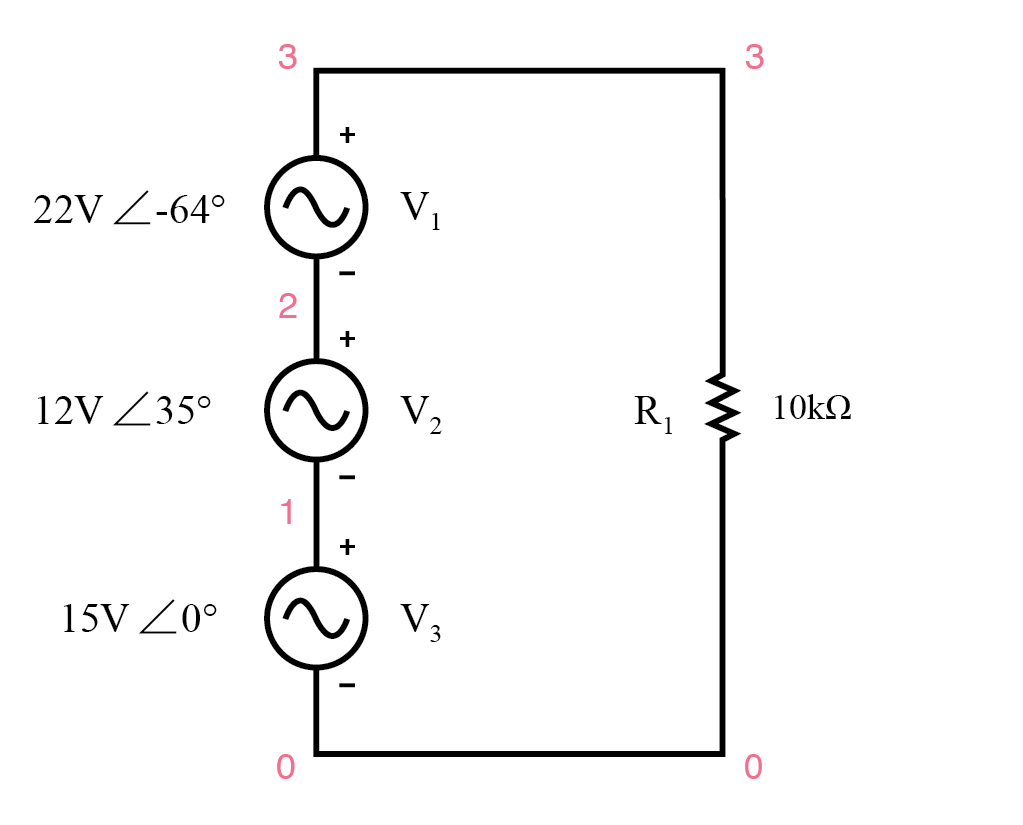
Schéma du circuit d'épices.
Effectivement, nous obtenons une tension totale de 36,81 volts -20,5° (en référence à la source de 15 volts, dont l'angle de phase a été arbitrairement fixé à zéro degré afin d'être la forme d'onde de "référence").
À première vue, c'est contre-intuitif. Comment est-il possible d'obtenir une tension totale d'un peu plus de 36 volts avec des alimentations 15 volts, 12 volts et 22 volts connectées en série ? Avec le courant continu, cela serait impossible, car les chiffres de tension s'ajouteront ou soustrairont directement, selon la polarité.
Mais avec le courant alternatif, notre « polarité » (déphasage) peut varier n'importe où entre l'aide totale et l'opposition totale, ce qui permet une telle sommation paradoxale.
Et si nous prenions le même circuit et inversions l'une des connexions de l'alimentation ? Sa contribution à la tension totale serait alors l'inverse de ce qu'elle était auparavant :(Figure ci-dessous)
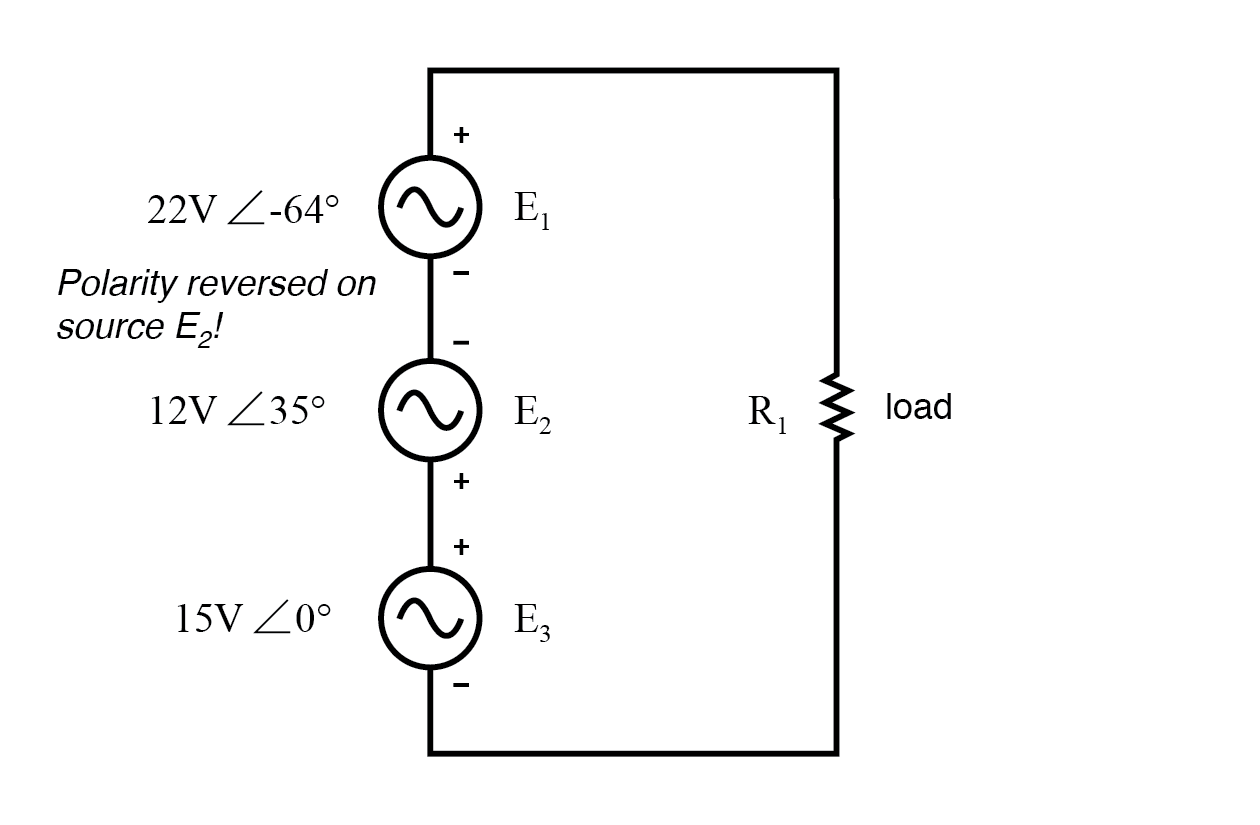
La polarité de E2 (12V) est inversé.
Notez comment l'angle de phase de l'alimentation 12 volts est toujours appelé 35°, même si les fils ont été inversés. N'oubliez pas que l'angle de phase de toute chute de tension est indiqué en référence à sa polarité notée. Même si l'angle est toujours écrit comme 35°, le vecteur sera dessiné à 180° à l'opposé de ce qu'il était auparavant :(Figure ci-dessous)
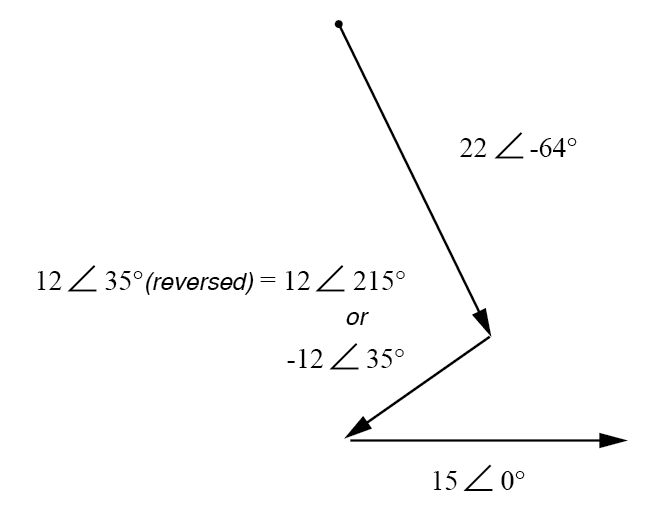
La direction de E2 est inversé.
Le vecteur résultant (somme) doit commencer au point supérieur gauche (origine du vecteur 22 volts) et se terminer à la pointe de la flèche droite du vecteur 15 volts :(Figure ci-dessous)
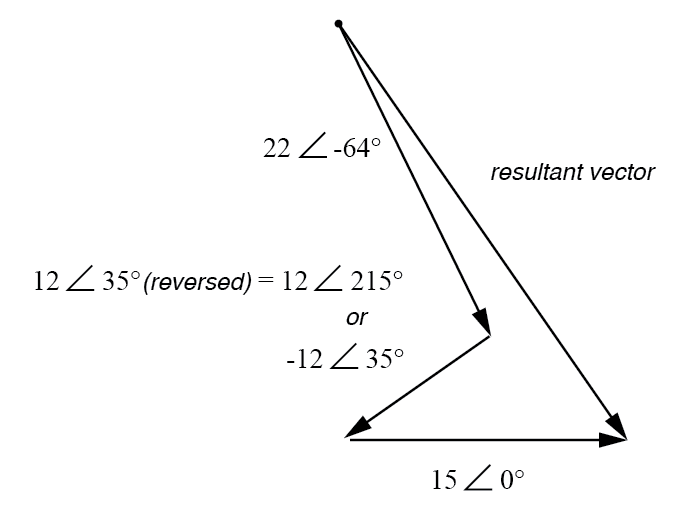
Le résultat est la somme vectorielle des sources de tension.
L'inversion de connexion sur l'alimentation 12 volts peut être représentée de deux manières différentes sous forme polaire :par addition de 180° à son angle vectoriel (ce qui en fait 12 volts 215°), ou une inversion de signe sur la grandeur (ce qui fait - 12 volts ± 35°). Dans tous les cas, la conversion en forme rectangulaire donne le même résultat :
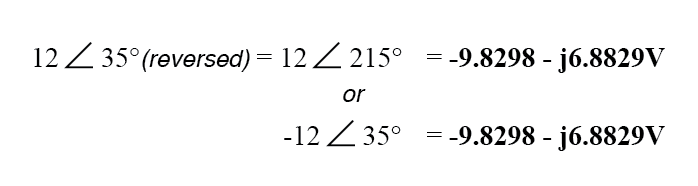
L'addition résultante des tensions sous forme rectangulaire, alors :

Sous forme polaire, cela équivaut à 30,4964 V -60,9368°. Encore une fois, nous utiliserons SPICE pour vérifier les résultats de nos calculs :
AVIS :
- Toutes les lois et règles des circuits CC s'appliquent aux circuits CA, à l'exception des calculs de puissance (loi de Joule), tant que toutes les valeurs sont exprimées et manipulées sous une forme complexe, et que toutes les tensions et courants sont à la même fréquence .
- Lors de l'inversion de la direction d'un vecteur (équivalent à l'inversion de la polarité d'une source de tension alternative par rapport à d'autres sources de tension), il peut être exprimé de deux manières différentes :en ajoutant 180° à l'angle, ou en inversant le signe de la grandeur.
- Les mesures du compteur dans un circuit CA correspondent aux magnitudes polaires de valeurs calculées. Les expressions rectangulaires de quantités complexes dans un circuit alternatif n'ont pas d'équivalent empirique direct, bien qu'elles soient pratiques pour effectuer des additions et des soustractions, comme l'exigent les lois de tension et de courant de Kirchhoff.
FICHES DE TRAVAIL CONNEXES :
- Feuille de travail d'analyse du réseau AC
- Feuille de travail sur les lois de Kirchoff
- Feuille de travail sur la loi d'Ohm
Technologie industrielle
- Circuits de différenciation et d'intégration
- Circuits d'alimentation
- Énergie dans les circuits électriques
- Circuits d'inductance CA
- Circuits de condensateur AC
- Python String count() avec des EXEMPLES
- Fonction Python round() avec EXEMPLES
- Fonction Python map() avec EXEMPLES
- Python Timeit() avec des exemples



