Le théorème de Millman revisité

Vous vous êtes peut-être demandé d'où provenait cette étrange équation pour la détermination de la "tension de Millman" sur les branches parallèles d'un circuit où chaque branche contient une résistance en série et une source de tension :

Certaines parties de cette équation semblent familières aux équations que nous avons vues auparavant. Par exemple, le dénominateur de la grande fraction ressemble visiblement au dénominateur de notre équation de résistance parallèle. Et, bien sûr, les termes E/R dans le numérateur de la grande fraction devraient donner des chiffres pour le courant, la loi d'Ohm étant ce qu'elle est (I=E/R).

Maintenant que nous avons couvert les équivalences de source de Thevenin et Norton, nous avons les outils nécessaires pour comprendre l'équation de Millman. En réalité, l'équation de Millman traite chaque branche (avec sa source de tension série et sa résistance) comme un circuit équivalent Thevenin, puis convertit chacune en circuits Norton équivalents.

Circuit équivalent Thévenin

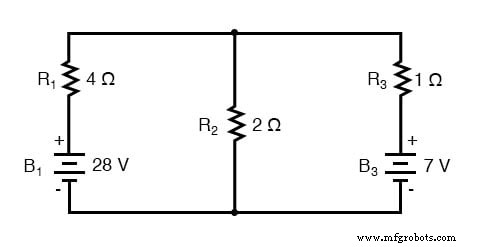
Ainsi, dans le circuit ci-dessus, la batterie B1 et la résistance R1 sont vues comme une source Thevenin à convertir en une source Norton de 7 ampères (28 volts/4 ) en parallèle avec une résistance de 4 . La branche la plus à droite sera convertie en une source de courant de 7 ampères (7 volts / 1 ) et une résistance de 1 en parallèle. La branche centrale, ne contenant aucune source de tension, sera convertie en une source Norton de 0 ampères en parallèle avec une résistance de 2 Ω :

Circuit équivalent Norton

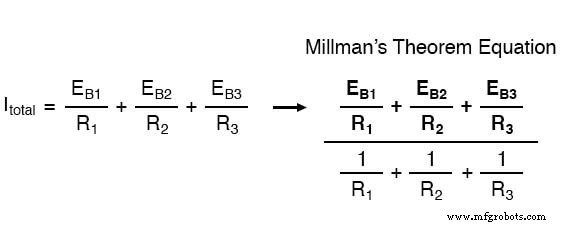
Étant donné que les sources de courant ajoutent directement leurs courants respectifs en parallèle, le courant total du circuit sera de 7 + 0 + 7 ou 14 ampères. Cet ajout de courants de source Norton est ce qui est représenté dans le numérateur de l'équation de Millman :

Équation de Millman

Toutes les résistances Norton sont également en parallèle dans le circuit équivalent, elles diminuent donc pour créer une résistance totale. Cette diminution des résistances de source est ce qui est représenté dans le dénominateur de l'équation de Millman :

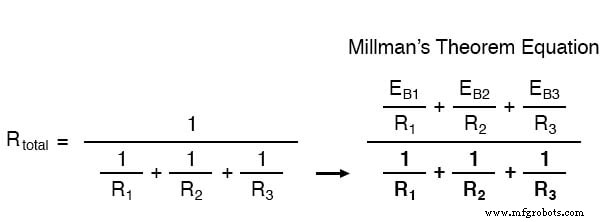
Dans ce cas, la résistance totale sera égale à 571,43 milliohms (571,43 mΩ). Nous pouvons maintenant redessiner notre circuit équivalent en un seul avec une seule source de courant Norton et une résistance Norton :

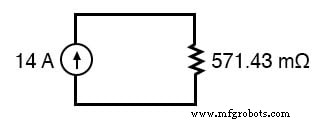
La loi d'Ohm peut maintenant nous indiquer la tension entre ces deux composants (E=IR) :

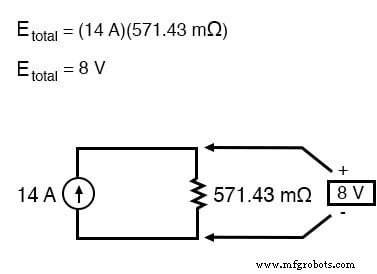
Résumons ce que nous savons sur le circuit jusqu'à présent. Nous savons que le courant total dans ce circuit est donné par la somme de toutes les tensions de dérivation divisée par leurs résistances respectives. On sait aussi que la résistance totale se trouve en prenant la réciproque de toutes les résistances de branche réciproques. De plus, nous devons être bien conscients du fait que la tension totale sur toutes les branches peut être trouvée en multipliant le courant total par la résistance totale (E =IR). Tout ce que nous avons à faire est de rassembler les deux équations que nous avions précédemment pour le courant total du circuit et la résistance totale, en les multipliant pour trouver la tension totale :

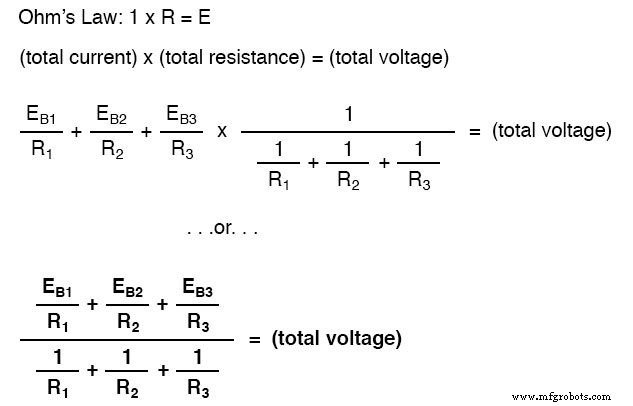
L'équation de Millman n'est rien de plus qu'une conversion de Thevenin à Norton associée à la formule de résistance parallèle pour trouver la tension totale sur toutes les branches du circuit. Alors, espérons-le, une partie du mystère a disparu maintenant !

FICHE DE TRAVAIL CONNEXE :

• Fiche de travail sur le théorème de Millman