Cartes Karnaugh plus grandes à 5 et 6 variables

Les cartes de Karnaugh plus grandes réduisent les conceptions logiques plus grandes. Quelle est la taille suffisante ? Cela dépend du nombre d'entrées, fan-ins , au circuit logique considéré. L'une des grandes sociétés de logique programmable a une réponse.

Les propres données d'Altera, extraites de sa bibliothèque de conceptions client, soutiennent la valeur de l'hétérogénéité. En examinant les cônes logiques, en les mappant sur des nœuds basés sur LUT et en les triant par le nombre d'entrées qui seraient les meilleures à chaque nœud, Altera a constaté que la distribution des ventilateurs était presque plate entre deux et six entrées, avec un joli pic à cinq heures.

La réponse n'est pas plus de six entrées pour la plupart des conceptions et cinq entrées pour la conception logique moyenne. La carte à cinq variables de Karnaugh suit.

K-map à cinq variables

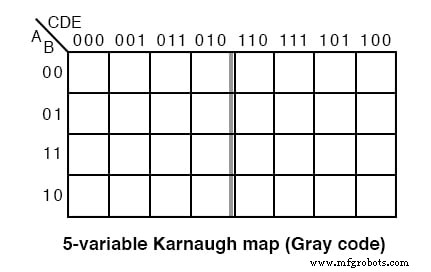
L'ancienne version de la K-map à cinq variables, une carte Gray Code ou une carte de réflexion, est illustrée ci-dessus. Le haut (et le côté pour une carte à 6 variables) de la carte est numéroté en code Gray complet. Le code Gray reflète environ le milieu du code. Cette carte de style se retrouve dans des textes plus anciens. Le nouveau style préféré est ci-dessous.

Version Overlay de la K-map

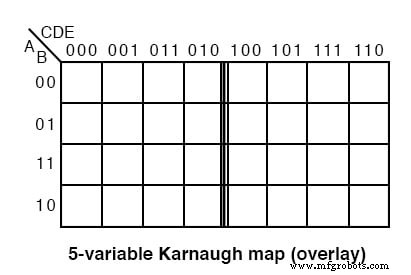
La version superposée de la carte de Karnaugh, illustrée ci-dessus, est simplement constituée de deux cartes identiques (quatre pour une carte à 6 variables), à l'exception du bit le plus significatif de l'adresse à 3 bits en haut.

Si nous regardons en haut de la carte, nous verrons que la numérotation est différente de la carte précédente en code Gray. Si l'on ignore le chiffre le plus significatif des nombres à 3 chiffres, la séquence 00, 01, 11, 10 est à l'en-tête des deux sous-cartes de la carte superposée. La séquence de huit numéros à 3 chiffres n'est pas un code Gray. Bien que la séquence de quatre des deux bits les moins significatifs soit.

Utilisons notre carte de Karnaugh à 5 variables. Concevez un circuit qui a une entrée binaire de 5 bits (A, B, C, D, E), avec A étant le MSB (Most Significative Bit). Il doit produire une logique de sortie High pour tout nombre premier détecté dans les données d'entrée.

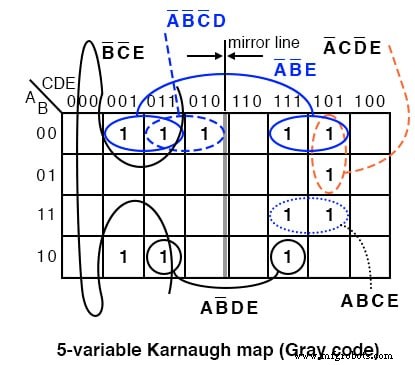
Nous montrons la solution ci-dessus sur l'ancienne carte de code Gray (réflexion) à titre de référence. Les nombres premiers sont (1,2,3,5,7,11,13,17,19,23,29,31). Tracer un 1 dans chaque cellule correspondante. Ensuite, procédez au regroupement des cellules. Terminez en écrivant le résultat simplifié.

Notez que le groupe de 4 cellules A'B'E se compose de deux paires de cellules des deux côtés de la ligne miroir. Il en est de même pour le groupe à 2 cellules AB'DE. C'est un groupe de 2 cellules par réflexion autour de la ligne miroir. Lorsque vous utilisez cette version de la K-map, recherchez des images miroir dans l'autre moitié de la carte.

Sortie =A'B'E + B'C'E + A'C'DE + A'CD'E + ABCE + AB'DE + A'B'C'D

Ci-dessous, nous montrons la version la plus courante de la carte à 5 variables, la carte superposée.

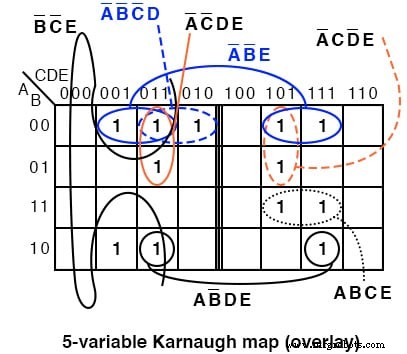
Si nous comparons les modèles dans les deux cartes, certaines des cellules de la moitié droite de la carte sont déplacées car l'adressage en haut de la carte est différent. Nous devons également adopter une approche différente pour repérer les points communs entre les deux moitiés de la carte.

Superposez une moitié de la carte sur l'autre moitié. Tout chevauchement entre la carte du haut et la carte du bas est un groupe potentiel. La figure ci-dessous montre que le groupe AB'DE est composé de deux cellules empilées. Le groupe A'B'E se compose de deux paires de cellules empilées.

Pour les A'B'E groupe de 4 cellules ABCDE =00xx1 pour le groupe. C'est A,B,E sont les mêmes 001 respectivement pour le groupe. Et, CD=xx c'est-à-dire que cela varie, pas de points communs dans CD=xx pour le groupe de 4 cellules. Depuis ABCDE =00xx1 , le groupe de 4 cellules est couvert par A'B'XXE =A'B'E .

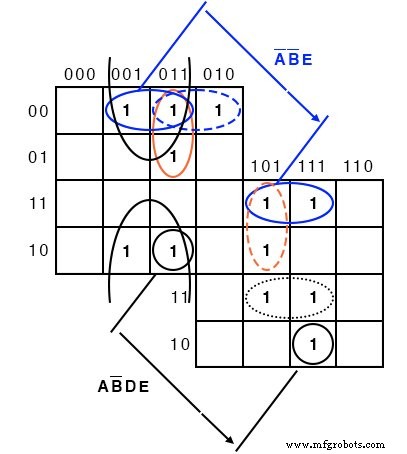
La carte superposée à 5 variables ci-dessus est affichée empilée.

Voici un exemple d'une carte de Karnaugh à six variables. Nous avons empilé mentalement les quatre sous-cartes pour voir le groupe de 4 cellules correspondant à Out =C’F’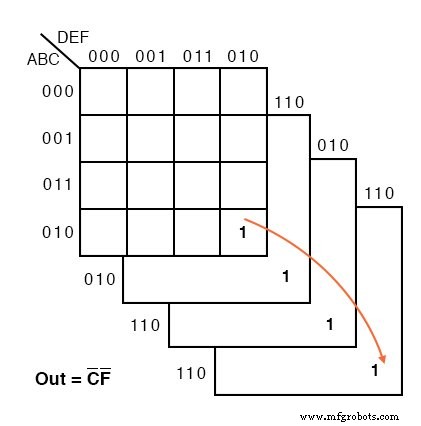

Un comparateur d'amplitude (utilisé pour illustrer une K-map à 6 variables) compare deux nombres binaires, indiquant s'ils sont égaux, supérieurs ou inférieurs l'un à l'autre sur trois sorties respectives. Un comparateur d'amplitude à trois bits a deux entrées A₂ A₁ A₀ et B₂ B₁ B₀ Un comparateur d'amplitude de circuit intégré (7485) aurait en fait quatre entrées, mais la carte de Karnaugh ci-dessous doit être maintenue à une taille raisonnable. Nous ne résoudrons que pour le A>B sortie.

6 K-map variables

Ci-dessous, une carte de Karnaugh à 6 variables facilite la simplification de la logique pour un comparateur d'amplitude à 3 bits. Il s'agit d'un type de carte superposée. Le code d'adresse binaire en haut et en bas à gauche de la carte n'est pas un code Gray complet à 3 bits.

Bien que les codes d'adresse à 2 bits des quatre sous-cartes soient du code Gray. Trouvez des expressions redondantes en empilant les quatre sous-cartes les unes sur les autres (illustrées ci-dessus). Il pourrait y avoir des cellules communes aux quatre cartes, mais pas dans l'exemple ci-dessous. Il a des cellules communes aux paires de sous-cartes.

La sortie A>B ci-dessus est ABC>XYZ sur la carte ci-dessous.

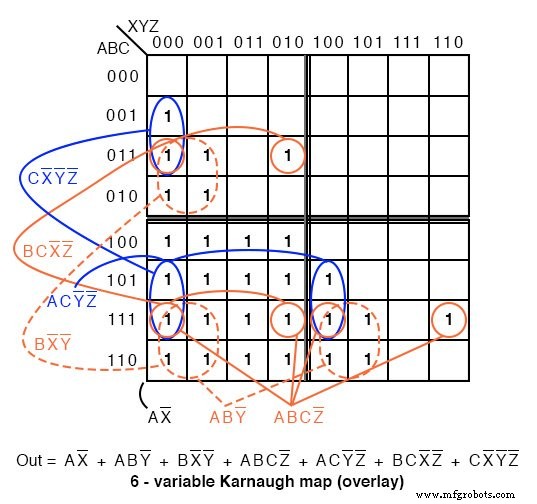
Où que ce soit ABC est supérieur à XYZ , un 1 est tracé. Dans la première ligne ABC=000 ne peut pas être supérieur à l'une des valeurs de XYZ . Non 1 s dans cette ligne. Dans la deuxième ligne, ABC=001 , seule la première cellule ABCXYZ=001000 est ABC supérieur à XYZ . Un seul 1 est inscrit dans la première cellule de la deuxième ligne. La quatrième ligne, ABC=010 , a une paire de 1 s. La troisième ligne, ABC=011 a trois 1 s. Ainsi, la carte est remplie de 1 s dans toutes les cellules où ABC est supérieur à XXZ .

En regroupant les cellules, formez des groupes avec des sous-cartes adjacentes si possible. Tous les groupes de 16 cellules sauf un impliquent des cellules de paires de sous-cartes. Recherchez les groupes suivants :

• 1 groupe de 16 cellules
• 2 groupes de 8 cellules
• 4 groupes de 4 cellules

Le groupe de 16 cellules, AX’ occupe toute la sous-carte en bas à droite ; cependant, nous ne l'entourons pas sur la figure ci-dessus.

Un groupe de 8 cellules est composé d'un groupe de 4 cellules dans la sous-carte supérieure recouvrant un groupe similaire dans la carte inférieure gauche. Le deuxième groupe de 8 cellules est composé d'un groupe similaire de 4 cellules dans la sous-carte de droite recouvrant le même groupe de 4 cellules dans la carte en bas à gauche.

Les quatre groupes de 4 cellules sont indiqués sur la carte de Karnaugh ci-dessus avec les termes de produits associés. Avec les termes de produit pour les deux groupes de 8 cellules et le groupe de 16 cellules, la réduction finale de la somme des produits est affichée, les sept termes.

Compter les 1 s dans la carte, il y a un total de 16+6+6=28 unités. Avant la réduction de la logique K-map, il y aurait eu 28 termes de produit dans notre sortie SOP, chacun avec 6 entrées. La carte de Karnaugh a donné sept termes de produit de quatre entrées ou moins. C'est vraiment la raison d'être des cartes de Karnaugh !

Le schéma de câblage n'est pas représenté. Cependant, voici la liste des pièces du comparateur de magnitude 3 bits pour ABC>XYZ utilisant 4 pièces de la famille logique TTL :

• 1 porte 7410 triple NAND à 3 entrées AX', ABY', BX'Y'
• 2 ea 7420 double porte NAND à 4 entrées ABCZ', ACY'Z', BCX'Z', CX'Y'Z'
• 1 porte NAND à 8 entrées 7430 pour la sortie de termes 7-P

AVIS :

• L'algèbre booléenne, les cartes de Karnaugh et la CAO (conception assistée par ordinateur) sont des méthodes de simplification logique. L'objectif de la simplification logique est une solution à coût minimal.
• Une solution à coût minimal est une réduction logique valide avec le nombre minimal de portes avec le nombre minimal d'entrées.
• Les diagrammes de Venn nous permettent de visualiser des expressions booléennes, facilitant la transition vers les cartes de Karnaugh.
• Les cellules de la carte de Karnaugh sont organisées dans l'ordre du code Gray afin que nous puissions visualiser la redondance dans les expressions booléennes, ce qui entraîne une simplification.
• Les expressions Sum-Of-Products (Sum of Minters) les plus courantes sont implémentées en tant que portes ET (produits) alimentant une seule porte OU (somme).
• Les expressions Sum-Of-Products (logique AND-OR) sont équivalentes à une implémentation NAND-NAND. Toutes les portes ET et les portes OU sont remplacées par des portes NAND.
• Moins souvent utilisées, les expressions Product-Of-Sums sont implémentées sous forme de portes OU (sommes) alimentant une seule porte ET (produit). Les expressions Product-Of-Sums sont basées sur le 0 s, maxterms, dans une carte de Karnaugh.