Don't Care Cells in the Karnaugh Map

Jusqu'à présent, nous avons considéré des problèmes de réduction logique où les conditions d'entrée étaient complètement spécifiées. C'est-à-dire qu'une table de vérité à 3 variables ou une carte de Karnaugh avait 2 ⁿ =2 ³ ou 8 entrées, un tableau complet ou une carte.

Il n'est pas toujours nécessaire de remplir la table de vérité complète pour certains problèmes du monde réel. Nous pouvons avoir le choix de ne pas remplir le tableau complet.

Par exemple, lorsqu'il s'agit de nombres BCD (Binary Coded Decimal) codés sur quatre bits, nous pouvons ne pas nous soucier des codes au-dessus de la plage BCD de (0, 1, 2…9). Les codes binaires à 4 bits pour les nombres hexadécimaux (Ah, Bh, Ch, Eh, Fh) ne sont pas des codes BCD valides.

Ainsi, nous n'avons pas à remplir ces codes à la fin d'une table de vérité, ou K-map, si nous ne nous en soucions pas.

Normalement, nous ne nous soucierions pas de remplir ces codes car ces codes (1010, 1011, 1100, 1101, 1110, 1111) n'existeront jamais tant que nous n'aurons affaire qu'à des nombres codés BCD. Ces six codes invalides sont je m'en fous en ce qui nous concerne.

C'est-à-dire que nous ne nous soucions pas de la sortie que notre circuit logique produit car ceux-ci ne s'en soucient pas.

Je m'en fous

Ne s'en soucie pas dans une carte de Karnaugh, ou une table de vérité, peut être soit 1 s ou 0 s, tant que nous ne nous soucions pas de la sortie d'une condition d'entrée que nous ne nous attendons jamais à voir. Nous traçons ces cellules avec un astérisque, *, parmi les normales 1 s et 0 s.

Lors de la formation de groupes de cellules, traitez la cellule indifférente comme un 1 ou un 0 , ou ignorer les s'en fout.

Ceci est utile si cela nous permet de former un groupe plus grand que ce qui serait autrement possible sans les indifférents. Il n'est pas obligatoire de regrouper tout ou partie des indifférents.

Ne les utilisez en groupe que si cela simplifie la logique.

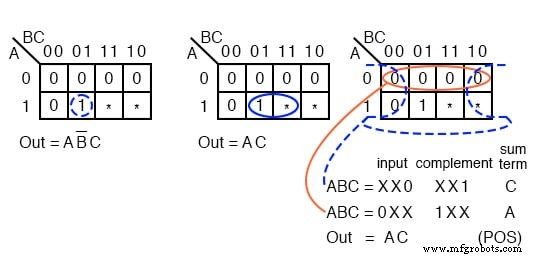
Ci-dessus se trouve un exemple de fonction logique où la sortie souhaitée est 1 pour la saisie ABC =101 sur la plage de 000 à 101 . Nous ne nous soucions pas de la sortie des autres entrées possibles (110, 111) . Cartographiez ces deux-là comme cela ne s'en soucie pas. Nous montrons deux solutions.

La solution à droite Out =AB'C est la solution la plus complexe puisque nous n'avons pas utilisé les cellules indifférentes. La solution du milieu, Out=AC, est moins complexe car nous avons regroupé une cellule indifférente avec le seul 1 pour former un groupe de deux.

La troisième solution, un Product-Of-Sums à droite, résulte du regroupement d'un indifférent avec trois zéros formant un groupe de quatre 0 s. C'est le même, moins complexe, Out=AC .

Nous avons illustré que les cellules indifférentes peuvent être utilisées comme 1 s ou 0 s, selon ce qui est utile.

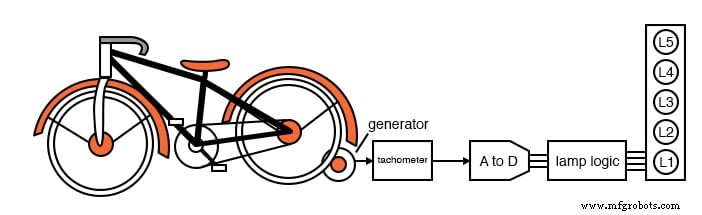
La classe d'électronique du Lightning State College a été invitée à construire la logique de la lampe pour une exposition de vélos stationnaires au musée des sciences local. Lorsqu'un cycliste augmente sa vitesse de pédalage, des lampes s'allument sur un affichage graphique à barres.

Aucune lampe ne s'allumera pour aucun mouvement. Lorsque la vitesse augmente, la lampe inférieure L1 s'allume, puis L1 et L2, puis L1, L2 et L3, jusqu'à ce que toutes les lampes s'allument à la vitesse la plus élevée. Une fois tous les voyants allumés, aucune augmentation supplémentaire de la vitesse n'aura d'effet sur l'affichage.

Un petit générateur de courant continu couplé au pneu de bicyclette produit une tension proportionnelle à la vitesse. Il pilote une carte tachymètre qui limite la tension à l'extrémité supérieure de la vitesse où toutes les lampes s'allument. Aucune augmentation supplémentaire de la vitesse ne peut augmenter la tension au-delà de ce niveau.

Ceci est crucial car le convertisseur A vers D (analogique vers numérique) en aval émet un code à 3 bits, ABC , 2 ³ ou 8 codes, mais nous n'avons que cinq lampes. Un est le bit le plus significatif, C le bit le moins significatif.

La logique de la lampe doit répondre aux six codes de A à D. Pour ABC=000 , pas de mouvement, pas de lampes allumées. Pour les cinq codes (001 à 101) les lampes L1, L1&L2, L1&L2&L3, jusqu'à toutes les lampes s'allumeront, à mesure que la vitesse, la tension et le code A à D (ABC) augmentent.

Nous ne nous soucions pas de la réponse aux codes d'entrée (110, 111) car ces codes ne sortiront jamais de A à D en raison de la limitation dans le bloc tachymètre. Nous devons concevoir cinq circuits logiques pour piloter les cinq lampes.

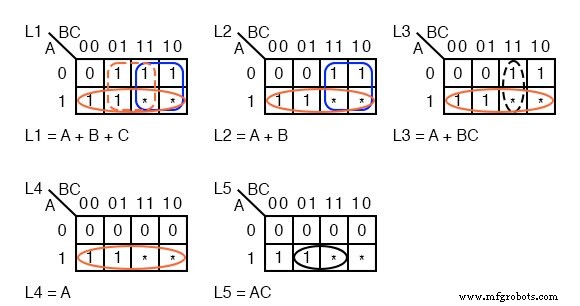
Depuis, aucune des lampes ne s'allume pour ABC=000 de A à D, entrez un 0 dans toutes les K-maps pour la cellule ABC=000 . Puisque nous ne nous soucions pas des codes à ne jamais rencontrer (110, 111) , saisissez des astérisques dans ces deux cellules des cinq K-maps.

La lampe L5 ne s'allumera que pour le code ABC=101 . Saisissez un 1 dans cette cellule et cinq 0 s dans les cellules vides restantes de L5 K-map.

L4 s'allumera initialement pour le code ABC=100 , et restera allumé pour tout code supérieur, ABC=101 , car toutes les lampes en dessous de L5 s'allumeront lorsque L5 s'allumera. Saisissez 1 s dans les cellules 100 et 101 de la carte L4 afin qu'elle s'allume pour ces codes. Quatre 0 's remplissent les cellules L4 restantes

L3 s'allumera initialement pour le code ABC=011 . Il s'allumera également chaque fois que L5 et L4 s'allumeront. Saisissez trois 1 s dans les cellules 011, 100, 101 pour la carte L3. Remplissez trois 0 s dans les cellules L3 restantes.

Lumières L2 pour ABC=010 et des codes plus grands. Remplissez 1 s dans les cellules 010, 011, 100, 101 , et deux 0 s dans les cellules restantes.

Le seul moment où L1 n'est pas allumé est pour l'absence de mouvement. Il y a déjà un 0 dans la cellule ABC=000 . Les cinq autres cellules reçoivent 1 s.

Regroupez les 1 comme indiqué ci-dessus, l'utilisation s'en fout chaque fois qu'un groupe plus important en résulte. La carte L1 montre trois termes de produit, correspondant à trois groupes de 4 cellules.

Nous avons utilisé à la fois des indifférents dans deux des groupes et un indifférent au troisième groupe. Les indifférents nous ont permis de former des groupes de quatre.

De la même manière, les cartes L2 et L4 produisent toutes deux des groupes de 4 cellules à l'aide des cellules indifférentes. La réduction L4 est frappante en ce que la lampe L4 est contrôlée par le bit le plus significatif du convertisseur A vers D, L5=A .

Aucune porte logique n'est requise pour la lampe L4. Dans les cartes L3 et L5, les cellules individuelles forment des groupes de deux avec des cellules indifférentes. Dans les cinq cartes, l'équation booléenne réduite est moins complexe que sans s'en moquer.

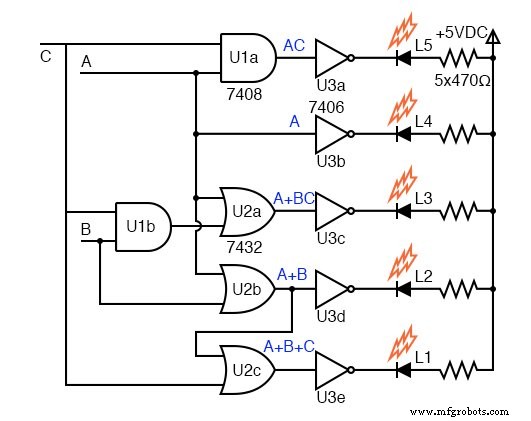
Le schéma de la porte du circuit est ci-dessus. Les sorties des cinq équations K-map pilotent les onduleurs. Notez que le L1 OU gate n'est pas une porte à 3 entrées mais une porte à 2 entrées ayant des entrées (A+B), C , sortie A+B+C Le collectionneur ouvert onduleurs, 7406 , sont souhaitables pour piloter les LED, cependant, ne font pas partie de la conception logique K-map.

La sortie d'une porte de collecteur ouvert ou d'un onduleur est en circuit ouvert au niveau du collecteur interne au boîtier de circuit intégré de sorte que tout le courant du collecteur puisse circuler à travers une charge externe. Un haut actif dans l'un des onduleurs tire la sortie bas, tirant du courant à travers la LED et la résistance de limitation de courant.

Les LED feraient probablement partie d'un relais à semi-conducteurs pilotant des lampes 120 Vca pour une exposition de musée, non illustré ici.

FICHES DE TRAVAIL CONNEXES :

• Fiche de travail des circuits d'affichage numérique
• Feuille de travail de cartographie de Karnaugh