Introduction aux fonctions logiques combinatoires

Le terme « combinatoire » nous vient des mathématiques. En mathématiques, une combinaison est un ensemble non ordonné, ce qui est une façon formelle de dire que personne ne se soucie de l'ordre dans lequel les éléments sont entrés. La plupart des jeux fonctionnent de cette façon, si vous lancez les dés un à la fois et obtenez un 2 suivi d'un 3, c'est la même chose que si vous aviez obtenu un 3 suivi d'un 2. Avec la logique combinatoire, le circuit produit la même sortie quel que soit l'ordre dans lequel les entrées sont modifiées.

Il existe des circuits qui dépendent du moment où les entrées changent, ces circuits sont appelés logique séquentielle. Même si vous ne trouverez pas le terme « logique séquentielle » dans les titres des chapitres, les prochains chapitres traiteront de la logique séquentielle.

Les circuits pratiques auront un mélange de logique combinatoire et séquentielle, la logique séquentielle garantissant que tout se passe dans l'ordre et la logique combinatoire exécutant des fonctions telles que l'arithmétique, la logique ou la conversion.

Vous avez déjà utilisé des circuits combinatoires. Chaque porte logique discutée précédemment est une fonction logique combinatoire. Suivons le fonctionnement de deux portes NAND si nous leur fournissons des entrées dans des ordres différents.

Nous commençons avec les deux entrées à 0.

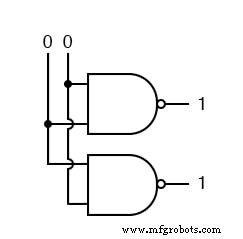
Nous avons ensuite défini une entrée au niveau haut.

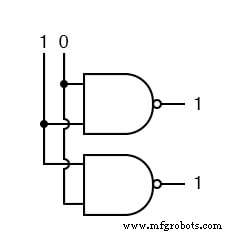
Nous mettons ensuite l'autre entrée au niveau haut.

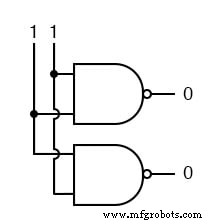
Ainsi, les portes NAND ne se soucient pas de l'ordre des entrées, et vous trouverez le même comportement pour toutes les autres portes couvertes jusqu'à ce point (AND, XOR, OR, NOR, XNOR et NOT).

FICHE DE TRAVAIL CONNEXE :

• Feuille de travail d'algèbre booléenne