Effet des défauts souterrains induits par l'usinage sur l'évolution des dislocations et les propriétés mécaniques des matériaux via la nano-indentation

Contexte

La fabrication ultra-précise à l'échelle nanométrique est largement considérée comme une méthode efficace pour obtenir des nano-composants avec une précision dimensionnelle submicronique et une qualité de surface nanométrique [1]. Certains défauts de sous-surface stables sont laissés à l'intérieur de la pièce après fabrication [2,3,4,5]. Les défauts souterrains affectent non seulement la précision du traitement et la qualité de surface, mais affectent également de manière critique les propriétés mécaniques et la durée de vie des nano-composants. De nombreuses études sur les défauts souterrains ont été menées par la méthode de dynamique moléculaire (MD), en se concentrant principalement sur la formation et l'évolution du défaut souterrain s[6, 7], l'épaisseur de la couche de défauts souterrains (SSD) [8, 9], et l'influence des défauts du sous-sol sur l'intégrité de la surface [10, 11]. Cependant, l'effet des défauts du sous-sol sur les propriétés mécaniques des matériaux des pièces est moins étudié. Les propriétés mécaniques des nanostructures sont essentielles à leurs performances et à leur durée de vie. Par conséquent, l'effet des défauts du sous-sol sur les propriétés mécaniques des matériaux est devenu le problème clé à étudier.

De nombreuses recherches ont été menées pour délibérer de la couche SSD par simulation de dynamique moléculaire du processus de nano-coupe. Narayanan [12] a étudié la formation de failles d'empilement tétraédriques (SFT) dans l'or monocristallin et a introduit le mécanisme induit par déformation de SFT. Inamura [13] a exploré la formation de copeaux et la déformation par glissement de matériau pendant le processus de nano-coupe et a souligné que la formation de copeaux est principalement induite par la déformation par glissement de cisaillement. Pei [14] a étudié l'effet des paramètres de coupe sur l'évolution de la dislocation et la coupe forcée pendant le processus de nano-coupe et a constaté que lorsque la pièce est supérieure à 40  nm, l'effet de taille n'est pas significatif. Dai [15] et Liu [16] ont adopté respectivement des méthodes de simulation et d'expérimentation MD pour étudier l'influence de la structure de l'outil diamanté et de l'effet de la taille sur l'évolution des défauts sous la surface de la pièce. Les études précédentes montrent qu'il existe des défauts de subsurface stables dans la pièce après nano-découpe. Les paramètres de coupe et les paramètres de géométrie de l'outil ont une grande influence sur l'épaisseur et l'évolution de la couche endommagée sous la surface, et même sur la précision du traitement. Cependant, les propriétés mécaniques des matériaux des pièces ne peuvent pas être calculées en analysant les données pertinentes obtenues par nano-coupe.

La nano-indentation est une technique efficace pour caractériser les propriétés mécaniques telles que la dureté et le module d'élasticité [17]. De nombreuses études sur la nano-indentation ont été menées pour évaluer les performances des propriétés mécaniques par des modèles expérimentaux et théoriques. Zimmerman [18] a analysé l'émission de dislocation dans le processus de nano-indentation par le vecteur de glissement. Ruestes [19] a étudié la nano-indentation du Fe monocristallin par simulation MD et a découvert que la génération de dislocations dans le sous-sol est nécessaire pour éliminer le matériau de la zone d'indentation. Huang [20] a effectué des simulations MD de nano-indentation sur une matrice de diamant monocristallin et a constaté que la déformation du matériau diamanté sous indentation était dominée par la nucléation et la propagation de boucles de dislocation 〈110〉 {111}. Sharma [21] a construit artificiellement un modèle de particules dures dans une matrice de cuivre et a analysé l'influence des particules dures sur l'évolution des défauts de subsurface dans le processus d'usinage. Peng [22] a étudié les mécanismes de renforcement des revêtements de graphène sur substrat Cu par nano-indentation, qui résulte de l'effet d'homogénéisation des contraintes généré par l'interface. À partir de l'analyse ci-dessus, on peut voir que les études précédentes sur l'effet des défauts souterrains sont principalement basées sur des matériaux cristallins parfaits ou des défauts hypothétiques de construction artificielle, ce qui est loin des défauts réels du sous-sol. Par conséquent, il est essentiel de construire le modèle de pièce avec des défauts souterrains réalistes pour analyser l'influence des défauts souterrains sur les propriétés mécaniques de la pièce.

Dans cet article, la méthode de nano-coupe a été adoptée pour obtenir le modèle de pièce avec des défauts souterrains conformes aux caractéristiques pratiques. Sur cette base, une simulation de nano-indentation a été réalisée pour étudier l'effet des défauts du sous-sol sur les propriétés mécaniques du cuivre monocristallin. Tout d'abord, le mécanisme de formation et d'évolution des défauts du sous-sol pendant le processus de nano-découpe sera discuté, et les structures de défauts typiques du sous-sol de la pièce après la nano-découpe seront analysées. Deuxièmement, le mécanisme d'interaction entre les défauts de subsurface induits par l'usinage et la nucléation des dislocations lors de l'indentation sera analysé. Troisièmement, sur la base des données charge-déplacement obtenues par nano-indentation, la dureté et le module d'élasticité de Young d'échantillons de cuivre monocristallin seront calculés. Enfin, quelques nouvelles conclusions seront résumées.

Méthodes

Modèle de simulation

Afin d'étudier l'effet des défauts souterrains sur les propriétés mécaniques des matériaux en nano-usinage, le modèle d'échantillon avec défauts souterrains doit être construit. Dans cette recherche, il est réalisé par simulation MD du processus de nano-coupe. Tout d'abord, le modèle de simulation MD est établi et la simulation du processus de nano-découpe est effectuée. Ensuite, l'échantillon et l'outil de coupe se sont détendus pendant un temps suffisant pendant la simulation MD . Enfin, certains défauts stables sont restés dans le sous-sol de pièce. Le diagramme schématique des modèles de simulation MD tridimensionnels est illustré à la figure 1, dans lequel le modèle de nano-coupe est illustré à la figure 1a et le modèle de nano-indentation avec des défauts souterrains est illustré à la figure 1b. Sur la figure 1, les matériaux de la pièce et de l'échantillon sont en cuivre monocristallin et l'outil et le pénétrateur sont en diamant. L'outil diamanté à lame à arc est utilisé dans le processus de nano-coupe et le rayon du bord de l'outil est de 3  nm. Le pénétrateur est de forme hémisphérique dans le processus de nano-indentation et le diamètre est de 6  nm. La pièce et l'échantillon sont divisés en trois parties, qui sont respectivement la couche de Newton, la couche de température et la couche limite. Afin de réduire l'effet de taille et l'effet limite, la condition limite périodique (PBC) est adoptée à la direction [010] du système de simulation. Pour éviter l'interaction initiale entre l'outil et la pièce, l'outil de coupe est placé à 3 nm en haut à droite de la pièce et le pénétrateur est placé à 6 nm de l'échantillon. Les paramètres de simulation détaillés sont indiqués dans le tableau 1.

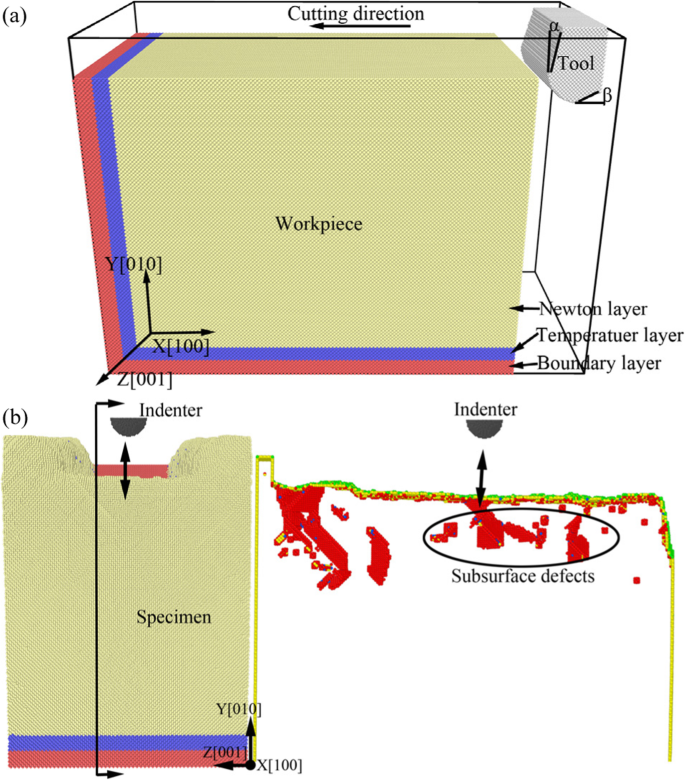
Schéma de principe des modèles de simulation 3-D MD de cuivre monocristallin pour la nano-coupe et la nano-indentation. un Le modèle pour le processus de nano-coupe. b Le modèle pour le processus de nano-indentation avec des défauts souterrains

Fonctions potentielles interatomiques

Dans cette recherche, les simulations MD tridimensionnelles ont été effectuées par un simulateur massivement parallèle atomique/moléculaire à grande échelle (LAMMPS). Le calcul parallèle a été réalisé à l'aide de la bibliothèque d'interfaces de passage de messages. Le potentiel de Morse, le potentiel de la méthode des atomes intégrés (EAM) et le potentiel de Tersoff sont utilisés dans la simulation, qui sont invoqués à partir du progiciel LAMMPS. L'interaction entre les atomes de Cu dans la pièce et les atomes de C dans l'outil est calculée par le potentiel Morse qui est montré dans l'équation. 1 [23].

où r ₀ , α , et D sont respectivement l'espacement atomique, le module d'élasticité et l'énergie de liaison. La valeur est indiquée dans le tableau 2.

La fonction interatomique parmi les atomes de Cu dans la pièce est décrite par le potentiel EAM qui est montré dans les équations. 2, 3 [24, 25].

L'interaction entre les atomes de carbone dans l'outil diamanté est calculée par le potentiel de Tersoff qui est montré dans les équations. 4, 5 [26].

où f _c (r _ij ) est une fonction de troncature entre atomes, V _A (r _ij ) est le potentiel dual du terme d'absorption, V _R (r _ij ) est le double potentiel du terme de répulsion, et r _ij est la distance atomique entre l'atome i et atome j .

Méthodes d'analyse des défauts

Lors de la nano-coupe du cuivre monocristallin, la déformation et les dislocations sont nucléées sous la surface de la pièce. Dans cet article, le paramètre de centro-symétrie (CSP) est introduit pour analyser la nucléation des dislocations et l'évolution des défauts de la pièce. Pour les matériaux cubiques à faces centrées (FCC), la valeur CSP peut être calculée par l'équation. 6 [27].

où R _i est de même longueur les atomes voisins et R _i+6 est la direction opposée des atomes voisins. Les valeurs CSP du cristal FCC, de la dislocation partielle, de la faille d'empilement et des atomes de surface sont respectivement de 0, 2,1, 8,3 et 24,9 [27].

La méthode CSP est capable d'identifier l'échelonnement atomique, mais ne peut pas reconnaître l'état de la structure cristalline atomique locale de la pièce. Par conséquent, l'analyse du voisin commun (CNA) est introduite pour identifier le défaut de structure cristalline locale. Dans la méthode CNA originale, proposée par Honeycutt et Andersen [28], les différentes structures sont représentées par des diagrammes. Actuellement, il existe cinq types de modèles CNA dans OVITO [29], où les structures cristallines locales sont identifiées comme cubique à centre de face (FCC), hexagonale compacte (HCP), cubique centrée (BCC), icosoédrique (ICO), et inconnu, respectivement. Dans cet article, l'algorithme d'extraction de dislocation (DXA) [30] est également introduit pour analyser l'évolution du défaut de dislocation. Par DXA, les différentes structures cristallines de la pièce seront marquées de différentes couleurs et les défauts de dislocation dans la pièce seront représentés par des lignes de différentes couleurs.

Résultats et discussion

Évolution des défauts souterrains dans le processus de nano-coupe

Dans le processus de nano-coupe, sous l'action d'extrusion et de cisaillement de l'outil de coupe sur la pièce, le matériau de surface de la pièce avec l'épaisseur de la profondeur de coupe est supprimé et une nouvelle surface usinée avec une certaine précision de taille et qualité de surface est formée. La déformation élastique-plastique complexe, y compris la déformation sous contrainte et la déformation thermique, se produit dans la surface et la sous-surface de la pièce accompagnant la transformation d'énergie et la concentration de contrainte. Par conséquent, la couche endommagée sous la surface est formée et la puce est retirée. La figure 2 montre les vues instantanées de l'évolution des défauts du sous-sol et de l'enlèvement de matière au cours du processus de nano-coupe du cuivre monocristallin. Sur la figure 2, les atomes sont colorés par la valeur des résultats d'analyse CSP et CNA. Sur les figures 2a et c, les atomes jaunes, verts, rouges et bleus sont des atomes de surface, des atomes de défauts de surface, des atomes de défauts souterrains et des atomes de FCC. On peut voir sur la figure 2 que de nombreuses structures de défauts typiques se forment dans la sous-surface de la pièce au cours du processus de nano-coupe, telles que des défauts ponctuels, des défauts de lacunes, des défauts d'empilement, des défauts de cluster, des dislocations prismatiques et une boucle de dislocation de vis.

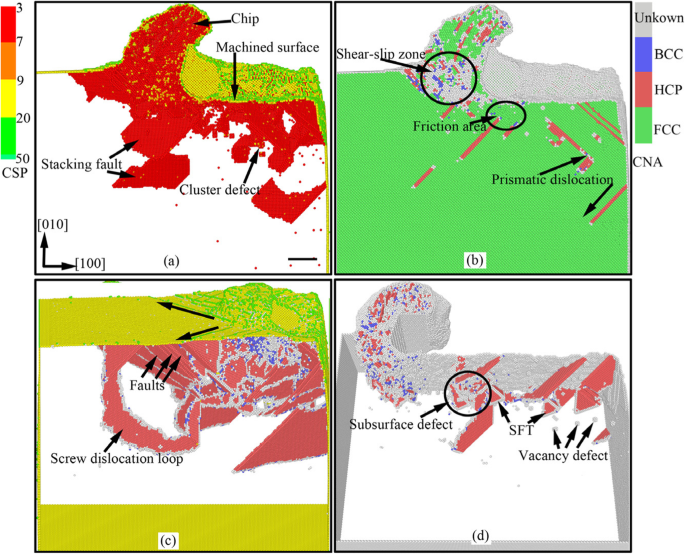
Vues instantanées de l'évolution des défauts du sous-sol pendant le processus de nano-coupe du cuivre monocristallin (Couleur en ligne, barre d'échelle 5 nm). Les distances de coupe de a , b , c , et d sont respectivement 18 nm, 18 nm, 6 nm et 32 nm

En raison de l'effet de compression et de cisaillement de l'outil de coupe, la déformation par glissement de cisaillement est générée pour les atomes devant la face de coupe et la zone de glissement de cisaillement primaire est formée dans la pièce pendant le processus de nano-coupe, comme le montre la figure 2b. Certains de ces atomes glissent le long de la face de coupe et le copeau de coupe se forme comme le montre la figure 2a. Certains se déplacent vers le bas et la surface usinée se forme sous le frottement de compression de la face de flanc de l'outil, comme illustré sur la figure 2b. D'autres se déplacent vers l'intérieur et les défauts du sous-sol se forment, tels que des défauts d'empilement, des défauts d'amas et des dislocations prismatiques, illustrés aux figures 2a et b.

En raison du frottement et de l'extrusion de la surface du flanc de l'outil, l'accumulation d'énergie se produit pour les atomes près de la face du flanc et les atomes sont transformés en atomes à haute énergie. Lorsque l'énergie atomique est dépassée d'un certain niveau, l'énergie portée par les atomes énergétiques sera libérée et la dislocation se formera sous l'entraînement des atomes énergétiques. Par conséquent, de nombreuses dislocations sont formées dans la zone de friction de la face de flanc, illustrée à la figure 2d. Avec la formation de la surface usinée, les dislocations se nucléent, s'étendent et s'annihilent sous la surface. Enfin, les structures de défauts telles que les défauts d'empilement, les SFT et les défauts d'inoccupation sont laissées dans le sous-sol, comme indiqué sur la figure 2d. Les défauts d'empilement sont nucléés au niveau de la zone de glissement sous l'outil de coupe, puis étendus dans la pièce et finalement annihilés à la surface libre de la pièce. Finalement, la ligne de dislocation est formée à la surface de la pièce. Et la ligne de dislocation est prolongée le long de \( \left[\overline{1}0\overline{1}\right] \), \( \left[\overline{1}01\right] \), et [101] directions. La boucle de dislocation de vis, qui est située au bord de la zone de glissement de cisaillement, est constituée de plusieurs failles d'empilement et d'une série de dislocations de vis. La dislocation de la vis se forme sous l'entraînement de l'état de contrainte de compression de la zone de glissement en cisaillement [11].

Dans le processus de nano-coupe, les dislocations sont nucléées et étendues sous l'action de l'outil de coupe. Parallèlement à l'agrégation et à la libération d'énergie, la force de coupe fluctue avec l'augmentation de la distance de coupe, ce qui est illustré sur la figure 3 en trois dimensions. Sur la figure 3, les courbes noire, rouge et bleue sont respectivement la force d'avance (Fx), la force arrière (Fy) et la force tangentielle (Fz). On peut voir à partir de la figure 3 que le processus de coupe est divisé en deux périodes qui sont l'étape de coupe initiale et l'étape de coupe stable. Au cours de la phase de coupe initiale, la force d'avance et la force arrière augmentent rapidement, de manière rectiligne. La valeur maximale de la force d'avance est atteinte à plus de 1100 nN, mais la force arrière vient d'arriver autour de 600 nN. Lorsque la pointe de l'outil coupe complètement la pièce, la surface usinée est formée, illustrée par le premier petit graphique signé comme surface usinée sur la figure 3. Ensuite, le processus de nano-découpe est transféré à une étape de coupe stable. Au stade de coupe stable, les trois forces fluctuent à leurs positions d'équilibre. La force d'avance moyenne est d'environ 1000 nN et la force de retour moyenne n'est que d'environ 500 nN. On peut voir sur la figure 3 que la force d'avance diminue rapidement à la distance de coupe de 20  nm. C'est parce que l'accumulation d'énergie est arrivée à un certain niveau qui est l'énergie de déformation critique du réseau, illustrée par le deuxième petit graphique de la Fig. 3. Pendant ce temps, une grande résistance est exercée sur l'outil de coupe, ce qui entraîne une force de coupe une valeur de pointe. Ensuite, l'énergie est libérée, ce qui entraîne l'émission de dislocation, et la force de coupe est diminuée, comme le montre le troisième petit graphique de la figure 3. Par conséquent, la force de coupe fluctue pendant la phase de coupe stable. La nucléation, l'extension et l'annihilation des dislocations ont conduit à la fluctuation de la force de coupe et ont finalement abouti au défaut souterrain existant dans la pièce.

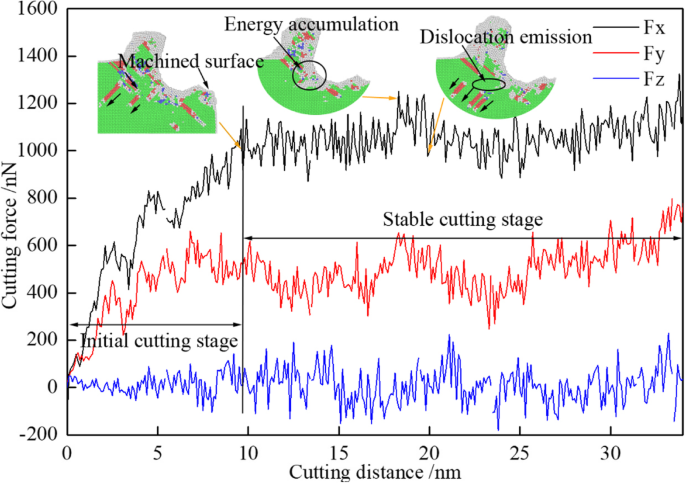
La courbe de variation de la force de coupe avec la distance de coupe (couleur en ligne). Les courbes noire, rouge et bleue sont respectivement la force d'avance (Fx), la force arrière (Fy) et la force tangentielle (Fz)

Afin d'étudier en détail l'évolution et l'émotion des défauts de dislocation dans la sous-surface de la pièce au cours du processus de nano-coupe, la distribution de la dislocation et sa variation avec la distance de coupe sont minutieusement analysées par la méthode CNA. L'évolution des défauts souterrains de la pièce à une certaine zone est illustrée à la figure 4, dans laquelle les distances de coupe des figures 4a, b, c, d, e et f sont respectivement de 8 nm, 10 nm, 12 nm, 20 nm , 24 nm et 32 nm. On peut voir sur la figure 4a que de nombreux défauts de dislocation sont nucléés au niveau de la zone de glissement de cisaillement sous l'action de cisaillement d'extrusion de l'outil de coupe pendant l'étape préliminaire du processus de coupe. En particulier, une dislocation en forme de V et une faille se forment sous l'action motrice de la contrainte et de l'énergie atomiques dans la zone de glissement de cisaillement, illustrée à la figure 4b. Dans le processus de traitement ultérieur, la zone de glissement de cisaillement est déplacée vers l'avant avec l'outil de coupe continue de se déplacer. Du fait de la diminution de l'énergie de déformation, la faille est progressivement annihilée. Pendant que l'outil de coupe continue d'avancer, la zone de friction de la face de flanc est déplacée près du défaut. Et la surface usinée par rugosité est formée sous l'extrusion et le frottement de la face de flanc. Ensuite, le défaut continue de s'annihiler et de se détacher progressivement de la surface de la pièce, comme le montre la figure 4d. Enfin, le défaut est transformé en défaut de cluster qui existe régulièrement dans la sous-surface de la pièce. De même, la dislocation en forme de V formée évolue progressivement en SFT sous l'interaction de deux failles d'empilement et d'un verrou de dislocation. Ces défauts stables sont composés ensemble de la couche déformée sous la surface, comme le montrent les figures 4e et 4f.

Evolution des défauts du sous-sol de la pièce (couleur en ligne). Les distances de coupe de a , b , c , d , e , et f sont respectivement 8 nm, 10 nm, 12 nm, 20 nm, 24 nm et 32 nm

Comme nous le savons, la libération des contraintes résiduelles et la récupération des défauts internes se produiront sur la pièce après traitement de vieillissement. Dans la nano-fabrication réelle, certains des défauts souterrains formés pendant le traitement disparaîtront après le processus d'usinage. Afin de simuler l'état de la pièce après traitement de vieillissement, une relaxation de la dynamique moléculaire est effectuée sur le système de coupe pendant une longue période. Le diagramme de distribution du défaut résiduel dans la sous-surface de la pièce après relaxation MD pendant une longue période est montré sur la figure 5, dans laquelle les atomes sont colorés selon les résultats d'analyse par les méthodes CSP et CNA. On peut voir sur la figure 5 que les dislocations primaires sont annihilées après relaxation. Les défauts d'inoccupation, les défauts d'empilement, le cluster atomique, la dislocation prismatique, la dislocation de la vis, la SFT et la dislocation de la tige d'escalier existent dans la sous-surface de la pièce, comme le montre la figure 5. Selon l'analyse ci-dessus, ces défauts, qui sont formés sous l'induction de contraintes internes complexes et l'interaction des défauts de dislocation affecteront la précision de la taille et la qualité de surface de la pièce après le nano-traitement.

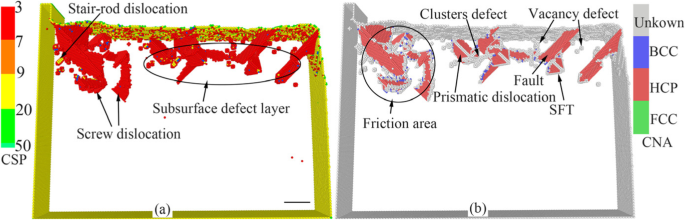
Répartition des défauts résiduels dans la sous-surface de la pièce après découpe nanométrique (couleur en ligne, barre d'échelle 5 nm). un Les atomes jaunes, verts, rouges et bleus sont des atomes de surface, des atomes de défauts de surface, des atomes de défauts souterrains et des atomes FCC. b Les atomes verts, rouges, gris et bleus sont de structure FCC, HCP, inconnue et BCC

Test de nano-indentation sur un échantillon de cuivre présentant des défauts de sous-surface induits par l'usinage

Les défauts résiduels de sous-surface induits par l'usinage régissent les propriétés mécaniques de la surface, en particulier la dureté et le module d'Young. Par conséquent, l'étude de la nucléation et de l'interaction des dislocations lors de la nano-indentation semble fortement nécessaire. Afin d'étudier l'influence des défauts de subsurface induits par l'usinage sur les propriétés mécaniques du cuivre monocristallin, le processus de nano-indentation sur l'échantillon après nano-découpage a été mis en pratique avec les mêmes paramètres que la simulation de nano-découpage. Le résultat de la simulation est montré dans les Fig. 6, 7, 8, 9 et 10. L'image atomique instantanée de la distribution des défauts sous la surface dans l'état initial de nano-indentation est montrée sur la Fig. 6. On peut voir sur la figure qu'il y a plusieurs SFT, un en forme de V dislocation, quelques dislocations prismatiques et quelques défauts d'amas sous le pénétrateur. Ces défauts souterrains peuvent affecter la nucléation de la dislocation et l'expansion de la pièce pendant le processus de nano-indentation. Et puis les propriétés mécaniques du matériau de la pièce sont modifiées.

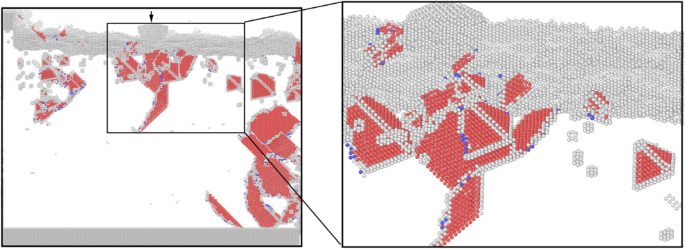
Répartition des défauts sous la surface de la pièce dans l'état d'indentation initial (couleur en ligne). Les atomes rouges, gris et bleus sont de structure HCP, inconnue et BCC

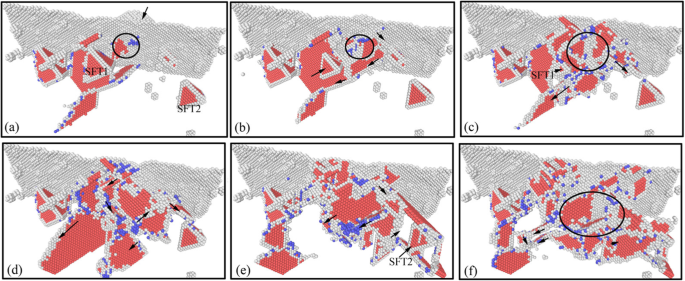
Evolution des défauts de dislocation sous la surface dans le processus de chargement de la nano-indentation (couleur en ligne). Les profondeurs d'indentation correspondantes de a –f sont respectivement 0 nm, 0,5 nm, 1 nm, 2 nm, 3 nm et 4 nm

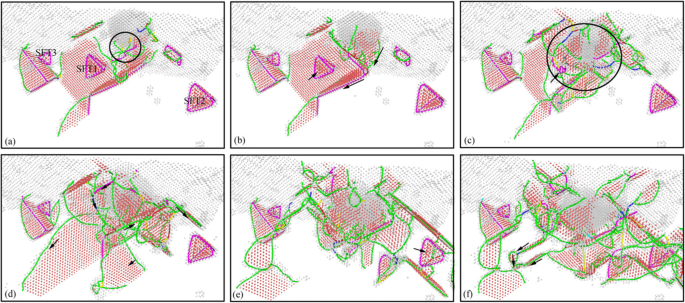
Distribution des dislocations souterraines dans le processus de chargement de la nano-indentation (couleur en ligne). Les profondeurs d'indentation correspondantes de a –f sont respectivement 0 nm, 0,5 nm, 1 nm, 2 nm, 3 nm et 4 nm. Schéma de couleurs :bleu foncé pour les luxations parfaites, vert pour les luxations de Shockley, rose pour les luxations Stair-rod, jaune pour les luxations de Hirth, bleu clair pour les luxations de Frank et rouge pour les luxations non identifiées

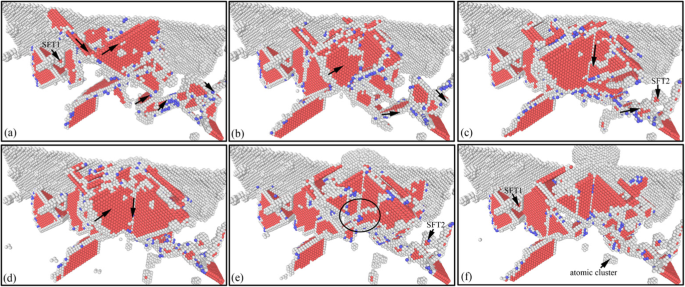
Evolution des défauts du sous-sol dans le processus de déchargement de la nano-indentation (couleur en ligne). Les profondeurs d'indentation correspondantes de a –f sont respectivement 4 nm, 3 nm, 2 nm, 1 nm, 0 nm et − 1 nm

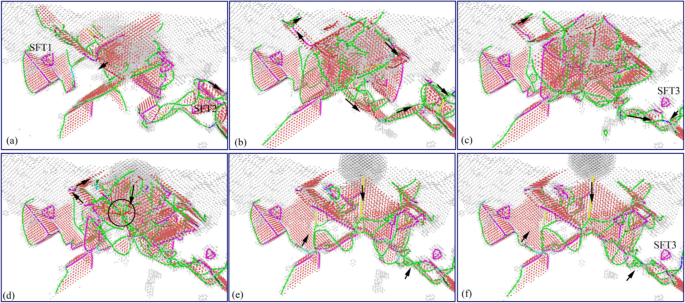
Distribution des dislocations souterraines dans le processus de déchargement de la nano-indentation (couleur en ligne). Les profondeurs d'indentation correspondantes de a –f sont respectivement 4 nm, 3 nm, 2 nm, 1 nm, 0 nm et − 1 nm. Schéma de couleurs :bleu foncé pour les luxations parfaites, vert pour les luxations de Shockley, rose pour les luxations Stair-rod, jaune pour les luxations de Hirth, bleu clair pour les luxations de Frank et rouge pour les luxations non identifiées

L'image de l'évolution atomique des dislocations souterraines au cours du processus de chargement par nano-indentation est illustrée sur la figure 7. On peut voir sur la figure 7a que la nucléation initiale de la dislocation se produit à la surface de l'échantillon lorsque le pénétrateur entre en contact avec la surface du spécimen. Avec la pression vers le bas du pénétrateur, les luxations nucléées s'étendent progressivement. Pendant ce temps, sous l'influence de la contrainte exercée par le pénétrateur, un grand nombre de dislocations ont germé et se sont déplacées le long du système de glissement, comme le montre la figure 7b. Sous l'interaction entre les dislocations nouvellement formées et les défauts de subsurface d'origine, certains défauts simples disparaissent progressivement, et les dislocations en forme de V continuent d'évoluer et de s'annihiler progressivement. Le SFT sous le pénétrateur diminue progressivement, comme le montre la figure 7c. Au fur et à mesure que le processus d'indentation avance, l'échelle des nouveaux défauts de luxation nucléée augmente, et la luxation en forme de V et SFT1 sous indenteur disparaissent progressivement. Simultanément, les défauts de dislocation formés pendant l'indentation évoluent progressivement en boucle de dislocation prismatique, dans laquelle les défauts d'empilement disparaissent progressivement, comme le montre la figure 7d. La boucle de dislocation prismatique nouvellement formée continue de s'étendre jusqu'à SFT2 en bas à droite du pénétrateur. En raison de sa structure stable, le SFT2 ne se déforme pas pendant l'expansion de la boucle de dislocation prismatique, comme le montre la figure 7e. Au fur et à mesure que le pénétrateur appuie vers le bas, la boucle de dislocation prismatique continue de s'étendre vers le bas, et l'échelle des défauts de dislocation dans la zone souterraine augmente progressivement. La structure SFT2 existe de manière stable dans la sous-surface de l'échantillon et n'a aucun changement pendant le mouvement et l'interférence des défauts de dislocation, comme le montre la figure 7 f.

Afin de montrer plus clairement l'évolution et la distribution des défauts du sous-sol pendant le processus d'indentation, la méthode DXA est utilisée pour analyser l'échantillon après indentation. L'image de la distribution des dislocations souterraines à chaque instant correspondant à la Fig. 7 est obtenue par analyse DXA, comme le montre la Fig. 8. Les dislocations sont colorées selon le schéma suivant :bleu foncé pour les dislocations parfaites, vert pour les dislocations de Shockley, rose pour Stair-rod luxations, jaune pour les luxations de Hirth, bleu clair pour les luxations de Frank et rouge pour les luxations non identifiées.

On peut voir sur la figure 8 que la sous-surface de la pièce se compose principalement d'une dislocation de Shockley et d'une dislocation Stair-rod dans l'état d'indentation initial. La SFT qui existait dans le sous-sol est une structure tétraédrique régulière constituée de six dislocations de tiges d'escalier. Lorsque le pénétrateur entre en contact avec la pièce, la nucléation de la dislocation sur la surface de la pièce est une dislocation de Hirsh jaune, comme le montre la figure 8a. Lorsque le pénétrateur s'enfonce, un grand nombre de dislocations sont nucléées et déplacées le long du système de glissement. Les luxations de Hirsh jaunes sont progressivement remplacées par des luxations de Shockley vertes, comme le montre la figure 8b. Sous l'interaction entre les dislocations nouvellement formées et le SFT1 d'origine, certaines dislocations simples disparaissent progressivement, comme le montre la figure 8c. L'échelle des dislocations souterraines augmente avec la baisse du pénétrateur, et les dislocations nouvellement formées sont principalement des dislocations vertes de Shackley. L'interaction entre les luxations de Shockley et SFT1 entraîne la diminution progressive de la taille de SFT1 et la disparition éventuelle de SFT1, comme le montre la figure 8d. Avec l'augmentation de l'échelle des défauts, le nombre et les types de dislocations dans le sous-sol de l'échantillon augmentent. Il existe des types de dislocations inconnues rouges formées dans la subsurface, et plusieurs dislocations de Shockley constituaient la boucle de dislocation du prisme, comme le montre la figure 8e. Sous l'interaction de la luxation de Shockley et de la luxation Stair-rod, les SFT2 et SFT3 loin de la région d'indentation n'ont finalement pas disparu, en raison de l'extrusion plus faible de l'indenteur, comme le montre la figure 8f.

L'image d'évolution de la dislocation souterraine pendant le processus de déchargement par nano-indentation est montrée sur la figure 9. La figure 10 montre l'image de distribution de la dislocation souterraine correspondant à la figure 9. À partir des deux graphiques, on peut voir que l'échelle des défauts souterrains augmente au début, puis diminue progressivement au cours du processus de déplacement vers le haut du pénétrateur. Elle est causée par la fonction globale entre la libération continue de l'énergie de déformation du matériau et la force d'adhérence exercée par le pénétrateur sur l'échantillon. Au stade initial du processus de déchargement, la force d'adsorption ascendante de l'effet du pénétrateur sur l'échantillon n'est pas significative. L'évolution des défauts souterrains est principalement entraînée par l'énergie de déformation du matériau, ce qui entraîne une augmentation de l'échelle des défauts souterrains. Et les principaux types de luxations dans la scène sont la luxation de Shockley verte et la luxation en échelle rose, comme le montrent les Fig. 9a,b et 10a,b. L'interaction entre la dislocation SFT2 et Shockley à proximité fait que la dislocation rose de la tige d'escalier se transforme en dislocation Shackley verte dans la zone éloignée de l'action du pénétrateur. Pendant ce temps, le SFT2 est transformé en un défaut plus petit qui est SFT3, comme le montrent les Fig. 9c et 10c. Avec le soulèvement continu du pénétrateur, l'effet de liaison et d'adsorption exercé par le pénétrateur sur l'éprouvette augmente progressivement. Accompany with the deformation energy release, the size and types of dislocations in subsurface increase. And more perfect dislocations, Hirh dislocations, and unknown dislocations are formed, as shown in Figs. 9d and 10d. In later stage of unloading process, the material deformation energy is basically released, and the evolution of subsurface defects is dominated by the adsorption from the indenter. Therefore, the subsurface defects are annihilated rapidly, and the scale of subsurface defects decreases rapidly. And a typical Hirsch dislocation is formed in the direction of the indenter upward, which is shown in Figs. 9e, f and 10e, f. Finally, the scale of subsurface defects decreases considerably, and some typical subsurface defects, such as SFT and atomic clusters, are gradually disappeared. From the above analysis, it can be seen that secondary processing (nano-indentation) can restore the typical internal defects formed in nano-cutting, and the subsurface damage becomes more serious in the secondary processing area. These characteristics of subsurface defects will affect the mechanical properties of materials. Hence, it is necessary to study the effect of subsurface defects on the mechanical properties of material.

Mechanical properties of materials can be calculated by load-displacement curve, such as hardness, elastic modulus, and yield strength. In this study, hardness and Young’s modulus of single crystal copper were investigated. The variation of load on the indenter was monitored during the nano-indentation process, and the load-displacement curve of the nano-indentation process was drawn, as shown in Fig. 11. The max indentation depth of the red and black curves respectively is 2 nm and 3 nm, in which both loading and unloading processes are included. The upward direction of load is defined as positive direction, so the load-displacement curves are all above the zero line in the process of loading, while the load on the indenter changes from positive to negative during unloading. The elasticity restore of deformed matrix material exerts an upward force on the indenter. Therefore, in order to keep the indenter raising in uniform speed, a downward force (positive) is required. With the gradual recovery of deformation, the force gradually decreases until it disappears. Then the force applied on the indenter becomes negative, and the absolute value of the force first increases and then decreases. From the graph, it can be seen that the specimen is in the stage of elastic deformation during loading process, and the load increases in proportion to the displacement. When the displacement of the indenter is 1 nm, the load on the indenter is fluctuated dramatically, as indicated by the arrow on the left side of Fig. 11. This is because that the indenter is pressed down to the SFT1 shown in Fig. 7, which results in the greater impediment to the indenter. When the indenter displacement is in the range of 2 to 3 nm, the fluctuation amplitude of the load increases. This is because the indenter is pressed down to the SSD layer, and the impediment of the indenter to the subsurface defect in the specimen is more significant, so the fluctuation amplitude of the load increases significantly.

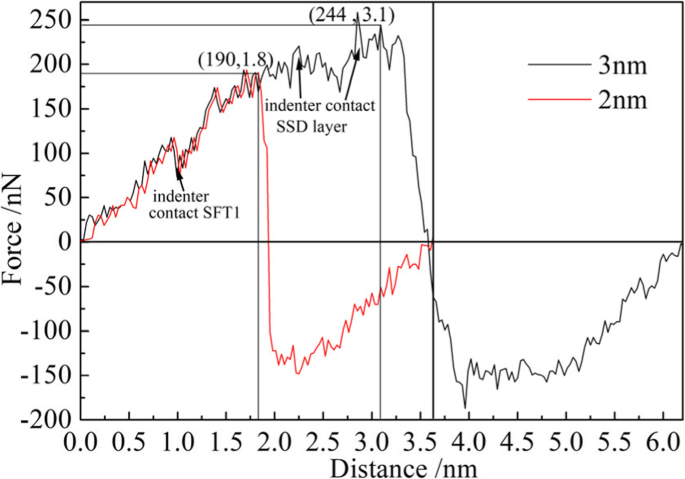
Load-displacement curve of nano-indentation on the machining-induced specimen (color online). The maximum indentation depth of the black curve and the red curve respectively is 3 nm and 2 nm

According to Oliver-Pharr Method [31], nano-indentation hardness can be defined as indentation load divided by the contact area between indenter and specimen, which is calculated by Eq. 7.

In which, F _max is the peak value of the load. Un _c is projected contact area for indenter and specimen, which can be obtained by

où r is contact radius for indenter. Because the indenter is hemispherical in shape, r is approximately equal to indentation depth.

The elastic deformation of single crystal copper material is caused by the load exerted from indenter. Based on the previous load-displacement curve, Young’s modulus (E ) of single crystal copper can be calculated by Eq. 9.

où F is applied load, S is contact area, r is projection radius of indenter, DL is material deformation along loading direction, which is equal to indentation depth, and L is the total length of material along loading direction. In this study, L is equal to 30 nm.

According to the Oliver-Pharr method and load-displacement data, nano-indentation hardness and Young’s elastic modulus of single crystal copper materials with subsurface defects can be calculated based on Eqs. 7, 8, 9. Table 3 shows the applied load acting on the specimens by indenter with different indentation depths.

The nano-indentation hardness of single crystal copper can be calculated by Eqs. 7 and 8 combining the data in Table 3. When the maximum depth is 2 nm, F _max =190.67 nN and from Fig. 11 r =2.75 nm. The calculated value of nano-indentation hardness H2 is 8.029 GPa. When the maximum depth is 3 nm, F _max =244.66 nN and r =3 nm. The calculated value of nano-indentation hardness H3 is 8.675 GPa, which is slightly larger than it obtained at indentation depth of 2 nm. It is because the indenter is pressed down to the subsurface defects area at indentation depth of 3 nm, and the deformation resistance of the subsurface defects increases. Therefore, the hardness of the single crystal copper increased. It can be concluded from the result that the subsurface defects make the machined surface much harder, which is work-hardening phenomenon.

The Young’s modulus E of single crystal copper can be calculated by Eq. 9 combining the data in the Table 3. The calculation results are shown in Table 4. It can be noted that the Young’s modulus becomes distinctly higher when the indentation depth is smaller than 1.5 nm. In the initial stage of nano-indentation, the indenter does not contact the defects residual area in subsurface. However, the work-hardening effect makes the specimen material not easily be occurred elastic deformation; therefore, the Young’s modulus of single crystal copper is larger in the initial stage of indentation. The value of Young’s modulus is 119.4 GPa when indentation depth is 2 nm, which is almost the same with Zhang’s research (120.4 GPa) [14]. With the increase of indentation depth, the Young’s elastic modulus of single crystal copper specimens decreases gradually, and the ability of materials to resist elastic deformation is weakened. It is due to the permanent elastic deformation is derived from the dislocation motion and its interaction with subsurface defects. It has been revealed that the nano-cutting-induced subsurface defects will affect the physical and mechanical properties of single crystal copper materials, which is also applicable to other FCC materials. The existence of subsurface defects will enhance the hardness of machined surface and weaken the ability of material to resist elastic deformation, in which the mutual evolution between dislocations and subsurface defects plays an important role. Therefore, it is very important to predict the thickness of subsurface deformation layer and study the surface properties for nano-fabrication.

Conclusions

The subsurface defects stable exist in workpiece after nano-cutting can affect the mechanical properties, which is critical to the service performance and life of nano-structures. The previous studies are mainly based on perfect crystal materials or artificial constructing hypothetical defects, which is far from the actual subsurface defects. In this paper, molecular dynamics simulation of nano-cutting is performed to construct the specimen model with subsurface defects. Based on the built MD model, nano-indentation simulation is carried out to study the influence of machining-induced subsurface defects on the physical and mechanical properties of single crystal copper materials. The interaction mechanism between dislocation and complex defects during nano-indentation is studied. The nano-indentation hardness and Young’s elastic modulus of single crystal copper materials are calculated. Based on the above analysis, some interesting conclusions can be drawn as follows.

1. 1.

   The dislocation nucleation and expansion in workpiece subsurface are driven by the extrusion and shearing action of cutting tool during the nano-cutting process, which results in the fluctuation of cutting force. After nano-cutting, there are stable defect structure residues in the subsurface of workpiece, such as vacancy defects, stacking faults, atomic clusters, SFT, and stair-rod dislocations, which together constitute the subsurface defect layer of workpiece.

2. 2.

   The existence of subsurface defects affects the nucleation and expansion of dislocations during nano-indentation process. Some stable defects directly below the indenter, such as V-shaped dislocation and SFT1, are annihilated after indentation. And SFT2 far from the indentation region is transformed into a smaller one. Secondary processing of nano-indentation can restore typical internal defects of the workpiece, but the subsurface defects in the secondary processing area are aggravated.

3. 3.

   The nano-indentation hardness of specimens increases with the introduction of subsurface defects, which results in the formation of work-hardening effect. The Young’s modulus of single crystal copper is larger in the initial stage of indentation and gradually decreases with the increase of indentation depth. The existence of subsurface defects can weaken the ability of material to resist elastic deformation, in which the mutual evolution between dislocations and subsurface defects plays an important role.

Disponibilité des données et des matériaux

The conclusions made in this manuscript are based on the data which are all presented and shown in this paper.

Abréviations

MD:

Dynamique moléculaire

SSD:

Subsurface defects

SFT:

Stacking fault tetrahedral

PBC :

Periodic boundary condition

LAMMPS :

Simulateur massivement parallèle atomique/moléculaire à grande échelle

MAE :

Méthode de l'atome embarqué

CSP:

Centro-symmetry parameter

FCC :

Face center cubic

CNA:

Common neighbor analysis

HCP:

Close-packed hexagonal

BCC:

Body centered cubic

ICO:

Icosohedral

DXA:

Dislocation extract algorithm