Dichroïsme circulaire accordable géant de réseaux de nanocroissants métalliques chiraux extrinsèques à grande surface

Introduction

Un objet est chiral si sa structure diffère de son énantiomère miroir [1]. La chiralité est une propriété omniprésente possédée par une grande variété de composés, tels que des substances biologiques et chimiques, ou des métamatériaux artificiels [2]. Cette propriété structurelle est largement utilisée dans de nombreux domaines, tels que la physique, la biologie, la chimie et la médecine [3,4,5,6]. Les nanostructures chirales de métaux nobles ont été largement étudiées au cours des dernières décennies, en raison de leurs propriétés optiques accordables, qui incluent la rotation optique, la transmission asymétrique de la lumière polarisée circulairement et l'extraordinaire dichroïsme circulaire (CD) [7,8,9,10,11 ,12,13,14]. Ces propriétés exceptionnelles sont attribuées à la forte réponse optique de ces structures et elle est générée par des résonances plasmoniques de surface localisées (LSPR). Ce phénomène est sensible à la forme, la taille et l'environnement des nanostructures métalliques [15,16,17]. Pour ces raisons, les nanostructures métalliques chirales peuvent être utilisées dans de nombreuses applications, telles que la réfraction négative [18,19,20], dans la manipulation de la polarisation d'une source lumineuse [21,22,23], et dans la détection de molécules chirales [ 24, 25].

La chiralité optique peut également être générée dans les métamatériaux achiraux en brisant la symétrie du miroir de l'arrangement expérimental via un éclairage oblique. Ce phénomène est connu sous le nom de « chiralité extrinsèque » en raison de l'absence de la double symétrie de rotation du composé. La chiralité extrinsèque a été initialement introduite et prouvée par Bunn en 1945. Zheludev et ses collègues ont découvert la réponse chirale extrinsèque induite par la chiralité extrinsèque dans un anneau métallique fendu. De plus, ils ont étudié le mécanisme d'interaction entre le dipôle électrique et le dipôle magnétique de ces structures [26, 27]. Récemment, Léon et al. [28] ont démontré expérimentalement et théoriquement le grand dichroïsme circulaire dans une métasurface composée de réseaux d'anneaux fendus en métal. Comparées aux nanostructures métalliques chirales, les nanostructures métalliques chirales extrinsèques à grande surface sont plus faciles à fabriquer [29,30,31,32,33,34]. De plus, ils présentent des propriétés optiques chirales encore plus fortes, telles que le CD, ce qui implique que le composé présente des transmissions différentes lorsqu'il interagit avec des ondes incidentes à polarisation circulaire gauche (LCP) ou à polarisation circulaire droite (RCP) [35, 36]. Dans un travail précédent de ce même groupe de recherche, une nanostructure en croissant métallique distribuée de manière aléatoire sur une grande surface a été fabriquée et il a été prouvé qu'elle possède une grande chiralité optique [37]. Cependant, en raison de la faible densité des nanocroissants distribués aléatoirement, le coefficient CD obtenu dans l'expérience était inférieur à celui attendu. De plus, l'uniformité des nanostructures en croissants métalliques répartis aléatoirement présentait plusieurs imperfections qui empêchaient l'utilisation de ce composé dans les applications. Étant donné que la structure matricielle offre une grande densité de cellules et une bonne uniformité. Le développement de méthodes de fabrication simples, bien connues et peu coûteuses pour produire des structures de réseaux métalliques chiraux extrinsèques uniformes et de grande surface constitue un nouveau défi pour promouvoir l'utilisation de la chiralité des métaux dans les applications.

Dans ce travail, un réseau périodique de nanostructures en croissant métallique avec des constantes de réseau comprises entre 500 et 1 000 nm a été fabriqué en utilisant un réseau de microsphères en polystyrène (PS) comme modèle. La valeur maximale du CD (0,51) a été mesurée à 1270 nm pour une constante de réseau de 800 nm. Des simulations de la structure proposée ont été mises en œuvre et se sont avérées être en excellent accord avec les mesures expérimentales. Selon les simulations, le mécanisme principal à la base de cet effet CD intense est l'excitation sélective des LSM via la lumière polarisée circulairement. De plus, l'accordabilité de l'effet CD a été vérifiée expérimentalement en modifiant la constante de réseau de la structure. Étant donné que les microsphères PS sont disponibles dans le commerce, la chiralité extrinsèque du réseau périodique de nanostructures en croissant métallique peut être modulée sur une large gamme spectrale, qui s'étend du visible à l'infrarouge. L'échantillon proposé présente les avantages d'un dichroïsme élevé, d'une fabrication facile et d'une compatibilité avec les techniques de fabrication standard, ce qui pourrait conduire à des applications d'imagerie et de détection de lumière polarisée circulairement.

Méthodes

Les réseaux de réseaux triangulaires équilatéraux de grande surface de nanostructures en croissant métalliques avec différentes constantes de réseau ont été fabriqués en utilisant des nanosphères PS de différentes tailles comme modèles. Les diamètres des nanosphères PS utilisées dans ce travail sont de 500, 650, 800, 850 et 1000 nm. Le processus de fabrication est illustré à la figure 1a. Initialement, un réseau monocouche hexagonal compact de sphères de PS a été formé sur une surface de quartz prétraitée via le processus d'auto-assemblage [38]. La monocouche colloïdale compacte a ensuite été gravée en formant un plasma d'argon pendant 6 min (PDC-32G-2) pour obtenir un modèle non compacté [39, 40]. L'échantillon a été maintenu à une pression de 0,2 mbar et la puissance d'entrée de la lumière a été réglée à 100 mW. Successivement, une couche d'or mince de 50 nm a été déposée par pulvérisation cathodique par faisceau ionique avec un angle d'inclinaison de 45°. Le film d'or a été gravé verticalement par le faisceau d'ions. Enfin, le modèle de nanosphère a été retiré à l'aide d'acétone et les réseaux de réseaux triangulaires équilatéraux de grande surface de nanostructures en croissant métalliques ont été formés. Suite à des considérations géométriques de base, le diamètre du croissant peut être ajusté en choisissant un diamètre différent des nanosphères PS. De plus, l'épaisseur du film est directement accessible en contrôlant la quantité d'or déposée sur l'échantillon, et la largeur maximale du croissant w du métal est donné comme

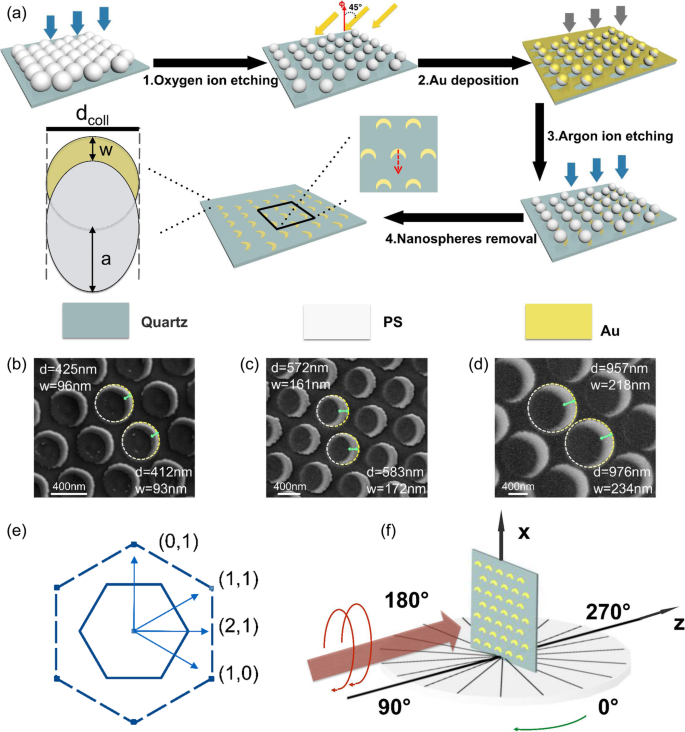
un Croquis du processus de préparation du croissant et de la géométrie des particules indiquant le diamètre d _coll du colloïde de masquage et la largeur maximale du croissant w du métal. La flèche rouge indique la direction positive de l'axe du miroir des nanocroissants ; b –d Images SEM de la structure avec constantes de réseau :b 500 nm, c 800 nm, d 1000 nm. La longueur de la flèche verte représente la largeur maximale de la structure en forme de croissant w . La ligne en pointillé représente le diamètre de la structure en croissant après ajustage avec un cercle (nanosphères PS gravées); e Le réseau réciproque est couvert par les vecteurs de base (1, 0) et (0, 1). Les vecteurs réciproques (1, 1) et (2, 1) sont représentés. Les lignes continues et pointillées dans le diagramme du réseau réciproque représentent les limites des première et deuxième zones de Brillouin, respectivement. f Conception schématique de l'expérience

Substituer Φ =45°, utilisé tout au long des études discutées ici, dans l'équation ci-dessus donne

Il faut noter qu'en réalité, des écarts par rapport à la géométrie idéalisée suggérée sur la figure 1a se produisent. Le w , vu dans les images d'électrons à balayage, Fig. 2b–d, est légèrement plus petit que le cas idéal. En tant qu'incertitudes systématiques supplémentaires, la gravure et l'agrégation des colloïdes doivent être prises en compte. La flèche rouge sur la figure 1a définit la direction positive de l'axe du miroir des nanocroissants qui est vers la direction d'ouverture des nanocroissants. Comme le montre la figure 1b–d, la direction de l'axe du miroir des nanocroissants est cohérente, et cela a pu être déterminé via le processus de dépôt par inclinaison et a été contrôlé artificiellement. Les nanocroissants métalliques s'arrangent régulièrement dans une zone relativement grande. Cependant, l'orientation du réseau est difficile à contrôler en dehors de la zone de mesure optique, qui mesure quelques millimètres carrés, en raison de défauts de fabrication. Par conséquent, l'orientation relative entre la direction des nanocroissants métalliques et le réseau triangulaire équilatéral est aléatoire.

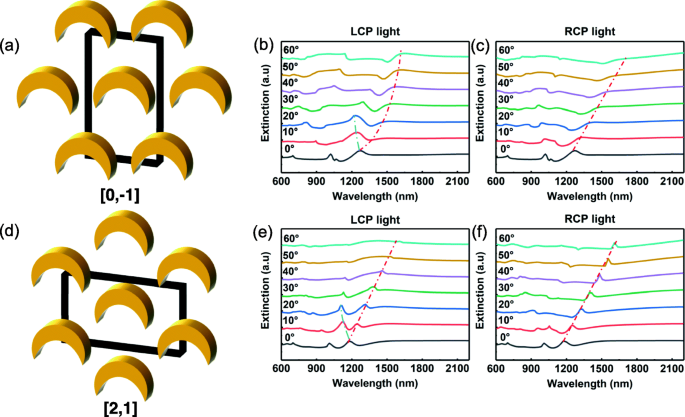
un , d Schéma du réseau où l'axe du miroir des nanocroissants est orienté vers l'axe cristallin [0, − 1] et [2, 1], respectivement (les blocs représentent la cellule cristalline); b , c spectres d'extinction enregistrés en utilisant une lumière incidente avec une polarisation circulaire gauche et droite, respectivement. L'axe du miroir des nanocroissants est dirigé vers la direction [0, − 1] du réseau cristallin; e , f spectres d'extinction enregistrés en utilisant une lumière incidente avec une polarisation circulaire gauche et droite, respectivement. L'axe du miroir des nanocroissants est dirigé vers la direction [2, 1] du réseau cristallin

L'échantillon avec réponse chirale extrinsèque a été modélisé à l'aide d'un solveur d'équation de Maxwell, basé sur la méthode Finite-Difference Time-Domain (FDTD). La structure de réseau de nanocroissants métalliques avec une constante de réseau de 800 nm (c'est-à-dire l'échantillon formé avec des microsphères de PS de 800 nm de diamètre) a été sélectionnée pour effectuer la simulation. Alors que dans l'expérience l'orientation relative entre l'axe du miroir des nanocroissants et le réseau est aléatoire, dans la simulation, l'axe du miroir des nanocroissants a été choisi vers l'axe cristallin [0, − 1] et [2, 1], comme indiqué dans Fig. 2a, d, par souci de simplicité. Ici, le quartz constitue le substrat et l'Au est le métal, comme dans le modèle de Johnson et Christy. Des conditions aux limites périodiques ont été appliquées le long du x - et y -directions. La taille du maillage FDTD a été fixée à 2 nm pour fournir un calcul précis de l'effet plasmonique. En dirigeant la lumière polarisée circulairement à gauche et à droite sur l'échantillon et en faisant simultanément tourner l'échantillon autour de l'axe de symétrie de rotation du nanocroissant métallique, l'angle d'incidence peut être modifié, comme le montre la figure 1e.

Résultats et discussion

Les résonances de surface-réseau (SLR) dans un réseau bidimensionnel de nanoparticules ont été largement étudiées. Les caractéristiques d'extinction dans le spectre résultent des modes de surface du réseau (LSM), qui sont générés par des ordres de diffraction rasante ou des anomalies de Rayleigh (RA) [28, 41]. Dans ce travail, la taille des nanoparticules est approchée par la constante de réseau. Pour cette raison, les caractéristiques d'extinction présentes dans le spectre, qui résultent des LSM, peuvent toujours être observées bien que l'asymétrie de l'indice de réfraction environnemental ait été introduite en ajoutant le substrat de quartz [42]. De plus, un décalage vers le rouge significatif provenant de la condition d'anomalie de Rayleigh, dû au fort couplage du LSPR avec les particules métalliques voisines, peut être observé [43]. Ces phénomènes sont présentés en détail dans les sections suivantes de cet ouvrage.

Lorsque l'axe du miroir des nanocroissants pointe vers l'axe du cristal du réseau [0, − 1] et que l'angle d'incidence de la lumière est de 0°, les spectres d'extinction générés par les deux lumières polarisées circulairement se chevauchent. De plus, chaque spectre présente trois pics d'extinction, situés respectivement à 697 nm, 1019 nm et 1265 nm (Fig. 2b, c). En raison de la faible intensité du pic d'extinction situé à 697 nm et de sa faible contribution à l'effet CD, aucune autre étude sur cette caractéristique n'a été réalisée. Le pic d'extinction situé à 1265 nm est principalement induit par les LSM (± 1, 0), (1, 1) et (− 1, − 1), alors que la caractéristique apparaissant à 1019 nm est majoritairement générée par les LSM (2 , 1) et (− 2, − 1). L'introduction de la structure en croissant supprime la dégénérescence car elle se caractérise par un degré de symétrie relativement faible. En conséquence, le pic d'extinction à 1019 nm se divise lorsqu'il est éclairé par une lumière avec un angle d'incidence de 0°. Lorsque l'angle d'incidence θ augmente et que l'axe du miroir est parallèle à la direction [0, − 1] du réseau cristallin, l'équation de résonance des LSM peut s'écrire comme suit :

\( {\lambda}_{RA}^{\pm}\left(\theta \right)=\frac{\sqrt{3}}{2}\varLambda n\left[1\pm \frac{\sqrt {3}}{2}\sin \left(\theta \right)\right] \) pour les modes (±1, 0), (1, 1) et (−1, −1) ;

\( {\lambda}_{RA}^{\pm}\left(\theta \right)=\frac{1}{2}\varLambda n\left[1\pm \sin \left(\theta \right )\right] \) pour les modes (2, 1), (−2, −1). où Λ est la constante de réseau du réseau triangulaire équilatéral, qui mesure 800 nm ; le symbole ± (positif ou négatif) dépend du premier chiffre des LSM; n est l'indice de réfraction effectif de l'entourage du réseau triangulaire équilatéral, qui prend des valeurs presque identiques (1,25) pour chaque LSM. En introduisant ces valeurs dans les expressions ci-dessus, le pic d'extinction induit par les LSM (± 1, 0), (1, 1) et (− 1, − 1) devrait apparaître à 866 nm, alors que la caractéristique induite par les LSM (2, 1) et (− 2, − 1) à 500 nm. Cependant, les résultats de la simulation montrent que ces pics sont situés à 1265 nm et 1019 nm, ce qui signifie qu'ils sont largement décalés vers le rouge par rapport à ceux calculés. Le décalage vers le rouge est causé par le couplage fort des modes LSPR avec les nanoparticules métalliques voisines [43]. La force de couplage des modes LSPR avec les nanocroissants métalliques voisins est différente pour différentes configurations géométriques et modes, ce qui induit un décalage vers le rouge dans leur réponse optique. Dans ce travail, les différentes valeurs des décalages vers le rouge dépendent de l'indice de réfraction effectif, n , dans l'équation de résonance. L'indice de réfraction effectif mesuré lorsque l'axe du miroir des nanocroissants est vers l'axe du cristal [0, − 1] et θ =0° vaut 1,46 pour les LSM (± 1, 0), (1, 1) et (− 1, − 1), et 2,04 pour les LSM (2, 1) et (− 2, − 1). Au fur et à mesure que l'angle incident augmente, la dégénérescence est supprimée et les pics d'extinction à 1265 nm et 1019 nm s'élargissent ou se divisent. La suppression de la dégénérescence est un processus très compliqué car les efficacités d'excitation des modes LSPR changent avec des tendances différentes lors de l'augmentation de θ . Par conséquent, ce travail se concentre sur le principal facteur qui donne lieu à l'énorme effet CD. Comme le montrent les figures 2b, c, le pic d'extinction situé à 1265 nm est décalé vers le bleu lors de l'augmentation de l'angle d'incidence de la lumière LCP, mais ce phénomène n'est pas observé dans les spectres d'extinction où la lumière RCP est utilisée. Ces résultats montrent une différence significative entre les spectres d'extinction mesurés avec la lumière incidente RCP et LCP et cela peut être lié à l'énorme effet CD mesuré ; alors que la lumière LCP peut exciter les LSM (− 1, 0) et (− 1, − 1), cela ne se produit pas avec la lumière RCP.

Lorsque l'axe du miroir des nanocroissants est aligné avec l'axe [2, 1] du réseau, des résultats similaires sont obtenus. Comme le montre la Fig. 2e, f, lorsque θ =0°, les spectres d'extinction pour les deux types de lumière incidente polarisée circulairement se chevauchent. De plus, chaque spectre présente également trois pics d'extinction, situés respectivement à 697 nm, 1019 nm et 1171 nm. Le pic d'extinction situé à 697 nm n'a pas été pris en considération dans l'analyse suivante. Les observations suggèrent que le pic d'extinction situé à 1171 nm est principalement induit par les LSM (0, ± 1), alors que celui positionné à 1019 nm peut être généré par les LSM (− 1, 1), (1, − 1) , (1, 2) et (− 1, − 2). Lors de l'augmentation de l'angle d'incidence, θ , et lorsque l'axe du miroir est parallèle à la direction [2, 1] du réseau, l'équation de résonance des LSM peut s'écrire comme suit :

\( {\lambda}_{RA}^{\pm}\left(\theta \right)=\frac{\sqrt{3}}{2}\varLambda n\left[1\pm \sin \left( \theta \right)\right] \) pour les modes (0, ±1) ;

\( {\lambda}_{RA}^{\pm}\left(\theta \right)=\frac{1}{2}\varLambda n\left[1\pm \frac{\sqrt{3}} {2}\sin \left(\theta \right)\right] \) pour les modes (−1, 1), (1, −1), (1, 2) et (−1, −2).

Le signe ± (positif ou négatif) dépend du deuxième chiffre des LSM. Quand θ =0°, n est de 1,35 pour les LSM (0, ± 1), alors qu'il mesure 2,04 pour les LSM (− 1, 1), (1, − 1), (1, 2) et (− 1, − 2). Lorsque l'angle incident augmente, les pics d'extinction à 1171 nm et 1019 nm deviennent plus larges ou divisés. De même, lorsque l'axe du miroir des nanocroissants est parallèle à l'axe du cristal [0, − 1], la différence la plus significative entre les spectres d'extinction enregistrés à l'aide de la lumière incidente RCP et LCP est une série de pics d'extinction. Ils sont décalés vers le bleu par rapport au pic situé à 1171 nm. De plus, lors de l'augmentation de l'angle incident, elles n'apparaissent que dans les spectres d'extinction mesurés via la lumière incidente LCP, mais cela ne peut être observé si la lumière RCP est utilisée. Cette observation peut expliquer l'énorme effet CD mesuré puisque seule la lumière LCP peut exciter le (0, − 1) LSM. L'excitation sélective des LSM via une lumière polarisée circulairement à gauche et à droite peut alors être responsable de l'énorme effet CD observé dans les structures de réseaux chiraux extrinsèques et cette observation est cohérente avec la réf. [28].

Une mesure expérimentale a été réalisée pour obtenir les spectres d'extinction et les spectres CD des échantillons. Un système de mesure, qui constitue un spectrophotomètre ultraviolet-visible-proche infrarouge, a été développé. La lumière est dirigée à travers un prisme de Glan-Taylor et une lame quart d'onde à large spectre pour garantir qu'une polarisation circulaire peut être obtenue et que l'échantillon est irradié sous un certain angle. Cet angle peut être contrôlé avec précision en faisant tourner la platine de l'échantillon. Le coefficient CD peut être calculé à l'aide de l'équation suivante :

où L _poste et R _poste sont les intensités d'extinction des nanocroissants métalliques mesurées avec le spectrophotomètre via la lumière LCP et la lumière RCP, respectivement. Les résultats sont présentés sur la figure 3d, e, tandis que les spectres CD sont présentés sur la figure 3f. Pour rapprocher les simulations des conditions expérimentales, les spectres d'extinction des deux configurations ont été superposés (Fig. 3a, b) et les coefficients CD simulés ont été calculés (Fig. 3c). Les simulations sont en bon accord avec les résultats expérimentaux, notamment dans le cas des spectres CD. Comme le montre la figure 3d, e, lorsque θ =0°, les spectres d'extinction mesurés par la lumière incidente LCP et RCP sont quasiment identiques. De plus, deux pics d'extinction importants situés à 696 nm et 1838 nm sont présents. Les résultats suggèrent que le pic d'extinction à 696 nm est généré par le mode LSPR d'ordre élevé. Le pic d'extinction à 1838 nm peut plutôt survenir en raison des LSM (± 1, 0), (1, 1), (− 1,− 1), (0, ± 1) et du mode dipolaire LSPR. À l'augmentation de θ , le pic d'extinction à 696 nm diminue initialement puis augmente à nouveau, bien que son intensité soit différente dans les spectres LCP et RCP. Cette observation est cohérente avec les conclusions des travaux antérieurs de ce groupe de recherche. Le pic d'extinction à 1838 nm ne présente qu'un léger changement et un nouveau pic d'extinction situé à 1390 nm apparaît lors de l'augmentation de θ et lorsque la lumière incidente LCP est utilisée. Cela se traduit par l'excitation des LSM (− 1, 0), (− 1, − 1) et (0, − 1). Lorsque l'échantillon est excité via la lumière incidente RCP, le pic d'extinction à 1838 nm se déplace vers le rouge et son intensité devient plus faible à mesure que θ augmente. Bien qu'il n'y ait pas de pics d'extinction situés à 1390 nm, une nouvelle fonctionnalité apparaît à 1080 nm lorsque θ est augmenté et cela peut être généré par les modes LSPR. Comme le montre la figure 3f, lors d'une augmentation de θ , un pic majeur de CD apparaît et se déplace vers le rouge. Quand θ =30°, la valeur maximale du coefficient CD (0,51) peut être mesurée à 1270 nm. L'excitation sélective des LSM (− 1, 0), (− 1, − 1) et (0, − 1) via la lumière polarisée circulairement déclenche le mécanisme responsable de l'énorme effet CD. En raison des défauts du processus de production, les pics d'extinction et de CD obtenus dans l'expérience sont légèrement plus larges par rapport à ceux simulés.

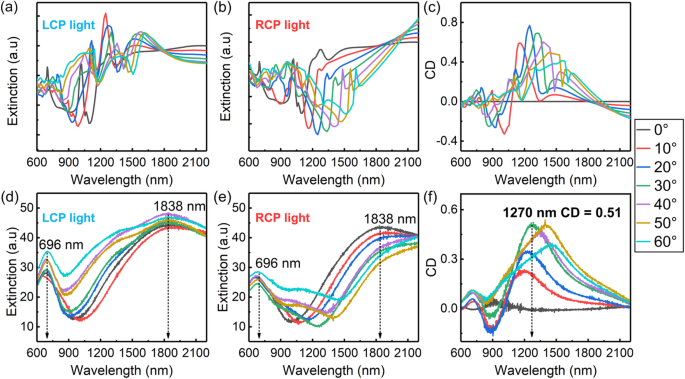
Extinction simulée et mesurée et spectres CD. un –c Spectres d'extinction additifs simulés pour différents angles d'incidence de la lumière polarisée circulairement :a LCP, b RCP et les spectres CD. d –f Spectres d'extinction mesurés pour différents angles d'incidence de la lumière polarisée circulairement :d LCP, e RCP et les spectres CD

De plus, ce travail montre que la chiralité extrinsèque du réseau de nanostructures en croissant métallique peut être ajustée en ajustant le diamètre de la microsphère de PS. La figure 4 montre les spectres CD de plusieurs réseaux de nanocroissants métalliques avec différentes constantes de réseau (c'est-à-dire le diamètre des nanosphères PS) dans la plage de 500 à 1000 nm avec θ =30°. Lors de l'augmentation de la constante de réseau, le pic des spectres CD se déplace vers le rouge de 1019 à 1799 nm, et le coefficient CD reste relativement important (> 0,25). Étant donné que des microsphères de PS avec des diamètres compris entre 50 nm et 10 m sont disponibles dans le commerce, la chiralité extrinsèque de la structure peut être modulée pour son application sur une large gamme de longueurs d'onde allant du visible à l'infrarouge.

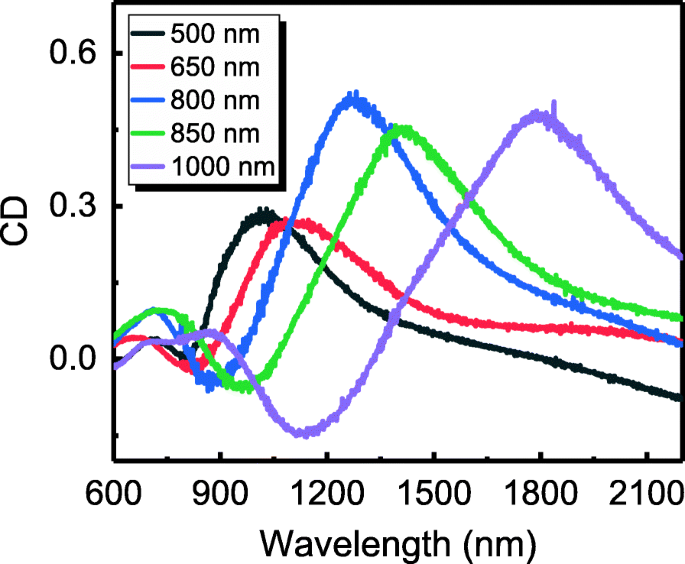
spectres CD de réseaux de nanocroissants métalliques d'un diamètre compris entre 500 et 1 000 nm ; l'angle d'incidence de la source lumineuse est de 30°

Conclusions

En résumé, nous avons démontré que les structures de réseau de nanocroissants métalliques de grande surface présentent un effet chiral extrinsèque considérable, ainsi qu'une modularité élevée et une méthode de fabrication simple. Des échantillons avec différents paramètres de réseau ont été fabriqués avec succès et l'effet CD a été étudié théoriquement et expérimentalement. Le plus grand coefficient CD (> 0,5) a été mesuré à 1270 nm en utilisant un angle d'incidence de 30° dans un réseau de croissants métalliques avec une période de 800 nm. En outre, le spectre CD de telles structures peut être largement réglé, tout en maintenant une grande intensité de pic, en modifiant le diamètre des microsphères de PS. Les emplacements des pics CD varient de 1019 à 1799 nm, lors d'un changement de la constante de réseau dans la plage de 500 à 1000 nm. Les simulations sont en bon accord avec les résultats expérimentaux et l'effet chiral extrinsèque important et accordable des échantillons peut être attribué à l'excitation sélective des LSM induite par LCP et RCP. La structure démontrée pourrait être utile en télédétection et en imagerie de polarisation.

Disponibilité des données et des matériaux

Toutes les données générées ou analysées au cours de cette étude sont incluses dans cet article publié.

Abréviations

LCP :

polarisation circulaire gauche

RCP :

polarisation circulaire droite

CD :

dichroïsme circulaire

LSPR :

résonances plasmoniques de surface localisées

LSMS :

modes de surface en treillis

SLRS :

résonances surface-réseau

SEM :

microscope électronique à balayage