Dynamique de magnétisation modulée par l'interaction Dzyaloshinskii-Moriya dans la jonction tunnel magnétique à couple de transfert de rotation à double interface

Introduction

La mémoire magnétique à accès aléatoire (MRAM) est l'un des candidats les plus prometteurs pour la mémoire non volatile de nouvelle génération grâce à sa faible consommation d'énergie, sa haute densité, sa vitesse d'accès rapide, son endurance presque infinie et sa bonne compatibilité avec la technologie CMOS [1, 2]. Le dispositif élémentaire de la MRAM est la jonction tunnel magnétique (MTJ), qui est composée d'une barrière tunnel prise en sandwich entre deux couches ferromagnétiques (appelées couche pincée et couche libre). Bénéficiant des progrès de l'anisotropie perpendiculaire, la taille des caractéristiques du MTJ a été réduite en dessous de 40 nm voire 1×nm [3,4,5]. Cependant, un défi pour le MTJ inférieur à 40  nm est de maintenir la barrière de stabilité thermique adéquate E = μ ₀ M _s H _k V /2. (avec μ ₀ la perméabilité magnétique sous vide, M _s l'aimantation à saturation, H _k le champ d'anisotropie, V le volume de la couche libre). Comme indiqué par cette équation, E diminue avec la mise à l'échelle de la MTJ, ce qui entraîne une réduction du temps de rétention des données. Pour surmonter ce défi, des MTJ à double interface ont été proposés pour atteindre un E suffisamment élevé au nœud technologique sub-40 nm [6,7,8,9,10]. En utilisant deux couches ferromagnétiques couplées comme couche libre composite, le volume équivalent (V ) dans la double interface MTJ est augmentée afin d'améliorer la barrière de stabilité thermique. Pendant ce temps, la constante d'amortissement est diminuée pour maintenir un faible courant de commutation.

Dans les MTJ à double interface, la structure ferromagnétique/métal lourd (FM/HM) joue un rôle important dans l'optimisation des performances. D'une part, la structure FM/HM augmente le couplage spin-orbite (SOC) pour induire l'anisotropie perpendiculaire. D'autre part, le métal lourd fonctionne comme un espaceur entre deux couches ferromagnétiques de la couche libre composite pour fournir l'interaction Ruderman-Kittel-Kasuya-Yosida (RKKY) [11], qui couple ferromagnétiquement les magnétisations des deux couches ferromagnétiques dans afin qu'ils se comportent comme une couche identique. Par ailleurs, des travaux récents démontrent que le fort SOC du métal lourd combiné aux spins atomiques du ferromagnétique pourrait former un couplage d'échange antisymétrique appelé interaction Dzyaloshinskii-Moriya (DMI) [12, 13]. Par conséquent, le DMI est naturellement induit dans le MTJ à double interface avec des structures FM/HM. Le DMI favorise les textures magnétiques chirales (par exemple, les spirales de spin, les skyrmions et les parois de domaine de type Neel) et affecte considérablement la dynamique de magnétisation, comme validé par les études récentes [14,15,16,17,18,19,20,21 ,22,23,24,25]. Il est important de mentionner que le rôle du DMI deviendra plus compliqué dans le MTJ à double interface, car deux interfaces FM/HM doivent être considérées conjointement avec une interaction RKKY supplémentaire. Par conséquent, il est important de révéler l'effet du DMI sur le MTJ à double interface.

Dans cette lettre, pour la première fois, nous étudions le processus de commutation des MTJ à double interface sous les actions de l'interaction DMI et RKKY. Le MTJ à double interface est commuté par le couple de transfert de spin (STT), qui est une approche courante pour l'écriture de données de la MRAM. Il a été récemment rapporté que le DMI a un effet néfaste sur la commutation STT [21, 22]. Ici, nos résultats démontrent que dans les MTJ à double interface, l'effet néfaste du DMI pourrait être supprimé par l'interaction RKKY, entraînant une commutation rapide et une dynamique plus uniforme. Notre travail prouve la robustesse du STT-MTJ à double interface contre l'effet interfacial négatif.

Méthodes

Le dispositif étudié dans ce travail est illustré sur la figure 1a, avec une structure FM/HM/FM comme couche libre composite. L'épaisseur de la couche HM est ajustée à une valeur appropriée afin que l'interaction RKKY induite couple ferromagnétiquement deux couches FM. L'une des couches FM est magnétiquement plus douce, qui est désignée par FL1 (couche libre 1), tandis que l'autre est magnétiquement plus dure et désignée par FL2 (couche libre 2). Pour commuter l'aimantation de la couche libre composite, un courant est appliqué à la double interface MTJ et génère le STT. Dans ce travail, nous ne considérons que le STT transmis de la couche de référence à FL1, alors que les autres couples entre FL1 et FL2 sont négligés. Ce modèle simplifié est cohérent avec les travaux précédemment rapportés [26,27,28]. Les DMI sont induits dans les interfaces FM/HM et HM/FM et ont des signes opposés en raison de la chiralité différente [29].

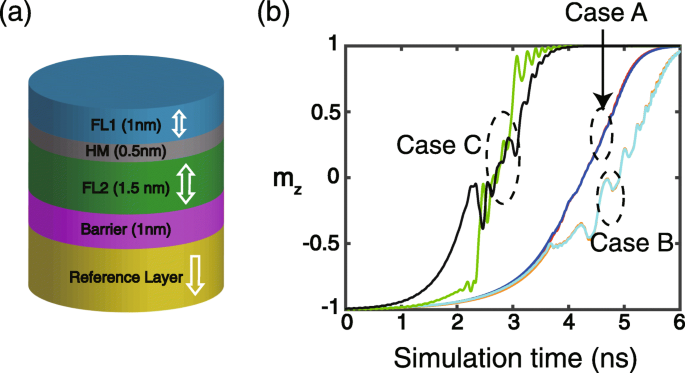
un Structure schématique du dispositif étudié dans ce travail. Les autres couches ne sont pas représentées pour plus de clarté. b Résultats typiques du m dépendant du temps _z (composante perpendiculaire de l'aimantation unitaire). Cas A :σ = 1 × 10 ⁻³ J/m ² , D ₁ =D ₂ = 0 (rouge pour FL1, bleu pour FL2). Cas B :σ = 1 × 10 ⁻³ J/m ² , D ₁ = 1 mJ/m ² , D ₂ =−1 mJ/m ² (orange pour FL1, cyan pour FL2). Cas C :σ = 1 × 10 ⁻⁴ J/m ² , D ₁ =D ₂ = 0 (vert pour FL1, noir pour FL2)

La dynamique d'aimantation des FL1 et FL2 dans le MTJ à double interface est étudiée par simulation micromagnétique. L'évolution temporelle du vecteur d'aimantation unitaire est régie par l'équation de Landau-Lifshitz-Gilbert (LLG) suivante. Nous avons choisi le package OOMMF, un outil de simulation micromagnétique open source [30], pour modéliser la structure du dispositif et résoudre l'équation LLG pour analyser la dynamique de magnétisation.

où γ est le rapport gyromagnétique, m est le vecteur unitaire le long de l'aimantation, z est le vecteur unitaire le long de la direction de l'épaisseur, H _eff est le champ effectif comprenant l'anisotropie perpendiculaire uniaxiale, l'énergie d'échange à 6 voisins, le champ DMI, l'interaction RKKY, le champ de démagnétisation, l'interaction dipolaire et le STT. Les autres paramètres et leurs valeurs par défaut sont répertoriés dans le tableau 1, sauf indication contraire. Ces valeurs de paramètres sont conformes aux technologies de pointe. En ce qui concerne la magnitude DMI, nous considérons une couche libre composite CoFeB/W/CoFeB dans le MTJ à double interface [10, 31,32,33]. Les résultats DMI expérimentaux rapportés de W/CoFeB varient de 0,12 mJ/m ² à 0,73 mJ/m ² [34,35,36]. Dans notre simulation, nous étendons la plage de magnitude DMI à ±2 mJ/m ² pour une étude générale.

L'énergie RKKY entre une paire de moments magnétiques m _i et m _j est défini comme E _ij = σ [1 − m _i m _j ]/∆ _ij , où m _i et m _j sont des moments magnétiques de FL1 et FL2, respectivement. σ est le coefficient d'échange surfacique bilinéaire entre deux surfaces. ∆ _ij est la taille de la cellule de discrétion dans la direction de la cellule i vers la cellule j . Dans ce travail FL1 et FL2 sont couplés ferromagnétiquement, alors σ> 0 ce qui signifie que l'interaction RKKY tend à faire m _i parallèle à m _j . Le DMI agit sur les spins atomiques voisins S ₁ et S ₂ à travers un troisième atome avec un grand SOC. L'hamiltonien DMI correspondant est exprimé par H _DM =  − D ₁₂ (S ₁ × S ₂ ), où D ₁₂ est le vecteur DMI [37]. Par conséquent, le DMI dégrade l'uniformité entre S ₁ et S ₂ , qui entre en concurrence avec l'interaction RKKY.

Résultats et discussion

Tout d'abord, les résultats de simulation typiques du m dépendant du temps _z (composante perpendiculaire de l'aimantation unitaire) sont représentés sur la figure 1b. Si l'interaction RKKY est suffisamment forte (par exemple, σ = 1 × 10 ⁻³ J/m ² dans le cas A et le cas B), FL1 et FL2 sont couplés ensemble et donc leurs dynamiques d'aimantation sont quasiment identiques, que l'on considère ou non le DMI. On voit également que l'introduction de DMI fausse le processus de commutation de magnétisation (voir cas B), ce qui est en accord avec les résultats rapportés [21,22,23] et peut être attribué à l'échange antisymétrique de DMI. Une fois que l'interaction RKKY n'est pas assez forte, la dynamique d'aimantation de FL1 et FL2 ne peut pas être idéalement couplée de sorte qu'une différence significative entre elles est observée (voir cas C). Ci-dessous, les résultats de la simulation sont obtenus sous une interaction RKKY suffisamment forte, sauf indication contraire.

Ensuite, nous étudions la vitesse de commutation sous les différentes interactions RKKY. La vitesse de commutation se traduit par un temps où m _z atteint 0 (défini comme le temps de commutation). Le D ₁ et D ₂ sont respectivement réglés sur des valeurs positives et négatives [29]. Les résultats correspondants sont présentés sur la figure 2. En l'absence de DMI, le temps de commutation augmente avec l'interaction RKKY renforcée, en accord avec les autres résultats rapportés [26,27,28, 38]. La raison en est que l'interaction RKKY plus forte rend la dynamique d'aimantation de FL1 et FL2 plus cohérente, ce qui augmente de manière équivalente l'anisotropie de la couche libre composite. Cependant, la dépendance du temps de commutation sur la force RKKY devient plus chaotique en présence de DMI. Ce chaos est principalement attribué à l'incohérence de l'anisotropie entre FL1 et FL2. Plus d'explications seront montrées plus tard. Ces résultats mettent en évidence l'effet non négligeable du DMI sur le comportement de commutation du MTJ à double interface.

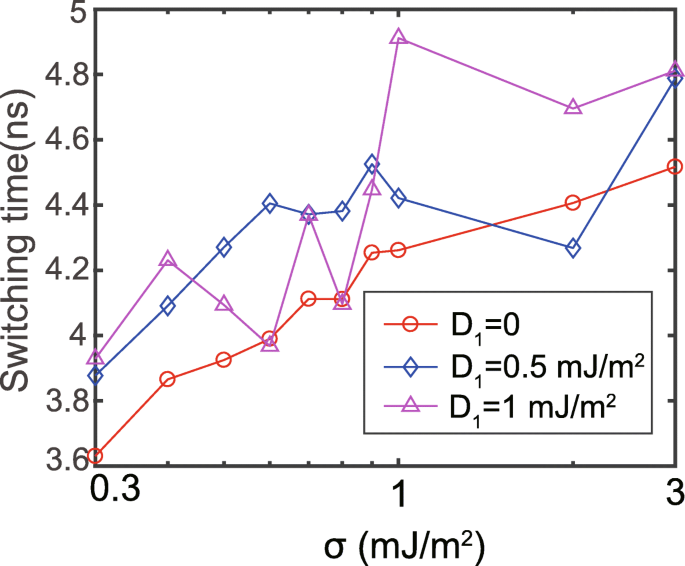
Temps de commutation en fonction de la force RKKY, avec σ affiché dans l'échelle logarithmique. D ₁ et D ₂ sont réglés sur les mêmes valeurs, mais avec les signes opposés

Ensuite, nous étudions plus en détail l'effet du DMI. La figure 3 montre le temps de commutation en fonction de la force DMI. Il est important de mentionner que D ₁ et D ₂ sont intentionnellement fixés aux mêmes valeurs positives dans la figure 3a, bien qu'ils aient les signes opposés en réalité. Autrement dit, la figure 3a correspond à un cas virtuel, que nous étudions pour vérifier le modèle de simulation. Du point de vue de la théorie physique, les effets néfastes de deux DMI positifs sont cumulés sous l'action de l'interaction RKKY couplée ferromagnétiquement. Par conséquent, le temps de commutation devrait augmenter avec l'augmentation de D ₁ et D ₂ , comme rapporté dans les travaux précédents [21, 22]. Cette analyse est en bon accord avec les résultats présentés sur la figure 3a. Ainsi, la rationalité du modèle de simulation est validée. Contrairement à la figure 3a, les effets néfastes du DMI pourraient être atténués si D ₁ et D ₂ ont les signes opposés, comme le montre la figure 3b, où la variation du temps de commutation est beaucoup plus faible par rapport à la figure 3a. Notez que sur la figure 3b, la courbe n'est pas exactement monotone, la fluctuation locale sera expliquée plus tard. Remarquablement, les effets des DMI à deux interfaces pourraient être annulés en réglant de manière appropriée les amplitudes de D ₁ et D ₂ , comme le montre la figure 3c. Ces résultats peuvent être expliqués en termes de théories de la chiralité comme suit.

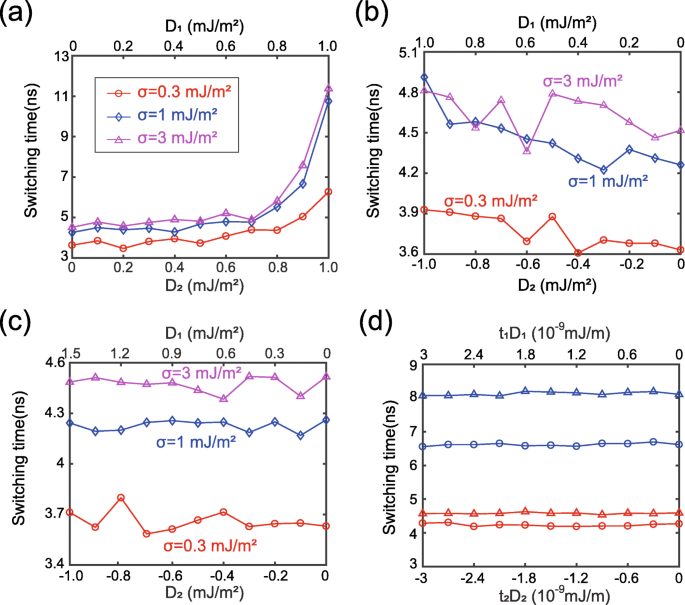
Temps de commutation en fonction de la force DMI. un D ₁ et D ₂ sont mis à la même valeur positive. b D ₁ et D ₂ sont mis à la même valeur, mais avec les signes opposés. c D ₁ et D ₂ sont configurés pour répondre t ₁ D ₁ + t ₂ D ₂ = 0. d Résultats supplémentaires tout en modifiant l'épaisseur ou la constante d'anisotropie, tout en gardant t ₁ D ₁ + t ₂ D ₂ = 0. ligne bleue :t ₁ est changé en 2 nm ; ligne rouge :t ₁ est changé en 1.5 nm. Données triangulaires :σ = 3 × 10 ⁻³ J/m ² . Données du cercle :σ = 1 × 10 ⁻³ J/m ²

L'énergie DMI est exprimée par E _DM = t ∬ D [m _x (∂m _z /∂x ) − m _z (∂m _x /∂x ) + m _y (∂m _z /∂y ) − m _z (∂m _y /∂y )]d ² r = tDε _DM [39], où D est la constante DMI continue, t est l'épaisseur de la couche ferromagnétique. Comme mentionné ci-dessus, les dynamiques d'aimantation de FL1 et FL2 sont presque identiques sous une interaction RKKY suffisamment forte. Dans ce cas, le même ε _DM est obtenu en FL1 et FL2. Ensuite, l'énergie DMI totale de FL1 et FL2 pourrait être calculée par E _tot = (t ₁ D ₁ + t ₂ D ₂ )ε _DM . Par conséquent, en définissant D ₁ /D ₂ =  − t ₂ /t ₁ , les effets DMI de FL1 et FL2 pourraient être complètement compensés dans le cas d'un suffisamment grand, en accord avec la Fig. 3c. Cette conclusion est encore vérifiée par les résultats supplémentaires présentés sur la figure 3d, où les autres paramètres sont intentionnellement modifiés tout en gardant D ₁ /D ₂ =  − t ₂ /t ₁ .

La magnitude DMI équivalente (D _éq ) de la couche libre composite peut être exprimé par D _éq = (t ₁ D ₁ + t ₂ D ₂ )/(t ₁ + t ₂ ), qui pourrait être utilisé pour analyser quantitativement l'effet du DMI sur le MTJ à double interface. Pour valider l'efficacité de cette équation, nous montrons deux groupes de résultats de simulation sur la figure 4a, où deux courbes ont été obtenues sous le même D _éq mais avec deux paires de {D différents ₁ , D ₂ } valeurs, respectivement. Bien qu'il y ait une petite différence entre les deux courbes, leurs tendances globales sont similaires et valident l'effet néfaste du DMI sur la commutation STT. Ici, la différence entre deux courbes pourrait s'expliquer comme suit. FL1 et FL2 ont des constantes d'anisotropie différentes, conduisant à l'oscillation locale incertaine de la dynamique de magnétisation, comme le montre la figure 4c. Le même phénomène est également observé sur la figure 2 et la figure 3b. Au lieu de cela, un cas idéal est illustré sur les figures 4b, d, où les constantes d'anisotropie de FL1 et FL2 sont définies sur les mêmes valeurs. Clairement, une bonne coïncidence entre les deux courbes est observée, indiquant que l'expression ci-dessus de D _éq pourrait bien décrire l'effet DMI équivalent du MTJ à double interface.

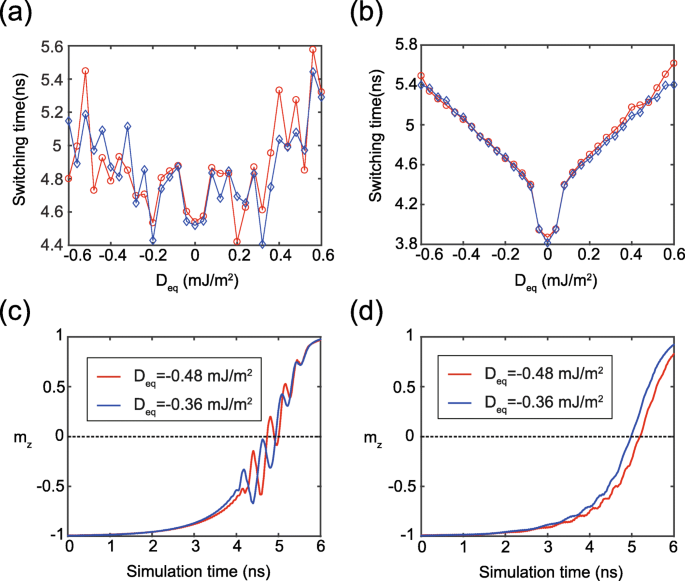
un , b Temps de commutation en fonction de D _éq . Chaque D _éq est obtenu avec deux paires de {D différents ₁ , D ₂ } valeurs selon D _éq = (t ₁ D ₁ + t ₂ D ₂ )/(t ₁ + t ₂ ). Courbe rouge :D ₁ est varié quant à lui D ₂ est fixé à 1 mJ/m ² . Courbe bleue :D ₁ et D ₂ sont toujours mis à la même valeur. Ici σ = 1 × 10 ⁻² J/m ² . Dans a , les autres paramètres sont configurés comme Tableau 1. Dans b , K _{u 1} = K _{u 2} = 0,7 mJ/m ³ pour un cas idéal. c , d Résultats typiques de m dépendant du temps _z correspondant à a et b , respectivement

Enfin, nous analysons plus en détail l'évolution temporelle de la dynamique d'aimantation. La figure 5 montre l'énergie en fonction du temps pendant la commutation de magnétisation. Les énergies DMI du FL1 et FL2 sont accumulées ou annulées, selon les signes et les grandeurs de D ₁ et D ₂ . Cette tendance est en bon accord avec les modèles théoriques ci-dessus. De plus, les énergies RKKY sont maintenues à des valeurs faibles, ce qui valide que les moments magnétiques de FL1 et FL2 sont entraînés de manière synchrone. Les distributions des champs RKKY et DMI sont illustrées sur la figure 6, où le champ RKKY joue différents rôles dans divers cas. Premièrement, dans le cas d'un DMI non nul (voir cas 2 et cas 3), le champ RKKY est beaucoup plus fort par rapport au cas d'un DMI nul (voir cas 1). On peut comprendre que le champ RKKY doit surmonter la non-uniformité supplémentaire des textures magnétiques en présence de DMI. Deuxièmement, si D ₁ et D ₂ sont de signes opposés, le champ RKKY résiste aux champs DMI à la fois dans FL1 et FL2 (voir cas 2). En conséquence, le DMI est affaibli de sorte que la dynamique de magnétisation devient plus uniforme. En revanche, une fois D ₁ et D ₂ ont le même signe, le champ RKKY résiste au champ DMI dans une couche ferromagnétique mais l'assiste dans l'autre couche ferromagnétique (voir cas 3). Ainsi le champ DMI global a encore un certain effet sur la dynamique d'aimantation, ce qui valide que le DMI ne peut pas être annulé si D ₁ et D ₂ sont du même signe.

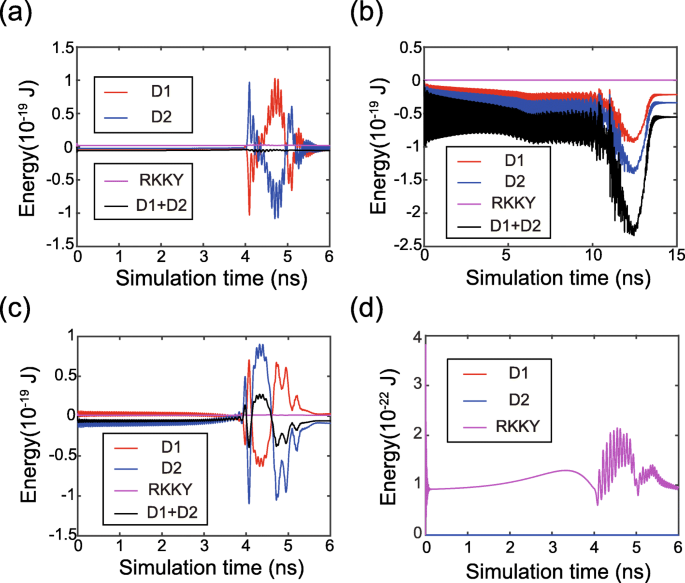
Evolution temporelle des énergies DMI et RKKY. un D ₁ = 1,5 mJ/m ² , D ₂ =  − 1 mJ/m ² , c'est-à-dire que l'effet DMI est annulé. b D ₁ = D ₂ = 1 mJ/m ² , c'est-à-dire que l'effet DMI est accumulé. c D ₁ = 1 mJ/m ² , D ₂ =  − 1 mJ/m ² , c'est-à-dire que l'effet DMI est atténué mais pas annulé. d D ₁ = D ₂ = 0

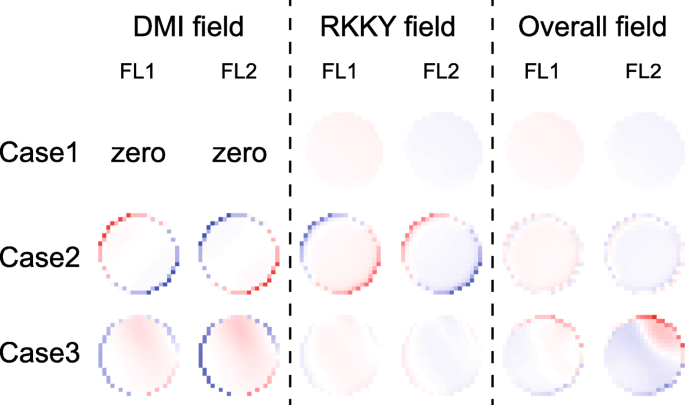
Distributions spatiales des champs DMI et RKKY. Ici, un résultat typique à un moment donné est affiché pour chaque cas. La conclusion reste inchangée aux autres moments. Cas 1 :D ₁ = D ₂ = 0. Cas 2 :D ₁ = 1,5 mJ/m ² , D ₂ =  − 1 mJ/m ² , c'est-à-dire que l'effet DMI est annulé. Cas 3 :D ₁ = D ₂ = 1 mJ/m ² , c'est-à-dire que l'effet DMI est accumulé

La figure 7 montre les configurations micromagnétiques des FL1 et FL2 pendant la commutation de magnétisation. Bien que la paroi du domaine apparaisse dans tous les cas, différentes caractéristiques ont pu être observées à certains moments. Il est bien connu que le DMI favorise les textures magnétiques non uniformes. Néanmoins, sur la figure 7, une magnétisation uniforme est toujours formée même en présence de DMI (voir le moment où m _z =  − 0,5 dans le cas 2), tant que l'effet DMI est annulé. Encore une fois, ce résultat valide le modèle théorique ci-dessus. De plus, on voit également que la dynamique d'aimantation est plus non uniforme si D ₁ et D ₂ sont du même signe (voir le cas 3 où le mur de domaine apparaît toujours), en accord avec l'analyse ci-dessus. Nous montrons également quelques résultats simulés avec une MTJ plus petite (voir les deux dernières lignes de la figure 7). La différence de configurations micromagnétiques entre le cas 2 (DMI est annulé) et le cas 3 (DMI n'est pas annulé) est plus notable.

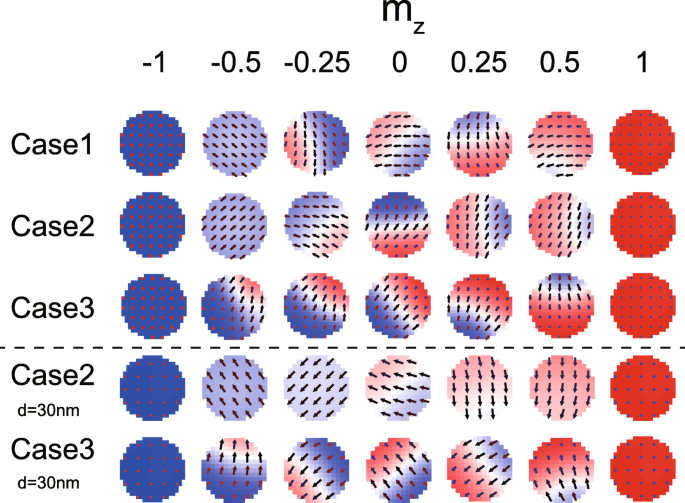
Configurations micromagnétiques lors de la commutation d'aimantation. Ici, les cas 1~3 sont configurés avec les mêmes paramètres que la Fig. 6

Conclusion

Nous avons étudié de manière approfondie l'effet du DMI sur le STT-MTJ à double interface. Comme cela est bien connu, le MTJ à double interface a été développé pour améliorer la barrière de stabilité thermique. Dans ce travail, nos résultats prouvent un autre avantage de la MTJ à double interface, c'est-à-dire la suppression de l'effet néfaste du DMI. Les DMI dans deux couches ferromagnétiques pourraient être supprimées voire annulées si elles sont configurées avec des valeurs appropriées et des signes opposés, ce qui est naturellement satisfait par la structure STT-MTJ à double interface. Des modèles théoriques ont été proposés pour expliquer la conclusion. Les résultats de la simulation micromagnétique ont été discutés pour révéler les rôles de DMI joués dans la dynamique de magnétisation. Notre travail fournit une approche réalisable pour minimiser le DMI dans le STT-MTJ à double interface.

Disponibilité des données et des matériaux

Toutes les données sont entièrement disponibles sans restriction.

Abréviations

DMI :

Interaction Dzyaloshinskii-Moriya

FL :

Couche libre

FM/HM :

Ferromagnétique/métal lourd

MRAM :

Mémoire magnétique à accès aléatoire

MTJ :

Jonction tunnel magnétique

RKKY :

Ruderman–Kittel–Kasuya–Yosida

SOC :

Couplage spin-orbite

STT :

Couple de transfert d'essorage