Polarisation de vallée contrôlable à l'aide de défauts de double ligne de silicone dus au couplage Rashba Spin-Orbit

Introduction

Le silicium, un réseau monocouche en nid d'abeilles à faible flambement d'atomes de silicium, est une alternative potentiellement intéressante au graphène pour les applications valleytronic. La structure à faible flambement donne lieu à un couplage spin-orbite (SOC) relativement important dans le silicène, et un écart énergétique important d'environ 1,55 meV est estimé aux points de Dirac K et K ^′ [1] Différent du graphène, la relation de dispersion à faible énergie du silicène est de forme parabolique plutôt que linéaire. Facilitée par la structure de flambement, la structure de bande du silicène peut être contrôlée en appliquant un champ électrique, et même une transition de phase topologique d'un isolant quantique Hall de spin à un isolant quantique Valley Hall peut se produire[2, 3]. Le silicium a été synthétisé avec succès à la surface de substrats tels que Ag(111), Ir(111) et ZrB2(0001)[4–6], et sa structure autonome stable a également été prédite dans plusieurs études théoriques[7 ]. Plus important encore, un transistor à effet de champ (FET) en silice à température ambiante a été observé avec succès expérimentalement[8]. L'accordabilité du champ électrique et la compatibilité avec les dispositifs existants à base de silicium font du silicène un matériau bidimensionnel potentiel pour une application dans la nouvelle génération de valleytronics.

Dans des matériaux bidimensionnels (2D) tels que le graphène et les dichalcogénures de métaux de transition (MoS₂ , etc.), les joints de grains entre deux domaines de matériau avec des orientations cristallographiques différentes sont des choix idéaux pour atteindre la polarisation de vallée et ont attiré une attention considérable [9-14]. Récemment, les défauts de ligne étendus (ELD) dans le silicène ont été largement étudiés selon les calculs des premiers principes [15, 16], et le 5-5-8 ELD (abrégé en "défaut de ligne" dans ce qui suit) s'est avéré être la structure la plus stable et la plus facile à former. La polarisation de spin et de vallée du défaut de la ligne de silice a été étudiée théoriquement [17–19]. La formation d'un défaut de ligne peut être visualisée comme la couture des bords en zigzag de deux grains de Si par les atomes de Si adsorbés, où chaque côté du défaut de ligne montre un comportement semblable à un état pseudo-arête et les joints de grains du bord en zigzag agissent comme le pseudo-bord [16]. De toute évidence, un tel réseau a une symétrie miroir par rapport à la ligne défaut et les vecteurs de réseau correspondants dans les domaines "gauche" et "droit" séparés par le défaut sont contraires [10, 11]. Dans un tel défaut de ligne avec limite de domaine d'inversion, le A /B les sous-réseaux et les indices de vallée sont échangés lors du franchissement du défaut. Le défaut de ligne est semi-transparent pour les quasiparticules dans le graphène et une polarisation de vallée élevée apparaît avec un angle d'incidence élevé. La polarisation de la vallée est q _y (la vitesse de groupe de l'électron le long du y direction) dépendant à travers le défaut de ligne. Pour le graphène, qui a une dispersion linéaire et une vitesse de groupe constante, la polarisation de la vallée peut atteindre près de 100 % en général |q _y | (correspondant à un angle d'incidence élevé) alors qu'il diminue comme |q _y | diminue et disparaît au fur et à mesure que |q _y |∼0 [9, 14]. En revanche, le silicène a deux caractéristiques de transmission différentes [17, 18] :d'une part, les deux vallées deviennent indiscernables car l'énergie de Fermi est proche du bord de la bande en raison de la relation de dispersion parabolique, et d'autre part, la transmission est restreinte en raison de l'hélice hélicoïdale. état de bord circulant en sens inverse des deux côtés du défaut de ligne, comme le montre la figure 1c. Naturellement, le système avec SOC dans un RSOC particulier est un candidat prometteur pour un FET de spin efficace. Le RSOC génère un champ magnétique effectif dans le plan et induit la précession de spin qui est injectée perpendiculairement au plan de confinement. La polarisation de spin[20] et l'inversion[21] ont été étudiées dans des nanorubans de silice. Des calculs théoriques ont montré que la bande d'énergie du silicène peut être significativement modulée par RSOC [22, 23]. Par exemple, à un RSOC relativement fort, la bande de spin-down (-up) au K (K ^′ ) la vallée se déplace vers le haut tandis que les autres bandes de spin dans la bande de conduction restent inchangées. Compte tenu de la caractéristique de transmission particulière du défaut de la ligne de silice et de l'effet du RSOC dans la silice, les schémas tout électriques pratiques pour générer des porteurs polarisés dans la vallée deviennent réalisables.

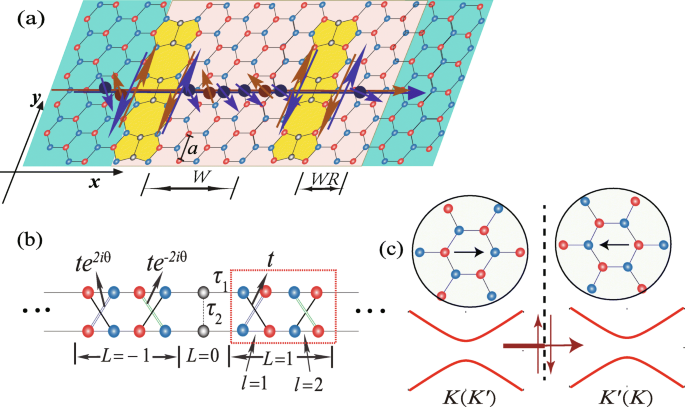
un Schéma de principe du processus de précession des états (K ,↑ )(sphère rouge) et (K ^′ ,↓ )(sphère bleue) à travers une feuille de silice avec deux défauts parallèles, où le cercle bleu (rouge) désigne le A (B ) sous-réseau. Les états (K ,↑ ) et (K ^′ ,↓ ) circulent le long du pseudo-arête, et le RSOC ainsi que le champ électrique sont supposés exister sur la région grise française. W (W =2) et WR (WR =1) représentent la largeur de la région de diffusion en unités de \(\sqrt {3}a\). b Le modèle de réseau simplifié du silicène infini avec un défaut de ligne, où θ =k _y un et le rectangle en pointillé correspond à une supercellule. Dans la maille unitaire, les points du réseau sont spécifiés par un ensemble d'indices (L,l ). c La transmission pour un état de spin dans le K (K ^′ ) vallée à travers le défaut de ligne avec des limites de domaine d'inversion. Les encarts montrent l'orientation du réseau cristallin dans les deux domaines séparés par le défaut de ligne (ligne pointillée). Les lignes épaisses/fines indiquent que la transmission est restreinte à travers le défaut de ligne en raison des états de bord hélicoïdaux circulant en sens inverse le long du pseudo-bord

Dans cet article, nous proposons un moyen efficace de polariser les fermions de Dirac de différentes vallées en utilisant les défauts de double ligne de silice, créant ainsi une polarisation de vallée distincte en utilisant le champ électrique dans la silice. Nos résultats montrent que lorsque l'énergie de Fermi est proche du bas de la bande de conduction, les images d'oscillation des coefficients de transmission de deux vallées, qui comprennent de larges pics oscillants et nadirs, coïncident tant que RSOC dépasse le SOC intrinsèque, tandis que la présence de seulement un seul défaut de ligne ne peut pas disperser les électrons dépendants de la vallée. Lorsque deux défauts de lignes parallèles sont impliqués, les nadirs oscillants évoluent vers des plateaux à transmission nulle, et une modulation efficace du transport dépendant de la vallée peut être réalisée en modifiant la périodicité des oscillations des deux vallées de Dirac avec un champ électrique perpendiculaire, où la périodicité des oscillations de les deux vallées augmentent et diminuent et conduisent à la polarisation parfaite de la vallée dans les régions correspondantes du large plateau pic zéro. Dans l'expérience, on peut détecter un tel courant de vallée pur en mesurant le changement de conductance avec le champ électrique. Ce phénomène fournit une voie différente pour moduler efficacement la polarisation de la vallée dans les dispositifs en silice en utilisant le RSOC et les champs électriques.

Méthodes

Commençons par le schéma d'un dispositif de défaut de ligne de silice à deux bornes, comme le montre la figure 1a, dans lequel la précession de spin est illustrée pour générer le courant polarisé en vallée dû au RSOC et au champ électrique. On suppose que RSOC existe d'un côté du défaut de ligne de largeur W et WR en unités de \(\sqrt {3}a\), où a =3,86 Å est la constante de réseau du silicène vierge, comme le montre la figure 1a. Lorsque l'énergie de Fermi se situe au bas de la bande de conduction, les états (K ,↓ )[ (K ,↓ ) correspond à un état dans la vallée K avec ↓ rotation (vers le bas)] et (K ^′ ,↑ ) sont dans l'écart en raison de la manipulation de la bande d'énergie du RSOC. Les deux autres états, (K ,↑ ) et (K ^′ ,↓ ), circulent le long du pseudo-arête en raison de la caractéristique de verrouillage de l'impulsion de rotation de SOC[24], comme le montre la figure 1a. Pour un état de spin défini, il s'écoule le long du pseudo-bord avec des directions opposées des deux côtés du défaut de ligne qui peut agir comme un filtre et restreindre la transmission à travers le défaut de ligne, comme le montre la figure 1c.

Un modèle de réseau dans la représentation à liaison étroite est utilisé pour décrire le système de défauts de ligne avec RSOC comme [17, 22]

où \(c_{i\alpha }^{\dag }\) et \(c_{i_{y}\alpha,\gamma /\delta }^{\dag }\) représentent l'opérateur de création d'électrons de spin α au site silicène i et le défaut de ligne, respectivement, et 〈〉/〈〈〉〉 s'étend sur tous les sites de saut de voisin le plus proche/suivant. Les trois premiers termes désignent le saut du plus proche voisin et les paramètres t ,τ ₁ , et τ ₂ désignent diverses énergies de saut de voisin le plus proche dans le modèle de liaison étroite, comme le montre la figure 1b. Le quatrième terme est le SOC effectif avec le paramètre de saut t _donc , et ν _ij =±1 pour le saut dans le sens inverse des aiguilles d'une montre (dans le sens des aiguilles d'une montre) entre les sites voisins les plus proches par rapport au z positif -axe. Une enquête théorique [16] a montré que les deux atomes de Si les plus proches dans la région du défaut sont relativement identiques à ceux de la région vierge et que tous les atomes de Si restent dans la sp ² −sp ³ état hybride. Par conséquent, il est raisonnable de définir τ ₂ =τ ₁ =t . Au cinquième mandat, Δ _z est le potentiel de sous-réseau décalé qui résulte d'un champ électrique perpendiculaire à la feuille de silice, et μ _i =±1 pour le A (B ) site. Le dernier terme représente le terme RSOC extrinsèque où t _R est le paramètre de saut de spin-orbite de Rashba. d _ij est le vecteur unitaire pointant depuis le site j à i , et \(\vec {\sigma }=(\sigma ^{x},\sigma ^{y},\sigma ^{z})\) dans l'équation. 1 est le vecteur des matrices de Pauli de spin réel. Le RSOC provient d'un potentiel externe appliqué soit par une grille électrique, soit par l'adsorption d'atomes métalliques, soit par un substrat [20, 25] qui peut considérablement briser la symétrie d'inversion de structure du silicène. Notamment, le RSOC extrinsèque provenant du champ électrique est ignoré car il est très faible.

Les ELD du silicène sont illustrés à la figure 1a, qui s'étend immensément le long du y direction. La symétrie translationnelle de la structure en treillis le long du y direction indique que k _y est une quantité conservée et que les opérateurs de création (annihilation) peuvent être réécrits comme suit, selon la transformation de Fourier (l'indice de spin est ignoré)[17] :

Ensuite, la matrice hamiltonienne dans l'équation. 1 est découplé en \(H=\sum _{k_{y}}H_{k_{y}}\), où \(H_{k_{y}}\) peut être décrit sous la forme suivante :

où \(\varphi _{i,l}^{\dag }=\left [ c_{{{k}_{y}},i,l,A\uparrow }^{\dag }, c_{{{ k}_{y}},i,l,A\downarrow }^{\dag }, c_{{{k}_{y}},i,l,B\uparrow }^{\dag },c_{ {{k}_{y}},i,l,B\downarrow }^{\dag }\right ]\), i dans l'ensemble des index (i,l ) représente la position d'une supercellule \((\bar {i}=-i)\), et l =1 ou 2 désigne différentes chaînes en zigzag dans une supercellule, comme indiqué dans le rectangle en pointillés de la figure 1b. \(\hat {T_{ll'}}\) représente la matrice hamiltonienne de chaque chaîne en zigzag (l =l ^′ ) dans une supercellule ou l'interaction entre différentes chaînes en zigzag (l ≠l ^′ ).

Il est à noter que les deux vallées K et K ^′ sont maintenant lancés à [0,±π /3a ] en raison de l'insertion du défaut de ligne. La matrice de transmission du η (η =K /K ^′ ) la vallée est calculée à l'aide de la formule généralisée de Landauer[26, 27],

où

et

Ici, \(-Im\Sigma _{L,R}=-\left (\Sigma _{L,R}^{r}-\Sigma _{L,R}^{a}\right)/ 2i\ ) sont des matrices semi-définies positives avec une racine carrée matricielle bien définie, où \(\Sigma _{L,R}^{a}=\left [\Sigma _{L,R}^{r}\right ]^{ \dag }\) sont l'auto-énergie retardée/avancée de la dérivation gauche/droite. La sous-matrice 16×16 G ^r est la fonction de Green retardée, qui relie la première et la dernière supercellules le long du x direction et peut être calculé en utilisant la méthode de la fonction de Green récursive. Les coefficients de transmission totaux du η vallée sont \(T_{\eta }=T^{\uparrow \uparrow }_{\eta }+T^{\uparrow \downarrow }_{\eta }+ T^{\downarrow \uparrow }_{\eta }+T^{\downarrow \downarrow }_{\eta }\), et la polarisation de spin P _s et polarisation de vallée P _η peut être donné par

Résultats et discussion

Dans les calculs des coefficients de transmission dépendants du spin, nous définissons τ ₂ =τ ₁ =t =1 comme unité d'énergie, la force SOC t _donc =0.005t , et l'énergie de Fermi E _f =1.001t _donc , qui est situé au bas de la bande de conduction. La largeur de la zone de diffusion est W =1000 pour le défaut de ligne unique et une largeur supplémentaire WR=1000 est également prise en compte pour les deux défauts de lignes parallèles, comme le montre la Fig. 1a.

La figure 2 représente les coefficients de transmission spin-conserved/spin-flip de valley \(\eta, T^{sc}_{\eta }/T^{sf}_{\eta }\), en fonction de l'incident angles α (a) et de la force RSOC t _R (b–d). La figure 2a–c correspond au cas du défaut de ligne simple, et (d) est pour le cas des défauts de deux lignes parallèles. Il est montré qu'à un t défini _R (par exemple, t _R =5t _donc comme sur la Fig. 2a), les coefficients de transmission dépendants du spin \(T^{sc}_{K}/T^{sf}_{K}\) sont constants et indépendants des angles incidents en raison de la relation de dispersion parabolique , comme le montre la figure 2a. Par conséquent, dans les calculs suivants, nous pouvons utiliser l'angle d'incidence α =0 à titre d'exemple. Pour un t faible _R , un phénomène d'oscillation similaire à celui d'un gaz d'électrons bidimensionnel [26, 27] apparaît en raison de la division de Rashba, comme le montre l'encadré de la figure 2b. Comme t _R augmente (t _R >t _donc ), \(T_{K}^{\uparrow \uparrow }\) et \(T_{K}^{\uparrow \downarrow }\) ont la même périodicité d'oscillation et presque les mêmes amplitudes que t _R qui consiste en quelques pics d'oscillation et nadirs, tandis que \(T_{K}^{\downarrow \downarrow }/T_{K}^{\downarrow \uparrow }\) tend vers zéro car l'énergie de Fermi réside dans son écart, comme illustré à la figure 2b. Ainsi, le coefficient de transmission total de K vallée est principalement contribué par l'état de spin up. En fait, les images d'oscillation des deux vallées, K et K ^′ , coïncident alors que les coefficients de transmission de K ^′ La vallée est principalement due aux électrons de spin-down.

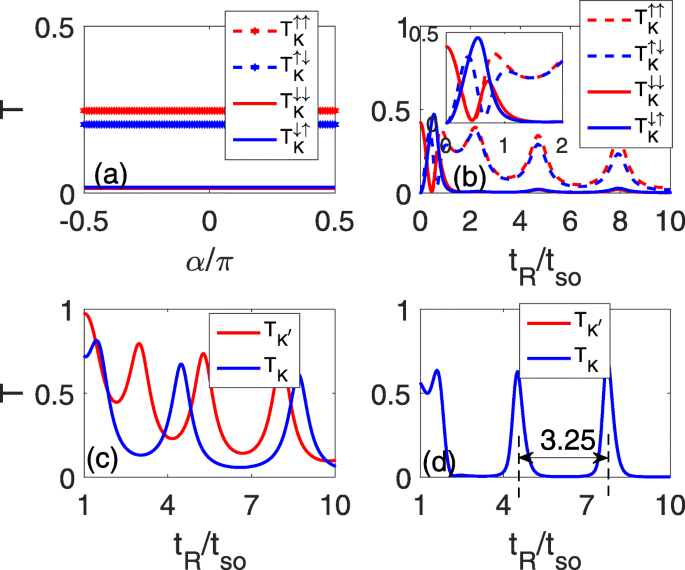
Coefficients de transmission du spin conservé et du spin-flip en fonction des angles incidents α à t _R =5t _donc dans a et en fonction de la force du RSOC t _R en b –d , où a -c sont pour le défaut de ligne simple et d est pour les deux défauts parallèles, avec Δ _z =0.2t _donc en c

En présence d'un champ électrique perpendiculaire, la dégénérescence de la vallée est levée, et les comportements oscillants des deux vallées diffèrent :la périodicité oscillante du K vallée augmente, tandis que celle de la K ^′ la vallée diminue, comme le montre la figure 2c. Cependant, il semble impossible de filtrer un état de vallée conique avec un seul défaut de ligne car les nadirs oscillants ont une amplitude définie. Naturellement, on peut considérer le phénomène d'oscillation avec deux défauts de lignes parallèles pour restreindre davantage la transmission, comme le montre la figure 2d. La comparaison de la figure 2b avec d révèle que le pic d'oscillation devient étroit et aigu, tandis que le nadir d'oscillation s'élargit et s'affaiblit, ce qui forme la plate-forme de transmission zéro. L'espace entre deux pics d'oscillation voisins est fixé à 3,25t _donc , comme caractérisé par les deux lignes pointillées sur la Fig. 2d.

Pour obtenir un meilleur effet de filtre de vallée, nous concentrons notre attention sur l'effet du champ électrique perpendiculaire. Les résultats de cet effet sont montrés sur la figure 3. Comme discuté ci-dessus, la périodicité d'oscillation des deux vallées change d'une manière opposée, et les pics d'oscillation se chevauchant d'origine sur la figure 2d sont atténués. Pendant ce temps, le plateau sans transmission s'élargit et se rétrécit pour T _K et \(T_{K^{\prime }}\), respectivement, comme le montrent les figures 3a et b. À Δ _z =0.15t _donc , l'espace entre les deux pics d'oscillation voisins se développe en 3,6t _donc pour T _K , alors qu'il est réduit à 3.1t _donc pour \(T_{K^{\prime }}\), comme indiqué par les deux lignes pointillées bleues et rouges illustrées à la figure 3a. Au fur et à mesure que le champ électrique se renforce, l'espace entre les deux pics d'oscillation voisins continue d'augmenter/diminuer pour T _K /\(T_{K^{\prime }}\), qui est 5.4t _donc /2.8t _donc à Δ _z =0.3t _donc , comme le montre la figure 3b. Le changement de la périodicité des oscillations conduira aux régions correspondantes du large plateau pic-zéro, où la polarisation parfaite de la vallée avec P _η =±1 plateaux peuvent être réalisés, comme le montrent les Fig. 3c et d. Simultanément, il est montré que la polarisation de spin élevée P _s survient également lorsque P _η =±1.

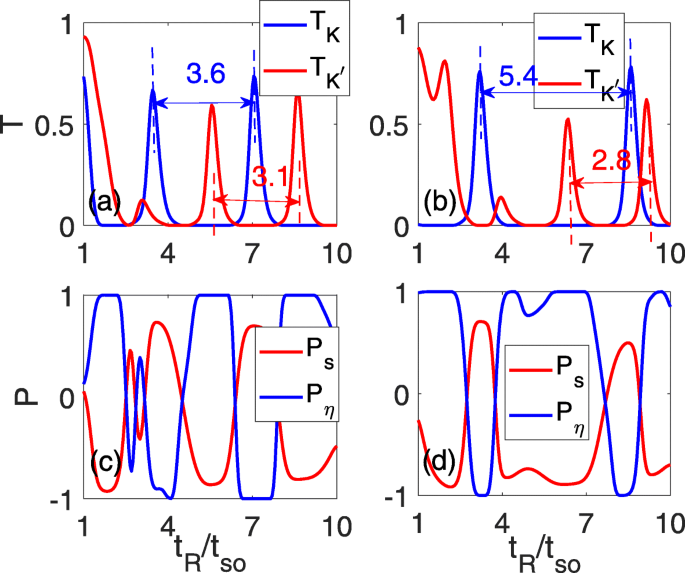
Les coefficients de transmission totaux \(T_{K}/T_{K^{\prime }}\) (a , b ) et la polarisation spin/vallée (c , d ) en fonction de la force RSOC t _R pour différents potentiels de sous-réseau. Δ _z =0.15t _donc dans a et c et Δ _z =0.3t _donc en b et d; les autres paramètres sont identiques à ceux de la Fig. 2d

Cependant, en raison du caractère incontrôlable du RSOC, il est encore difficile de détecter expérimentalement de tels courants de vallée purs, même si le RSOC induit dans le défaut de ligne peut être supérieur au SOC intrinsèque. Pour sonder commodément le courant de vallée pur expérimentalement, nous étudions également les coefficients de transmission et la polarisation de vallée en fonction du champ électrique, qui peut être contrôlé en continu au cours d'une expérience. Il est montré que la polarisation de vallée parfaite avec P _η =±1 peut émerger dans une certaine plage de Δ _z et qu'il peut changer de P _η =1 à P _η =−1 lorsque le champ électrique augmente, comme le montre la figure 4a. Pour un t défini _R (par exemple t _R =7.2t _donc , comme indiqué en pointillé sur la figure 4a), les coefficients de transmission \(T_{K}/T_{K^{\prime }}\) oscillent avec Δ _z , où les larges pics de transmission du K (K ^′ ) vallée correspondent aux plateaux à transmission nulle du K ^′ (K ) vallée. Les coefficients de transmission totaux sont essentiellement contribués par une vallée lorsque le champ électrique varie, et une polarisation parfaite de la vallée peut toujours se produire autour de la valeur maximale de \(T_{K}/T_{K^{\prime }}\), comme indiqué dans 4b. Comme l'énergie de Fermi s'éloigne du bord de la bande, la polarisation parfaite de la vallée peut encore survivre même à E _f =1.5t _donc , où la relation de plateau peut être bien maintenue, comme le montre la figure 4c. Au cours d'une expérience, on peut analyser les courants électriques polarisés en vallée de gauche à droite avec une quantité mesurable expérimentalement telle que la conductance, qui est proportionnelle au coefficient de transmission total. La conductance maximale entre deux valeurs minimales (parfois, elles sont nulles) doit provenir d'une vallée. On peut estimer l'amplitude de la conductance selon la formule \(G=\frac {e^{2}}{h}\int _{-k_{F}}^{k_{F}}T\frac {dk_ {y}}{2\pi /L_{y}}=\frac {e^{2}}{h}\frac {Ly\sqrt {E^{2}-t^{2}_{so}} }{2\pi \hbar v_{F}}2T\) [28], où L _y =2a ≈7.72Å est la largeur du défaut de la ligne de silice, v _F =5.5×10 ⁵ m /s est la vitesse de Fermi, \(\hbar =h/2\pi \) est la constante de Planck réduite avec \(\phantom {\dot {i}\!}h=4.13566743\times 10^{-15}eV\cdot s, T=T_{K}+T_{K'}\) est le coefficient de transmission total et E est l'énergie sur site des électrons incidents. Ensuite, la conductance est d'environ \(G\approx \left [0.7T\sqrt {E^{2}-t^{2}_{so}}/eV\right ]\frac {e^{2}}{ h}\). Il est également constaté que lorsque l'énergie sur site du côté incident est élevée à E =0.15t (t =1.6eV ), les coefficients de transmission des deux vallées ne changent que légèrement par rapport à la figure 4c en raison de la conservation du spin et de la quantité de mouvement et la relation pic de transmission-plateau zéro se maintient, comme le montre la figure 4d. Dans ce cas, la conductance est d'environ \(G\environ 0,17T\frac {e^{2}}{h}\) ce qui est important et peut être détectable expérimentalement. La fenêtre énergétique pour observer ce phénomène est d'environ 0,5t _donc (t _donc <E <1.5t _donc ) qui est proportionnel à t _donc . Dans l'expérience, il n'est pas difficile de contrôler l'énergie de Fermi près du bord de la bande et l'écart SOC peut même être radicalement augmenté à 44 meV par proximité avec la bicouche Bi (111) [29] qui peut grandement améliorer la région d'énergie pour détecter le pur courant de la vallée. De plus, le modèle de calcul peut également être applicable à d'autres homologues à faible flambement du graphène, du germanène[30], du stanène et du MoS₂ [31–36], qui ont des bandes interdites encore plus grandes [37, 38] ainsi que les forces SOC (la force SOC peut atteindre 0,1 eV pour le stanène [38, 39]). Dans une expérience réelle, il est facile de réaliser un RSOC fort qui peut dépasser le SOC intrinsèque en brisant la symétrie du miroir dans le plan avec le substrat spécial [40]. Par conséquent, ce schéma peut être tout à fait réalisable en expérimentation.

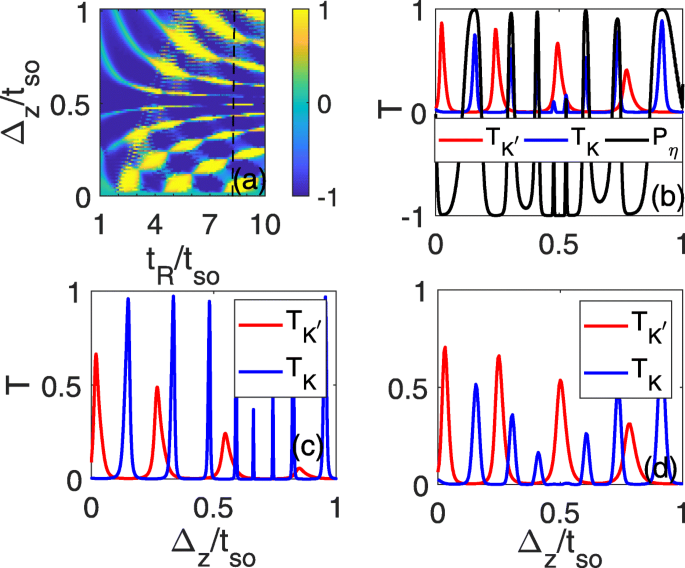
Polarisation de la vallée a et \(T_{K}/T_{K^{\prime }}\) (b –d ) en fonction de Δ _z et t _R . t _R =7.2t _donc dans (b –d ), E _f =1.5t _donc en c et d , et l'énergie sur site est E =0.15t dans l'électrode gauche en d; tous les autres paramètres sont identiques à ceux de la Fig. 2d