ARTICLE RÉTRACTÉ :Les protocoles de communication directe bidirectionnelle peuvent-ils être considérés comme sécurisés ?

Contexte

La cryptographie quantique, en particulier les protocoles de distribution de clés quantiques (QKD), nous offre, contrairement au protocole classique, une communication probablement incassable basée sur les propriétés physiques quantiques des supports d'information [8, 23, 25]. Jusqu'à présent, les implémentations étaient principalement basées sur le protocole BB84 [2] qui est inconditionnellement sécurisé à condition que le taux d'erreur quantique sur les bits (QBER) soit suffisamment bas. Cependant, le QBER dans les protocoles de type BB84 peut être élevé, et comme nous ne pouvons pas distinguer les inversions de bits des espions (Eve) des inversions de bits causées par des pertes et des imperfections, la demande d'avoir un QBER suffisamment bas pour traiter les bits est souvent difficile à satisfaire, par exemple , BB84 à 4 états avec plus de 11 % [26] et BB84 à 6 états [5] avec plus de 12,6 % [26] de perturbation (D ) doivent être annulés (D est défini comme le pourcentage de basculements de polarisation provoqués par Eve, le maximum étant de 0,5). Depuis le D ne peut pas être discriminé du QBER inhérent à la ligne, ces niveaux de QBER total sont peu sûrs (informations mutuelles entre l'expéditeur (Alice) et Eve (I _AE ) surpasse celui entre Alice et le receveur (Bob) (I _AB ):Je _AE>Je _AB pour D>0.11,0.126, respectivement) et ne peut donc pas être effectuée simplement parce qu'Eve pourrait être dans la file.

À la recherche de protocoles plus efficaces, des protocoles bidirectionnels ont été proposés et mis en œuvre. En particulier, les protocoles bidirectionnels de photons intriqués basés sur deux [4] (également appelés ping-pong (pp) protocole) et quatre (Ψ ^∓ ,Φ ^∓ ) [6] Bell énonce, d'une part, et un protocole Lucamarini-Mancini (LM05) déterministe à photon unique, d'autre part [1, 19]. Plusieurs variétés, modifications et généralisations de ce dernier protocole sont données dans [11, 12, 24, 27]. Deux variétés ont été implémentées dans [7] and [14]. L'ancien protocole pp a été mis en œuvre par Ostermeyer et Walenta en 2008 [22] tandis que le protocole à quatre états de Bell ne peut pas être mis en œuvre avec des éléments d'optique linéaire [20, 29]. Dans les références susmentionnées, diverses estimations de sécurité ont été obtenues.

Dans [17], Lu, Fung, Ma et Cai fournissent une preuve de sécurité d'un QKD déterministe LM05 pour le type d'attaque proposé dans [1, 19]. Néanmoins, ils prétendent qu'il s'agit d'une preuve de la sécurité inconditionnelle de LM05. Dans [10], Han, Yin, Li, Chen, Wang, Guo et Han fournissent une preuve de sécurité pour un protocole pp modifié et prouvent sa sécurité contre les attaques collectives dans un canal bruyant et avec perte.

Toutes les considérations sur la sécurité des protocoles bidirectionnels supposent qu'Eve attaque chaque signal deux fois, une fois sur le chemin de Bob à Alice, et plus tard sur le chemin du retour d'Alice à Bob, et que, ce faisant, elle perturbe le signal dans le mode messages. Cependant, comme nous le montrons ci-dessous, il existe d'autres attaques dans lesquelles une Eve indétectable encode les signaux de Bob selon l'encodage d'Alice d'un signal leurre qui lui est envoyé et plus tard lu par Eve.

Dans cet article, nous montrons que dans les protocoles QKD déterministes bidirectionnels sous une attaque d'interception et de renvoi particulière, une Eve indétectable peut acquérir tous les messages en mode message (MM) et que l'information mutuelle entre Alice et Bob est constante et égale. à une. Cela signifie que la sécurité des protocoles ne peut pas être établie via des procédures standard d'évaluation de la fraction secrète des longueurs de clé.

Méthodes

Nous analysons les attaques sur deux protocoles QKD bidirectionnels différents :à photon intriqué et à photon unique. En particulier, nous détaillons la procédure qui permet à Eve de lire tous les messages en mode message tout en restant indétectable. Par la suite, nous procédons à une analyse de sécurité, afin de calculer une information mutuelle entre Alice et Eve, ainsi qu'entre Alice et Bob, en fonction de la perturbation qu'Eve pourrait introduire lors de l'écoute. Finalement, nous appliquons les résultats obtenus sur la procédure qui vise à prouver une sécurité inconditionnelle des protocoles bidirectionnels.

Résultats et discussion

Protocoles bidirectionnels de photons enchevêtrés

Nous considérons un protocole bidirectionnel à photons intriqués basé sur deux états de Bell (protocole pp) [4]. Bob prépare des photons intriqués dans l'un des états de Bell et envoie l'un des photons à Alice et conserve l'autre dans une mémoire quantique. Alice renvoie le photon tel quel ou agit dessus de manière à mettre les deux photons dans un autre état de Bell. La cloche déclare qu'elle envoie de cette manière ses messages à Bob. Bob combine le photon qu'il reçoit d'Alice avec celui qu'il a gardé, et à un séparateur de faisceau (BS), il décode les messages d'Alice. De tels messages sont censés être envoyés dans un mode message (MM). Il existe également un mode de contrôle (CM) dans lequel Alice mesure le photon de Bob. Elle annonce le basculement entre les modes sur une chaîne publique ainsi que les résultats de ses mesures en CM.

Nous définissons la base Bell comme une base constituée de deux états Bell

où |H 〉 _i (|V 〉 _i ), i =1,2, représentent les états de photons polarisés horizontaux (verticaux).

Paires de photons dans l'état |Ψ ⁻ sont générés par une source de photons intriqués down-convertie. Pour envoyer |Ψ ⁻ état Alice renvoie juste son photon à Bob. Pour envoyer |Ψ ⁺ 〉, elle place une lame demi-onde (HWP(0°)) sur le trajet de son photon, comme le montre la figure 1b. Le HWP change le signe de la polarisation verticale.

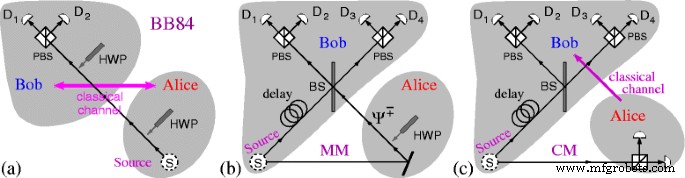
Schémas des protocoles BB84 et ping-pong (pp). un BB84 :les canaux classiques et quantiques sont fusionnés. b MM du protocole pp — canal quantique. c CM du protocole pp—canal classique

Chez Bob's BS, les photons en état |Ψ ⁻ 〉 se séparera et ceux en état |Ψ ⁺ se regroupera.

Eve effectue son attaque, conçue par Nguyen [21], comme suit :>Ψ ⁻ 〉 comme le montre la figure 2. Quand Eve reçoit le photon d'Alice, elle le combine avec l'autre photon de la paire et détermine l'état de Bell de la même manière que Bob le ferait. Elle utilise ce résultat pour générer le même état Bell pour Bob en plaçant les HWP appropriés sur le chemin du photon de Bob.

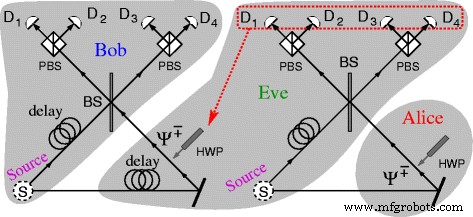
Attaque de Nguyen [21] sur le protocole pp. Eve est capable de copier de manière déterministe chacun des messages d'état de Bell dans le mode message du protocole pp

Ainsi, Eve est capable de copier chaque message en MM et donc l'envoi de messages en MM équivaut à l'envoi de texte en clair "sécurisé" par CM. Nous reviendrons sur ce point plus tard.

Ici, nous soulignons que les photons couvrent quatre fois la distance qu'ils couvrent dans BB84. Donc, si la probabilité qu'un photon soit détecté sur la seule distance Bob-Alice est p , la probabilité d'être détecté sur la distance Bob-Alice-Bob sera de p ⁴ ce qui, avec l'augmentation exponentielle des pertes sur la distance, diminue également de manière exponentielle la probabilité de détecter la perturbation qu'Eve introduit dans CM.

Protocoles bidirectionnels à photon unique

Nous commençons par une brève présentation du protocole LM05 [18, 19]. Comme le montre la figure 3, Bob prépare un qubit dans l'un des quatre états |0〉, |1〉 (le Pauli Z états propres), |+〉, ou |−〉 (Pauli X états propres) et l'envoie à son homologue Alice. Dans le MM, elle modifie l'état du qubit en appliquant soit I , qui laisse le qubit inchangé et encode le 0 logique , ou en appliquant i Oui =Z X , qui inverse l'état du qubit et encode le 1 logique . (i Oui |0〉=−|1〉,i Oui |1〉=|0〉,i Oui |+〉=|−〉,i Oui |−〉=−|+〉.) Alice renvoie maintenant le qubit à Bob qui le mesure dans la même base dans laquelle il l'a préparé et en déduit de manière déterministe les opérations d'Alice, c'est-à-dire ses messages, sans procédure de réconciliation de base.

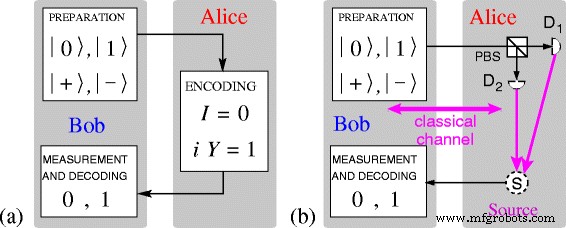
Protocole LM05. un Mode message (MM) selon [19, Fig. 1]. b Mode de contrôle

L'attaque du protocole LM05 que nous considérons est proposée par Lucamarini dans [18, p. 61, figure 5.5]. Elle est illustrée à la figure 4. Eve retarde le photon de Bob (qubit) dans une bobine de fibre (une mémoire quantique) et envoie son propre photon leurre dans l'un des quatre états |0〉, |1〉, |+〉 ou | −〉 à Alice, à la place. Alice encode son message via I ou i Oui et renvoie le photon. Eve le mesure dans la même base dans laquelle elle l'a préparé, lit le message, encode le photon retardé de Bob via I , si elle lit 0 , ou via i Oui , si elle a lu 1 , et le renvoie à Bob.

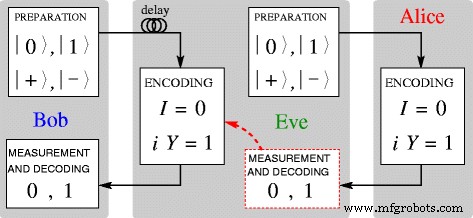
L'attaque de Lucamarini sur le protocole LM05. Les schémas sont faits selon [18, p. 61, fig. 5.5]

Eve n'apprend jamais les états dans lesquels Bob a envoyé ses photons mais cela n'a pas d'importance dans le MM puisque seul le retournement de polarisation ou non encode les messages. Alice n'a pas non plus besoin de connaître les états de Bob [19]. Cela signifie qu'Eve n'a pu être révélé qu'en CM dans lequel Alice effectue une mesure projective du qubit selon une base choisie aléatoirement entre Z et X , prépare un nouveau qubit dans le même état que le résultat de la mesure, le renvoie à Bob et le révèle sur un canal public classique [19], comme le montre la figure 4.

Ici, il convient de souligner que les photons dans LM05 couvrent deux fois la distance qu'ils couvrent dans BB84. Donc, si la probabilité qu'un photon soit détecté sur la seule distance Bob-Alice est p , la probabilité d'être détecté sur la distance Bob-Alice-Bob sera de p ² et Eve serait capable de se cacher exponentiellement mieux dans CM que dans BB84.

Sécurité des protocoles bidirectionnels

Dans un protocole BB84 avec plus de 11% de perturbation, l'information mutuelle entre Alice et Eve I _AE est supérieur à l'information mutuelle entre Alice et Bob I _AB et il faut l'interrompre.

Pour nos attaques, il n'y a pas de perturbation (D ) qu'Eve induit dans MM et l'information mutuelle entre Alice et Bob est égale à l'unité.

Par conséquent, contrairement à BB84, I _AB et Je _AE ne sont pas des fonctions de D et cela nous empêche de prouver la sécurité en utilisant l'approche standard.

De plus, dans une mise en œuvre réaliste, il n'y a pas de D significatif en MM non plus. Lorsque Bob, par exemple, envoie un photon dans |H 〉 et Alice ne le change pas, alors Bob détectera |H avec une probabilité proche de 1, avec ou sans Eve, et indépendamment de la distance. Le seul QBER qui dépend de la longueur de la fibre est celui qui provient des comptages d'obscurité des détecteurs [28]. Dans une mise en œuvre récente d'un QKD unidirectionnel, le QBER total était inférieur à 2 % sur une distance de 250 km [13]. Nous pouvons pratiquement éliminer complètement les comptes d'obscurité, et donc tout retournement de polarisation incontrôlé, en utilisant des détecteurs de photons supraconducteurs à bord de transition (TES). L'efficacité la plus élevée de ces détecteurs est actuellement supérieure à 98 % [9, 15, 16], et leur probabilité de comptage d'obscurité est pratiquement nulle.

Pour BB84, et pratiquement tous les protocoles unidirectionnels à un photon récemment mis en œuvre ou envisagés pour la mise en œuvre, la sécurité des protocoles est évaluée via le QBER critique en calculant la fraction secrète [26]

où l est la longueur de la liste constituant la clé finale et n est la longueur de la liste constituant la clé brute, I _AB =1+D log2D +(1−D ) log2(1−D ) et Je _AE =−D log2D −(1−D ) log2(1−D ) et leur intersection donne D =0.11. De manière équivalente, r =1+2D log2D +2(1−D ) log2(1−D ) descend à 0 lorsque D atteint 0,11.

Nous n'avons pas une telle option pour nos attaques sur les protocoles bidirectionnels car elle découle de Eqs. (2) et (3) que r n'est jamais négatif. En fait, il ne s'approche de 0 que lorsqu'Eve est dans la file tout le temps.

Depuis le D n'est en aucun cas lié au mode MM, c'est à Alice et Bob de décider après quoi D ils interrompraient leur transmission. Cependant, quel que soit le 0≤D ≤0,5 ils choisissent, I _AB −Je _AE seront toujours non négatifs et n'auront pas de valeur critique D comme dans BB84 où les courbes I _AB (D ) et Je _AE (D ) se coupent pour D =0,11 en MM comme indiqué sur la figure 5a. Pour les protocoles déterministes bidirectionnels, le niveau de D , qui est défini dans CM (et non dans MM), n'a aucun effet sur I _AB , c'est-à-dire qu'il n'y a aucune différence si D =0 ou D =0,5, comme illustré sur la figure 5b ; 0≤D <0,5 signifierait seulement qu'Eve n'est pas dans la file tout le temps, mais Bob obtient toujours des informations complètes d'Alice :quand Eve n'est pas dans la file, parce qu'elle n'est pas dans la file, et quand Eve est dans la file, parce qu'elle transmet fidèlement tous les messages d'Alice à Bob.

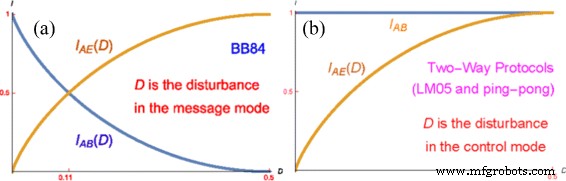
Tracés d'informations mutuelles pour BB84 par rapport aux protocoles déterministes bidirectionnels. un Protocole probabiliste unidirectionnel BB84. b Protocoles déterministes bidirectionnels avec des états de Bell intriqués ou avec des états à photon unique de type LM05. La différence essentielle entre eux est que dans a Eve provoque des retournements de polarisation dans le mode message, tandis qu'en b Eve ne provoque idéalement aucun retournement en mode message

On peut supposer qu'Eve n'arrache qu'une partie des messages afin de maintenir QBER dans CM à un niveau bas (et avoir I _AE ≤1) qui serait acceptable pour Alice et Bob. Dans cet esprit, nous pouvons essayer d'effectuer l'évaluation de la sécurité de notre attaque et vérifier si les preuves de sécurité inconditionnelle effectuées pour d'autres types d'attaques sur LM05 dans [1, 17] pourraient également s'appliquer à celle-ci.

Dans la preuve de sécurité susmentionnée [17], qui est prétendument inconditionnelle , les auteurs d'abord, dans la Sec. III.A, prétendez qu'Eve doit attaquer les qubits dans les canaux Bob-Alice et Alice-Bob pour obtenir les bits de clé d'Alice, et dans Sec. III.B, Éq. (1,3), ils supposent qu'Eve lit le qubit de Bob et induit une perturbation dans le mode message dans les canaux Bob-Alice et Alice-Bob (taux d'erreur e; dernier paragraphe de la Sec. III.B et premier alinéa de la Sec. III.F).

Cependant, dans les attaques envisagées, Eve ne mesure Les qubits de Bob. Elle les stocke simplement dans une mémoire quantique. Elle envoie ses propres qubits à Alice et lit si elle les a modifiés (O ) ou non (Je ). Ensuite, elle applique O ou Je pour stocker les qubits de Bob et les lui renvoie. Par conséquent, elle n'induit pas non plus de perturbation dans le canal Alice-Bob. De plus, elle n'utilise aucune ancilla comme dans [17]. Par conséquent, l'analyse de l'obtention des bits de clé effectuée dans [17] est inapplicable à notre attaque.

Par conséquent, puisque la preuve de sécurité présentée dans [17] s'applique uniquement à l'attaque considérée et non à l'attaque de Lucamarini ci-dessus, elle n'est pas universelle, c'est-à-dire qu'elle ne peut pas être considérée comme inconditionnelle .

Voyons maintenant si une procédure standard connue peut être utilisée pour établir la sécurité du protocole LM05. Dans le protocole, nous n'avons ni tamisage ni taux d'erreur dans le mode message. Ainsi, le rapprochement d'erreur standard ne peut pas non plus être appliqué.

La seule procédure qui nous reste pour établir la sécurité est l'amplification de la confidentialité. Lorsqu'Eve ne possède qu'une fraction des données, elle perd la trace de ses morceaux et ceux d'Alice et de Bob rétrécissent. Eve pourrait peut-être récupérer des données en devinant les bits qu'elle manque et réintroduit tous les bits dans la fonction de hachage. En cas d'échec, ses informations seront en partie effacées. Cependant, Alice et Bob rencontrent un problème crucial lors de la conception de leur procédure de sécurité (par exemple, la fonction de hachage) qui garantirait qu'Eve n'aura aucune information sur la clé finale. Ils n'ont pas une quantité critique de bits d'Eve comme dans BB84 (11%) qui sont explicitement inclus dans les équations de la procédure d'amplification de la confidentialité [3].

En un mot, la vie privée qui doit être amplifiée n'est pas bien défini. Concevoir un protocole pour une telle amplification de la confidentialité « aveugle » est une entreprise complexe [3], et la question est de savoir si l'envoi de – en fait – du texte brut via MM sécurisé par une vérification occasionnelle des états des photons dans CM nous offre un avantage par rapport à ou une meilleure sécurité que le protocole BB84.

Dans le tableau 1, nous listons les propriétés d'un protocole de type BB84 sous une attaque arbitraire par rapport aux protocoles bidirectionnels sous les attaques ci-dessus, ce qui semble indiquer qu'il serait difficile de répondre positivement à la question susmentionnée.

Conclusions

Pour résumer, nous avons considéré des attaques déterministes sur deux types de protocoles QKD bidirectionnels (pp avec photons intriqués et LM05 avec photons uniques) dans lesquels une Eve indétectable peut décoder tous les messages en mode message (MM) et avons montré que l'information mutuelle entre Alice et Bob n'est pas une fonction de perturbation mais est égal à l'unité, peu importe si Eve est dans la ligne ou non. Eve induit une perturbation (D ) uniquement dans le mode de contrôle (CM) et donc l'approche standard et les protocoles d'estimation et de calcul de la sécurité ne sont pas disponibles car ils supposent tous la présence de D en MM. En conséquence, un D critique ne peut pas être déterminé, la procédure de correction d'erreur standard ne peut pas être appliquée pour éliminer les informations d'Eve, l'efficacité de l'amplification de la confidentialité est réduite et la sécurité inconditionnelle ne peut pas être considérée comme prouvée. D'une certaine manière, l'envoi de la clé par Alice équivaut à l'envoi d'un texte clair non crypté « sécurisé » par un indicateur peu fiable de la présence d'Eve et de tels protocoles ne peuvent pas être envisagés pour la mise en œuvre du moins pas avant de prouver ou de réfuter qu'un nouveau type de procédures de sécurité pour de telles attaques déterministes peuvent être conçues.

Nous soulignons que pour décider si un protocole est inconditionnellement sécurisé ou non, il importe peu qu'Eve puisse effectuer des attaques plus efficaces que les attaques considérées ci-dessus, pour un D choisi. en CM . Une preuve de sécurité inconditionnelle devrait les couvrir tous.

Historique des modifications