Entraînement d'ensembles de données pour les réseaux de neurones :comment entraîner et valider un réseau de neurones Python

Dans cet article, nous utiliserons des exemples générés par Excel pour entraîner un Perceptron multicouche, puis nous verrons comment le réseau fonctionne avec des exemples de validation .

Si vous cherchez à développer un réseau de neurones Python, vous êtes au bon endroit. Avant d'approfondir la discussion de cet article sur l'utilisation d'Excel pour développer des données d'entraînement pour votre réseau, pensez à consulter le reste de la série ci-dessous pour obtenir des informations générales :

1. Comment effectuer une classification à l'aide d'un réseau de neurones :qu'est-ce que le perceptron ?
2. Comment utiliser un exemple simple de réseau neuronal Perceptron pour classer des données
3. Comment former un réseau de neurones Perceptron de base
4. Comprendre la formation simple sur les réseaux neuronaux
5. Une introduction à la théorie de la formation pour les réseaux de neurones
6. Comprendre le taux d'apprentissage dans les réseaux de neurones
7. Apprentissage automatique avancé avec le Perceptron multicouche
8. La fonction d'activation sigmoïde :activation dans les réseaux de neurones Perceptron multicouches
9. Comment former un réseau de neurones Perceptron multicouches
10. Comprendre les formules d'entraînement et la rétropropagation pour les perceptrons multicouches
11. Architecture de réseau neuronal pour une implémentation Python
12. Comment créer un réseau de neurones Perceptron multicouche en Python
13. Traitement du signal à l'aide de réseaux de neurones :validation dans la conception de réseaux de neurones
14. Entraînement d'ensembles de données pour les réseaux de neurones :comment entraîner et valider un réseau de neurones Python

Qu'est-ce que les données d'entraînement ?

Dans un scénario réel, les échantillons d'entraînement sont constitués de données mesurées d'une sorte combinées avec les « solutions » qui aideront le réseau de neurones à généraliser toutes ces informations dans une relation entrée-sortie cohérente.

Par exemple, disons que vous voulez que votre réseau de neurones prédise la qualité gustative d'une tomate en fonction de sa couleur, sa forme et sa densité. Vous n'avez aucune idée de la corrélation exacte entre la couleur, la forme et la densité et le délice global, mais vous pouvez mesurer la couleur, la forme et la densité, et vous faites avoir des papilles gustatives. Ainsi, tout ce que vous avez à faire est de rassembler des milliers et des milliers de tomates, d'enregistrer leurs caractéristiques physiques pertinentes, de goûter chacune (la meilleure partie), puis de mettre toutes ces informations dans un tableau.

Chaque ligne est ce que j'appelle un échantillon d'apprentissage, et il y a quatre colonnes :trois d'entre elles (couleur, forme et densité) sont des colonnes d'entrée et la quatrième est la sortie cible.

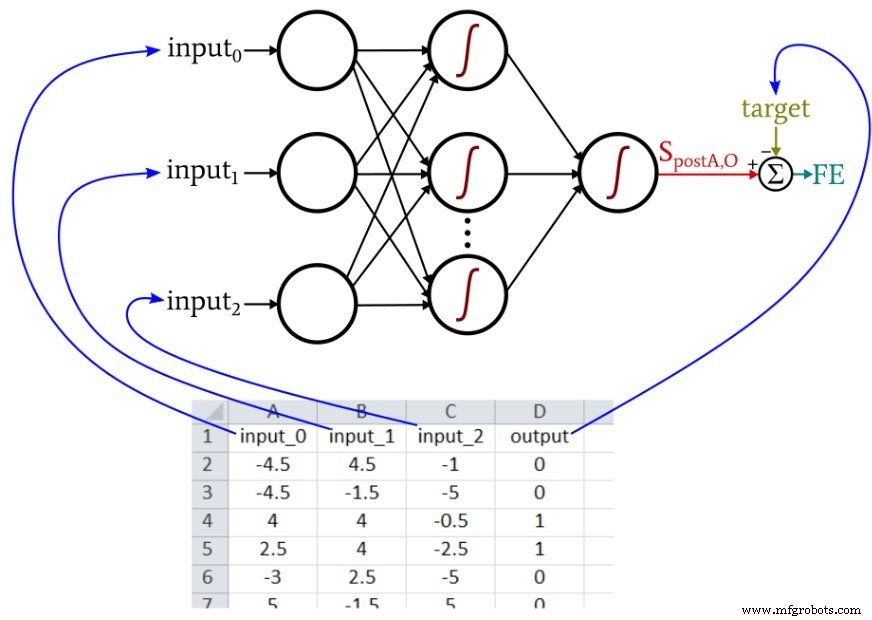
Pendant l'apprentissage, le réseau de neurones trouvera la relation (si une relation cohérente existe) entre les trois valeurs d'entrée et la valeur de sortie.

Quantification des données d'entraînement

Gardez à l'esprit que tout doit être traité sous forme numérique. Vous ne pouvez pas utiliser la chaîne "en forme de prune" comme entrée de votre réseau de neurones, et "l'eau à la bouche" ne fonctionnera pas comme valeur de sortie. Vous devez quantifier vos mensurations et vos classements.

Pour la forme, vous pouvez attribuer à chaque tomate une valeur de -1 à +1, où -1 représente parfaitement sphérique et +1 représente extrêmement allongé. Pour la qualité gustative, vous pouvez évaluer chaque tomate sur une échelle à cinq points allant de « non comestible » à « délectable », puis utiliser un codage à chaud pour mapper les évaluations sur un vecteur de sortie à cinq éléments.

Le diagramme suivant vous montre comment ce type d'encodage est utilisé pour la classification de sortie de réseau de neurones.

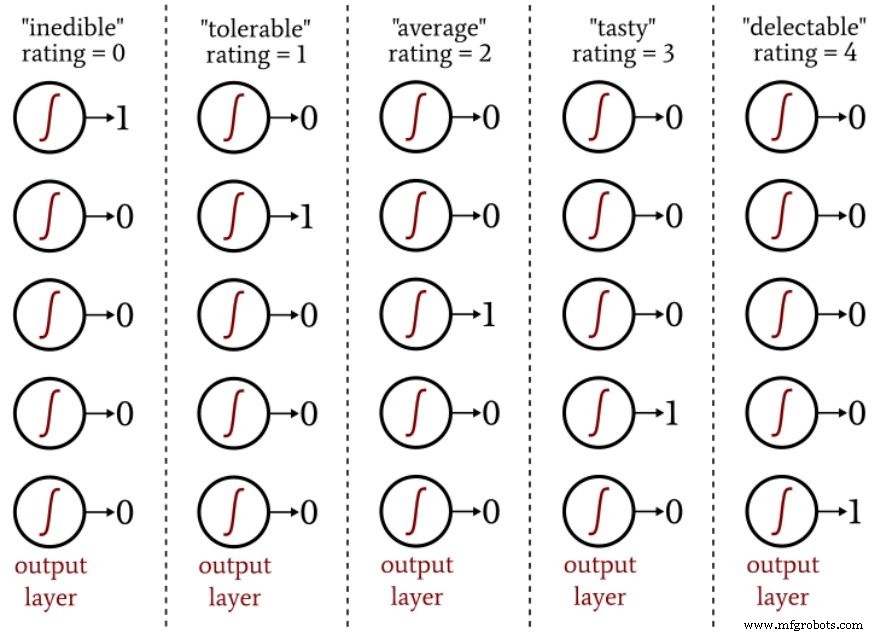
Le schéma de sortie unique nous permet de quantifier les classifications non binaires d'une manière compatible avec l'activation logistique-sigmoïde. La sortie de la fonction logistique est essentiellement binaire car la zone de transition de la courbe est étroite par rapport à la plage infinie de valeurs d'entrée pour laquelle la valeur de sortie est très proche du minimum ou du maximum :

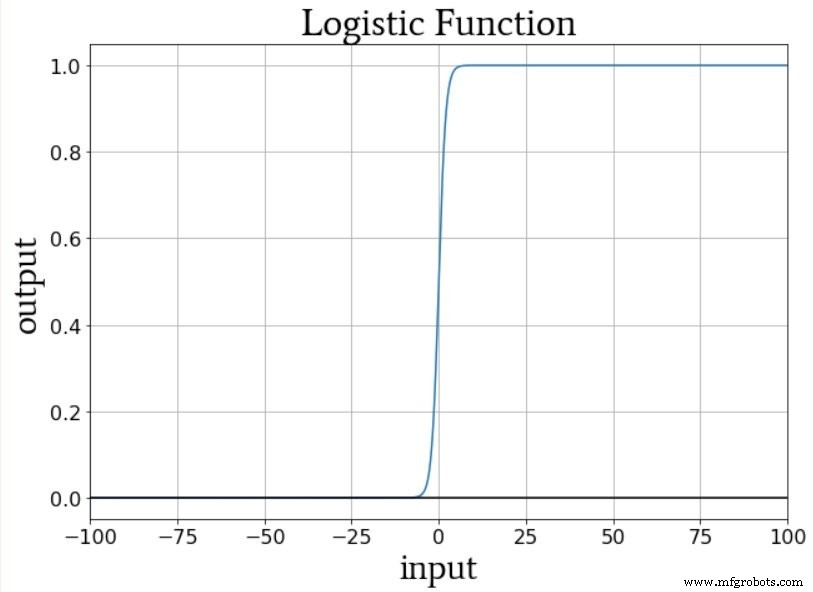
Ainsi, nous ne voulons pas configurer ce réseau avec un seul nœud de sortie, puis fournir des échantillons d'apprentissage qui ont des valeurs de sortie de 0, 1, 2, 3 ou 4 (ce serait 0, 0,2, 0,4, 0,6 ou 0,8 si vous souhaitez rester dans la plage 0 à 1 ); la fonction d'activation logistique du nœud de sortie favoriserait fortement les notes minimales et maximales.

Le réseau de neurones ne comprend tout simplement pas à quel point il serait absurde de conclure que toutes les tomates sont soit immangeables, soit délicieuses.

Création d'un ensemble de données d'entraînement

Le réseau de neurones Python dont nous avons parlé dans la partie 12 importe des échantillons d'apprentissage à partir d'un fichier Excel. Les données d'entraînement que je vais utiliser pour cet exemple sont organisées comme suit :

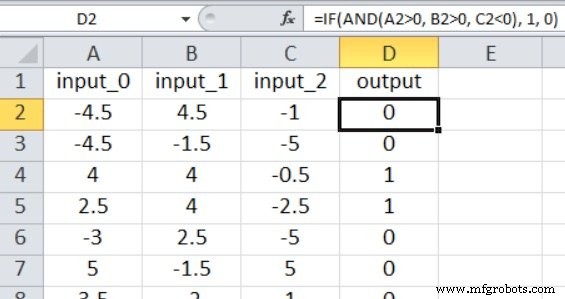
Notre code Perceptron actuel est limité à un nœud de sortie, donc tout ce que nous pouvons faire est d'effectuer un type de classification vrai/faux. Les valeurs d'entrée sont des nombres aléatoires entre –5 et +5, générés à l'aide de cette formule Excel :

=RANDBETWEEN(-10, 10)/2

Comme le montre la capture d'écran, la sortie est calculée comme suit :

=IF(AND(A2>0, B2>0, C2<0), 1, 0)

Ainsi, la sortie n'est vraie que si input_0 est supérieur à zéro, input_1 est supérieur à zéro et input_2 est inférieur à zéro. Sinon, c'est faux.

Il s'agit de la relation entrée-sortie mathématique que le Perceptron doit extraire des données d'apprentissage. Vous pouvez générer autant d'échantillons que vous le souhaitez. Pour un problème simple comme celui-ci, vous pouvez atteindre une précision de classification très élevée avec 5 000 échantillons et une époque.

Former le réseau

Vous devrez définir votre dimensionnalité d'entrée sur trois (I_dim =3, si vous utilisez mes noms de variables). J'ai configuré le réseau pour avoir quatre nœuds cachés (H_dim =4), et j'ai choisi un taux d'apprentissage de 0,1 (LR =0,1).

Trouvez les training_data =pandas.read_excel(...) déclaration et insérez le nom de votre feuille de calcul. (Si vous n'avez pas accès à Excel, la bibliothèque Pandas peut également lire les fichiers ODS.) Cliquez ensuite simplement sur le bouton Exécuter. L'entraînement avec 5 000 échantillons ne prend que quelques secondes sur mon ordinateur portable Windows 2,5 GHz.

Si vous utilisez le programme complet "MLP_v1.py" que j'ai inclus dans la partie 12, la validation (voir la section suivante) commence immédiatement après la fin de la formation, vous devrez donc préparer vos données de validation avant de former le réseau. .

Validation du réseau

Pour valider les performances du réseau, je crée une deuxième feuille de calcul et génère des valeurs d'entrée et de sortie en utilisant exactement les mêmes formules, puis j'importe ces données de validation de la même manière que j'importe des données d'entraînement :

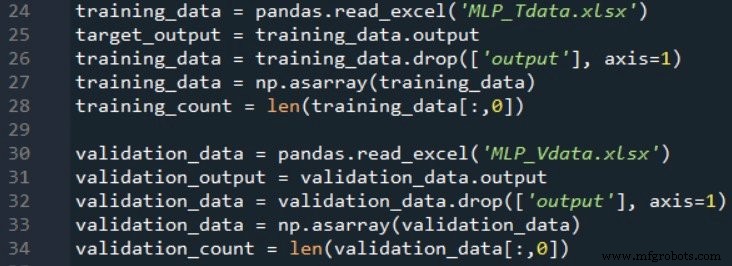
L'extrait de code suivant vous montre comment effectuer une validation de base :

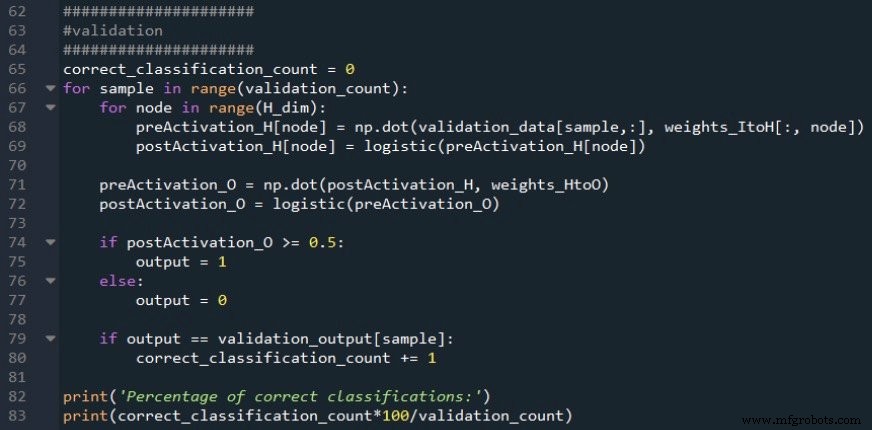
J'utilise la procédure d'anticipation standard pour calculer le signal de postactivation du nœud de sortie, puis j'utilise une instruction if/else pour appliquer un seuil qui convertit la valeur de postactivation en une valeur de classification vrai/faux.

La précision de la classification est calculée en comparant la valeur de classification à la valeur cible pour l'échantillon de validation actuel, en comptant le nombre de classifications correctes et en divisant par le nombre d'échantillons de validation.

N'oubliez pas que si vous avez le np.random.seed(1) instruction commentée, les poids s'initialiseront à différentes valeurs aléatoires à chaque fois que vous exécuterez le programme et, par conséquent, la précision de la classification changera d'une exécution à l'autre. J'ai effectué 15 analyses distinctes avec les paramètres spécifiés ci-dessus, 5 000 échantillons d'apprentissage et 1 000 échantillons de validation.

La précision de classification la plus faible était de 88,5 %, la plus élevée était de 98,1 % et la moyenne était de 94,4 %.

Conclusion

Nous avons couvert certaines informations théoriques importantes liées aux données d'entraînement des réseaux de neurones, et nous avons effectué une première expérience d'entraînement et de validation avec notre Perceptron multicouche en langage Python. J'espère que vous appréciez la série d'AAC sur les réseaux de neurones. Nous avons fait beaucoup de progrès depuis le premier article, et il nous reste encore beaucoup à discuter !