Simplification de la logique avec Karnaugh Maps

Les exemples de simplification logique que nous avons faits jusqu'à présent auraient pu être exécutés avec l'algèbre booléenne à peu près aussi rapidement. Les problèmes de simplification de la logique du monde réel nécessitent des cartes de Karnaugh plus grandes afin que nous puissions faire un travail sérieux.

Nous allons travailler quelques exemples artificiels dans cette section, laissant la plupart des applications du monde réel pour le chapitre Logique combinatoire. Par artificiel, nous entendons des exemples qui illustrent des techniques.

Cette approche développera les outils dont nous avons besoin pour passer aux applications plus complexes du chapitre Logique combinatoire.

Carnes de Karnaugh et séquence de codes Gray

Nous montrons notre carte de Karnaugh développée précédemment. Nous utiliserons le formulaire à droite.

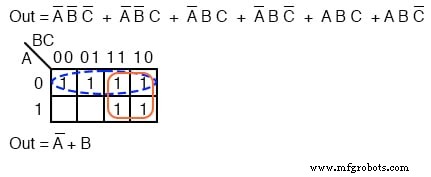
Notez la séquence de chiffres en haut de la carte. Ce n'est pas dans une séquence binaire qui serait 00, 01, 10, 11 . Il est 00, 01, 11 10 , qui est la séquence de code Gray. La séquence de code Gray ne change qu'un bit binaire lorsque nous passons d'un nombre à l'autre dans la séquence, contrairement au binaire.

Cela signifie que les cellules adjacentes ne varieront que d'un bit, ou variable booléenne. C'est ce dont nous avons besoin pour organiser les sorties d'une fonction logique afin que nous puissions voir les points communs.

De plus, les en-têtes des colonnes et des lignes doivent être dans l'ordre du code Gray, sinon la carte ne fonctionnera pas comme une carte de Karnaugh. Les cellules partageant des variables booléennes communes ne seraient plus adjacentes et n'afficheraient plus de modèles visuels.

Les cellules adjacentes ne varient que d'un bit car une séquence de code Gray ne varie que d'un bit.

Génération du code Gray

Si nous dessinons nos propres cartes de Karnaugh, nous devons générer du code Gray pour toutes les tailles de carte que nous pouvons utiliser. C'est ainsi que nous générons du code Gray de toute taille.

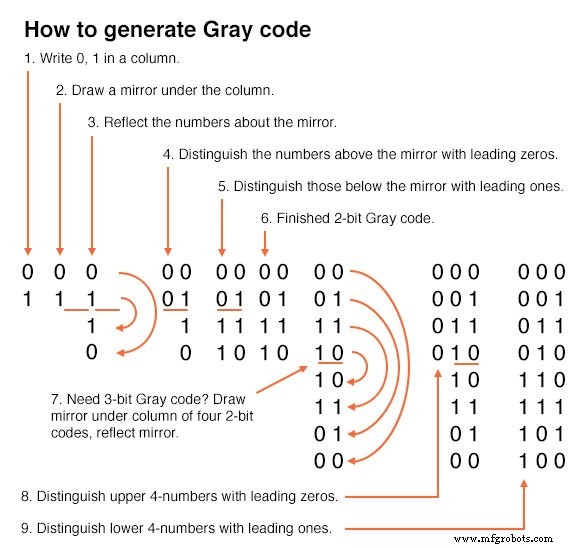
Notez que la séquence du code Gray, en haut à droite, ne varie que d'un bit au fur et à mesure que nous descendons dans la liste, ou en bas pour remonter la liste. Cette propriété du code Gray est souvent utile pour l'électronique numérique en général. En particulier, cela s'applique aux cartes de Karnaugh.

Exemples de simplification avec Karnaugh Maps

Passons à quelques exemples de simplification avec des cartes de Karnaugh à 3 variables. Nous montrons comment mapper les termes de produit de la logique non simplifiée à la K-map.

Nous illustrons comment identifier des groupes de cellules adjacentes, ce qui conduit à une simplification de la somme des produits de la logique numérique.

Au-dessus de nous, placez les 1 dans la K-map pour chacun des termes du produit, identifiez un groupe de deux, puis écrivez un p-term (terme de produit) pour le groupe unique comme résultat simplifié.

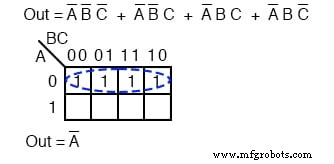
La cartographie des quatre termes de produit ci-dessus donne un groupe de quatre couverts par le booléen A’

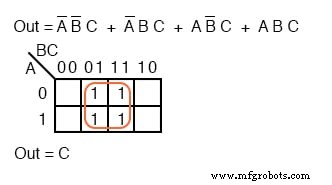
La cartographie des quatre p-termes donne un groupe de quatre, qui est couvert par une variable C .

Après avoir cartographié les six p-termes ci-dessus, identifiez le groupe supérieur de quatre, sélectionnez les deux cellules inférieures en tant que groupe de quatre en partageant les deux avec deux autres de l'autre groupe. Couvrir ces deux avec un groupe de quatre donne un résultat plus simple.

Puisqu'il y a deux groupes, il y aura deux p-termes dans le résultat de la somme des produits A'+B

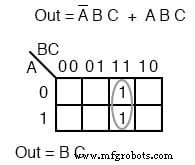
Les deux termes de produit ci-dessus forment un groupe de deux et se simplifient en BC

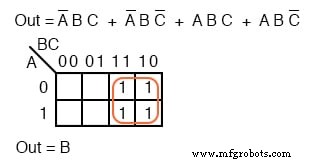
La cartographie des quatre p-termes donne un seul groupe de quatre, qui est B

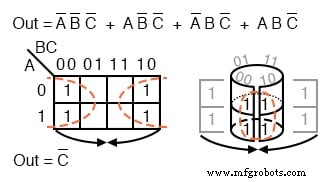
La cartographie des quatre p-termes ci-dessus donne un groupe de quatre. Visualisez le groupe de quatre en enroulant les extrémités de la carte pour former un cylindre, puis les cellules sont adjacentes. Nous marquons normalement le groupe de quatre comme ci-dessus à gauche.

Parmi les variables A, B, C, il existe une variable commune :C'. C' est un 0 dans l'ensemble de quatre cellules. Le résultat final est C'

.

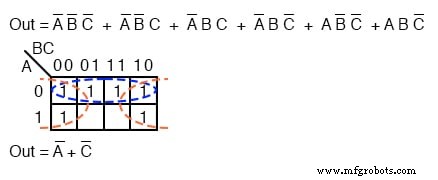
Les six cellules ci-dessus de l'équation non simplifiée peuvent être organisées en deux groupes de quatre. Ces deux groupes devraient nous donner deux p-termes dans notre résultat simplifié de A’ + C’ .

Simplification des équations booléennes avec Karnaugh Maps

Ci-dessous, nous revisitons l'incinérateur de déchets toxiques du chapitre sur l'algèbre booléenne. Voir le chapitre sur l'algèbre booléenne pour plus de détails sur cet exemple. Nous allons simplifier la logique en utilisant une carte de Karnaugh.

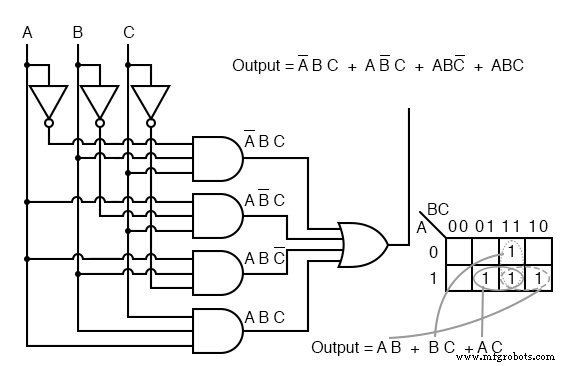
L'équation booléenne pour la sortie a quatre termes de produit. Tracez quatre 1 correspondant aux p-termes. Formant des groupes de cellules, nous avons trois groupes de deux. Il y aura trois p-termes dans le résultat simplifié, un pour chaque groupe. Voir Convertir des tables de vérité en expressions booléennes du chapitre 7 pour un diagramme de porte du résultat, qui est reproduit ci-dessous.

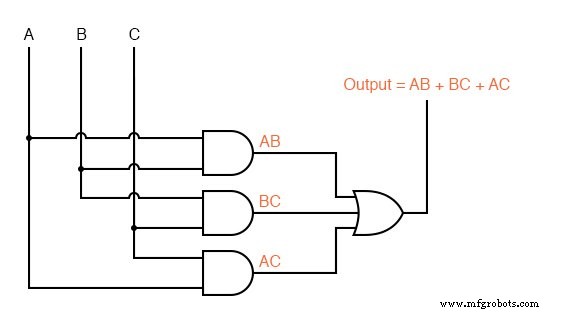
Ci-dessous, nous répétons la simplification de l'algèbre booléenne de l'incinérateur de déchets toxiques à des fins de comparaison.

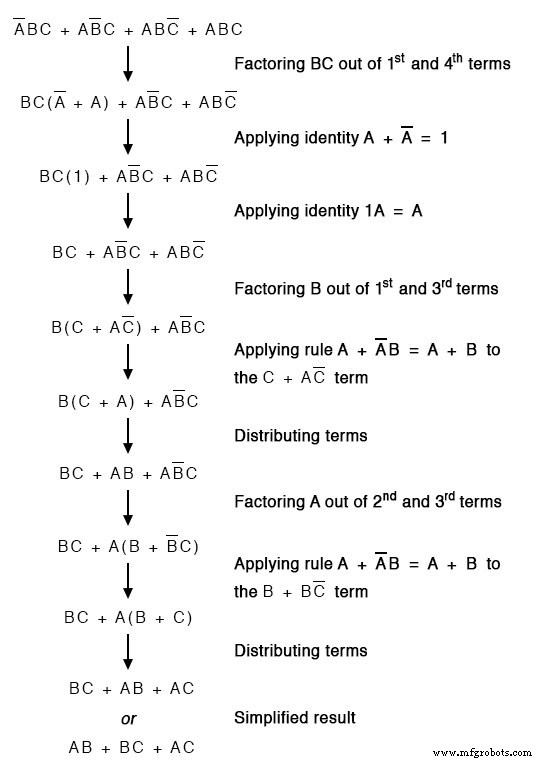
Ci-dessous, nous répétons la solution cartographique de l'incinérateur de déchets toxiques de Karnaugh à des fins de comparaison avec la simplification de l'algèbre booléenne ci-dessus. Ce cas illustre pourquoi la carte de Karnaugh est largement utilisée pour la simplification logique.

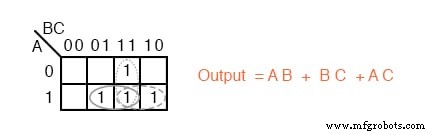
La méthode de la carte de Karnaugh semble certainement plus simple que les pages précédentes de l'algèbre booléenne.

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail de cartographie de Karnaugh