Formules mathématiques magiques pour les nanoboîtes

Résumé

Les nanostructures creuses sont à la pointe de nombreux efforts scientifiques. Ceux-ci se composent de nanoboîtes, de nanocages, de nanocadres et de nanotubes. Nous examinons les mathématiques de la coordination atomique dans des nanoboîtes. De telles structures consistent en une boîte creuse avec n coquillages et t les couches externes. Les formules magiques que nous dérivons dépendent à la fois de n et t . Nous constatons que les nanobox avec t = 2 ou 3, ou les murs avec seulement quelques couches ont généralement des atomes coordonnés en vrac. Les avantages d'une faible coordination dans les nanostructures ne se produisent que lorsque l'épaisseur de la paroi est beaucoup plus fine que celle normalement synthétisée. Le cas où t = 1 est unique et possède des formules magiques distinctes. Ces nanoboîtes faiblement coordonnées présentent un intérêt pour une myriade d'applications, notamment les batteries, les piles à combustible, les utilisations plasmoniques, catalytiques et biomédicales. Compte tenu de ces formules, il est possible de déterminer la dispersion surfacique des nanoboîtes. Nous nous attendons à ce que ces formules soient utiles pour comprendre comment la coordination atomique varie avec n et t dans une nanobox.

Introduction

Les nanoboîtes ont été synthétisées à l'origine vers 2002 [1, 2]. Une nanoboîte se distingue d'une nanocage en ce que cette dernière a des parois poreuses. En outre, les deux sont distincts d'un nanoframe, en ce que le nanoframe est une structure (frame) constituée du contour faiblement coordonné du cluster. De telles structures polyédriques anisotropes peuvent être créées à partir de réactions de déplacement galvanique [3, 4]

$$\begin{array}{l}\\ {\hbox{Anode}} :yA_{(s)}\rightarrow yA_{({{\rm aq}})}}^{x+}+xye_{({{ \rm aq}})}^{-} \\ {\hbox{Cathode}} :xB_{({{\rm aq}})}^{y+} + xye_{({{\rm aq}})} ^{-} \rightarrow xB_{(s)} \\ {\hbox{Complet\,Réaction}} :yA_{(s)}+xB_{({{\rm aq}})}^{y+} \rightarrow yA_{({{\rm aq}})}^{x+}+xB_{(s)} \\ \end{array}$$ (1)

où un nanocluster avec du métal A est creusé de manière sacrificielle par une solution aqueuse de métal B , qui a un potentiel de réduction plus élevé et crée le solide creux de l'élément B . Des demi-réactions se produisent à l'anode et à la cathode d'une cellule électrochimique, entraînant la réaction combinée complète comme ci-dessus [5]. Dans certains cas, les scientifiques ont combiné le déplacement galvanique avec la formation de vide via la diffusion Kirkendall Fickian des métaux et des lacunes [6]. Des modèles pour cette activité existent pour des cas spécifiques et des expériences de microscopie électronique in situ ont été rapportées [7, 8]. D'autres méthodes de synthèse incluent la gravure chimique [9], l'échange d'ions [10] et les structures métal-organiques (MOF) [11, 12]. Un examen récent des méthodes de synthèse mentionne que des amas anisotropes n'ont pas encore été formés dans la région de taille \(2

De telles structures creuses ont une faible coordination, ce qui les rend intéressantes pour les batteries [12], les piles à combustible [14], les applications plasmoniques [15], catalytiques [16] et biomédicales [17]. Une analyse précédente montre que pour les applications catalytiques, une approche de coordination s'applique [18], tandis que pour le stockage d'énergie, il n'y a que quelques indices avec les résultats de la théorie fonctionnelle de la densité (DFT) indiquant que certaines facettes sont importantes [19]. Nous utilisons une méthode précédemment dérivée de l'analyse matricielle d'adjacence [20, 21] pour découvrir la coordination atomique d'une boîte avec n coques et une épaisseur de paroi de t couches. Cette analyse montre qu'une nanobox avec t = 2 ou 3 a une coordination en vrac et, en tant que tel, les avantages d'une faible coordination ne sont présents que pour les nanoboîtes avec des parois plus minces que ce que l'on croit généralement nécessaire. Les méthodes que nous utilisons quantifient la coordination atomique à l'aide de nombres magiques et de formules pour treize types de nanoboîtes.

Méthodes

La clé de notre analyse par des méthodes de coordination, est la création d'une matrice d'adjacence à partir des coordonnées atomiques de la nanobox. Une telle matrice est créée comme suit. Nous définissons i et j comme voisins les plus proches, et les séparer du reste en exigeant que la longueur de liaison \(r_{ij} $${\mathbf{A}}(i,j)=\left\{ \begin{array}{ll} 1 &{\quad}\hbox { if } r_{ij} décrit la matrice d'adjacence pour le cluster, et

$${\mathbf{E}}(i,j)=\left\{ \begin{array}{ll} r_{ij} &{\quad}\hbox { if } \, r_{ij} décrit la matrice euclidienne de la boîte. Nous utilisons la matrice euclidienne pour déterminer le diamètre, D , (nm) pour les nanoboîtes.

Puisque nous créons des matrices d'adjacence des voisins les plus proches, nous connaissons le numéro de coordination $\hbox {cn}_i$ du sommet i en additionnant les éléments de ${{\mathbf{A}}}(i,:)$. Notre structure est constituée de $n+1$ coques numérotées 0, 1, ..., n , avec t les couches externes. Soit $N_{{\rm cn}_i}(n,t)$ le nombre d'atomes de coordination $\hbox {cn}_i$ où $1\le \hbox{cn}_i\le \hbox{cn}_M$ avec $\hbox {cn}_M$ la coordination maximale dans la nanobox. Ensuite, le nombre total d'atomes dans la nanobox est donné par

$$N_T(n,t) =\sum _{{\rm cn}_i=1}^{{\rm cn}_M}{N_{{\rm cn}_i}(n,t)}.$$ (4)

Les atomes de surface dans l'enveloppe extérieure (ou intérieure) de la nanoboîte, n avoir un ensemble de liaisons inférieur à la coordination en vrac. Ainsi la coordination maximale pour les atomes de surface est $\hbox {cn}_s <\hbox{cn}_M$, et le nombre d'atomes de surface est

$$N_S(n,t) =\sum _{{\rm cn}_i=1}^{{\rm cn}_s}{N_{{\rm cn}_i}(n,t)}.$$ (5)

Ceci est valable si tous les sommets non surfaciques ont une coordination supérieure à $\hbox {cn}_s$, ce qui est vrai pour tous les clusters fcc, bcc et hcp. On détermine le $N_{{\rm cn}_i}(n,t)$ en comptant les colonnes de la matrice d'adjacence dont la somme est $\hbox {cn}_i$. Notez que notre algorithme de coordonnées de cluster est construit par des coques, de sorte que chaque coque suivante contient toutes les valeurs inférieures précédentes de n . De plus, le nombre de liens dans la boîte est

$$N_{{\rm B}}(n,t) =\frac{1}{2}\sum _{{\rm cn}_i=1}^{{\rm cn}_M}{\hbox{ cn}_i\cdot N_{{\rm cn}_i}(n,t)},$$ (6)

où $N_{{\rm B}}(n,t)$ est le nombre de liaisons et $\hbox {cn}_M$ est la coordination maximale. Le facteur 1/2 est dû à la liaison du voisin le plus proche par paire.

Puisque nous savons que ces équations dépendent de n , t comme polynôme de degré au plus 3, on peut calculer $N_{{\rm cn}_i}(n,t)$ pour 4 valeurs consécutives de n , dites $n=n_0+j$, j =0, 1, 2, 3. Un simple polynôme d'interpolation donnera alors les coefficients du polynôme. Il faut vérifier qu'en augmentant $n_0$, qui est généralement égal à 1, les formules ne changent pas. Si les formules deviennent stables à partir de $n_0$, alors elles sont valables pour tout $n\ge n_0$. Pour obtenir les coefficients rationnels exacts, il faut résoudre le système de Vandermonde pour les coefficients en arithmétique exacte.

Notez que dans les formules magiques pour les nanoboîtes nous avons que $n> t$ donc contrairement à toute attente, remplir la boîte par un choix approprié de t ne recréera pas les formules magiques originales pour les grappes solides complètes. Ces formules magiques sont utiles pour modéliser les propriétés à mésoéchelle des clusters et des boîtes, ou cages. Des ensembles complets de formules ont été dérivés à l'origine pour dix-neuf types de clusters. Dans ce manuscrit, nous dérivons des formules magiques pour treize types de nanoboîtes.

Dans les formules magiques ci-dessous, nous constatons qu'une coordination en vrac peut apparaître pour t = 2 ou t = 3 couches d'épaisseur de coque. La plupart sont pour les calques où t = 2 ; les exceptions sont le cube fcc, le cuboctaèdre, l'icosaèdre et le cube bcc et le cube tronqué. Dans ce dernier cas, la coordination en masse n'apparaît que pour t = 3 couches. Pour les données ci-dessous, les tableaux des formules magiques sont accompagnés d'une figure de « demi-boîte » pour montrer l'intérieur des nanoboîtes. À côté se trouve une barre de couleur indiquant la coordination et le nombre de ces éléments entre parenthèses.

Résultats et discussion

Afin de délimiter l'applicabilité des formules magiques, nous décrivons comment le comportement catalytique peut dépendre de la coordination et de ces formules. Nous définissons G comme l'énergie de Gibbs dépendant de la taille de l'amas. En raison des adatomes liés aux atomes de la couche externe, il y a une augmentation de G c'est ce qu'on appelle l'énergie d'adsorption et est noté $\Delta G$. Cela peut être divisé en différents types de coordination des atomes sur la couche externe se liant aux adatomes. Par exemple, un atome coudé ajoute à l'énergie d'adsorption une quantité $\Delta G_{k}$. De même un atome de bord ajoute $\Delta G_{e}$, tandis qu'un atome de facette contribue $\Delta G_f$ puis [18] :

$$\Delta G=\sum _{o\in \{f,e,k\}} \Delta G_o N_o$$ (7)

où $N_o$ est le nombre d'atomes dans la couche externe du type indiqué. Le nombre total d'atomes dans l'enveloppe externe liés aux adatomes est défini comme $N_s=N_f+N_e+N_k$, ce qui donne :

$$\begin{aligned}\Delta G=&{} \Delta G_f\cdot (1-f_e-f_k)+\Delta G_e\cdot f_e+\Delta G_k\cdot f_k \\&\quad {\hbox{where} } \,\,f_o=N_o/N_s, \,\,o\in \{e,k\},\end{aligned}$$ (8)

avec la fraction d'énergie de Gibbs exprimée à travers les sites de bord et de pli qui ont des coordinations explicites pour des structures spécifiques. Cela démontre que les formules magiques ont un rôle dans les réactions de surface, à travers les coordinations de bords et de plis et leurs formules. Notez que l'équation. (8) s'applique à l'adsorption sur les sites supérieurs, sinon tous les adatomes ne seront pas liés aux atomes de l'enveloppe externe. Dans un tel modèle, les sites kink ont des formules magiques qui sont constantes avec le nombre de coquilles, n , les sites périphériques ont des formules linéaires avec n , et les sites de facettes ont des formules quadratiques avec n . Plus précisément, les sites kink sont les formules coordonnées les plus faibles, les sites périphériques sont les deuxièmes coordonnées les plus faibles et les sites de facettes ont cn = 8 pour (100) facettes et cn = 9 pour (111) facettes.

Deux relations fondamentales par particule peuvent être appliquées. Pour l'énergie de Gibbs et la constante d'adsorption, $K_{{\rm a}}$, elle est vérifiée :

$$K_{{\rm a}}={\exp } \left( -\frac{\Delta G}{RT}\right) ,$$ (9)

où R est la constante des gaz et T est la température en Kelvin. De plus, les relations de Brønsted-Evans-Polanyi sont largement utilisées en catalyse homogène et hétérogène [18, 22] en utilisant une relation pour les constantes de réaction k et constantes d'équilibre K comme suit :

$$k=gK^{\alpha },\quad 0<\alpha <1,$$ (10)

où g et $\alpha$ (paramètre Polanyi) sont des constantes. Le paramètre de Polanyi est sans unité et une fraction appropriée, comme donné à l'origine par Brønsted [23]. On a alors :

$$k=k'_{a}{\exp } \Bigl (-\alpha \bigl ({f_n^{e}\cdot \chi _{_e}({D_n}) +f_n^{k}\cdot \chi _{_k}({D_n})}\bigr )\Bigr ),$$ (11)

où

$$\begin{aligned} &\chi _{_e}(D)=\frac{\Delta G_e(D)-\Delta G_f(D)}{RT},\\&\chi _{_k}(D )=\frac{\Delta G_k(D)-\Delta G_f(D)}{RT}, \end{aligné}$$ (12)

$$k'_{a}=g\exp \left( -\alpha \frac{\Delta G_f}{RT}\right) .$$ (13)

Cette analyse montre que la détermination d'un modèle catalytique nécessite une méthode de calcul de l'énergie de Gibbs. Des réactions catalytiques connues telles que les mécanismes en deux étapes et de Langmuir-Hinshelwood ont été prises en compte [24].

Nanobox FCC

Les structures cubiques à faces centrées sont la forme la plus courante pour les nanoclusters et les nanoboxes. C'est la structure des métaux aux propriétés intéressantes, comme les métaux nobles aux propriétés plasmoniques, et les métaux précieux catalytiques. Étant donné que l'or a un potentiel de réduction élevé de 1,50 V (voir l'équation 1) par rapport à l'électrode à hydrogène standard (SHE) [5], c'est l'un des métaux les plus faciles à synthétiser sous forme de nanoboîte ou de nanocage. Des nanoboîtes ou nanocages en or ont été formées sous des formes cubique [1], cuboctaèdre [25], icosaèdre et décaèdre [26], octaèdre [27] et tétraèdre [28].

Nous pouvons déterminer la taille approximative de ces nanoboîtes en utilisant une approche de coordination pour la longueur de liaison du voisin le plus proche r (cn) [29],

$$r(cn) =\frac{2r_{{\rm B}}}{\left( 1+\exp \left( \frac{12 - \langle cn \rangle _c)}{8\cdot \langle cn \rangle _c}\right) \right) }.$$ (14)

Ici $r_{{\rm B}}$ est la longueur de liaison en vrac pour l'or (0,2884 nm) et $\langle cn \rangle _c$ est la coordination moyenne du cluster. Nous trouvons une relation linéaire entre D et n , le nombre de shells de cluster, comme indiqué dans le tableau 1 :

$$D(n)=a \cdot r_{{\rm B}} \cdot n + b.$$ (15)

Nous utilisons des nanobox avec t = 3, car les formules varient avec t , et nous souhaitons réaliser une certaine coordination en bloc. Pour le calcul de D (n ), nous utilisons la distance maximale entre les atomes de l'amas, dérivée de la matrice euclidienne. Notez que D (n ) est une formule empirique, dérivée de données (variez n et calculez D ), et en tant que tel n'est pas prouvé.

Ces relations produisent des diamètres en accord avec d'autres données, de DFT. Pour les cuboctaèdres solides avec N égal à 55, 561 et 923, nous obtenons des diamètres de 1,12 nm, 2,85 nm et 3,43 nm. Cela se compare favorablement aux résultats DFT publiés pour 55 atomes de 1,1 nm [30], pour 561 atomes, 2,7 nm [31] et pour 923 atomes, 3,5 nm [30]. Les formules magiques de certaines nanoboxes fcc sont présentées ci-dessous (tableaux 2, 3, 4, 5, 6, 7, 8).

Nanoboxes icosaédriques et décaédriques

Voir les tableaux 9 et 10.

Diamond and Simple Cubic Nanoboxes

La structure en réseau cubique du diamant est formée d'un allotrope de carbone ainsi que des éléments silicium et germanium. En outre, certains composés cubiques forment cette structure, comme l'oxyde de fer cubique, la maghémite de diamant tétraédrique $\gamma$-Fe₂ O₃ . La longueur de liaison pour Fe–O dans la maghémite diamant tétraédrique $\gamma$-Fe₂ O₃ = 0,186 nm [32]. Cela conduit au diamètre des grappes de diamants D (n ) comme ci-dessous :

$$D(n) =3,3984\cdot n_{{\rm B}} \cdot n - 0,21194.$$ (16)

Selon la référence [12], des microboîtes d'oxyde de fer cubique se sont formées et avaient des capacités de stockage de lithium intéressantes. Nous ne connaissons pas de modèle de coordination complet pour le stockage d'énergie, mais comme mentionné ci-dessus, les résultats DFT indiquent que l'activité peut dépendre de l'orientation des facettes [19]. Aucun modèle de dépendance de stockage sur la coordination n'existe actuellement comme nous l'avons pour la catalyse. À partir de l'équation (16) ci-dessus (créée à l'aide de t = 4), une microbox nécessite environ n = 1600 obus pour diamant maghémite. Les formules magiques pour les structures en losange et en réseau cubique simple sont répertoriées ci-dessous (tableaux 11, 12).

Nanoboxes BCC

Voir les tableaux 13, 14 et 15.

Nanobox HCP

Voir le tableau 16.

Le cas t = 1

Le cas particulier t = 1 est unique et, en tant que tel, a des formules magiques distinctes. Nous examinons ce cas pour certaines des nanoboîtes ci-dessus. Des nanoboîtes à parois ultrafines ont été formées avec des formes cubiques [33], octaédriques [16] et icosaédriques [34]. D'après les formules magiques ci-dessous, la nanobox cubique avec t = 1 a la coordination la plus faible. Le platine a un potentiel de réduction relativement élevé de 1,18 V par rapport au SHE, il peut donc être formé par remplacement galvanique, voir Eq. (1) [5]. Cependant, les propriétés de réaction d'oxydoréduction (ORR) de certaines de ces nanocages à base de platine indiquent que les structures avec (111) facettes par opposition à (100) facettes ont de meilleures activités de masse ORR [35].

Ainsi l'icosaèdre à 20 (111) facettes a la meilleure activité de masse ORR, suivi de l'octaèdre, et enfin du cube tronqué. Cette propriété de comportement catalytique de l'orientation des facettes prenant le pas sur le nombre de coordination est mise en évidence par les données tabulaires ci-dessous. En d'autres termes, comme mentionné dans les tableaux suivants, le cube avec (100) facettes a les nombres de coordination magique les plus bas avec quatre et cinq, mais l'octaèdre et l'icosaèdre avec (111) facettes et les formules magiques plus grandes ont une meilleure activité ORR. Cette propriété est également mise en évidence dans les nanoclusters, où les résultats DFT confirment la dominance des (111) facettes [36], en particulier pour les alliages PtNi (tableaux 17, 18, 19, 20, 21).

Dispersion

Compte tenu de l'importance des sites de bord et de pliage par rapport à ceux des facettes en ce qui concerne l'activité catalytique, nous avons déterminé la dispersion de surface pour certaines des nanoboîtes que nous étudions. Les (100) facettes ont cn = 8 tandis que les (111) facettes ont cn = 9. Cela peut donner un aperçu des raisons de l'activité polyédrique individuelle par rapport aux nanoboîtes. Dans la figure 1 ci-dessous, nous traçons la dispersion de surface $D_{{\rm s}} =(N_{{\rm e}} + N_{{\rm k}}) / N_{{\rm S}} \cdot 100\%$. Dans cette relation $N_{{\rm k}}$ est le nombre de sites de pli ou de coin et $N_{{\rm e}}$ le nombre de sites de bord. Comme on peut le voir sur la figure 1, les nanoboîtes avec des surfaces (111) par opposition aux surfaces (100) ont une dispersion plus élevée, ce qui donne du crédit à la préférence de l'activité catalytique de la facette (111).

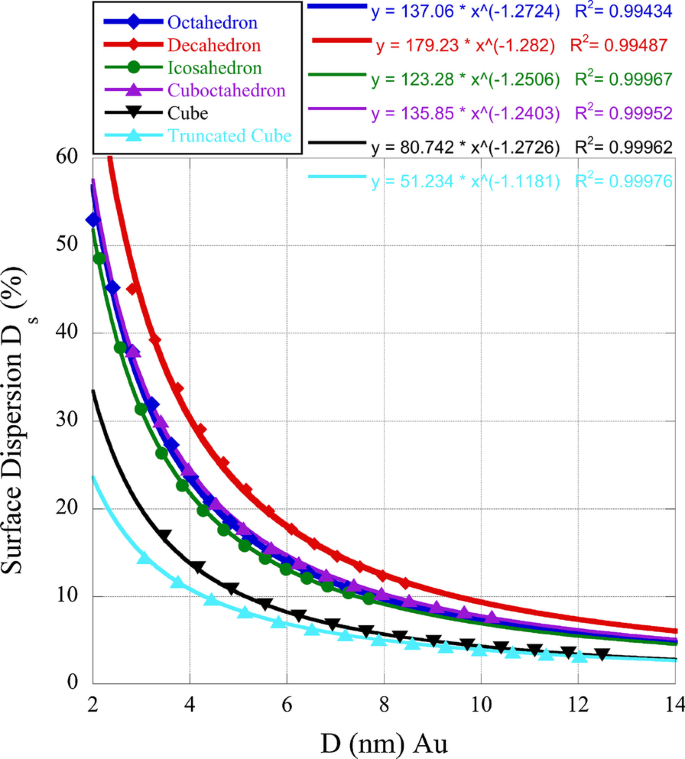
Dispersion en surface des nanoboîtes d'or

Conclusion

En résumé, nous avons présenté la première description mathématique détaillée des formules magiques pour les nanoboîtes. Le cas de l'épaisseur de coque, t = 1 est distinct de $t>1$ et nous tabulons les données pour certains de ces cas. Les formules pour la coordination, le nombre d'atomes et le nombre de liaisons sont toutes énumérées. Nous constatons que la coordination en vrac apparaît pour les couches où t = 2 ou 3, et en tant que tel est beaucoup plus mince que normalement synthétisé. Les avantages d'une faible coordination ne sont obtenus que pour des parois très minces. Nous nous attendons à ce que ces résultats soient utiles pour la modélisation et les travaux expérimentaux.

Disponibilité des données et des matériaux

Le ou les ensembles de données étayant les conclusions de cet article peuvent être obtenus auprès de l'auteur correspondant.

Abréviations

cci :: Corps cubique centré
fcc :: Cubique face centrée
hcp :: Hexagonal fermé emballé
DFT :: Théorie fonctionnelle de la densité
ELLE :: Electrode secondaire à hydrogène

Évaluation quantitative de l'internalisation cellulaire de nanoparticules polymères dans les cellules cancéreuses du larynx et les cellules immunitaires pour une administration améliorée des méd… Un photodétecteur double à quatre quadrants basé sur du silicium noir nanométrique amélioré dans le proche infrarouge

Nanomatériaux