Relations mathématiques magiques pour les nanoclusters

Introduction

Les nombres magiques et les formules pour les nanoclusters ont une longue histoire qui remonte à la publication prémonitoire de van Hardeveld et Hartog en 1969 [1]. Leurs idées sont antérieures à l'ère des nanosciences. Depuis lors, nous avons vu apparaître des nombres magiques dans des polygones 2D et des polyèdres 3D [2], des fullerènes de carbone [3], et dans une portée limitée à nouveau dans des clusters [4]. Des matériaux aussi divers que le silicium [5], le bore [6], et en fait plus de 1000 publications du service d'indexation « Web of Science » font référence aux nombres magiques dans les clusters. L'étude de la taille et de la forme des nanoclusters est importante pour la société d'aujourd'hui, car cela détermine non seulement les propriétés physiques et chimiques intrinsèques, mais aussi la pertinence pour les applications optiques, catalytiques, électroniques et magnétiques [7]. Notre objectif est de mettre à jour la base de données de ces connaissances avec les relations et les données actuelles, maintenant que nous sommes entrés dans le domaine nano.

L'apparition de nombres magiques dans les nanoclusters est principalement liée à la formation de couches d'atomes sur une cellule fondamentale. Lorsque le nombre d'atomes complète une coquille complète, nous trouvons un ensemble unique de nombres, appelé «magie», qui définit les coquilles d'atomes. Un cluster est représenté par un graphique avec les atomes comme sommets et les liaisons comme arêtes. Il se compose de coquilles imbriquées comme des couches d'oignon. Nous définissons les nombres de couches comme n et découvrez les relations mathématiques des nombres de coordination des voisins les plus proches, des liaisons, du nombre total d'atomes et de certains indices topologiques en fonction de n . L'article original de van Hardeveld et Hartog [1] considérait les clusters fcc, bcc et hcp. La référence de Teo et Sloane [2] considère les polyèdres et les solides platoniciens mais néglige la relation des numéros de coordination des voisins les plus proches. Nous ajoutons à cette base de données en examinant les solides cubiques simples, diamantés et platoniques, en plus des propriétés topologiques et de la dispersion des amas.

La transition de la taille de la masse aux grappes de quelques atomes concerne en réalité la relation entre les atomes de surface et les atomes de masse. Des propriétés telles que la chimie catalytique, la résonance plasmonique de surface et la photoluminescence optique à points quantiques [8] sont affectées par la coordination et le nombre d'atomes de surface. La dispersion ou le pourcentage relatif des atomes de surface est déterminé par le rapport des atomes de surface au nombre total d'atomes, comme cela a été considéré précédemment [9]. Notre analyse déterminera le classement relatif de la dispersion en termes de géométrie de cluster.

Les indices topologiques ont commencé avec l'article original de Wiener concernant son indice et les points d'ébullition de la paraffine [10]. Ce n'est que quelque temps plus tard que Hosoya a introduit un formalisme mathématique pour analyser les indices topologiques [11]. Nous avons précédemment introduit des indices topologiques et des nanoclusters [12]. A l'heure où nous écrivons ces lignes, il existe de nombreux indices dont certains dépendent de la matrice d'adjacence ou de distance. Nous montrons ici que dans de nombreuses formes de cluster, des relations mathématiques magiques existent pour les quatre indices en fonction de n et le nombre d'obus.

Méthodes

Pour chacun des types de clusters que nous étudions, nous créons un algorithme de calcul qui détermine les coordonnées atomiques des clusters. Nous procédons ensuite à la création d'une matrice d'adjacence et d'une matrice de distance définies comme suit. Une matrice d'adjacence A est créé là où nous définissons i et j comme voisins les plus proches et les séparer des autres en exigeant que r _ij <r _c , où r _c est une valeur seuil, légèrement au-dessus de la distance du voisin le plus proche, mais inférieure à la distance du deuxième voisin. Ainsi,

où r _ij est la distance euclidienne entre l'atome i et atome j . Une valeur appropriée pour r _c est de 1,32·r _min , où r _min est la plus petite longueur de liaison. Ceci s'applique à la structure dodécaédrique, ainsi qu'aux autres que nous étudions. Les numéros de coordination du cluster sont simplement le nombre d'éléments non nuls dans une colonne de la matrice d'adjacence. La matrice de distance est définie comme

$$ \mathbf{D}(i,j) =\left\{\begin{array}{ll} 0 &i =j \\ d_{ij} &i \neq j \end{array}\right. $$ (2)

où d _ij est la longueur du chemin le plus court dans le graphe à partir de i à j . Un algorithme efficace pour le calcul de la matrice de distance à partir de la matrice d'adjacence existe [13]. En utilisant ces définitions, nous pouvons calculer l'indice de Wiener, W (G ), l'indice hyper-Wiener, W W (G ), l'indice de Wiener inverse rW (G ), et l'indice de Szeged, Sz (G ), comme détaillé précédemment [14]. Ces calculs utilisent le même algorithme que nous avons utilisé précédemment pour les indices topologiques et les nanoclusters [12].

Les auteurs précédents ont proposé des preuves de relations magiques, que nous condensons dans notre notation, pertinentes pour le travail présenté ici [1, 2]. Puisque nous créons des matrices d'adjacence des voisins les plus proches, nous connaissons le nombre de coordination c n _i du sommet i en additionnant les éléments de A (i , :). Notre structure se compose de n +1 coquilles numérotées 0,1,…,n . Soit \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\) le nombre d'atomes de coordination c n _i où 1≤c n _i c n _M avec c n _M la coordination maximale dans le cluster. Ensuite, le nombre total d'atomes dans l'amas est donné par

$$ N_{T}(n) =\sum_{{cn}_{i}=1}^{{cn}_{M}}{N_{{cn}_{i}}(n)}. $$ (3)

Les atomes de surface dans l'enveloppe externe n avoir un ensemble de liaisons inférieur à la coordination en vrac. Ainsi, la coordination maximale pour les atomes de surface est c n _s <c n _M , et le nombre d'atomes de surface est

$$ N_{S}(n) =\sum_{{cn}_{i}=1}^{{cn}_{s}}{N_{{cn}_{i}}(n)}. $$ (4)

Ceci est valable si tous les sommets non surfaciques ont une coordination supérieure à c n _s , ce qui est vrai pour tous les clusters, mais notez l'écart pour le dodécaèdre ci-dessous. On détermine le \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\) en comptant les colonnes de la matrice d'adjacence dont la somme est c n _i . Notez que notre algorithme de coordonnées de cluster est construit par des coques, de sorte que chaque coque suivante contient toutes les valeurs inférieures précédentes de n . Dans la Fig. 1, nous illustrons les coques des clusters pour un cube fcc et un dodécaèdre. De plus, le nombre de liaisons dans le cluster est

$$ N_{B}(n) =\frac{1}{2}\sum_{{cn}_{i}=1}^{{cn}_{M}}{{cn}_{i}\ cdot N_{{cn}_{i}}(n)}, $$ (5)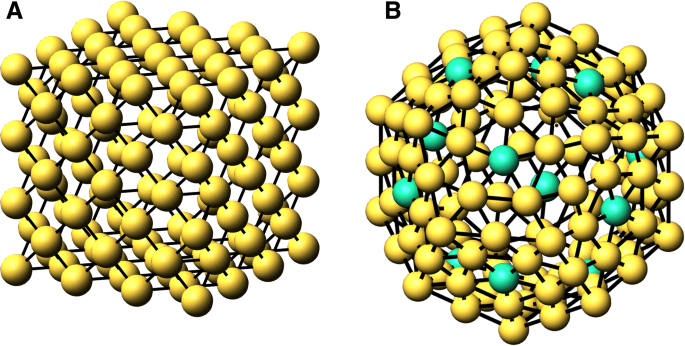

Coquilles d'atomes pour n =3 pour A. cube fcc et n =2 B. dodécaèdre. En B, les atomes verts (12) font référence à c n =5 dans le shell

où N _B (n ) est le nombre d'obligations et c n _M est la coordination maximale. Le facteur 1/2 est dû à la liaison par paires du voisin le plus proche. Cette relation magique ne semble pas avoir été prise en compte dans les publications précédentes, à l'exception de quelques clusters examinés dans [4]. Nous commentons également que Teo et Sloane ont dérivé le nombre total d'atomes, d'atomes de surface et d'atomes intérieurs pour les clusters comme suit [2] :

$$ N_{T}(n) =\alpha n^{3}+\frac{1}{2}\beta n^{2}+\gamma n+1~~n\ge{0} $$ ( 6)

où N _T (n ) est le nombre total d'atomes, et

$$ \alpha =C/6 $$ (7)

où C est le nombre de cellules tétraédriques en lesquelles le polyèdre est divisé, et

$$ \beta =1/2F_{s} $$ (8)

où F _s est le nombre de faces triangulaires sur la surface, et

$$ \gamma =F_{s}/4+V_{i}+1-C/6 $$ (9)

où V _i est le nombre de sommets à l'intérieur. Ils montrent également que

$$ N_{S}(n) =\beta n^{2}+2~~n\ge{1};~~N_{S}(0) =1 $$ (10)

et

$$ N_{I}(n) =N_{T}(n) - N_{S}(n), $$ (11)

où N _Je (n ) est le nombre d'atomes intérieurs. Cette information (Eq. (11)) est contenue dans la matrice d'adjacence, ainsi que les Eqs. (3, 4, 5). Ces équations sont une vérification des résultats des données de la matrice d'adjacence. Pour les polyèdres centrés, on a aussi

$$ N_{I}(n) =N_{T}(n-1), $$ (12)

et de l'éq. (11), nous avons

$$ N_{T}(n)=N_{S}(n)+N_{S}(n-1)+... +N_{S}(1)+N_{S}(0). $$ (13)

À partir de ces équations, nous pouvons dériver les formules magiques pour chacun des groupes comme suit. Après avoir calculé la matrice topologique (0,1)-adjacence A pour un cluster avec n coquilles comme décrit, nous savons que sa taille N =N _T (n ) indique le nombre total d'atomes. La somme des entrées dans la colonne i donne le nombre d'obligations c n _i (n ) pour l'atome i et en comptant le nombre de sommes de colonnes égales à c n _i (n ) donne évidemment \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\). Puisque nous savons que ceux-ci dépendent de n comme polynôme de degré au plus 3, on peut calculer N _T (n ) et c n _i (n ) pour 4 valeurs consécutives de n , dites n =n ₀ +j , j =0,1,2,3. Un simple polynôme d'interpolation donnera alors les coefficients polynomiaux. Il faut vérifier qu'en augmentant n ₀ , qui est généralement égal à 1, les formules ne changent pas. Si les formules deviennent stables à partir de n ₀ activé, puis ils sont valables pour tous les n n ₀ . Dans certains cas, la relation polynomiale n'est valable que pour le n pair valeurs ou impaires. Par exemple, pour le dodécaèdre rhombique fcc (tableau 1), les couches successives ont huit atomes de coordination 3 lorsque n ≥2 est pair, et aucun si n est impair. Dans de tels cas, différentes relations polynomiales seront valables pour n pair et n étrange, mais les données sont utilisées pour n =n ₀ +j , j =0,2,4,6 avec n ₀ impair (par exemple, n ₀ =1) ou n ₀ même (n ₀ =2). Pour obtenir les coefficients rationnels exacts, il faut résoudre le système de Vandermonde pour les coefficients en arithmétique exacte à l'aide de la boîte à outils symbolique de MATLAB. C'est ainsi que les tableaux 2, 3, 4, 5, 1, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 et 19 sont calculés. Dans la section suivante, nous déterminons les formules magiques pour N _T (n ), N _B (n ), et pour \(\phantom {\dot {i}\!}N_{{cn}_{i}}(n)\) selon la recette proscrite.

La dispersion (fraction exposée, FE) des atomes de surface est définie comme :

$$ \text{FE} =\frac{N_{S}}{N_{T}} \cdot 100\% $$ (14)

où N _S est le nombre d'atomes de surface, et N _T est le nombre total d'atomes [9]. Nous pouvons comparer des clusters dissemblables en définissant la taille relative du cluster comme :

$$ d_{rel} =b(N_{T})^{1/3};~~b =d_{at}^{-1}\cdot \left(\frac{6V_{u}}{\pi n_{u}}\right)^{1/3} $$ (15)

où d _à est le diamètre atomique covalent, V _u est le volume de la maille unitaire, et n _u est le nombre d'atomes dans la maille élémentaire. La constante de structure cristalline b est égal à 1,105 pour les clusters fcc et hcp, 1,137 pour les clusters bcc [1], 1,488 pour les clusters cubiques simples et 1,517 pour les clusters cubiques en diamant. Comme indiqué ci-dessus, la formule pour FE est un rapport d'un quadratique à un cubique pour les clusters et peut être modélisée par un ajustement de courbe de loi de puissance en fonction de d _rel . La variable d _rel nous permet de comparer différents amas les uns aux autres sans tenir compte de la structure cristalline. Pour certains des amas platoniciens, où il n'y a pas de maille cristalline, nous utilisons \(N_{T}^{1/3}\) comme variable.

Résultats et discussion

L'étude de la taille et de la forme des nanoclusters métalliques a évolué depuis ses débuts il y a deux décennies. Le tableau 20 montre certains progrès pertinents à partir de 2018.

Dans le tableau, nous répertorions principalement les métaux de transition, pas les alliages ou les composés, à l'exception de la bipyramide hexagonale tronquée, où seul Fe₂ O₃ a été trouvé. Il y a eu plus de synthèse d'amas d'or que tout autre élément, en raison de ses propriétés et de sa stabilité. Dans les sous-sections qui suivent, nous limitons notre discussion à des sujets spécifiques liés aux formules magiques et aux types de clusters.

Groupes FCC

Huit des métaux de transition cristallisent dans la structure fcc, voir le tableau 21 ci-dessous, y compris les métaux nobles plasmoniques et d'importants éléments catalytiquement actifs. La grande majorité de la synthèse des nanoclusters a été réalisée avec ces éléments. Les références de la synthèse des éléments fcc avec différentes formes et tailles sont données dans le tableau 21.

Les alliages de ces éléments sont également intéressants, mais les références de ceux-ci sont trop nombreuses pour être citées ici. Fréquemment, les formes communes synthétisées sont des cubes, des octaèdres, des cuboctaèdres et des icosaèdres. Typiquement, les clusters avec des facettes (111) sont plus faciles à synthétiser, car la surface (111) a généralement une énergie plus faible que la surface (100) [7]. On constate pour le dodécaèdre rhombique fcc qu'il existe des formules paires et impaires. Ceux-ci sont en accord avec ceux de [1], si l'on remplace le "n ” dans nos formules paires par 2(m -1). Les formules pour les fcc cuboctaèdres répertoriées dans [24] produisent les mêmes nombres magiques que les nôtres mais sont décalées de 1 car elles numérotent les coquilles comme n =1,2,… et on utilise la numérotation n =0,1,…. Nos formules magiques sont en accord avec celles de [2, 4], et par respect pour les travaux publiés précédemment, et pour maintenir la continuité des mathématiques, nous utilisons la notation [2, 4]. Les 5 formes de cluster fcc et leurs formules magiques associées apparaissent ci-dessous.

Clusters BCC

Sept des métaux de transition du tableau périodique ont la structure bcc, voir le tableau 21. Parmi les éléments magnétiques Fe, Co et Ni, seul le fer est bcc. Les nanocubes de fer semblent être la seule forme d'amas bcc synthétisée à ce jour [25]. Bien que la structure globale du fer soit bcc, des nanoclusters de fcc ont été synthétisés [26]. Cette référence analyse également la stabilité thermodynamique des amas. Nous présentons ici 5 formes de cluster bcc et leurs formules magiques associées.

Groupes HCP

Douze métaux de transition ont la structure hcp, voir le tableau 21. Cependant, nombre d'entre eux s'oxydent ou manquent d'intérêt scientifique pour être synthétisés. En ce qui concerne la forme d'amas bipyramidale hexagonale du tableau 11, des amas d'or ont été synthétisés [27]. La bipyramide hexagonale tronquée apparentée semble n'avoir été formée que par α −Fe₂ O₃ [28].

Amas platoniques

Les solides platoniciens sont connus depuis les anciens Grecs. Ils comprennent le cube, le tétraèdre, l'octaèdre, l'icosaèdre et le dodécaèdre. Dans les tableaux précédents, nous avons répertorié les formules magiques pour les cubes fcc et bcc et les octaèdres. Nous listons ici les formules de l'icosaèdre, du dodécaèdre, du tétraèdre et du tétraèdre centré sur le corps. Comme mentionné précédemment dans la section « Méthodes », le dodécaèdre est unique pour les clusters analysés ici, en ce que c n _s =7 se réfère à la fois aux atomes de surface et en vrac. Nous avons montré sur la figure 1b que l'enveloppe externe contient à la fois des atomes coordonnés cinq fois et six fois. Lorsqu'une coquille devient interne, ces atomes coordonnés cinq et six fois deviennent coordonnés sept et huit fois avec des liaisons à une coquille de chaque côté. De plus, les atomes de la coquille extérieure coordonnés par six sont coordonnés par sept en se liant à la coquille à l'intérieur. Ainsi, il y a sept fois des atomes coordonnés en surface et en masse pour le dodécaèdre. Chaque coquille dans la structure a 12 atomes de coquille quintuple, qui produisent 12n -12 atomes en vrac coordonnés sept fois. Le reste de la coordination septuple sont des atomes de surface.

Il a été démontré que les nanoclusters d'or prennent les formes platoniciennes [29]. Cette référence comprend le cube, le tétraèdre, l'octaèdre et l'icosaèdre. Plus tard, le nanocluster de dodécaèdre doré a également été synthétisé [30]. Ici, nous montrons à la fois le tétraèdre régulier, qui est « de type fcc » dans ce c _M =12 comme dans les structures fcc, et le tétraèdre centré sur le corps dans le tableau 16, où les atomes verts ont des liaisons simples. Les formules magiques platoniciennes sont présentées ci-dessous.

Amas de diamant cubique, simple cubique et décaèdre

Les éléments silicium et germanium ont le réseau cubique du diamant, ainsi que le diamant allotrope du carbone. En particulier, le silicium à terminaison hydrogène a suscité un intérêt récent. La surface à terminaison hydrogène (100), conduisant à des formes cubiques en grappes, a été déterminée comme ayant la plus faible énergie [31]. La synthèse de nanocubes Si-H de 8 à 15 nm a été réalisée [32]. Le tableau 17 montre un diagramme des clusters Si-H à terminaison hydrogène, avec des atomes d'hydrogène à simple liaison en vert. Si un nanocluster prend la forme cubique du diamant, il y aura des liaisons pendantes simples, qui doivent être passivées pour aider à maintenir la structure. En regardant les formules magiques, nous suggérons que la composition de tels amas Si-H est \(\phantom {\dot {i}\!}\text {Si}_{8n^{3}+6n^{2}-9n +5}\text {H}_{12n-8}\), où n est le nombre de coquilles dans le cluster. De tels points quantiques semi-conducteurs peuvent être intéressants pour les propriétés optiques, et la variation de la bande interdite avec la taille des amas à terminaison hydrogène a été déterminée comme étant inversement proportionnelle à la taille des amas [33].

La structure de réseau cubique simple a déjà été analysée par d'autres [4], bien que sans les détails que nous fournissons. Nous avons précédemment étudié le d formes hypercubes -dimensionnelles [14]. Le polonium est le seul élément qui reprend la structure cubique simple. Il est radioactif, ce qui peut conduire à des applications spécialisées. Nous présentons ici les formules magiques du diamant cubique, cubique simple et décaédrique.

Formules topologiques magiques

La complexité structurelle mesurée dans les cristaux peut nous donner une idée de la simplicité ou de la complexité de la structure et l'utilisation appropriée peut classer les structures pertinentes. Pour de tels classements, il est utile de considérer la description graphique du réseau cristallin, comme mentionné dans la section « Méthodes ». La complexité topologique des structures cristallines est mesurée par la distribution en degrés de sommet du graphe, I _vd [34], à l'aide du logiciel ToposPro, version 5.3.2.2 [35] :

où un _i est le degré (coordination) du i le sommet et la sommation s'effectuent le long de tout le v sommets, du graphe du quotient. Ce paramètre utilise un cristal infini par opposition aux clusters que nous avons considérés, mais est utile pour mesurer la complexité relative de différentes structures cristallines. Ainsi, plus le nombre est élevé, ou plus le contenu d'information du graphique est important, plus il est complexe. Dans le tableau 22, nous montrons les valeurs de I _vd obtenu de ToposPro dérivé des fichiers caf pour les structures cristallines dans la base de données ouverte cristallographique. Le polonium est le seul élément qui cristallise dans la structure cubique simple et la valeur est zéro, c'est-à-dire que le graphe du quotient a un sommet et zéro arêtes, en accord avec ce que nous attendons, que la structure cubique simple est bien la structure la moins complexe. Le sel, NaCl, est également représenté, avec deux éléments dans la structure cubique simple, ainsi que le silicium dans le cubique diamant, l'or dans le fcc, le fer dans le bcc et le cobalt dans les structures hcp. Nous mentionnons qu'une autre mesure de complexité liée à l'entropie de Shannon [34] n'est pas utile car cette mesure pour tous les éléments est identiquement nulle.

Une méthode similaire à celle décrite dans la section « Méthodes » pour déterminer les formules magiques peut être appliquée pour les formules magiques décrivant les indices topologiques. Seulement ici, les degrés des polynômes sont 7, 8 ou 9, donc leurs valeurs pour au moins 10 n consécutifs - les valeurs doivent être calculées. Ensuite, un problème d'interpolation d'un degré supérieur donne le résultat. Étant donné que la résolution d'un système linéaire de taille 10×10 avec la boîte à outils symbolique nécessite un certain temps, tous les coefficients des indices topologiques peuvent être calculés simultanément en utilisant plusieurs membres de droite pour obtenir les coefficients de tous les polynômes.

Les formules magiques pour les indices topologiques sont détaillées dans les tableaux 23, 24 et 25. Les quatre indices que nous analysons ne dépendent que de n , le nombre de coques dans le cluster. En regardant les résultats, le réseau cubique simple, en tant que structure la moins complexe, a également les formules « les plus simples ». Malgré nos efforts, nous ne parvenons pas à résoudre l'indice de Szeged des cubes bcc. Aucune solution stable n'a été trouvée. En général, les structures fcc sont plus faciles à résoudre pour les formules topologiques. Nous n'avons pu résoudre aucune structure hcp et seulement quelques structures bcc. Cela peut être lié à la complexité topologique car le réseau fcc est plus simple que le bcc ou le hcp, voir le tableau 22. Dans les tableaux, nous fournissons des formules pour le cuboctaèdre, l'icosaèdre et le décaèdre. Nous avons précédemment [12] fourni des tableaux de données numériques pour ces indices, avec la mise en garde que le cuboctaèdre dans [12] avait des nombres magiques différents. Ici, nous voyons que les données tabulées peuvent être résumées succinctement sous forme de formules magiques. Aussi le degré du polynôme de l'indice suit les règles de l'espace 3D [14]. Certains indices topologiques pour les solides platoniciens ont déjà été publiés [36]. À partir de cette référence, nous vérifions l'indice de Wiener pour les cinq solides pour n =1. L'indice de Wiener pour les rangées de mailles unitaires du réseau fcc a été étudié [37], mais nos résultats ne peuvent être comparés puisque nous étudions les clusters.

Dispersion

Le pourcentage d'atomes de surface (dispersion, FE) des différents clusters est présenté sur la Fig. 2. Les nanoclusters de platine sont connus pour avoir une activité catalytique vis-à-vis de la réaction de réduction de l'oxygène (ORR) qui dépend de la taille et de la forme [38]. Cette référence a déterminé que les amas cuboctaédriques de platine d'une taille de 2,2 nm avaient une activité ORR maximale. Il est également connu que pour les alliages PtNi, la surface (111) est préférée pour l'ORR [39]. Nous comparons les amas icosaédriques, octaédriques, décaédriques et cuboctaédriques pour FE à un d _rel =7,5 pour le platine à 2,2 nm. Les amas icosaédriques, octaédriques et décaédriques ont des surfaces avec des faces (111). En utilisant les lois de puissance de la Fig. 2, nous trouvons pour le d donné _rel que le FE pour les amas icosaédriques est de 47,9%, pour le cuboctaèdre de 52,8% et pour le décaèdre de 57,5% et que les amas octaédriques ont FE=58,9% . Ainsi, en fonction de la forme, les amas octaédriques ont à la fois la surface (111) et la valeur la plus élevée de FE pour une taille similaire. Le coefficient et l'exposant de la loi de puissance sont tous deux pertinents pour la détermination de FE pour un petit d _rel . L'interprétation mathématique de l'exposant de la loi de puissance donne la signification physique comme la relation de l'ordonnée, FE, aux abscisses, d _rel , ou la variation relative en pourcentage de FE par rapport à la variation relative en pourcentage de d _rel . Le coefficient de loi de puissance est simplement la valeur de FE lorsque d _rel =1.

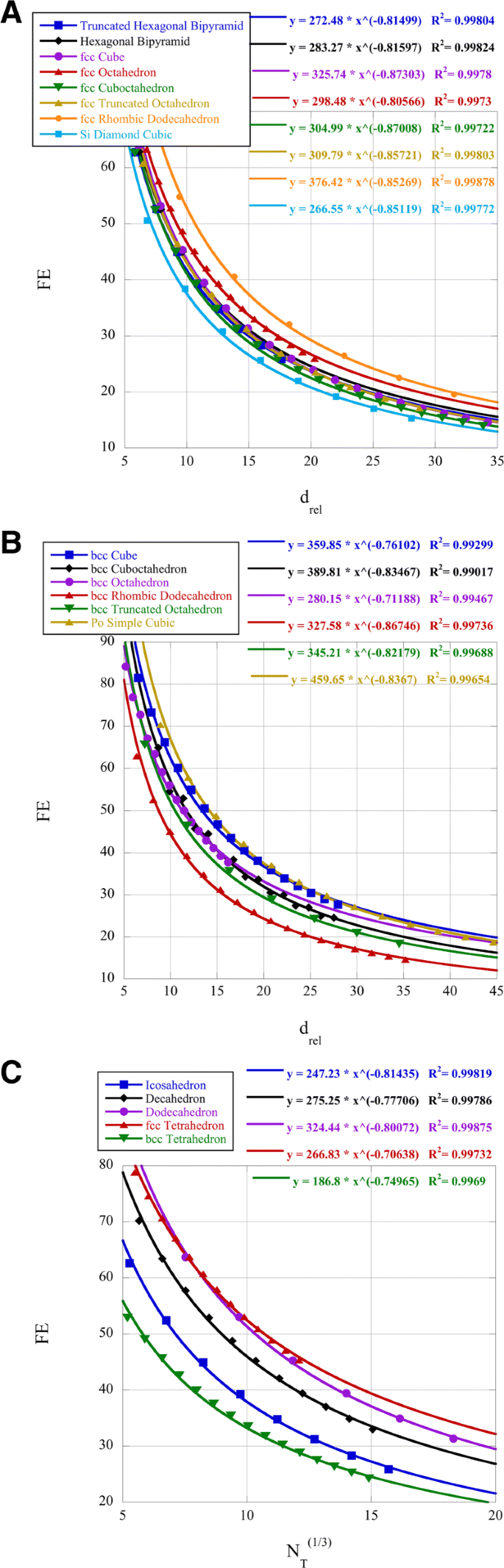
Dispersion FE pour les nanoclusters

Un autre groupe de recherche a synthétisé des amas icosaédriques en alliage de platine et comparé l'activité avec des amas octaédriques [40]. Ces nanoclusters avaient une taille d'environ 13 nm ou N =20 000 pour les amas octaédriques et N =15,000 pour les amas icosaédriques. Cela produit un d _rel =30 pour les amas octaédriques et 25 pour les icosaédriques. En utilisant les lois de puissance pertinentes, cela donne FE=18.0% pour les amas octaédriques et 19,8 % pour les amas icosaédriques. Il y a très peu de différence de FE pour cette taille d'amas, mais l'amas icosaédrique a une contrainte importante due au jumelage, ce qui peut déplacer le centre de la bande d, affectant ainsi les résultats ORR [40]. Cependant, étant donné les données dépendantes de la taille de [38], il peut être suggéré que des grappes plus petites produiraient des données ORR encore plus élevées. En effet, 4 nm Pt₃ Les octaèdres de Ni, lorsqu'ils sont dopés au Mo, ont produit des résultats ORR records [41].

Conclusions

Nous avons étudié 19 types de nanoclusters et quelques formules magiques pertinentes pour le nombre d'atomes, de liaisons, de nombres de coordination et d'indices topologiques. Ceux-ci incluent le fcc, le bcc, le hcp, les solides platoniciens, le diamant cubique, le cubique simple et les amas décaédriques. La majorité de ces résultats sont plus détaillés que ce qui avait été déterminé précédemment, et un grand nombre sont dénombrés pour la première fois. L'un des grands objectifs de la recherche sur les matériaux est la corrélation de la structure avec les propriétés. Cette étude détaillée des relations magiques pour les nanoclusters est un pas dans cette direction. Un exemple est la discussion de la dispersion des atomes de surface et de sa relation avec l'activité catalytique. Notre intention est que ces résultats aident les scientifiques dans leurs études sur la structure des nanoclusters et les propriétés associées.

Abréviations

cci :

cubique centré

cif :

fichier d'informations cristallographiques

fcc :

cubique à faces centrées

FE :

Fraction exposée, dispersion

hcp :

hexagonal fermé emballé

ORR :

Réaction d'oxydo-réduction

rW(G) :

Indice de Wiener inversé

Sz(G) :

Index Szeged

W(G) :

Indice de Vienne

WW(G) :

Indice Hyper-Wiener