Comprendre les formules d'entraînement et la rétropropagation pour les perceptrons multicouches

Cet article présente les équations que nous utilisons lors des calculs de mise à jour du poids, et nous discuterons également du concept de rétropropagation.

Bienvenue dans la série d'AAC sur l'apprentissage automatique.

Retrouvez la série jusqu'à présent ici :

1. Comment effectuer une classification à l'aide d'un réseau de neurones :qu'est-ce que le perceptron ?
2. Comment utiliser un exemple simple de réseau neuronal Perceptron pour classer des données
3. Comment former un réseau de neurones Perceptron de base
4. Comprendre la formation simple sur les réseaux neuronaux
5. Une introduction à la théorie de la formation pour les réseaux de neurones
6. Comprendre le taux d'apprentissage dans les réseaux de neurones
7. Apprentissage automatique avancé avec le Perceptron multicouche
8. La fonction d'activation sigmoïde :activation dans les réseaux de neurones Perceptron multicouches
9. Comment former un réseau de neurones Perceptron multicouches
10. Comprendre les formules d'entraînement et la rétropropagation pour les perceptrons multicouches
11. Architecture de réseau neuronal pour une implémentation Python
12. Comment créer un réseau de neurones Perceptron multicouche en Python
13. Traitement du signal à l'aide de réseaux de neurones :validation dans la conception de réseaux de neurones
14. Entraînement d'ensembles de données pour les réseaux de neurones :comment entraîner et valider un réseau de neurones Python

Nous avons atteint le point où nous devons examiner attentivement un sujet fondamental au sein de la théorie des réseaux de neurones :la procédure de calcul qui nous permet d'affiner les poids d'un Perceptron multicouche (MLP) afin qu'il puisse classer avec précision les échantillons d'entrée. Cela nous mènera au concept de « rétropropagation », qui est un aspect essentiel de la conception de réseaux de neurones.

Mise à jour des poids

L'information entourant la formation des MLP est compliquée. Pour aggraver les choses, les ressources en ligne utilisent une terminologie et des symboles différents, et elles semblent même donner des résultats différents. Cependant, je ne sais pas si les résultats sont vraiment différents ou présentent simplement les mêmes informations de différentes manières.

Les équations contenues dans cet article sont basées sur les dérivations et les explications fournies par le Dr Dustin Stansbury dans cet article de blog. Son traitement est le meilleur que j'ai trouvé, et c'est un excellent point de départ si vous souhaitez approfondir les détails mathématiques et conceptuels de la descente de gradient et de la rétropropagation.

Le schéma suivant représente l'architecture que nous allons implémenter dans le logiciel, et les équations ci-dessous correspondent à cette architecture, qui est discutée plus en détail dans le prochain article.

Terminologie

Ce sujet devient rapidement ingérable si nous ne maintenons pas une terminologie claire. J'utiliserai les termes suivants :

• Préactivation (abrégé \(S_{preA}\) ) :Cela fait référence au signal (en fait juste un nombre dans le contexte d'une itération d'apprentissage) qui sert d'entrée à la fonction d'activation d'un nœud. Il est calculé en effectuant un produit scalaire d'un tableau contenant des poids et d'un tableau contenant les valeurs provenant des nœuds de la couche précédente. Le produit scalaire équivaut à effectuer une multiplication élément par élément des deux tableaux, puis à additionner les éléments du tableau résultant de cette multiplication.
• Postactivation (abrégé \(S_{postA}\) ):Cela fait référence au signal (encore une fois, juste un nombre dans le contexte d'une itération individuelle) qui sort d'un nœud. Il est produit en appliquant la fonction d'activation au signal de préactivation. Mon terme préféré pour la fonction d'activation, noté \(f_{A}()\) , est logistique plutôt que sigmoïde.
• Dans le code Python, vous verrez des matrices de poids étiquetées ItoH et HtoO . J'utilise ces identifiants parce qu'il est ambigu de dire quelque chose comme « poids de la couche cachée » :s'agirait-il des poids qui sont appliqués avant le calque caché ou après la couche cachée ? Dans mon schéma, ItoH spécifie les poids qui sont appliqués aux valeurs transférées des nœuds d'entrée aux nœuds cachés, et HtoO spécifie les poids qui sont appliqués aux valeurs transférées des nœuds cachés au nœud de sortie.
• La valeur de sortie correcte pour un échantillon d'apprentissage est appelée cible et est noté T .
• Taux d'apprentissage est abrégé en LR .
• Erreur finale est la différence entre le signal de postactivation du nœud de sortie (\(S_{postA,O}\) ) et la cible, calculée comme \(FE =S_{postA,O} - T\) .
• Signal d'erreur (\(S_{ERREUR}\) ) est l'erreur finale propagée vers la couche cachée via la fonction d'activation du nœud de sortie.
• Dégradé représente la contribution d'un poids donné au signal d'erreur. On modifie les poids en soustrayant cette contribution (multipliée par le taux d'apprentissage si besoin).

Le schéma suivant situe certains de ces termes dans la configuration visualisée du réseau. Je sais, ça ressemble à un gâchis multicolore. Je m'excuse. C'est un diagramme riche en informations, et bien qu'il puisse être un peu offensant à première vue, si vous l'étudiez attentivement, je pense que vous le trouverez très utile.

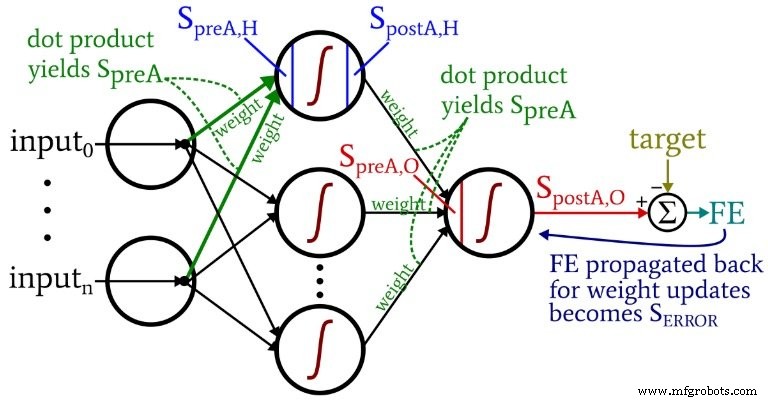
Les équations de mise à jour du poids sont dérivées en prenant la dérivée partielle de la fonction d'erreur (nous utilisons l'erreur quadratique sommée, voir la partie 8 de la série, qui traite des fonctions d'activation) par rapport au poids à modifier. Veuillez vous référer au message du Dr Stansbury si vous voulez voir les mathématiques; dans cet article, nous passerons directement aux résultats. Pour les poids masqués en sortie, nous avons les éléments suivants :

\[S_{ERROR} =FE \times {f_A}'(S_{preA,O})\]

\[gradient_{HtoO}=S_{ERROR}\times S_{postA,H}\]

\[poids_{HtoO} =poids_{HtoO}- (LR \times gradient_{HtoO})\]

Nous calculons le signa d'erreur l en multipliant l'erreur finale par la valeur qui est produite lorsque nous appliquons la dérivé de la fonction d'activation au signal de préactivation délivré au nœud de sortie (notez le symbole premier, qui indique la dérivée première, dans \({f_A}'(S_{preA,O})\)). Le gradient est ensuite calculé en multipliant le signal d'erreur par le signal de postactivation de la couche cachée. Enfin, nous mettons à jour le poids en soustrayant ce gradient à partir de la valeur de poids actuelle, et nous pouvons multiplier le gradient par le taux d'apprentissage si nous voulons changer la taille du pas.

Pour les poids d'entrée à caché, nous avons ceci :

\[gradient_{ItoH} =FE \times {f_A}'(S_{preA,O})\times weight_{HtoO} \times {f_A}'(S_{preA ,H}) \fois saisie\]

\[\Rightarrow gradient_{ItoH} =S_{ERROR} \times weight_{HtoO} \times {f_A}'(S_{preA,H})\times input\]

\[poids_{ItoH} =poids_{ItoH} - (LR \times gradient_{ItoH})\]

Avec les poids d'entrée à masqués, l'erreur doit être propagée à travers une couche supplémentaire, et nous le faisons en multipliant le signal d'erreur par le poids caché à la sortie connecté au nœud caché d'intérêt. Ainsi, si nous mettons à jour un poids d'entrée à caché qui mène au premier nœud caché, on multiplie le signal d'erreur par le poids qui relie le premier nœud caché au nœud de sortie. Nous terminons ensuite le calcul en effectuant des multiplications analogues à celles des mises à jour des poids masqués en sortie :nous appliquons la dérivée de la fonction d'activation au signal de préactivation du nœud caché , et la valeur « d'entrée » peut être considérée comme le signal de postactivation du nœud d'entrée.

Rétropropagation

L'explication ci-dessus a déjà abordé le concept de rétropropagation. Je veux juste renforcer brièvement ce concept et également m'assurer que vous avez une connaissance explicite de ce terme, qui apparaît fréquemment dans les discussions sur les réseaux de neurones.

La rétropropagation nous permet de surmonter le dilemme du nœud caché discuté dans la partie 8. Nous devons mettre à jour les poids d'entrée à caché en fonction de la différence entre la sortie générée par le réseau et les valeurs de sortie cibles fournies par les données d'apprentissage, mais ces poids influencent la sortie générée indirectement.

La rétropropagation fait référence à la technique par laquelle nous renvoyons un signal d'erreur vers une ou plusieurs couches cachées et mettons à l'échelle ce signal d'erreur en utilisant à la fois les poids émergeant d'un nœud caché et la dérivée de la fonction d'activation du nœud caché. La procédure globale sert à mettre à jour un poids en fonction de la contribution du poids à l'erreur de sortie, même si cette contribution est masquée par la relation indirecte entre un poids d'entrée à masqué et la valeur de sortie générée.

Conclusion

Nous avons couvert beaucoup de sujets importants. Je pense que nous avons des informations très précieuses sur la formation des réseaux de neurones dans cet article, et j'espère que vous êtes d'accord. La série va commencer à devenir encore plus excitante, alors revenez pour de nouveaux épisodes.