Comment former un réseau de neurones Perceptron multicouche

Nous pouvons grandement améliorer les performances d'un Perceptron en ajoutant une couche de nœuds cachés, mais ces nœuds cachés rendent également l'entraînement un peu plus compliqué.

Jusqu'à présent, dans la série AAC sur les réseaux de neurones, vous avez appris la classification des données à l'aide de réseaux de neurones, en particulier de la variété Perceptron.

Rattrapez-vous sur la série ci-dessous ou plongez dans cette nouvelle entrée qui expliquera les bases du réseau de neurones multicouches Perceptron (MLP).

1. Comment effectuer une classification à l'aide d'un réseau de neurones :qu'est-ce que le perceptron ?
2. Comment utiliser un exemple simple de réseau neuronal Perceptron pour classer des données
3. Comment former un réseau de neurones Perceptron de base
4. Comprendre la formation simple sur les réseaux neuronaux
5. Une introduction à la théorie de la formation pour les réseaux de neurones
6. Comprendre le taux d'apprentissage dans les réseaux de neurones
7. Apprentissage automatique avancé avec le Perceptron multicouche
8. La fonction d'activation sigmoïde :activation dans les réseaux de neurones Perceptron multicouches
9. Comment former un réseau de neurones Perceptron multicouches
10. Comprendre les formules d'entraînement et la rétropropagation pour les perceptrons multicouches
11. Architecture de réseau neuronal pour une implémentation Python
12. Comment créer un réseau de neurones Perceptron multicouche en Python
13. Traitement du signal à l'aide de réseaux de neurones :validation dans la conception de réseaux de neurones
14. Entraînement d'ensembles de données pour les réseaux de neurones :comment entraîner et valider un réseau de neurones Python

Qu'est-ce qu'un réseau de neurones Perceptron multicouche ?

L'article précédent a démontré qu'un Perceptron monocouche ne peut tout simplement pas produire le type de performances que nous attendons d'une architecture de réseau de neurones moderne. Un système limité à des fonctions linéairement séparables ne sera pas en mesure d'approcher les relations entrées-sorties complexes qui se produisent dans les scénarios de traitement du signal de la vie réelle. La solution est un Perceptron multicouche (MLP), comme celui-ci :

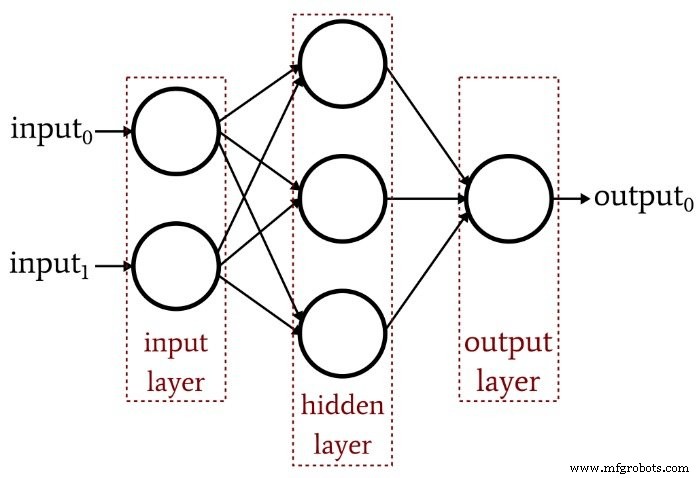
En ajoutant cette couche cachée, nous transformons le réseau en un « approximateur universel » qui peut réaliser une classification extrêmement sophistiquée. Mais nous devons toujours nous rappeler que la valeur d'un réseau de neurones dépend entièrement de la qualité de sa formation. Sans données de formation abondantes et diversifiées et une procédure de formation efficace, le réseau n'apprendra jamais à classer les échantillons d'entrée.

Pourquoi la couche cachée complique-t-elle l'entraînement ?

Regardons la règle d'apprentissage que nous avons utilisée pour entraîner un Perceptron monocouche dans un article précédent :

\[w_{new} =w+(\alpha\times(output_{expected}-output_{calculated})\times input)\]

Notez l'hypothèse implicite dans cette équation :nous mettons à jour les poids en fonction de la sortie observée, donc pour que cela fonctionne, les poids dans le Perceptron monocouche doivent influencer directement la valeur de sortie. C'est comme choisir la température de l'eau du robinet en tournant les deux boutons pour le chaud et le froid. La relation entre la température globale et l'action des boutons est assez simple, et même les personnes qui n'aiment pas les mathématiques peuvent trouver la température de l'eau souhaitée en jouant un peu avec les boutons.

Mais imaginez maintenant que le débit d'eau à travers les tuyaux chauds et froids est lié à la position du bouton d'une manière complexe et hautement non linéaire. Vous tournez régulièrement et lentement le bouton pour l'eau chaude, mais le débit résultant varie de manière erratique. Vous essayez le bouton pour l'eau froide et cela fait la même chose. Fixer la température idéale de l'eau dans ces conditions, d'autant plus que la « sortie » doit être obtenue grâce à une combinaison de deux relations de contrôle déroutantes, serait beaucoup plus difficile.

C'est ainsi que je comprends le dilemme de la couche cachée. Les poids qui connectent les nœuds d'entrée aux nœuds cachés sont conceptuellement analogues à ces boutons mécaniquement erratiques - parce que les poids d'entrée à caché n'ont pas de chemin direct vers la couche de sortie, la relation entre ces poids et la sortie du réseau est si complexe que la règle d'apprentissage simple indiquée ci-dessus ne sera pas efficace.

Un nouveau paradigme de formation

Étant donné que la règle d'apprentissage originale de Perceptron ne peut pas être appliquée aux réseaux multicouches, nous devons repenser notre stratégie de formation. Ce que nous allons faire, c'est incorporer la descente de gradient et la minimisation d'une fonction d'erreur.

Une chose à garder à l'esprit est que cette procédure de formation n'est pas spécifique aux réseaux de neurones multicouches. La descente de gradient provient de la théorie générale de l'optimisation, et la procédure de formation que nous employons pour les MLP est également applicable aux réseaux monocouche. Cependant, si je comprends bien, la descente de gradient de style MLP est (au moins théoriquement) inutile pour un Perceptron monocouche, car la règle la plus simple illustrée ci-dessus finira par faire le travail.

Déduire les équations de mise à jour du poids réelles pour un MLP implique des calculs intimidants que je n'essaierai pas d'expliquer intelligemment à ce stade. Mon objectif pour le reste de cet article est de fournir une introduction conceptuelle à deux aspects clés de la formation MLP - la descente de gradient et la fonction d'erreur - puis nous continuerons cette discussion dans le prochain article en incorporant une nouvelle fonction d'activation.

Descente de dégradé

Comme son nom l'indique, la descente de gradient est un moyen de descendre vers le minimum d'une fonction d'erreur basée sur la pente. Le diagramme ci-dessous montre la manière dont un gradient nous donne des informations sur la façon de modifier les poids - la pente d'un point sur la fonction d'erreur nous indique dans quelle direction nous devons aller et à quelle distance nous sommes du minimum.

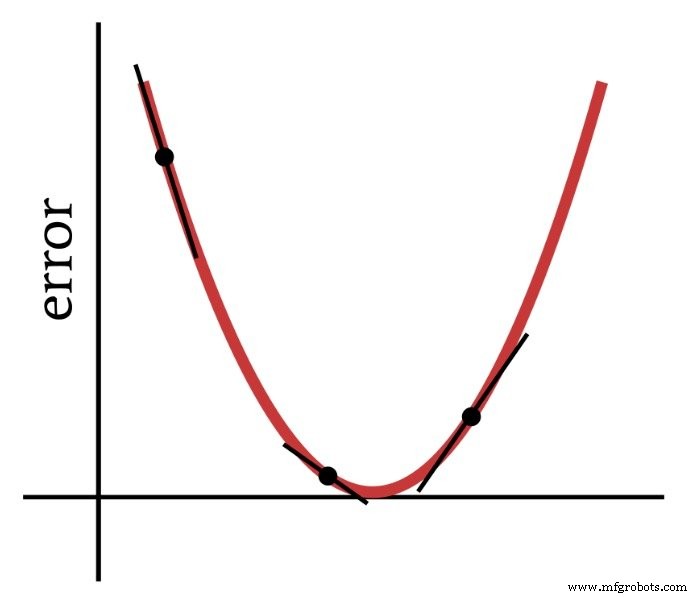
Ainsi, la dérivée de la fonction d'erreur est un élément important des calculs que nous utilisons pour entraîner un Perceptron multicouche. En fait, nous aurons besoin de partiel dérivés ici. Lorsque nous implémentons la descente de gradient, nous rendons chaque modification de poids proportionnelle à la pente de la fonction d'erreur par rapport au poids en cours de modification.

La fonction d'erreur (fonction de perte AKA)

Une méthode courante de quantification de l'erreur d'un réseau de neurones consiste à mettre au carré la différence entre la valeur attendue (ou "cible") et la valeur calculée pour chaque nœud de sortie, puis à additionner toutes ces différences au carré. Vous pouvez appeler cela « somme de la différence au carré » ou « erreur quadratique sommée » ou peut-être diverses autres choses, et vous verrez également l'abréviation LMS, qui signifie la moindre moyenne, car le but de la formation est de minimiser la moyenne erreur au carré. Cette fonction d'erreur (notée E) peut être exprimée mathématiquement comme suit :

\[E=\frac{1}{2}\sum_k(t_k-o_k)^2\]

où k indique la plage de nœuds de sortie, t est la valeur de sortie cible et o est la valeur de sortie calculée.

Conclusion

Nous avons jeté les bases d'un entraînement réussi d'un Perceptron multicouche, et nous continuerons à explorer ce sujet intéressant dans le prochain article.