Fonctionnement monomode stable du laser à cascade quantique à rétroaction distribuée grâce à des revêtements à facettes à réflectivité optimisée

Contexte

Les lasers à cascade quantique dans l'infrarouge moyen (QCL) [1] sont l'une des sources lumineuses les plus prometteuses pour de nombreuses applications commerciales. Ces applications pratiques telles que la détection de gaz, la communication en espace libre et la spectroscopie haute résolution [2,3,4,5] nécessiteraient une QCL avec une puissance élevée, une fiabilité monomode améliorée et un faible coût. En conséquence, depuis que la première rétroaction distribuée (DFB)-QCL a été démontrée en 1997 [6], les performances de ces dispositifs ont été fortement améliorées avec la démonstration du fonctionnement en onde continue (CW) à température ambiante avec une puissance élevée à travers le région de l'infrarouge moyen [7,8,9,10]. Cependant, la plupart des DFB-QCL basés sur une structure de réseau enterrée auraient le problème de facettes clivées aléatoires qui déterminent le mode de fréquence laser. En raison de la même quantité de perte dans deux modes de bord de bande, un fonctionnement monomode stable ne peut pas être garanti [11]. Surtout dans des conditions de température élevée ou de courant d'injection important, des sauts de mode se produisent toujours, ce qui est préjudiciable aux applications dans ces dispositifs monomodes.

Pour obtenir un fonctionnement monomode stable, un déphasage quart d'onde (λ/4 PS) a été introduit en période de réseau afin que le laser puisse fonctionner en mode défaut; ainsi, la concurrence entre les deux modes de limite de bande peut être évitée. Mais la lithographie par faisceau d'électrons doit être utilisée pour la fabrication du réseau λ/4 PS, ce qui est long et coûteux [12]. Le laser DFB à couplage de gain est un bon choix pour obtenir un fonctionnement monomode stable pour le laser à semi-conducteur conventionnel [13]. Cependant, il n'est pas réaliste pour QCL de fabriquer les lasers DFB à couplage de gain en raison de la grande perte causée par la région active gravée. Une autre méthode astucieuse consiste à utiliser le mécanisme de couplage de perte de cavité pour augmenter la perte de différence entre deux modes DFB. On pense qu'un revêtement à facettes à réflectivité approprié peut obtenir un fonctionnement monomode stable même à des températures élevées et à des courants importants. Bien que certaines recherches soient consacrées au revêtement de facettes, elles se concentrent toujours sur la formation d'une longueur de cavité équivalente optimale L _option pour préserver l'efficacité des prises murales (WPE) pour les lasers plutôt que la fiabilité monomode [14, 15]. De plus, le revêtement de réflectivité optimisé devrait être un moyen prometteur pour résoudre la compétitivité entre deux modes DFB et intéressant à étudier systématiquement.

Dans cet article, fonctionnement monomode stable des DFB-QCL à λ ~ 4,76 m est présenté après revêtement antireflet (AR)/haute réflexion (HR). Le revêtement AR est constitué d'un diélectrique à double couche d'Al₂ O₃ (380 nm) et Ge (33 nm). Ces appareils affichent une densité de courant de seuil très faible de 0,65 kA/cm ² à 20 °C. L'émission monomode avec un taux de suppression de mode latéral (SMSR) supérieur à 26 dB est obtenue jusqu'à une température de 90 °C en fonctionnement CW sans aucun saut de mode. On pense que le revêtement antireflet sur la face avant est très utile pour supprimer la phase aléatoire de la facette de la cavité.

Méthodes

Théorie et simulation

Le cœur de la simulation sur l'effet de revêtement antireflet dans une cavité DFB finie est le calcul de la perte de mode pour deux modes de bord de bande. La méthode de la matrice de transfert serait un moyen approprié pour analyser l'ensemble de la structure laser [16, 17]. Nous considérons l'application de cette méthode à des dispositifs qui ont un profil d'indice de réfraction longitudinal similaire à celui montré sur la figure 1. Ce dessin schématique illustre l'effet du réseau avec une petite perturbation de l'indice effectif différent (n _eff,1 , n _eff,2 ) et films couchés (n ₃ , n ₄ ) sur le mode guidé. Les indices de réfraction complexes des principaux matériaux utilisés dans le calcul sont répertoriés comme suit :InP (3.088 + i*2e−4), InGaAs (3.4 + i*2.9e−5), région active (3.298 + i*4e−5), InP fortement dopé (2.81 + i*1.4e−2), SiO₂ (1.3603 + i*6.3e−4), Au (1.341 + i*32.582), Al₂ O₃ (1.5348 + i*3.2967e−3), et Ge (4.0165 + i*4e−2). Ensuite, les différents indices effectifs n _eff,1 = 3.1599 + i*5.17e−5 et n _eff,2 = 3.1662 + i*5.6756e−5 ont été calculés avec COMSOL par la fonction d'équation aux dérivées partielles (PDE). Le laser est supposé fonctionner dans un seul mode transverse de sorte que les caractéristiques de propagation de la lumière en chaque point le long de la cavité laser soient décrites par une seule quantité complexe scalaire, k , qui est le vecteur d'onde du milieu. On considère en outre que le laser est polarisé linéairement et que son champ électrique associé a une dépendance temporelle sinusoïdale e ^{i t} . Suivant ces hypothèses données ci-dessus, un facteur d'onde électromagnétique plan unidimensionnel E _z , qui décrit la partie de variation spéciale de la fonction d'onde, satisfait l'équation de Helmholtz

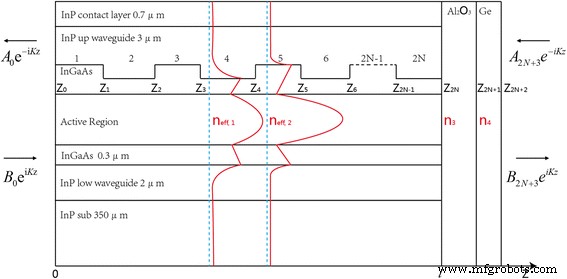
Schéma illustrant le modèle de cavité DFB finie avec revêtement antireflet sur le profil de mode optique longitudinal

K (z) est donné par

où ω et c sont respectivement la fréquence angulaire et la vitesse de la lumière et n (z) est l'indice de réfraction complexe en chaque point le long de la cavité laser. Le vecteur d'onde k qui doit être résolu peut être divisé en deux parties :k _r et k _je . La vraie partie k _r détermine la longueur d'onde de la lumière dans la cavité laser, tandis que la partie imaginaire k _je provient de la perte de mode de la cavité finie qui explique l'atténuation. A partir de la Fig. 1, on peut voir que le laser peut être considéré comme un dispositif multi-sections avec 2N + 2 sections où N est la période de râpage. Dans chacune de ces sections, le champ électrique E _n (z) est une combinaison linéaire de deux ondes planes exponentiellement contra-propagatives où l'une est décroissante avec une amplitude complexe A _n et l'autre augmente avec B _n . L'équation est décrite comme suit :

Au total, il y a 2N + 3 interfaces. A chacune de ces interfaces, le champ électrique et sa dérivée par rapport à la direction de propagation doivent être égaux des deux côtés de l'interface. L'équation est obtenue comme suit :

La matrice de transfert M (d _n ) est donné par

Étant donné que le laser à pompage électrique est un dispositif auto-oscillant, il n'y a pas d'ondes entrantes provenant de l'extérieur de l'appareil. Il en résulte la condition aux limites B ₀ = A _{2N + 3} = 0, et l'équation devient

Chaque valeur du vecteur d'onde k peut être obtenu à l'aide de Matlab via Eq. (6). Les parties imaginaires k _je correspondant aux pertes des modes de cavité aiderait à analyser les effets de revêtement AR.

La figure 2a montre les résultats calculés sur la base d'une simulation de matrice de transfert. Comme l'ont montré les deux courbes rouges, la perte du mode haute fréquence change très lentement avec la diminution de la réflectivité alors que le mode basse fréquence augmente fortement. L'encart montre le profil de mode calculé pour les modes basse et haute fréquence, pour une seule période du réseau. Comme tracé, le mode basse fréquence a une amplitude de champ électrique plus élevée dans les pics de réseau qui est la partie d'indice le plus élevé du réseau, et également, le mode haute fréquence est plus concentré dans la partie d'indice inférieur du réseau. Pour un modèle à cavité infinie sans réflectivité de facette, le mode haute fréquence a toujours une perte de mode plus faible que le mode basse fréquence. Si l'effet des miroirs à facettes d'extrémité peut être ignoré, alors le mode haute fréquence avec les pertes de guide d'ondes les plus faibles sera toujours laser. Cependant, la présence de miroirs à facettes d'extrémité donne des réflexions qui interfèrent de manière constructive ou destructive avec les modes DFB dans la cavité laser. Cette interférence affecte la perte finie de la cavité réseau de chaque mode et peut déterminer quel mode est laser. Nous notons que l'effet des miroirs est le plus important lorsque la position des deux miroirs coïncide avec un pic d'amplitude de champ électrique d'un mode DFB, ce qui est également lorsque les miroirs sont à un nœud pour l'autre mode DFB. Ici, les miroirs de la facette non revêtue coïncident avec le pic du mode basse fréquence, puis les réflexions des miroirs d'extrémité interfèrent de manière constructive au maximum avec le mode présent dans la cavité laser. Il en résulte une diminution de la perte de mode totale, en raison de la contribution constructive du miroir. Au fur et à mesure que la réflectivité diminue et que le déphasage supplémentaire influence l'utilisation du revêtement AR à double couche, la perte du mode basse fréquence augmente progressivement avec la diminution de la réflectivité en raison de l'affaiblissement de l'effet d'interférence et de l'augmentation de la perte de miroir. Pendant ce temps, la perte du mode haute fréquence a légèrement changé en raison de l'effet d'interférence amélioré. Il en résulte que la perte de mode est aussi similaire qu'une fonction exponentielle, en particulier lorsque la réflectivité de la facette avant est <0,15. Selon la simulation, il n'existe qu'un seul point minimum dans tout le spectre lorsque la réflectivité de la facette avant est < 0.11, ce qui signifie qu'un saut de mode ne peut pas se produire en théorie car une autre perte de mode de bord de bande est trop élevée pour être laser.

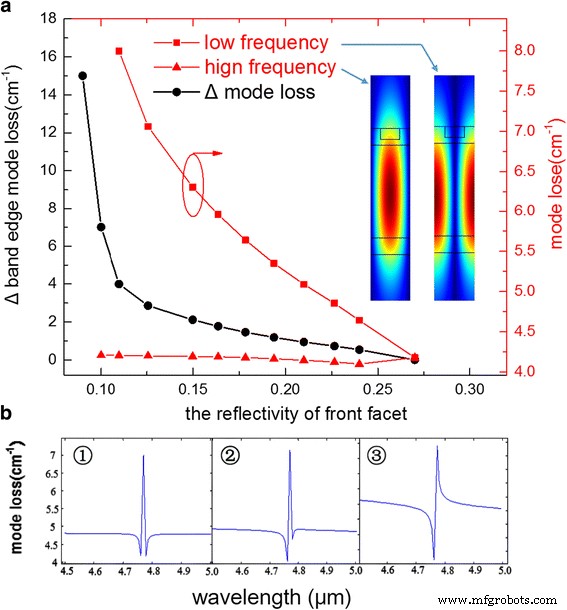
un Les deux courbes rouges sont respectivement la perte de mode du mode haute et basse fréquence. La courbe noire est la perte de mode différentielle entre les deux modes de bord de bande étiquetés . L'encart montre le profil de mode calculé pour les modes basse et haute fréquence, pour une seule période du réseau. b Le spectre de perte de mode calculé sur la base d'une simulation de matrice de transfert avec différents revêtements AR

La figure 2b montre les trois spectres de perte de mode typiques pendant la simulation où les modes haute et basse fréquence sont respectivement de 4,762 et 4,779 m. Le premier est le DFB-QCL sans revêtement AR. Nous pouvons voir clairement la bande d'arrêt provenant de la rétroaction du réseau et les deux modes de bord de bande sont presque les mêmes. Le second est un revêtement AR spécifique avec 200 nm d'Al₂ O₃ et 5 nm Ge avec une réflectivité de 0,22. Le différentiel entre les deux modes de bord de bande commence à être évident. Le dernier montre qu'avec un revêtement à faible réflectivité, la perte de mode est si importante que le mode basse fréquence est submergé par la perte de bande d'arrêt. Bien que la réflectivité plus faible, la plus grande perte de mode Δ en théorie, nous devrions également considérer que la réflectivité extrêmement faible provoque une perte de miroir énorme dans les dispositifs qui ferait chuter brusquement le WPE. C'est un compromis pour choisir l'épaisseur du film en fonction de l'expérience.

Fabrication d'appareils

La plaquette QCL a été cultivée sur une plaque dopée n (Si, 3 × 10 ¹⁷ cm ⁻³ ) Substrat InP par épitaxie par faisceau moléculaire (MBE) à source solide basée sur une conception de résonance à deux phonons. Le noyau actif comprend 40 étages de compensation de contrainte In_0.669 Ga_0.331 As/In_0.362 Al_0.638 En tant que puits et barrières quantiques, similaires à la Réf. [18]. L'ordre des couches était le suivant :couche de gaine InP inférieure de 2 μm (Si, 2,5 × 10 ¹⁶ cm ⁻³ ), 0,3 μm d'épaisseur apparié en _0,47 Ga_0,53 Comme couche (Si, 4 × 10 ¹⁶ cm ⁻³ ), 40 étages actifs/injecteurs, 0,3 μm d'épaisseur In_0,47 Ga_0,53 Comme couche (Si, 4 × 10 ¹⁶ cm ⁻³ ), couche supérieure de gaine InP 3μm (Si, 2,5 × 10 ¹⁶ cm ⁻³ ), et une couche de gaine InP fortement dopée de 0,7 µm (Si, 5 × 10 ¹⁸ cm ⁻³ ). Le niveau de dopage moyen de la région active a été ajusté empiriquement à 2,4 × 10 ¹⁶ cm ⁻³ . Pour fabriquer le réseau enterré, le revêtement supérieur a été retiré jusqu'à la couche supérieure d'InGaAs. Le réseau DFB du premier ordre de période Λ = 0,755 m (cycle d'utilisation σ =20%) a été définie sur la couche supérieure d'InGaAs de 300 nm d'épaisseur en utilisant la technique de lithographie holographique et ensuite gravée à une profondeur d'environ 90 nm par gravure chimique humide. Ensuite, un faible dopé de 3μm d'épaisseur (Si, 2,5 × 10 ¹⁶ cm ⁻³ ) Couche d'InP suivie d'une couche de 0,2 µm dopé progressivement (passant de 1 × 10 ¹⁷ cm ⁻³ à 3 × 10 ¹⁷ cm ⁻³ ) Couche InP et un InP 0,5 µm (5 × 10 ¹⁸ cm ⁻³ ) la couche de contact a été réalisée en séquence en tant que gaine supérieure par épitaxie métal-organique en phase vapeur (MOVPE).

Après la mise en œuvre du motif de réseau et de la repousse, l'épi-wafer a été gravé en crêtes de 10 µm de large, puis les guides d'ondes ont été réintroduits dans le système MOVPE et enterrés dans du InP (Fe) semi-isolant. Un SiO₂ de 450 nm d'épaisseur La couche a été déposée par dépôt chimique en phase vapeur assisté par plasma (PECVD) pour l'isolation autour de la crête, et le contact électrique a été assuré par une couche de Ti/Au. Une couche d'or supplémentaire de 5 µm d'épaisseur a ensuite été électrodéposée pour améliorer encore la dissipation thermique. Les guides d'ondes ont été clivés en barres de 2 mm de long et les tests ont été effectués sur des dispositifs dotés de revêtements à facettes à réflectivité optimisée. Revêtement HR des deux faces arrière composé d'Al₂ O₃ /Ti/Au/Ti/Al₂ O₃ (400/5/100/10/200 nm) et le revêtement AR de la facette avant composé d'Al₂ O₃ /Ge (380/33 nm) sont déposés par évaporation par faisceau électronique. La réflectivité calculée de la facette avant est de 3,4% pour une longueur d'onde de 4,76 µm, et la relation détaillée entre la fluctuation de l'épaisseur du revêtement et la réflectivité a été discutée dans notre article publié précédemment [19]. Les lasers ont été montés côté épicouche vers le bas sur des dissipateurs thermiques SiC avec de la soudure à l'indium, puis reliés par fil à une plage de contact externe. Pour la caractérisation spectrale et électrique, les lasers sont montés sur un élément Peltier et la température a été surveillée sur le dissipateur thermique avec une thermistance.

Résultats et discussion

La figure 3 montre les spectres d'émission sous le seuil modifiés dynamiquement de l'électroluminescence au laser avec le courant croissant qui est mesuré avec le Bruker Vertex 70 FTIR et un détecteur HgCdTe refroidi à l'azote. Le spectre laser juste au-dessus du seuil indique que l'appareil fonctionne sur le mode fondamental et on peut clairement obtenir la bande d'arrêt du mode fondamental lorsque le courant est de 285 mA. À partir de la largeur de bande d'arrêt Δν = 3.076 cm ⁻¹ et l'indice effectif n _eff = 1/(2νΛ) = 3.153, on calcule un coefficient de couplage κ = Δν ·π ·n _eff = 30,4 cm ⁻¹ , résultant pour notre cavité de 2 mm de long revêtue HR dans un produit de couplage κL de 12,1, ce qui correspond bien à la fabrication de notre appareil. Le produit de κL beaucoup plus grand que l'enquête théorique précédente κL ≈ 1 [20] indique qu'un schéma de surcouplage est obtenu, ce qui est bénéfique pour sécuriser le mode unique dans toute la plage de température actuelle et examinée.

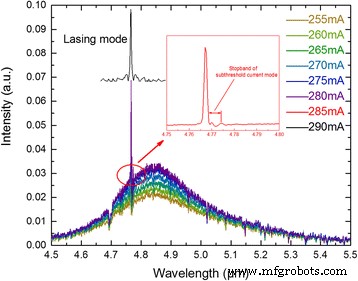
Spectre CC inférieur au seuil de l'appareil mesuré à 30 °C

La figure 4a montre la puissance-courant-tension CW typique (P -Je -V ) courbe du laser DFB à différentes températures de radiateur entre 20 et 90 °C. La puissance de sortie atteint 200 mW pour l'appareil de 2 mm de long avec une densité de courant de seuil bas de 0,65 kA/cm ² à 20 °C. La tension de seuil (V _ème ) de 13,2 à 14,2 V a été mesurée sur la plage de température de 20 à 90 °C. Il convient de noter que le saut de mode n'existe qu'à une température de dissipateur thermique inférieure à 60 °C, ce qui peut être facilement déduit du P -Je courbe. Une température élevée du dissipateur thermique contribuerait à une accumulation de chaleur plus importante dans le cœur du laser, de sorte que l'effet thermique restreindrait un autre mode laser et qu'un saut de mode ne se produirait pas. La figure 4b montre le P -Je -V courbe du laser DFB qu'un revêtement antireflet (AR) a été déposé sur sa facette avant, et nous choisissons une réflectivité du revêtement AR de 3,4%. Chaque P lisse -Je les courbes indiquent qu'il n'y a pas d'existence de saut de mode tout autour de la température que nous avons mesurée. La figure 4c, d montre le spectre laser à différents courants de 150 à 250 mA avec un pas de 25 mA. Il est évident à partir de la figure 4d que nous obtenons un mode unique stable autour de différents courants avec un revêtement de facette AR optimisé plutôt qu'un saut de mode sur la figure 4c. La fréquence garde toujours une relation linéaire avec le courant d'injection, et le coefficient d'accord actuel Δν /ΔJe = − 0,024 cm ⁻¹ mA ⁻¹ prouve que le revêtement AR est une méthode simple et efficace pour résoudre le problème du saut de mode dans les DFB-QCL.

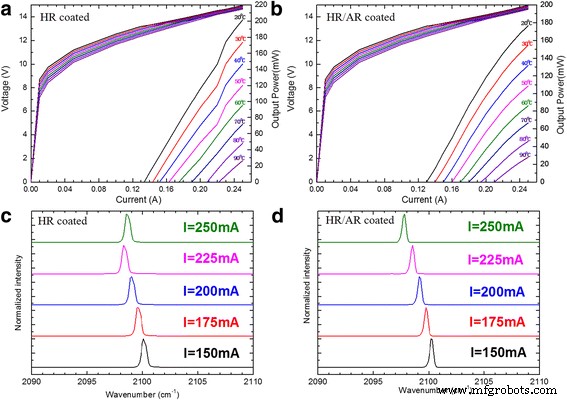
un , b Puissance de sortie en fonction du courant du laser DFB fonctionnant en mode CW à différentes températures de dissipateur thermique entre 20 et 90 °C avec V -Je courbes. c , d Spectres laser CW à différents courants de 150 à 250 mA avec un pas de 25 mA à 20 °C

La figure 5 montre les spectres d'émission du laser DFB de revêtement à différentes températures de dissipateur thermique de 20 à 90 °C. Les mesures ont été réalisées à l'aide d'un spectromètre FTIR NICOLET 8700 à 0,25 cm ⁻¹ résolution en mode de balayage rapide. Une émission de mode longitudinal unique est observée dans toute la plage de températures étudiée avec un rapport de suppression de mode latéral (SMSR) de 26 dB à haute température de 90 °C. Comme le montre l'encart de la figure 5, le spectre d'émission de crête a été observé pour passer de 2100,4 cm ⁻¹ à 20 °C à 2088,6 cm ⁻¹ à 90 °C, correspondant à un coefficient d'accord de température Δν /ΔT = − 0,168 cm ⁻¹ K ⁻¹ . Le bon réglage linéaire a indiqué qu'aucun saut de mode ne s'est produit pendant le changement de température du dissipateur thermique. De plus, tous les appareils mentionnés affichent un champ lointain latéral unique dominant en mode CW sur le mode fondamental en raison du contrôle précis de la largeur de la crête.

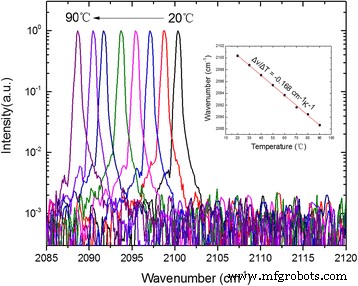
Spectres d'émission monomode du laser DFB à un courant de seuil de 1,1 pour différentes températures de dissipateur thermique de 20 à 90 °C. L'insert montre les caractéristiques de réglage linéairement ajustées de la fréquence laser avec la température

Le CW WPE a été calculé et tracé en fonction de la consommation électrique d'entrée sur la figure 6. À 20 °C, un WPE maximum de 4,7 % a été obtenu autour de 240 mA avec une puissance de sortie de 170 mW. Les WPE maximales étaient toujours de 2,9 et 0,8 % à 50 et 90 °C respectivement. À ce jour, ces valeurs étaient encore très élevées pour les DFB-QCL à bas seuil en raison de la haute qualité de nos matériaux et de notre revêtement de facettes à réflectivité optimisée. On pense que le WPE peut être encore amélioré par la sélection optimisée des longueurs de cavité laser compte tenu de l'effet de revêtement.

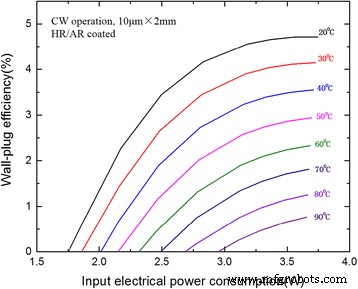
Rendement de la prise murale en fonction de la puissance électrique dissipée pour le DFB-QCL à revêtement AR et HR de 2 mm de long

Conclusions

Nous avons démontré le fonctionnement CW à température ambiante des DFB-QCL monomodes à λ ~ 4,76 m. En déposant un revêtement AR constitué de diélectrique double couche Al₂ O₃ et Ge sur la face avant, un mode unique stable sans aucun saut de mode dans toutes les conditions de courant et de température a été réalisé avec succès. À 20 °C, une puissance de sortie CW aussi élevée que 170 mW a été observée avec une densité de courant seuil très faible de 0,65 kA/cm ² . De tels dispositifs représentent une étape importante vers l'utilisation d'un fonctionnement monomode stable des DFB-QCL dans la plage spectrale de l'infrarouge moyen pour des applications pratiques.

Abréviations

AR :

Antireflet

BH :

Hétérostructure enterrée

CW :

Onde continue

DFB :

Commentaires distribués

RH :

Haute réflexion

MBE :

Epitaxie par faisceau moléculaire

MOVPE :

Epitaxie en phase vapeur organique métallique

PDE :

Equation aux dérivées partielles

PECVD :

Dépôt chimique en phase vapeur assisté par plasma

P -Je -V :

Puissance-courant-tension

QCL :

Laser à cascade quantique

SMSR :

Taux de suppression de mode latéral

V _ème :

Tension de seuil

WPE :

Efficacité de la prise murale

λ /4 PS :

Un déphasage quart d'onde