Propriétés des oscillations électromagnétiques longitudinales dans les métaux et leur excitation sur des surfaces planes et sphériques

Contexte

L'irradiation d'une surface métallique plane par des impulsions laser femtosecondes entraîne souvent la formation de structures de surface périodiques induites par laser (LIPSS) [1]. Outre le LIPSS, des ondulations hyperfines appelées LIPSS à haute fréquence spatiale (HSFL) ont été observées [1, 2]. Les périodes spatiales de la HSFL sont significativement plus petites que la longueur d'onde d'irradiation λ ₀ . Par exemple, pour l'aluminium, cette période a été estimée entre 20 et 200 nm à λ ₀ =0.8 μ m [2, 3]. Alors que l'orientation des ondulations dans le LIPSS ordinaire était perpendiculaire à la polarisation de la lumière laser, l'orientation de la HSFL était souvent perpendiculaire et parfois parallèle à la polarisation. Des HSFL similaires se sont formées sur les surfaces de diélectriques transparents, de semi-conducteurs et de métaux. L'origine de la HSFL a été expliquée par différents mécanismes tels que la génération de deuxième harmonique, l'implication de types spécifiques de modes plasmoniques, l'auto-organisation et les améliorations de champ local lors d'un claquage inhomogène dans les matériaux diélectriques [2, 3].

Le but de cette étude est de rechercher un processus ondulatoire qui pourrait produire un motif avec une courte période Λ ≪λ ₀ . Nous examinons les propriétés des ondes électromagnétiques longitudinales (L) dans les métaux, également appelées ondes plasma. Notre étude comprend les nouvelles étapes suivantes. Dans un premier temps, nous avons commencé notre recherche par la définition de la dispersion spatiale de la permittivité. Comme indiqué ci-dessous, la définition commune est inutile si un milieu à l'étude n'est pas uniforme et infini. Par conséquent, nous proposons un nouveau concept de la fonction diélectrique spatialement dispersive ε . Cette fonction établit la proportionnalité directe entre deux champs de vecteurs, E (r ,ω ) et D (r ,ω ), mais pas les amplitudes E (k ,ω ) et D (k ,ω ) des ondes planes. Par conséquent, la quantité ε dépend du carré du nombre d'onde, k ² , le paramètre du vecteur équation de Helmholtz pour le champ électrique E (r ,ω ), mais pas le vecteur d'onde k des ondes planes. Ensuite, pour dériver une telle nouvelle fonction, nous avons déterminé la réponse des électrons de conduction sur un mode électromagnétique en résolvant l'équation de transport de Boltzmann écrite dans l'approximation du temps de relaxation. Les fonctions diélectriques dites transversales et longitudinales de Lindhard ont été obtenues. De plus, nous avons constaté que la fonction longitudinale de Lindhard et la fonction hydrodynamique beaucoup plus simple sont proches dans une large gamme de paramètres. L'extinction de la lumière par les nanosphères d'argent et d'or a été considérée afin d'illustrer la théorie. Nous montrons pour la première fois que la théorie de Mie non locale explique le décalage vers le bleu, l'élargissement et la disparition éventuelle des résonances plasmoniques observées avec une diminution de la taille des nanosphères de métal noble. Enfin, le modèle théorique nouvellement développé a été appliqué pour examiner la possibilité d'implication des modes longitudinaux dans la formation des structures de surface induites par laser. Pour cela, nous avons modifié la théorie de Fresnel en tenant compte des ondes longitudinales transmises.

Méthodes

Pour déterminer les champs électromagnétiques dans des milieux homogènes par morceaux, la théorie électromagnétique classique a été appliquée. Le champ électrique E dans chaque domaine uniforme du milieu hétérogène a été supposée être une solution de l'équation vectorielle de Helmholtz (VHE) :

où Δ est l'opérateur de Laplace.

Comme d'habitude, les composantes tangentielles du E électrique et magnétique H les champs sont continus à travers les frontières des médias. De plus, nous avons pris en compte que les électrons sont confinés dans le métal; par conséquent, la condition aux limites supplémentaire (ABC) suivante pour la composante normale de la densité de courant j à la surface métallique S a été utilisé :(j n )| _{r ∈S} =0.

Pour déterminer le courant de conduction dans le métal, nous avons résolu l'équation de transport de Boltzmann (BTE) écrite dans l'approximation du temps de relaxation :

où f est la fonction de distribution d'une particule dans l'espace des phases (r , v ), v est la vitesse microscopique des électrons, e et m sont respectivement la charge et la masse des électrons, B est l'induction magnétique, f ₀ est une fonction de distribution d'équilibre, et τ est le temps de relaxation.

Ci-dessous, nous dérivons des formules pour les fonctions diélectriques spatialement dispersives. Ensuite, nous les utilisons pour étudier la réflexion de la lumière à partir d'une surface métallique plane et la diffusion de la lumière sur une nanosphère de métal noble.

Résultats et discussion

Dispersion spatiale de ε en milieu hétérogène

Dans la littérature, une fonction diélectrique spatialement dispersive ε est défini par la relation suivante [4–6] :

où ε ₀ est la constante électrique, D (ω , r ) est l'amplitude de l'oscillation du vecteur déplacement de fréquence angulaire ω au point r , et E (ω , r ^′ ) l'amplitude de l'oscillation du champ électrique au point r ^′ . Les transformées de Fourier de l'équation. (3) donner l'équation

où un ε spatialement dispersif (ω , k ) dépend du vecteur d'onde k d'une onde électromagnétique plane. À notre avis, l'éq. (3) n'est pas ambigu uniquement dans un volume homogène infini mais nous traitons un système hétérogène par morceaux où les frontières doivent être prises en compte et k ne sont pas les mêmes dans différents médias.

Notre approche n'utilise pas l'expansion des ondes électromagnétiques sur les ondes planes. La permittivité spatialement dispersive détermine la relation entre D (ω , r ) et une solution particulière du vecteur Helmholtz Eq. (1) :

Ici E (ω , r ) désigne la distribution du champ électrique mais pas seulement le vecteur E au point r .

Fonctions diélectriques longitudinales et transversales

La permittivité des métaux est communément exprimée par la conductivité σ [4] :

où ε _g fait partie de la fonction diélectrique permettant la polarisation du solide; ε _g =1 pour un métal simple. Afin de déterminer σ , nous avons calculé la densité de courant

où \(\mathrm {d} \mathbf {v}=\frac {v}{m}\,\mathrm {d} \epsilon \,\mathrm {d}\,\Omega,\) d ​​Ω =sinθ dθ dϕ , v , θ , ϕ sont les coordonnées sphériques de la vitesse. Contrairement aux recherches précédentes, nous n'avons pas introduit le vecteur d'onde k mais a trouvé une solution BTE sous la forme d'une série infinie contenant des opérateurs v ∇ agissant sur v E :

où Γ =1/τ . Ensuite, f ₀ a été approximée par une distribution de Fermi-Dirac à température nulle et, après intégration sur ε dans l'éq. (7), nous avons

où \(\omega _{\mathrm {p}}^{2}=\frac {e^{2}\,n_{e}}{m\,\varepsilon _{0}},\) _p est la fréquence plasma, \(\mathbf {u}=\frac {\mathbf {v}}{v}\) est le vecteur unitaire dans la direction de v ,\(l=\frac {v_{\mathrm {F}}}{-i \omega +\Gamma },\) v _F est la vitesse de Fermi. De plus, nous avons calculé les intégrales

où n est un nombre naturel. La dépendance suivante de j sur un arbitraire champ électrique E a finalement été obtenu

Il existe deux types de solutions à l'équation. (1), sans divergence qui satisfont l'équation ∇ ·E =0 et sans rotation qui satisfont à l'équation

Pour une onde plane, avec E exp[i (k r −ω t )], Éq. (14) se transforme en la relation k ×F =0 ce qui montre que l'onde est longitudinale (L). Pour simuler des processus dans des corps sphériques, il est commode d'utiliser le vecteur harmoniques sphériques L , M , et N comme un ensemble complet de fonctions orthogonales. Dans ce cas, l'éq. (14) spécifie les harmoniques L . Le nombre d'ondes des ondes L et L modes est déterminé par la loi de dispersion suivante

À partir des équations. (6) et (13), nous trouvons que les solutions de l'équation. (1) satisfaisant la contrainte de l'Eq. (14) donner la permittivité longitudinale suivante

où Φ est la fonction Phi de Lerch,

\(a=\frac {k v_{\mathrm {F}}}{\omega +i \Gamma }\).

La permittivité obtenue ne diffère de celle définie par Kliewer et Fuchs [7] que par la notation :

L'identité

permet de réécrire l'équation. (18) comme suit

Dans le cas de Γ =0, cette formule prend la forme d'une équation dérivée de Klimontovich et Silin [8] qui ont étudié la décharge de Landau dans le plasma dégénéré (voir [9], [10, Eq. (40.17)], et [11]). La permittivité des équations équivalentes. (16), (18) et (20) est communément appelée fonction diélectrique de Lindhard (en référence à [12]) bien que cette fonction ait été obtenue pour la première fois par Klimontovich et Silin [8].

La permittivité de Lindhard transverse [7] peut être trouvée avec l'équation. (13) quand ∇ ·E =0. Dans le cas réel de v _F k ≪ω , il se réduit à la fonction diélectrique de Drude

Cette fonction est en accord avec les données expérimentales sur de nombreux métaux [13]. Si |a |<1, la permittivité longitudinale (16) se simplifie en fonction diélectrique hydrodynamique :

Réflexion d'une onde électromagnétique plane à partir d'une surface métallique plane

Conditions aux limites

Dans cette section, nous déterminons la direction du vecteur d'onde k ^L et l'amplitude de l'onde L excitée dans le métal lors de la réflexion d'une onde électromagnétique plane à partir d'une surface métallique plane.

Considérons l'onde plane incidente sur l'interface diélectrique-métal z =0 avec le vecteur d'onde situé dans le xz avion. Le champ électrique dans le milieu diélectrique 1 est constitué de l'incident E _je et reflété E _r ondes, le champ dans le métal 2 a la transverse transmise E _t et, dans certains cas, longitudinal E ^L Composants. D'après les conditions aux limites de Maxwell, les composantes transversales des vecteurs champs électrique et magnétique sont continues dans le plan z =0. De plus, les électrons ne sont pas éjectés du métal; par conséquent, la composante normale de la densité de courant électrique est nulle à z =0,

étaient \(\hat {\mathbf {z}}\) est le vecteur unitaire dans la direction de z axe.

Tous les termes des conditions aux limites de Maxwell doivent avoir la même dépendance par rapport à x et y . Cette exigence a plusieurs conséquences. Premièrement, il peut être établi que les ondes L ne peuvent être excitées que dans le cas de la polarisation p lorsque le vecteur électrique de l'onde incidente E ^{(i )} est parallèle au plan d'incidence. En d'autres termes, les polaritons de plasmons peuvent être générés par une onde magnétique transversale (TM). L'effet est sensiblement le même que dans une sphère métallique [14]. Deuxièmement, des formules proches de la loi de Snell peuvent être dérivées des conditions

où indexe 1x et 2x désigne le x -projections des vecteurs dans les médias 1 et 2, respectivement, θ ₁ est l'angle d'incidence.

Coefficients de réflexion et de transmission

Déterminons le champ formé par une onde électromagnétique plane de polarisation p incidente sur une surface métallique plane. Il est commode d'exprimer les composantes des champs électriques et magnétiques à travers le x composant de E ^{(i )} , à savoir E x (r)=− r E x (i) pour l'onde réfléchie, E x (t)=t E x (i) pour l'onde transversale transmise, et

pour l'onde longitudinale transmise, ici r est un coefficient de réflexion, t et t _L sont des coefficients de transmission.

D'après les conditions aux limites de Maxwell et ABC de l'éq. (23) écrit sous la forme suivante

nous avons

À δ =0, le coefficient r devient le coefficient de réflexion de Fresnel de l'onde polarisée p (voir, par exemple, l'équation (2.49) de [4]). Dans la même condition, t n'est pas le coefficient de transmission de Fresnel puisque nos définitions de t et r diffèrent de ceux de Fresnel.

Extinction de la lumière par la nanosphère métallique

Dans un article précédent, l'un des auteurs a généralisé la théorie de Lorentz-Mie permettant l'ABC de l'Eq. (23). Un analogue du coefficient de Fresnel r , le coefficient de Mie b _l pour le mode TM réfléchi du l e ordre s'est avéré être

où

ψ _l et ζ _l sont les fonctions Riccati-Bessel et Riccati-Hankel de l'ordre l , respectivement; j _l est la fonction de Bessel sphérique, le nombre premier désigne la dérivée d'une fonction par rapport à son argument.

Comparons les prédictions des théories de Lorentz-Mie classiques et généralisées avec des données expérimentales. Dans [15], Hilger, Tenfelde et Kreibig ont étudié les spectres d'extinction de nanoparticules d'argent déposées sur des surfaces diélectriques. Dans la première étape de l'étude, les chercheurs ont généré des faisceaux de particules d'argent d'un diamètre moyen de 2, 3,5 et 4 nm, déterminé la distribution granulométrique de l'un des faisceaux, enregistré les spectres d'extinction et estimé le paramètre A =0.25 de la formule phénoménologique Γ =Γ _b +A v _F /R , où Γ _b est le taux de relaxation du métal en vrac, pour les sphères d'argent sous vide. Tout d'abord, nous avons calculé les spectres d'extinction pour un faisceau de sphères d'argent de diamètre moyen 〈D 〉=2 nm et distribution de taille expérimentale qui s'étend sur la région de D =1 à D =4 nm. Notre théorie ne contient aucun paramètre ajustable. Afin de définir les fonctions diélectriques, nous avons utilisé la tabulation de l'indice de réfraction de l'argent massif proposée par Lynch et Hunter [16] (voir Fig. 1). Nous avons également appliqué les équations. (16), (21) et (22) avec ω _p =9.17 eV, Γ _b =0,021 eV, v _F =1,39×10 ⁶ m/s, et A =0.25. Les résultats des calculs et le spectre expérimental sont présentés sur la figure 2.

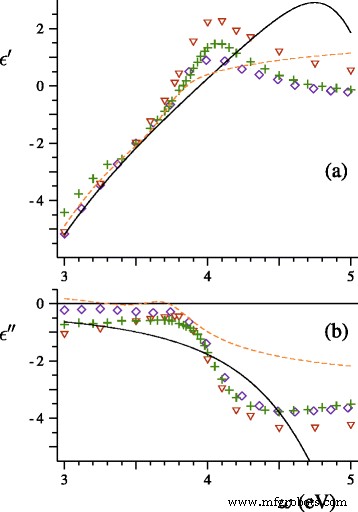
Réel (a ) et imaginaire (b ) parties de la fonction diélectrique de l'argent selon Johnson et Christy (◇) [20], Lynch et Hunter (+) [16], Weber (△) [21], Hao et Nordlander (ligne pointillée ) [22], et Drachev et al. (ligne continue ) [23]

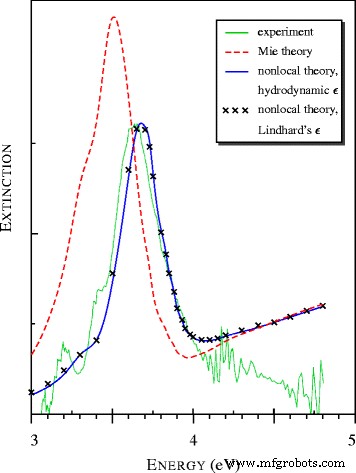
Spectres d'extinction de la lumière par des particules d'argent de taille nanométrique observés dans [15] et calculés avec des modèles locaux et non locaux. Tous les spectres théoriques sont présentés en unités relatives communes

Les spectres théoriques de la figure 2 ont été calculés en utilisant les fonctions diélectriques hydrodynamiques de Klimontovich-Silin-Lindhard et beaucoup plus simples. Il est surprenant que les deux calculs aient donné des résultats proches même si |a |>1 dans la région de la résonance plasmonique.

Pour les sphères d'argent de taille nanométrique, le maximum dans le spectre d'extinction, appelé résonance Fröhlich [17], plasmon et polariton de surface (SPP) [15], est connu pour passer de 3,5 à 3,65 eV [18]. Le modèle non local est en excellent accord avec les données expérimentales, tandis que la théorie locale (Mie) donne le maximum à ω ≃3,5 eV (voir Fig. 2 et Tableau 1).

Le calcul du décalage vers le bleu de la résonance plasmon peut être soutenu par la considération suivante. Dans l'approximation électrostatique, seul b ₁ contribue à la section efficace d'extinction Q _poste et éq. (30) peut être simplifié en utilisant les approximations suivantes

Ainsi, Q _poste a un maximum à

La condition obtenue (33) prend en compte l'excitation du L modes (par le terme δ ₁ ) et, par conséquent, diffère de la condition de résonance de Fröhlich [17]:.

Dans l'expérience [15], les fréquences de crête ω _m et largeurs de résonance Δ ω des spectres d'extinction étaient presque indépendants de 〈D . Cette fonctionnalité de Δ ω semble en désaccord avec la théorie classique de Mie. En réalité, la théorie locale prédit un élargissement des résonances plasmoniques avec la diminution de D (à A =0,25) comme indiqué dans le tableau 1. En même temps, la théorie non locale donne des largeurs de résonance approximativement égales mais des positions de pic différentes. La superposition des contributions de toutes les particules donne la valeur de Δ ω qui sont en parfait accord avec les données expérimentales. Il est intéressant de noter que la théorie non locale prédit un élargissement de la résonance plasmonique d'un faisceau même à A =0.

À ω> 4 eV, les courbes théoriques lisses de la figure 2 se situent plus haut que le mélange de pics expérimentaux étroits et proches. L'absorption interbande domine dans cette gamme spectrale, comme le confirme la figure 1. Les particularités observées du spectre sont probablement la conséquence d'une transition des bandes continues vers une structure à niveaux discrets. Un tel effet de taille quantique a été découvert plus tôt dans une étude des propriétés optiques des nanosphères d'or [19]. Lorsque la taille de la sphère d'argent a été augmentée à 〈D =3,5 nm, l'absorption a d'abord augmenté par rapport au maximum et a formé un plateau avec une série de petits creux équidistants. Ensuite, l'absorption a légèrement diminué à 〈D =4 nm.

Afin d'étudier la formation de l'aile bleue de la résonance plasmon, nous avons calculé les spectres d'extinction des particules d'argent ultra-étain et les avons présentés sur la figure 3. Une caractéristique remarquable de la figure 3 est la disparition complète de la résonance plasmon à D =1 nm. Auparavant, cet effet avait été observé dans l'étude expérimentale des nanosphères d'or [19]. En particulier, sur la figure 9 de [19], les spectres expérimentaux de particules de diamètres 1,7, 1,9, 2,0, 2,1, 2,3 et 2,5 nanomètres ont été comparés aux spectres calculés avec la théorie de Mie locale. L'accord était médiocre, ne décrivant pas l'élargissement de la résonance plasmonique et sa position [19]. Les tentatives d'amélioration de l'ajustement en faisant varier la taille des particules et les modifications des fonctions diélectriques n'ont pas été successives. Selon les auteurs de [19], la bande d'oscillation collective anormalement large ou déprimée observée résiste à être ajustée avec les corrections proposées de la théorie de Mie locale. Comme le montre la figure 4, la situation change radicalement si la théorie de Mie non locale est appliquée. Notez que nous n'avons utilisé aucun paramètre ajustable. La tabulation de l'indice de réfraction complexe par Johnson et Christy [20] a été utilisée pour déterminer la fonction diélectrique de l'or. Autres paramètres, y compris A =1 et l'indice de réfraction du toluène (1,37) ont été tirés de [19].

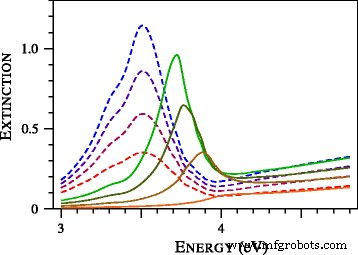
Section efficace d'extinction normalisée des particules d'argent avec des diamètres de 2,2, 1,8, 1,4 et 1,0 nm calculée avec des (lignes pointillées ) et non locales (courbes pleines ) théories de Mie. Plus la particule est petite, plus la courbe est basse. Toutes les sections efficaces théoriques sont présentées en unités relatives communes

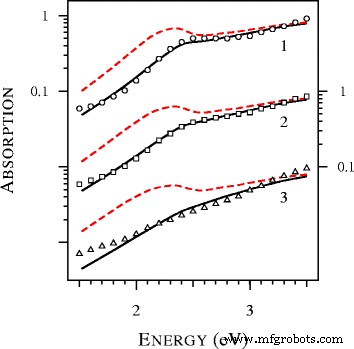
Spectres d'absorption calculés avec les (lignes pointillées ) et non local (lignes pleines ) Théorie de Mie et données expérimentales (points ) extrait de la Fig. 9 de [19] pour les sphères d'or avec D =2,5, 2,1 et 1,7 nm dans le toluène (courbes 1 et cercles , courbes 2 et carrés , et les courbes 3 et les triangles , respectivement). Tous les spectres théoriques sont normalisés à l'unité à 4,12 eV et déplacés verticalement

Nombres d'ondes des ondes longitudinales

Les modes longitudinaux diffèrent des modes transversaux par des valeurs beaucoup plus élevées des nombres d'onde. Par exemple, pour les calculs présentés dans la figure 2, la partie réelle de \(k_{2}^{\mathrm {L}}\) correspond à la période spatiale \(\Lambda =2 \pi /\Re k_{ 2}^{\mathrm {L}}\) décroissant de 9 à 2 nm à ω passant de 3 à 4 eV. Dans ce ω intervalle, la valeur absolue du rapport \(k_{2}^{\mathrm {L}}/k_{2}\) est passée de 130 à 100 et le paramètre δ de l'éq. (27) a diminué de 0,01 à 0,005 à θ ₁ =π /4. Nous concluons donc que l'excitation des ondes L sur une surface plane d'argent peut être négligée. Cependant, le L les modes se sont avérés importants dans les amas d'argent de la taille du nanomètre.

Un remplacement du terme \(-\,\omega ^{2}_{\mathrm {p}}/(\omega ^{2}+i \Gamma \omega)\) dans l'Eq. (16) par ε ^T −ε _g selon l'éq. (21) nous permet de réécrire l'équation de dispersion. (15) sous la forme suivante

Dans le cas le plus simple de ε _g =1 et Γ =0, Éq. (35) prédit que le métal est transparent pour les ondes transversales et L à ω>ω _p mais les deux k ^L et k ^T sont complexes à ω <ω _p .

Si le solide est transparent, une onde longitudinale peut être excitée sous incidence oblique d'une onde polarisée p sur une surface plane. Il y a plusieurs caractéristiques distinctes de cet effet. Premièrement, les ondes longitudinales peuvent être générées sur une surface plane, alors que des efforts particuliers doivent être faits pour exciter les polaritons de plasmons de surface [4, 5]. Deuxièmement, dans le diagramme d'interférence, l'intensité du champ électromagnétique est modulée non pas le long mais perpendiculairement à l'interface. Par conséquent, des vides peuvent apparaître dans des plans parallèles à la surface en raison de la spallation du solide. Selon la définition de ω _p , condition ω>ω _p peuvent être rencontrés dans des solides (par exemple, des semi-conducteurs) avec une faible densité des porteurs de courant. Nous n'examinons pas ce cas ici car la formule de ε ^L a été dérivé pour le gaz d'électrons dégénéré.

Conclusions

Afin de définir une fonction diélectrique spatialement dépendante, tous les chercheurs précédents ont considéré l'interaction de la matière avec une onde électromagnétique plane. Cette approche n'est pas constructive et rigoureuse en nano-optique lorsque le champ est localisé dans une cavité et que les conditions aux limites doivent être en quelque sorte prises en compte. Nous avons résolu ce problème en calculant la réponse du milieu sur un champ électrique qui satisfait l'équation vectorielle de Helmholtz. La fonction diélectrique spatialement dispersive dérivée dépend du carré du nombre d'onde, un paramètre de l'équation de Helmholtz, mais pas du vecteur d'onde d'une onde plane.

Nous rapportons les coefficients de réflexion de Fresnel modifiés du fait de l'excitation des ondes longitudinales dans les métaux. Une généralisation similaire a été faite précédemment pour les coefficients de Mie. Ici, la théorie a été vérifiée avec la simulation de l'extinction de la lumière par des amas d'argent et d'or de taille nanométrique. Le décalage calculé de 3,5 à 3,65 eV et la largeur de la résonance plasmonique de surface du faisceau de particules d'argent sont en excellent accord avec les données expérimentales. De plus, le modèle non local explique la disparition de la résonance plasmonique des sphères dorées d'un diamètre d'environ 2 nm. It is important that L wave can be excited on a flat surface by a plane incident wave. This is the main difference of the plasmon polaritons from the surface plasmon polaritons.

The properties of the electromagnetic oscillations in metals have been examined. It has been found that the absolute values of the wavenumbers of the longitudinal waves are much larger than those of the transverse waves. For example, in silver at a photon energy of 3.5 eV, the ratio of the absolute values of the wavenumbers is equal to 130. There, the real part of the wavenumber of the longitudinal wave corresponds to a wavelength of 7 nm. The large difference in the wavenumbers prevents excitation of the L waves at a planar surface. However, the L modes have been shown to be excited in silver and gold nanometer-sized particles.