Loi de courant et de tension de Kirchhoff (KCL &KVL) | Exemple résolu

KCL et KVL – Première et deuxième lois de Kirchhoff avec exemple résolu

Un physicien allemand "Robert Kirchhoff" a introduit deux lois électriques importantes en 1847 grâce auxquelles nous pouvons facilement trouver la résistance équivalente d'un réseau complexe et des courants circulant dans différents conducteurs. Les circuits AC et DC peuvent être résolus et simplifiés en utilisant ces lois simples connues sous le nom de loi du courant de Kirchhoff (KCL) et loi de tension de Kirchhoff (KVL).

Notez également que KCL est dérivé de l'équation de continuité de charge en électromagnétisme tandis que KVL est dérivé de l'équation de Maxwell - Faraday pour le champ magnétique statique (la dérivée de B par rapport au temps est 0 ).

Loi actuelle de Kirchhoff (KCL) :

Selon KCL :

Dans tout réseau électrique, la somme algébrique des courants entrants vers un point et des courants sortants à partir de ce point est nulle. Soit les courants entrants en un point sont égaux aux courants sortants de ce point.

En d'autres termes, la somme des courants circulant vers un point est égale à la somme de ceux qui s'en éloignent. Soit la somme algébrique des courants entrant dans un nœud est égale à la somme algébrique des courants qui en sortent.

Explication de KCL :

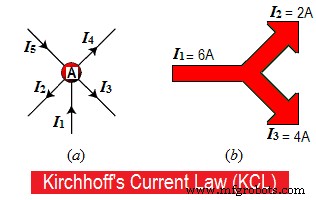
Supposons que certains conducteurs se rencontrent en un point « A », comme le montre la figure 1.a. Dans certains conducteurs, les courants arrivent au point "A" tandis que dans d'autres conducteurs, les courants partent ou sortent du point "A".

Je ₁ + (–je ₂ ) + (–je ₃ ) + (–je ₄ ) + je ₅ =0

OU

Je ₁ + je ₅ – je ₂ – je ₃ – je ₄ =0

OU

Je ₁ + je ₅ =je ₂ + je ₃ + je ₄ =0

c'est-à-dire

Courants entrants ou entrants =Courants sortants ou sortants

Ou

Σje Saisie =ΣI Partir

Par exemple, 8A se dirige vers un point et 5A plus 3A quittent ce point sur la figure 1.b, donc,

8A =5A + 3A

8A =8A.

Loi de tension de Kirchhoff (KVL) :

La deuxième loi de Kirchhoff ou KVL stipulait que ;

En d'autres termes, dans toute boucle fermée (également appelée maillage), la somme algébrique de la FEM appliquée est égale à la somme algébrique des chutes de tension dans les éléments . La deuxième loi de Kirchhoff est également connue sous le nom de loi de tension ou loi de maillage.

ΣIR=ΣE

Explication de KVL :

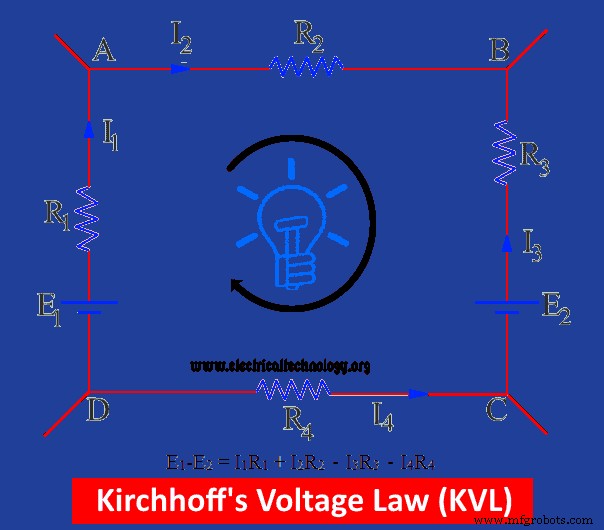
Un circuit fermé est représenté sur la figure qui contient deux connexions de batteries E₁ et E₂ . La somme globale des E.M.F des batteries est indiquée par E₁ -E₂ . La direction imaginaire du courant est également indiquée sur la figure.

E₁ entraîne le courant dans une telle direction qui est supposée être positive tandis que E₂ interfère dans la direction du courant (c'est-à-dire qu'elle est dans la direction opposée à la direction supposée du courant) par conséquent, elle est considérée comme négative. La chute de tension dans ce circuit fermé dépend du produit de la tension et du courant.

La chute de tension se produit dans la direction supposée du courant est connue sous le nom de chute de tension positive tandis que l'autre est une chute de tension négative.

Dans la figure ci-dessus, I₁ R₁ et moi₂ R₂ sont des chutes de tension positives et I₃ R₃ et moi₄ R₄ sont négatifs V.D.

Si nous faisons le tour du circuit fermé (ou de chaque maille) et que nous multiplions la résistance du conducteur et le courant qui y circule, alors la somme de l'IR est égale à la somme des sources EMF appliquées connectées au circuit.

L'équation globale pour le circuit ci-dessus est :

E₁ – E₂ =je ₁ R₁ + je ₂ R₂ – je ₃ R₃ – je ₄ R₄

Si nous allons dans la direction supposée du courant comme indiqué sur la figure, alors le produit de l'IR est considéré comme positif sinon négatif.

Bon à savoir :

Direction du courant :

Il est très important de déterminer la direction du courant lors de la résolution de circuits via les lois de Kirchhoff. Idem dans le cas du courant électoral et du courant conventionnel.

La direction du courant peut être supposée dans le sens des aiguilles d'une montre ou dans le sens inverse des aiguilles d'une montre. Une fois que vous avez sélectionné la direction personnalisée du courant, vous devrez appliquer et maintenir la même direction pour l'ensemble du circuit jusqu'à la solution finale du circuit.

Si nous obtenons la valeur finale comme positive, cela signifie que la direction supposée du courant était correcte. En cas de valeurs négatives, le courant de la direction est alors inversé par rapport à celui supposé.

Analyse des circuits par les lois de Kirchhoff

Exemple résolu sur KCL et KVL (lois de Kirchhoff)

Exemple :

Résistances de R₁ =10Ω, R₂ =4 Ω et R₃ =8Ω sont connectés jusqu'à deux batteries (de résistance négligeable) comme indiqué. Trouvez le courant à travers chaque résistance.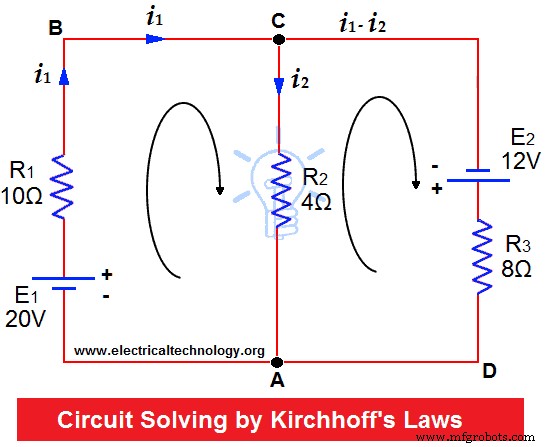

Solution :

Supposer que les courants circulent dans les directions indiquées par des flèches.

Appliquer KCL sur les jonctions C et A.

Par conséquent, courant dans le maillage ABC =i ₁

Courant dans Mesh CA =i ₂

Alors courant dans Mesh CDA =i ₁ – je ₂

Maintenant, appliquez KVL sur le maillage ABC, 20 V agissent dans le sens des aiguilles d'une montre. En égalant la somme des produits IR, nous obtenons ;

10i ₁ + 4i ₂ =20   …   (1)

Dans un ACD maillé, 12 volts agissent dans le sens des aiguilles d'une montre, alors :

8(i ₁ – je ₂ ) – 4i ₂ =12

8i ₁ – 8i ₂ – 4i ₂ =12

8i ₁ – 12i ₂ =12   …   (2)

Multiplier l'équation (1) par 3 ;

30i ₁ + 12i ₂ =60

Résoudre pour i ₁

30i ₁ + 12i ₂ =60

8i ₁ – 12i ₂ =12

___________
38i ₁ =72

L'équation ci-dessus peut également être simplifiée par l'élimination ou la règle de Cramer.

je ₁ =72 ÷ 38 =1.895 Ampères =Courant dans une résistance de 10 Ohms

En substituant cette valeur dans (1), nous obtenons :

10 (1,895) + 4i ₂ =20

4i ₂ =20 – 18,95

je ₂ =0,263 Ampère =Courant en résistances de 4 Ohms.

Maintenant,

je ₁ – je ₂ =1,895 – 0,263 =1,632 Ampères

Applications des lois de Kirchhoff

• Les lois de Kirchhoff peuvent être utilisées pour déterminer les valeurs de valeurs inconnues comme le courant et la tension ainsi que la direction des valeurs circulant de ces quintettes dans le circuit.
• Ces lois peuvent être appliquées sur n'importe quel circuit* (Voir la limitation des lois de Kirchhoff à la fin de l'article), mais utiles pour trouver les valeurs inconnues dans les circuits et réseaux complexes.
• Également utilisé dans l'analyse Nodal et Mesh pour trouver les valeurs de courant et de tension.
• Le courant à travers chaque boucle indépendante est transporté en appliquant KVL (chaque boucle) et le courant dans n'importe quel élément d'un circuit en comptant tout le courant (applicable dans la méthode du courant de boucle).
• Le courant à travers chaque branche est transporté en appliquant KCL (chaque jonction) KVL dans chaque boucle d'un circuit (applicable dans la méthode du courant de boucle).
• Les lois de Kirchhoff sont utiles pour comprendre le transfert d'énergie à travers un circuit électrique.

Bon à savoir :

Ces règles empiriques doivent être prises en compte lors de la simplification et de l'analyse des circuits électriques par les lois de Kirchhoff :

• La chute de tension dans une boucle due au courant dans le sens des aiguilles d'une montre est considérée comme une chute de tension positive (+).
• La chute de tension dans une boucle due au courant dans le sens inverse des aiguilles d'une montre est considérée comme une chute de tension négative (-).
• Le courant dérivé par la batterie dans le sens des aiguilles d'une montre est considéré comme positif (+).
• Le courant dérivé par la batterie dans le sens inverse des aiguilles d'une montre est considéré comme positif (-).

Limites des lois de Kirchhoff :

• KCL est applicable en supposant que le courant ne circule que dans les conducteurs et les fils. Alors que dans les circuits haute fréquence où, la capacité parasite ne peut plus être ignorée. Dans de tels cas, le courant peut circuler dans un circuit ouvert car dans ces cas, les conducteurs ou les fils agissent comme des lignes de transmission.
• KVL est applicable en supposant qu'il n'y a pas de champ magnétique fluctuant reliant la boucle fermée. Alors qu'en présence d'un champ magnétique changeant dans un circuit alternatif à haute fréquence mais à courte longueur d'onde, le champ électrique n'est pas un champ vectoriel conservateur. Ainsi, le champ électrique ne peut être le gradient d'aucun potentiel et l'intégrale linéaire du champ électrique autour de la boucle n'est pas nulle, ce qui contredit directement KVL. C'est pourquoi KVL n'est pas applicable dans une telle condition.
• Pendant le transfert d'énergie du champ magnétique au champ électrique où le fudge doit être introduit dans le KVL pour rendre le P.d (différences de potentiel) autour du circuit égal à 0.

Messages connexes sur les théorèmes d'analyse des circuits électriques :

• Théorème de Thevenin. Procédure étape par étape avec exemple résolu
• Théorème de Norton. Procédure facile étape par étape avec exemple (vues illustrées)
• Analyse de circuit SUPERNODE | Pas à pas avec un exemple résolu
• Analyse de circuit SUPERMESH | Pas à pas avec un exemple résolu
• Théorème de transfert de puissance maximale pour les circuits AC et DC
• Théorème de compensation – Preuve, explication et exemples résolus
• Théorème de substitution – Guide étape par étape avec exemple résolu
• Théorème de Millman – Analyse des circuits CA et CC – Exemples
• Théorème de superposition - Analyse de circuit avec exemple résolu
• Théorème de Tellegen – Exemples résolus et simulation MATLAB
• Règle du diviseur de tension (VDR) – Exemples résolus pour les circuits R, L et C
• Règle du diviseur de courant (CDR) – Exemples résolus pour les circuits CA et CC
• Loi d'Ohm :explication simple avec énoncé et formules
• Conversion étoile à delta et delta à étoile. Transformation Y-Δ