Inductance mutuelle et fonctionnement de base
Comportements des inducteurs enroulés autour d'un noyau conducteur
Supposons que nous devions enrouler une bobine de fil isolé autour d'une boucle de matériau ferromagnétique et alimenter cette bobine avec une source de tension alternative :(Figure ci-dessous (a))

L'enroulement isolé sur la boucle ferromagnétique a une réactance inductive, limitant le courant alternatif
En tant qu'inducteur, nous nous attendrions à ce que cette bobine à noyau de fer s'oppose à la tension appliquée avec sa réactance inductive, limitant le courant à travers la bobine comme prédit par les équations :
XL =2πfL et I=E/X (ou I=E/Z)
Pour les besoins de cet exemple, cependant, nous devons examiner plus en détail les interactions de la tension, du courant et du flux magnétique dans l'appareil.
La loi de tension de Kirchhoff décrit comment la somme algébrique de toutes les tensions dans une boucle doit être égale à zéro. Dans cet exemple, nous pourrions appliquer cette loi fondamentale de l'électricité pour décrire les tensions respectives de la source et de la bobine d'inductance.
Ici, comme dans tout circuit à une source et à une charge, la chute de tension à travers la charge doit être égale à la tension fournie par la source, en supposant une chute de tension nulle avec la résistance de tous les fils de connexion.
En d'autres termes, la charge (bobine d'induction) doit produire une tension opposée d'amplitude égale à la source, afin qu'elle puisse s'équilibrer par rapport à la tension source et produire une somme de tension de boucle algébrique de zéro.
D'où provient cette tension opposée ? Si la charge était une résistance (figure ci-dessus (b)), la chute de tension provient de la perte d'énergie électrique, le « frottement » des porteurs de charge circulant à travers la résistance.
Avec une inductance parfaite (pas de résistance dans le fil de la bobine), la tension opposée provient d'un autre mécanisme :la réaction à un flux magnétique changeant dans le noyau de fer. Lorsque le courant alternatif change, le flux Φ change. Changer de flux induit un compteur EMF.
Relation entre la tension, le courant et le flux magnétique
Michael Faraday a découvert la relation mathématique entre le flux magnétique (Φ) et la tension induite avec cette équation :

La tension instantanée (la chute de tension à tout instant) à travers une bobine de fil est égale au nombre de tours de cette bobine autour du noyau (N) multiplié par le taux de variation instantané du flux magnétique (dΦ/dt) reliant avec la bobine.
Graphiquement (figure ci-dessous), cela se présente sous la forme d'un ensemble d'ondes sinusoïdales (en supposant une source de tension sinusoïdale), l'onde de flux à 90° derrière l'onde de tension :
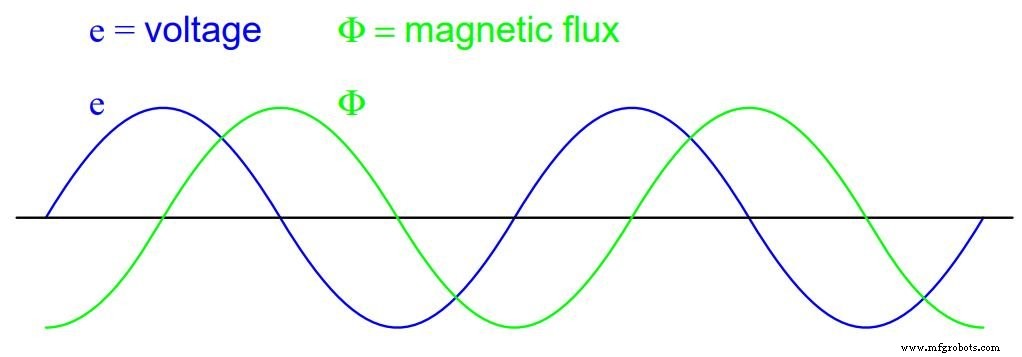
Le flux magnétique, comme le courant, retarde la tension appliquée de 90°
C'est pourquoi le courant alternatif à travers une inductance est en retard de 90° sur la forme d'onde de la tension appliquée :car c'est ce qui est nécessaire pour produire un flux magnétique changeant dont le taux de variation produit une tension opposée en phase avec la tension appliquée.
En raison de sa fonction de fournir une force magnétisante (mmf) pour le noyau, ce courant est parfois appelé courant magnétisant .
Il convient de mentionner que le courant traversant un inducteur à noyau de fer n'est pas parfaitement sinusoïdal (forme d'onde sinusoïdale), en raison de la courbe de magnétisation B/H non linéaire du fer.
En fait, si l'inducteur est construit à moindre coût, en utilisant le moins de fer possible, la densité de flux magnétique peut atteindre des niveaux élevés (approchant de la saturation), ce qui entraîne une forme d'onde de courant magnétisant qui ressemble à la figure ci-dessous :
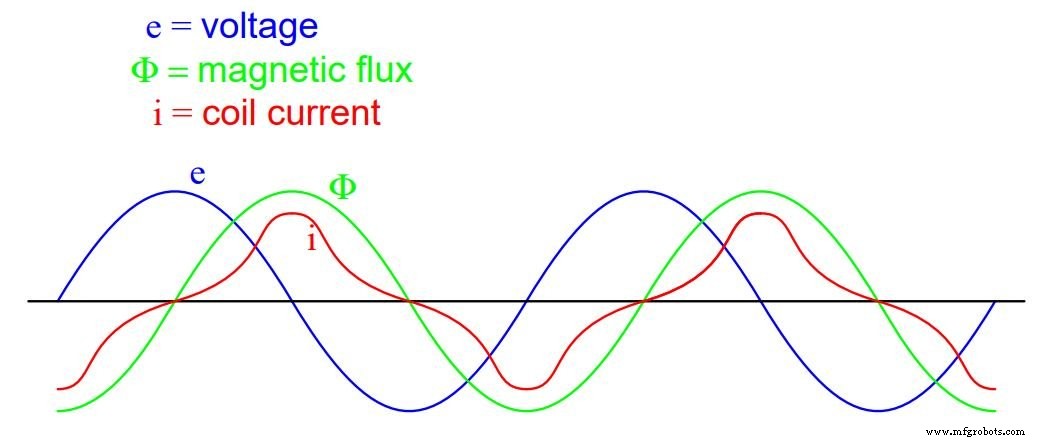
À mesure que la densité de flux approche de la saturation, la forme d'onde du courant magnétisant se déforme
Lorsqu'un matériau ferromagnétique approche de la saturation du flux magnétique, des niveaux disproportionnellement plus élevés de force de champ magnétique (mmf) sont nécessaires pour fournir des augmentations égales du flux de champ magnétique (Φ).
Parce que mmf est proportionnel au courant traversant la bobine magnétisante (mmf =NI, où "N" est le nombre de tours de fil dans la bobine et "I" est le courant qui la traverse), les grandes augmentations de mmf nécessaires pour fournir le nécessaire les augmentations de flux entraînent de fortes augmentations du courant de la bobine.
Ainsi, le courant de la bobine augmente considérablement aux pics afin de maintenir une forme d'onde de flux qui n'est pas déformée, ce qui représente les demi-cycles en forme de cloche de la forme d'onde de courant dans le tracé ci-dessus.
Courant excitant et ses effets
La situation est encore compliquée par les pertes d'énergie au sein du noyau de fer. Les effets de l'hystérésis et des courants de Foucault concourent à déformer et à compliquer davantage la forme d'onde du courant, la rendant encore moins sinusoïdale et modifiant sa phase pour qu'elle soit légèrement inférieure à 90° par rapport à la forme d'onde de tension appliquée.
Ce courant de bobine résultant de la somme de tous les effets magnétiques dans le noyau (magnétisation dΦ/dt plus pertes par hystérésis, pertes par courants de Foucault, etc.) est appelé le courant d'excitation .
La distorsion du courant d'excitation d'une inductance à noyau de fer peut être minimisée si elle est conçue et exploitée à de très faibles densités de flux. D'une manière générale, cela nécessite un noyau avec une grande section transversale, ce qui tend à rendre l'inducteur encombrant et coûteux.
Par souci de simplicité, cependant, nous supposerons que notre exemple de noyau est loin de la saturation et exempt de toutes pertes, résultant en un courant d'excitation parfaitement sinusoïdal.
Comme nous l'avons déjà vu dans le chapitre sur les inductances, le fait d'avoir une forme d'onde de courant déphasée de 90° par rapport à la forme d'onde de tension crée une condition dans laquelle la puissance est alternativement absorbée et renvoyée au circuit par l'inductance.
Si l'inducteur est parfait (pas de résistance de fil, pas de pertes de noyau magnétique, etc.), il dissipera une puissance nulle.
Considérons maintenant le même dispositif inducteur, sauf cette fois avec une deuxième bobine (figure ci-dessous) enroulée autour du même noyau de fer. La première bobine sera étiquetée primaire bobine, tandis que la seconde sera étiquetée secondaire :
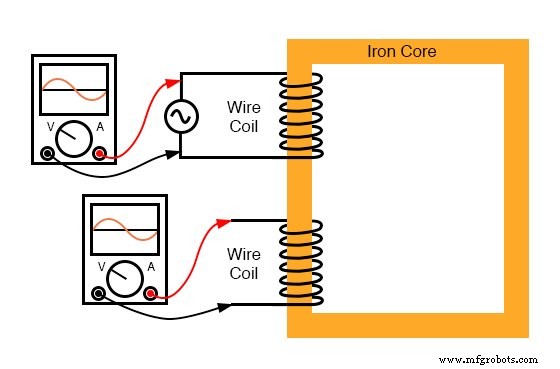
Noyau ferromagnétique avec bobine primaire (à courant alternatif) et bobine secondaire.
Induction mutuelle
Si cette bobine secondaire subit le même changement de flux magnétique que le primaire (ce qui devrait être le cas, en supposant un confinement parfait du flux magnétique à travers le noyau commun), et a le même nombre de tours autour du noyau, une tension d'amplitude et de phase égales à la tension appliquée sera induite sur toute sa longueur.
Dans le graphique suivant, (Figure ci-dessous) la forme d'onde de tension induite est dessinée légèrement plus petite que la forme d'onde de tension source simplement pour distinguer l'une de l'autre :

Le secondaire en circuit ouvert voit le même flux que le primaire. Donc tension secondaire induite es est la même amplitude et la même phase que la tension primaire ep .
Cet effet est appelé inductance mutuelle :l'induction d'une tension dans une bobine en réponse à un changement de courant dans l'autre bobine. Comme l'(auto-)inductance normale, elle est mesurée dans l'unité de henry, mais contrairement à l'inductance normale, elle est symbolisée par la lettre majuscule « M » plutôt que la lettre « L » :

Aucun courant n'existera dans la bobine secondaire car elle est en circuit ouvert. Cependant, si nous y connectons une résistance de charge, un courant alternatif traversera la bobine, en phase avec la tension induite (car la tension aux bornes d'une résistance et le courant qui la traverse sont toujours en phase les uns avec les autres). (Figure ci-dessous)
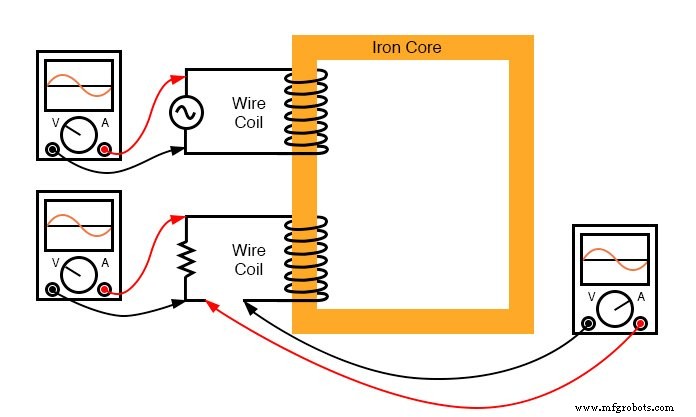
La charge résistive sur le secondaire a une tension et un courant en phase.
Au début, on pourrait s'attendre à ce que ce courant de bobine secondaire provoque un flux magnétique supplémentaire dans le noyau. En fait, ce n'est pas le cas. Si plus de flux était induit dans le noyau, cela entraînerait plus de tension induite dans la bobine primaire (rappelez-vous que e =dΦ/dt).
Cela ne peut pas arriver, car la tension induite de la bobine primaire doit rester à la même amplitude et à la même phase afin de s'équilibrer avec la tension appliquée, conformément à la loi de tension de Kirchhoff. Par conséquent, le flux magnétique dans le noyau ne peut pas être affecté par le courant de la bobine secondaire.
Cependant, qu'est-ce que fait le changement est la quantité de mmf dans le circuit magnétique.
Force magnétomotrice
La force magnétomotrice est produite à chaque fois que le courant traverse un fil. Habituellement, ce mmf est accompagné d'un flux magnétique, conformément à l'équation mmf=ΦR de la « loi d'Ohm magnétique ».
Dans ce cas, cependant, un flux supplémentaire n'est pas autorisé, donc la seule façon dont le mmf de la bobine secondaire peut exister est si un mmf de neutralisation est généré par la bobine primaire, de magnitude égale et de phase opposée.
En effet, c'est ce qui se passe, un courant alternatif se formant dans la bobine primaire, déphasé de 180° par rapport au courant de la bobine secondaire, pour générer ce mmf antagoniste et empêcher un flux de noyau supplémentaire.
Des marques de polarité et des flèches de direction du courant ont été ajoutées à l'illustration pour clarifier les relations de phase :(Figure ci-dessous)
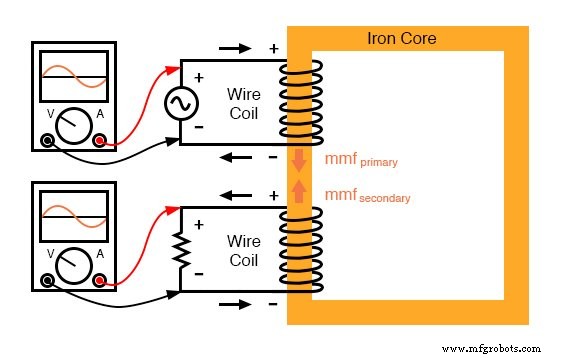
Le flux reste constant avec l'application d'une charge. Cependant, un mmf de neutralisation est produit par le secondaire chargé.
Si vous trouvez ce processus un peu déroutant, ne vous inquiétez pas. La dynamique des transformateurs est un sujet complexe. Ce qu'il est important de comprendre, c'est ceci :lorsqu'une tension alternative est appliquée à la bobine primaire, elle crée un flux magnétique dans le noyau, qui induit une tension alternative dans la bobine secondaire en phase avec la tension source.
Tout courant tiré à travers la bobine secondaire pour alimenter une charge induit un courant correspondant dans la bobine primaire, tirant le courant de la source.
Inductance mutuelle et transformateurs
Remarquez comment la bobine primaire se comporte comme une charge par rapport à la source de tension alternative et comment la bobine secondaire se comporte comme une source par rapport à la résistance.
Plutôt que d'être simplement absorbée et renvoyée alternativement par le circuit de la bobine primaire, l'énergie est maintenant couplée à la bobine secondaire où il est délivré à une charge dissipative (consommante d'énergie). Pour autant que la source « sache », elle alimente directement la résistance.
Bien sûr, il existe également un courant de bobine primaire supplémentaire en retard de 90° sur la tension appliquée, juste assez pour magnétiser le noyau pour créer la tension nécessaire à l'équilibrage par rapport à la source (le courant d'excitation ).
Nous appelons ce type d'appareil un transformateur , car il transforme l'énergie électrique en énergie magnétique, puis de nouveau en énergie électrique. Étant donné que son fonctionnement dépend de l'induction électromagnétique entre deux bobines fixes et d'un flux magnétique d'amplitude et de « polarité » variables, les transformateurs sont nécessairement des appareils à courant alternatif.
Son symbole schématique ressemble à deux inducteurs (bobines) partageant le même noyau magnétique :(Figure ci-dessous)
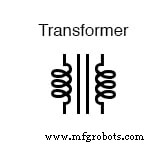
Le symbole schématique d'un transformateur se compose de deux symboles d'inducteur, séparés par des lignes indiquant un noyau ferromagnétique.
Les deux bobines d'inductance se distinguent facilement dans le symbole ci-dessus. La paire de lignes verticales représente un noyau de fer commun aux deux inducteurs. Alors que de nombreux transformateurs ont des matériaux de noyau ferromagnétique, il y en a qui n'en ont pas, leurs inducteurs constitutifs étant liés magnétiquement entre eux par l'air.
La photographie suivante montre un transformateur de puissance du type utilisé dans l'éclairage à décharge de gaz. Ici, les deux bobines d'inductance sont clairement visibles, enroulées autour d'un noyau de fer. Alors que la plupart des conceptions de transformateurs enferment les bobines et le noyau dans un cadre métallique pour la protection, ce transformateur particulier est ouvert pour la visualisation et remplit donc bien son objectif d'illustration (Figure ci-dessous) :

Exemple de transformateur d'éclairage à décharge de gaz.
Enroulements primaire et secondaire
Les deux bobines de fil peuvent être vues ici avec une isolation en vernis de couleur cuivre. La bobine supérieure est plus grande que la bobine inférieure, ayant un plus grand nombre de « tours » autour du noyau. Dans les transformateurs, les bobines d'inductance sont souvent appelées enroulements , en référence au processus de fabrication où le fil est enroulé autour du matériau de base.
Comme modélisé dans notre exemple initial, l'inducteur alimenté d'un transformateur est appelé le primaire enroulement, tandis que la bobine non alimentée est appelée secondaire enroulement.
Sur la photo suivante (figure ci-dessous), un transformateur est représenté coupé en deux, exposant la section transversale du noyau de fer ainsi que les deux enroulements. Comme le transformateur illustré précédemment, cette unité utilise également des enroulements primaires et secondaires de nombres de tours différents.
Le calibre du fil peut également être vu différer entre les enroulements primaires et secondaires. La raison de cette disparité dans le calibre des fils sera expliquée clairement dans la section suivante de ce chapitre.
De plus, le noyau de fer peut être vu sur cette photographie comme étant composé de nombreuses feuilles minces (stratifications) plutôt que d'une pièce solide. La raison en sera également expliquée dans une section ultérieure de ce chapitre.

La coupe transversale du transformateur montre le noyau et les enroulements.
Action de transformation simple à l'aide de SPICE
Il est facile de démontrer l'action d'un transformateur simple à l'aide de SPICE, en configurant les enroulements primaire et secondaire du transformateur simulé comme une paire d'inductances « mutuelles » (figure ci-dessous).
Le coefficient de couplage de champ magnétique est donné à la fin de la ligne "k" dans la description du circuit SPICE, cet exemple étant réglé presque à la perfection (1.000). Ce coefficient décrit à quel point les deux inducteurs sont étroitement «liés» magnétiquement. Plus ces deux inducteurs sont couplés magnétiquement, plus le transfert d'énergie entre eux doit être efficace.
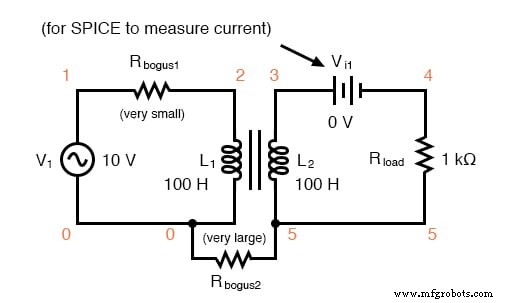
Circuit d'épices pour inducteurs couplés.
Remarque :le Rfaux des résistances sont nécessaires pour satisfaire certaines bizarreries de SPICE. Le premier rompt la boucle par ailleurs continue entre la source de tension et L1 ce qui ne serait pas autorisé par SPICE. Le second fournit un chemin vers la terre (nœud 0) depuis le circuit secondaire, nécessaire car SPICE ne peut pas fonctionner avec des circuits non mis à la terre.
Notez qu'avec des inductances égales pour les deux enroulements (100 henries chacun), les tensions et courants alternatifs sont presque égaux pour les deux. La différence entre les courants primaire et secondaire est le courant magnétisant dont nous avons parlé plus haut :le courant de retard de 90° nécessaire pour magnétiser le noyau.
Comme on le voit ici, il est généralement très faible par rapport au courant primaire induit par la charge, et donc les courants primaire et secondaire sont presque égaux. Ce que vous voyez ici est assez typique de l'efficacité d'un transformateur.
Tout rendement inférieur à 95 % est considéré comme médiocre pour les conceptions de transformateurs de puissance modernes, et ce transfert de puissance se produit sans pièces mobiles ni autres composants sujets à l'usure.
Si nous diminuons la résistance de charge de manière à tirer plus de courant avec la même quantité de tension, nous voyons que le courant à travers l'enroulement primaire augmente en réponse.
Même si la source d'alimentation CA n'est pas directement connectée à la résistance de charge (au contraire, elle est électromagnétiquement « couplée »), la quantité de courant tirée de la source sera presque la même que la quantité de courant qui serait tirée si la charge était directement connecté à la source.
Examinez de près les deux prochaines simulations SPICE, montrant ce qui se passe avec différentes valeurs de résistances de charge :
Remarquez comment le courant primaire suit de près le courant secondaire. Dans notre première simulation, les deux courants étaient d'environ 10 mA, mais maintenant ils sont tous deux d'environ 47 mA. Dans cette seconde simulation, les deux courants sont plus proches de l'égalité, car le courant magnétisant reste le même qu'avant alors que le courant de charge a augmenté.
Notez également comment la tension secondaire a diminué avec la charge plus lourde (courant plus important). Essayons une autre simulation avec une valeur encore plus faible de résistance de charge (15 ) :
Notre courant de charge est maintenant de 0,13 ampères, ou 130 mA, ce qui est nettement plus élevé que la dernière fois. Le courant primaire est très proche d'être le même, mais remarquez comment la tension secondaire est tombée bien en dessous de la tension primaire (1,95 volts contre 10 volts au primaire).
La raison en est une imperfection dans la conception de notre transformateur :parce que les inductances primaire et secondaire ne sont pas parfaitement lié (un facteur k de 0.999 au lieu de 1.000) il y a « égaré » ou « fuite ” inductance. En d'autres termes, une partie du champ magnétique n'est pas liée à la bobine secondaire et ne peut donc pas lui coupler d'énergie :(Figure ci-dessous)
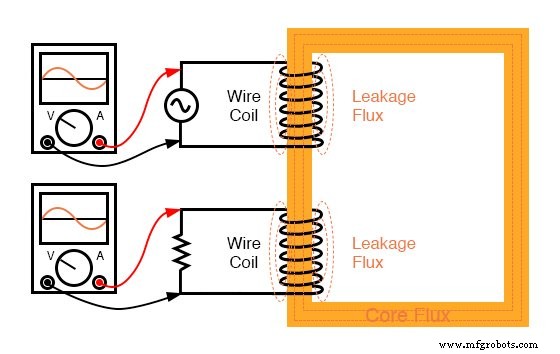
L'inductance de fuite est due au flux magnétique ne coupant pas les deux enroulements.
Par conséquent, ce flux de « fuite » stocke et renvoie simplement de l'énergie au circuit source via une auto-inductance, agissant effectivement comme une impédance série dans les circuits primaire et secondaire. La tension chute à travers cette impédance série, ce qui entraîne une tension de charge réduite :la tension aux bornes de la charge « fléchit » à mesure que le courant de charge augmente. (Figure ci-dessous)
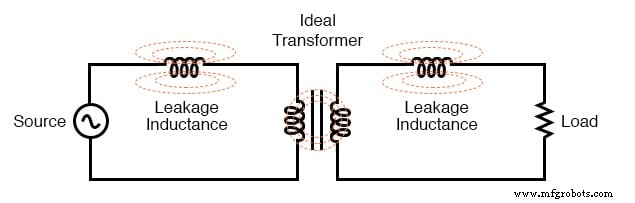
Le circuit équivalent modélise l'inductance de fuite sous forme d'inductances en série indépendantes du « transformateur idéal ».
Si nous modifions la conception du transformateur pour avoir un meilleur couplage magnétique entre les bobines primaire et secondaire, les chiffres de tension entre les enroulements primaire et secondaire seront à nouveau beaucoup plus proches de l'égalité :
Ici, nous voyons que notre tension secondaire est redevenue égale à celle du primaire et que le courant secondaire est également égal au courant primaire. Malheureusement, construire un vrai transformateur avec un couplage aussi complet est très difficile.
Une solution de compromis consiste à concevoir à la fois des bobines primaires et secondaires avec moins d'inductance, la stratégie étant que moins d'inductance dans l'ensemble entraîne moins d'inductance de « fuite » pour causer des problèmes, pour un degré donné d'inefficacité de couplage magnétique. Cela se traduit par une tension de charge plus proche de l'idéal avec la même charge (intensité élevée élevée) et le même facteur de couplage :
En utilisant simplement des bobines primaires et secondaires de moindre inductance, la tension de charge pour cette charge lourde (courant élevé) a été ramenée à des niveaux presque idéaux (9,977 volts). À ce stade, on peut se demander : « Si moins d'inductance est tout ce qui est nécessaire pour obtenir des performances presque idéales sous une charge élevée, alors pourquoi s'inquiéter de l'efficacité du couplage ?
S'il est impossible de construire un transformateur avec un couplage parfait, mais facile de concevoir des bobines à faible inductance, alors pourquoi ne pas simplement construire tous les transformateurs avec des bobines à faible inductance et avoir un excellent rendement même avec un faible couplage magnétique ?"
La réponse à cette question se trouve dans une autre simulation :le même transformateur basse inductance, mais cette fois avec une charge plus légère (moins de courant) de 1 kΩ au lieu de 15 Ω :
Avec des inductances d'enroulement inférieures, les tensions primaire et secondaire sont plus proches d'être égales, mais les courants primaire et secondaire ne le sont pas. Dans ce cas particulier, le courant primaire est de 28,35 mA alors que le courant secondaire n'est que de 9,990 mA :presque trois fois plus de courant dans le primaire que dans le secondaire.
Pourquoi est-ce? Avec moins d'inductance dans l'enroulement primaire, il y a moins de réactance inductive, et par conséquent un courant magnétisant beaucoup plus important. Une quantité substantielle de courant à travers l'enroulement primaire fonctionne simplement pour magnétiser le noyau plutôt que pour transférer énergie utile à l'enroulement secondaire et à la charge.
Un transformateur idéal avec des enroulements primaire et secondaire identiques manifesterait une tension et un courant égaux dans les deux ensembles d'enroulements pour n'importe quelle condition de charge. Dans un monde parfait, les transformateurs transféreraient l'énergie électrique du primaire au secondaire aussi facilement que si la charge était directement connectée à la source d'alimentation primaire, sans aucun transformateur.
Cependant, vous pouvez voir que cet objectif idéal ne peut être atteint que s'il existe un parfait couplage de flux magnétique entre les enroulements primaire et secondaire. Étant donné que cela est impossible à réaliser, les transformateurs doivent être conçus pour fonctionner dans certaines plages de tensions et de charges attendues afin de fonctionner aussi près que possible de l'idéal.
Pour l'instant, la chose la plus importante à garder à l'esprit est le principe de fonctionnement de base d'un transformateur :le transfert de puissance du circuit primaire au circuit secondaire via un couplage électromagnétique.
AVIS :
- Inductance mutuelle est l'endroit où le flux magnétique de deux ou plusieurs inducteurs est « lié » de sorte que la tension est induite dans une bobine proportionnellement au taux de variation du courant dans une autre.
- Un transformateur est un dispositif composé de deux ou plusieurs inductances, dont l'une est alimentée en courant alternatif, induisant une tension alternative aux bornes de la seconde inductance. Si le deuxième inducteur est connecté à une charge, la puissance sera couplée électromagnétiquement de la source d'alimentation du premier inducteur à cette charge.
- L'inductance alimentée dans un transformateur est appelée enroulement primaire . L'inducteur non alimenté dans un transformateur est appelé enroulement secondaire .
- Le flux magnétique dans le noyau (Φ) est en retard de 90° par rapport à la forme d'onde de la tension source. Le courant tiré par la bobine primaire de la source pour produire ce flux est appelé courant magnétisant , et il retarde également la tension d'alimentation de 90°.
- Le courant primaire total dans un transformateur non chargé est appelé courant d'excitation et est composé du courant magnétisant plus tout courant supplémentaire nécessaire pour surmonter les pertes du noyau. Elle n'est jamais parfaitement sinusoïdale dans un vrai transformateur, mais peut l'être davantage si le transformateur est conçu et exploité de manière à ce que la densité de flux magnétique soit réduite au minimum.
- Le flux de noyau induit une tension dans n'importe quelle bobine enroulée autour du noyau. La ou les tensions induites sont idéalement en phase avec la tension de la source d'enroulement primaire et partagent la même forme d'onde.
- Tout courant tiré à travers l'enroulement secondaire par une charge sera « réfléchi » vers l'enroulement primaire et tiré de la source de tension comme si la source alimentait directement une charge similaire.
FICHES DE TRAVAIL CONNEXES :
- Fiche de travail sur l'inductance mutuelle
- Fiche de travail sur les transformateurs d'augmentation, de diminution et d'isolement
Technologie industrielle



