Signaux à ondes carrées
Il a été constaté que tout Une forme d'onde non sinusoïdale répétitive peut être assimilée à une combinaison de tension continue, d'ondes sinusoïdales et/ou d'ondes cosinusoïdales (ondes sinusoïdales avec un déphasage de 90 degrés) à diverses amplitudes et fréquences.
Cela est vrai, peu importe à quel point la forme d'onde en question peut être étrange ou alambiquée. Tant qu'elle se répète régulièrement dans le temps, elle est réductible à cette série d'ondes sinusoïdales.
En particulier, il a été constaté que les ondes carrées sont mathématiquement équivalentes à la somme d'une onde sinusoïdale à cette même fréquence, plus une série infinie d'ondes sinusoïdales impaires-multiples à amplitude décroissante :

Cette vérité sur les formes d'onde peut sembler trop étrange à première vue pour la croire. Cependant, si une onde carrée est en fait une série infinie d'harmoniques d'onde sinusoïdale additionnées, il va de soi que nous devrions pouvoir le prouver en additionnant plusieurs harmoniques d'onde sinusoïdale pour produire une approximation proche d'une onde carrée.
Ce raisonnement est non seulement solide, mais facilement démontré avec SPICE.
Le circuit que nous allons simuler n'est rien de plus que plusieurs sources de tension alternative à onde sinusoïdale d'amplitudes et de fréquences appropriées connectées ensemble en série. Nous utiliserons SPICE pour tracer les formes d'onde de tension à travers des ajouts successifs de sources de tension, comme ceci :
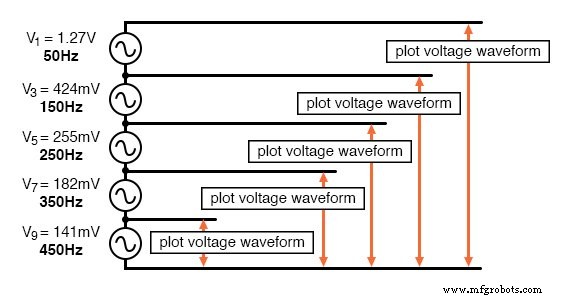
Une onde carrée est approximée par la somme des harmoniques.
Dans cette simulation SPICE particulière, j'ai additionné les 1ère, 3ème, 5ème, 7ème et 9ème sources de tension harmoniques en série pour un total de cinq sources de tension alternative. La fréquence fondamentale est de 50 Hz et chaque harmonique est, bien entendu, un multiple entier de cette fréquence.
Les chiffres d'amplitude (tension) ne sont pas des nombres aléatoires; elles ont plutôt été obtenues grâce aux équations indiquées dans la série de fréquences (la fraction 4/π multipliée par 1, 1/3, 1/5, 1/7, etc. pour chacune des harmoniques impaires croissantes).
Je vais raconter l'analyse étape par étape à partir d'ici, en expliquant ce que nous examinons. Dans ce premier tracé, nous voyons l'onde sinusoïdale de fréquence fondamentale de 50 Hz par elle-même. Ce n'est rien d'autre qu'une forme sinusoïdale pure, sans contenu harmonique supplémentaire. Voici le type de forme d'onde produite par une source d'alimentation secteur idéale :
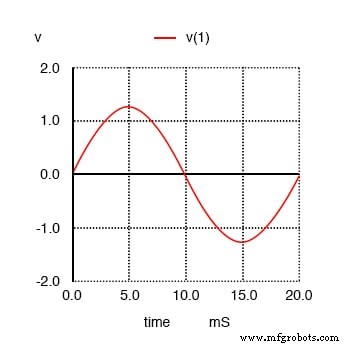
Onde sinusoïdale pure 50 Hz.
Ensuite, nous voyons ce qui se passe lorsque cette forme d'onde claire et simple est combinée avec la troisième harmonique (trois fois 50 Hz, ou 150 Hz). Soudain, cela ne ressemble plus à une onde sinusoïdale nette :
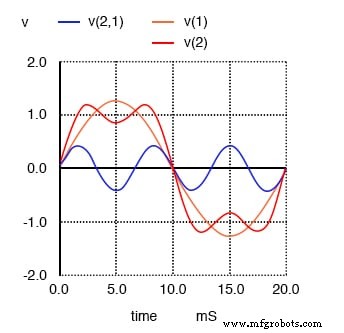
La somme des 1er (50 Hz) et 3e (150 Hz) harmoniques correspond approximativement à une onde carrée de 50 Hz.
Les temps de montée et de descente entre les cycles positifs et négatifs sont maintenant beaucoup plus raides, et les crêtes de la vague sont plus proches de devenir plates comme une onde carrée. Regardez ce qui se passe lorsque nous ajoutons la prochaine fréquence harmonique impaire :
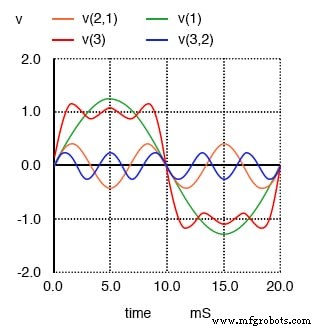
La somme des 1er, 3e et 5e harmoniques se rapproche de l'onde carrée.
Le changement le plus notable ici est la façon dont les crêtes de la vague se sont encore plus aplaties. Il y a plusieurs creux et crêtes à chaque extrémité de la vague, mais ces creux et crêtes sont d'amplitude plus petite qu'auparavant. Regardez à nouveau pendant que nous ajoutons la prochaine forme d'onde harmonique impaire au mix :
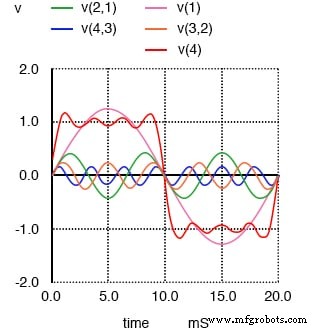
La somme des 1er, 3e, 5e et 7e harmoniques se rapproche de l'onde carrée.
Ici, nous pouvons voir la vague devenir plus plate à chaque pic. Enfin, en ajoutant la 9e harmonique, la cinquième source de tension sinusoïdale de notre circuit, nous obtenons ce résultat :
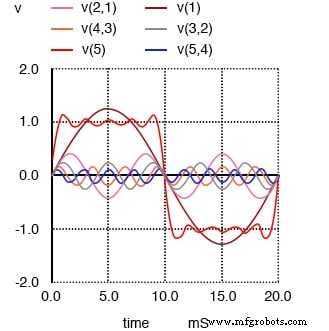
La somme des 1er, 3e, 5e, 7e et 9e harmoniques se rapproche de l'onde carrée.
Le résultat final de l'addition des cinq premières formes d'onde harmoniques impaires (toutes aux amplitudes appropriées, bien sûr) est une approximation proche d'une onde carrée. Le but en faisant cela est d'illustrer comment nous pouvons construire une onde carrée à partir de plusieurs ondes sinusoïdales à différentes fréquences, pour prouver qu'une onde carrée pure est en fait équivalente à une série d'ondes sinusoïdales.
Lorsqu'une tension alternative carrée est appliquée à un circuit avec des composants réactifs (condensateurs et inductances), ces composants réagissent comme s'ils étaient exposés à plusieurs tensions sinusoïdales de fréquences différentes, ce qu'elles sont en fait.
Le fait que des ondes non sinusoïdales répétitives soient équivalentes à une série définie de tensions continues additives, d'ondes sinusoïdales et/ou d'ondes cosinusoïdales est une conséquence du fonctionnement des ondes :une propriété fondamentale de tous les phénomènes liés aux ondes, électriques ou autres.
Le processus mathématique de réduction d'une onde non sinusoïdale en ces fréquences constitutives est appelé analyse de Fourier , dont les détails dépassent largement le cadre de ce texte. Cependant, des algorithmes informatiques ont été créés pour effectuer cette analyse à grande vitesse sur des formes d'onde réelles, et son application à la qualité du courant alternatif et à l'analyse du signal est très répandue.
SPICE a la capacité d'échantillonner une forme d'onde et de la réduire en ses harmoniques d'onde sinusoïdale constitutives au moyen d'une transformée de Fourier algorithme, produisant l'analyse de fréquence sous la forme d'un tableau de nombres. Essayons ceci sur une onde carrée, dont nous savons déjà qu'elle est composée d'ondes sinusoïdales impaires :
netlist d'analyse des ondes carrées v1 1 0 impulsion (-1 1 0 .1m .1m 10m 20m) r1 1 0 10k .tran 1m 40m .plot tran v(1,0) .quatre 50 v(1,0) .finir
Le pulse option dans la ligne netlist décrivant la source de tension v1 indique à SPICE de simuler une forme d'onde "d'impulsion" de forme carrée, dans ce cas symétrique (temps égal pour chaque demi-cycle) et a une amplitude de crête de 1 volt. Tout d'abord, nous allons tracer l'onde carrée à analyser :
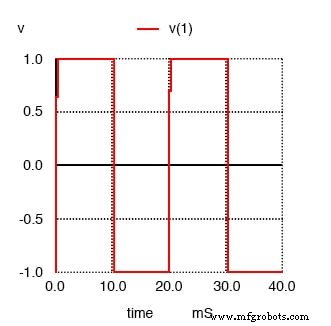
Squarewave pour l'analyse de Fourier SPICE
Ensuite, nous imprimerons l'analyse de Fourier générée par SPICE pour cette onde carrée :
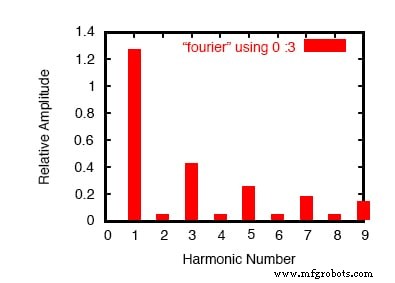
Tracé des résultats de l'analyse de Fourier.
Ici, (Figure ci-dessus) SPICE a décomposé la forme d'onde en un spectre de fréquences sinusoïdales jusqu'à la neuvième harmonique, plus une petite tension continue étiquetée Composant continu .
J'ai dû informer SPICE de la fréquence fondamentale (pour un signal carré avec une période de 20 millisecondes, cette fréquence est de 50 Hz), il a donc su classer les harmoniques. Notez à quel point les chiffres sont petits pour toutes les harmoniques paires (2e, 4e, 6e, 8e) et comment les amplitudes des harmoniques impaires diminuent (1er est le plus grand, 9e est le plus petit).
Cette même technique de "Transformation de Fourier" est souvent utilisée dans l'instrumentation de puissance informatisée, échantillonnant la ou les formes d'onde CA et déterminant leur contenu harmonique. Un algorithme informatique commun (séquence d'étapes de programme pour effectuer une tâche) pour cela est la Fast Fourier Transform ou FFT fonction.
Vous n'avez pas besoin de vous préoccuper du fonctionnement exact de ces routines informatiques, mais soyez conscient de leur existence et de leur application.
Cette même technique mathématique utilisée dans SPICE pour analyser le contenu harmonique des ondes peut être appliquée à l'analyse technique de la musique :décomposer un son particulier en ses fréquences sinusoïdales constitutives.
En fait, vous avez peut-être déjà vu un appareil conçu pour cela sans vous rendre compte de ce que c'était ! Un égaliseur graphique est une pièce d'équipement stéréo haute fidélité qui contrôle (et parfois affiche) la nature du contenu harmonique de la musique.
Équipé de plusieurs boutons ou leviers coulissants, l'égaliseur est capable d'atténuer (réduire) sélectivement l'amplitude de certaines fréquences présentes dans la musique, pour « personnaliser » le son au profit de l'auditeur. En règle générale, il y aura un affichage "graphique à barres" à côté de chaque levier de commande, affichant l'amplitude de chaque fréquence particulière.
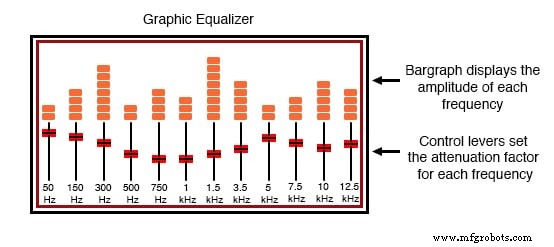
Égaliseur graphique audio Hi-Fi.
Un appareil conçu strictement pour afficher (et non contrôler) les amplitudes de chaque plage de fréquences pour un signal à fréquences mixtes est généralement appelé un analyseur de spectre .
La conception des analyseurs de spectre peut être aussi simple qu'un ensemble de circuits de « filtre » (voir le chapitre suivant pour plus de détails) conçu pour séparer les différentes fréquences les unes des autres, ou aussi complexe qu'un ordinateur numérique spécialisé exécutant un algorithme FFT pour diviser mathématiquement le signal en ses composantes harmoniques.
Les analyseurs de spectre sont souvent conçus pour analyser des signaux à très haute fréquence, tels que ceux produits par les émetteurs radio et le matériel de réseau informatique. Sous cette forme, ils ont souvent l'apparence d'un oscilloscope :
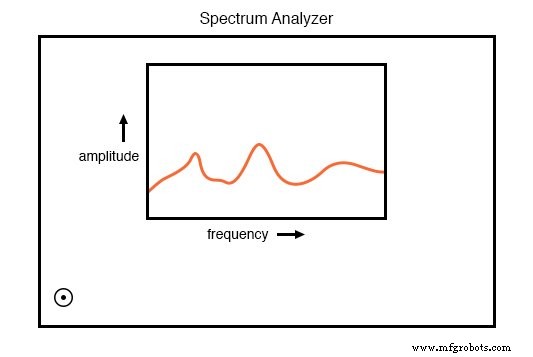
L'analyseur de spectre montre l'amplitude en fonction de la fréquence.
Comme un oscilloscope, l'analyseur de spectre utilise un tube cathodique (ou un écran d'ordinateur imitant un tube cathodique) pour afficher un tracé du signal.
Contrairement à un oscilloscope, ce tracé est l'amplitude sur la fréquence plutôt qu'une amplitude dans le temps . Essentiellement, un analyseur de fréquence donne à l'opérateur un tracé de Bode du signal :quelque chose qu'un ingénieur pourrait appeler un domaine fréquentiel plutôt qu'un domaine temporel analyse.
Le terme « domaine » est mathématique :un mot sophistiqué pour décrire l'axe horizontal d'un graphique. Ainsi, le tracé de l'amplitude (verticale) d'un oscilloscope au fil du temps (horizontal) est une analyse du « domaine temporel », tandis que le tracé de l'amplitude (verticale) d'un analyseur de spectre sur la fréquence (horizontale) est une analyse du « domaine fréquentiel ».
Lorsque nous utilisons SPICE pour tracer l'amplitude du signal (amplitude de tension ou de courant) sur une plage de fréquences, nous effectuons un domaine fréquentiel analyse.
Veuillez noter que l'analyse de Fourier de la dernière simulation SPICE n'est pas "parfaite". Idéalement, les amplitudes de toutes les harmoniques paires doivent être absolument nulles, de même que la composante continue. Encore une fois, ce n'est pas tant une bizarrerie de SPICE qu'une propriété des formes d'onde en général.
Une forme d'onde de durée infinie (nombre infini de cycles) peut être analysée avec une précision absolue, mais moins l'ordinateur dispose de cycles pour l'analyse, moins l'analyse est précise. Ce n'est que lorsque nous avons une équation décrivant une forme d'onde dans son intégralité que l'analyse de Fourier peut la réduire à une série définie de formes d'onde sinusoïdales.
Moins une onde a de cycles, moins sa fréquence est certaine. En poussant ce concept à son extrême logique, une impulsion courte - une forme d'onde qui ne termine même pas un cycle - en fait n'a pas de fréquence , mais agit plutôt comme une gamme infinie de fréquences. Ce principe est commun à tous phénomènes basés sur les ondes, pas seulement les tensions et courants alternatifs.
Il suffit de dire que le nombre de cycles et la certitude des composants de fréquence d'une forme d'onde sont directement liés.
Nous pourrions améliorer la précision de notre analyse ici en laissant l'onde osciller encore et encore pendant de nombreux cycles, et le résultat serait une analyse de spectre plus conforme à l'idéal. Dans l'analyse suivante, j'ai omis le tracé de la forme d'onde par souci de concision, c'est juste une très longue onde carrée :
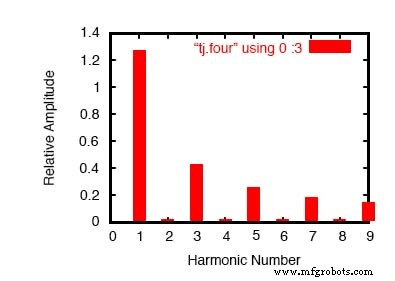
Analyse de Fourier améliorée.
Remarquez comment cette analyse (figure ci-dessus) montre moins de tension de composante continue et des amplitudes plus faibles pour chacune des ondes sinusoïdales à fréquence harmonique paire, tout cela parce que nous laissons l'ordinateur échantillonner plus de cycles de l'onde. Encore une fois, l'imprécision de la première analyse n'est pas tant un défaut de SPICE qu'une propriété fondamentale des ondes et de l'analyse du signal.
AVIS :
- Les ondes carrées sont équivalentes à une onde sinusoïdale à la même fréquence (fondamentale) ajoutée à une série infinie d'harmoniques sinusoïdales impaires-multiples à des amplitudes décroissantes.
- Il existe des algorithmes informatiques capables d'échantillonner des formes d'onde et de déterminer leurs composantes sinusoïdales constitutives. La Transformée de Fourier algorithme (en particulier la Fast Fourier Transform , ou FFT ) est couramment utilisé dans les programmes de simulation de circuits informatiques tels que SPICE et dans les équipements de mesure électroniques pour déterminer la qualité de l'alimentation.
FICHES DE TRAVAIL CONNEXES :
- Fiche de travail sur les signaux d'onde carrée
Technologie industrielle
- Signaux
- Le réseau neuronal artificiel peut améliorer la communication sans fil
- Un nouveau circuit détecte les signaux radio les plus faibles autorisés par la mécanique quantique
- Le nouvel algorithme fusionne en toute transparence deux signaux audio
- Le nouvel ordinateur ADN peut calculer jusqu'à 900 racines carrées
- La prochaine vague de startups directes aux consommateurs arrive
- Lignes directrices pour la conception RF et micro-ondes
- Soudage à la vague vs soudage par refusion
- Guide des problèmes de soudure à la vague pour les PCB



