Facteur Q et bande passante d'un circuit résonant

Le facteur Q, ou qualité, d'un circuit résonant est une mesure de la « bonté » ou de la qualité d'un circuit résonant. Une valeur plus élevée pour cette figure de mérite correspond à une bande passante plus étroite, ce qui est souhaitable dans de nombreuses applications. Plus formellement, Q est le rapport entre la puissance stockée et la puissance dissipée dans la réactance et la résistance du circuit, respectivement :

Q =Pstocké /Pdissipée =I
2
 X/I
2
 R Q =X/R où :X =Réactance capacitive ou inductive à la résonance R =Résistance série. 

Cette formule est applicable aux circuits résonants en série, ainsi qu'aux circuits résonants en parallèle si la résistance est en série avec l'inducteur. C'est le cas dans les applications pratiques, car nous nous intéressons principalement à la résistance de l'inducteur limitant le Q.

Remarque : Certains textes peuvent montrer X et R intervertis dans la formule "Q" pour un circuit résonant parallèle. Ceci est correct pour une grande valeur de R en parallèle avec C et L. Notre formule est correcte pour un petit R en série avec L.

Une application pratique de « Q » est que la tension aux bornes de L ou C dans un circuit résonant en série est Q fois la tension appliquée totale. Dans un circuit résonant parallèle, le courant à travers L ou C est Q fois le courant total appliqué.

Circuits résonants en série

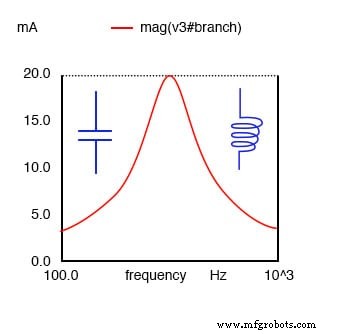
Un circuit résonant en série ressemble à une résistance à la fréquence de résonance. Puisque la définition de la résonance est X_L =X_C , les composants réactifs s'annulent, ne laissant que la résistance pour contribuer à l'impédance.

L'impédance est également au minimum à la résonance. En dessous de la fréquence de résonance, le circuit résonant en série semble capacitif puisque l'impédance du condensateur augmente jusqu'à une valeur supérieure à la réactance inductive décroissante, laissant une valeur capacitive nette.

Au-dessus de la résonance, la réactance inductive augmente, la réactance capacitive diminue, laissant une composante inductive nette.

REMARQUE :

À la résonance, le circuit résonant en série apparaît purement résistif. En dessous de la résonance, il semble capacitif. Au-dessus de la résonance, il apparaît inductif. Le courant est maximum à la résonance, l'impédance au minimum. Le courant est défini par la valeur de la résistance. Au-dessus ou au-dessous de la résonance, l'impédance augmente.

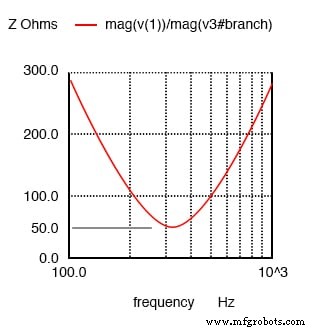
L'impédance est au minimum à la résonance dans un circuit résonant en série.

Le pic de courant de résonance peut être modifié en faisant varier la résistance série, ce qui modifie le Q. Cela affecte également la largeur de la courbe. Un circuit à faible résistance et à Q élevé a une bande passante étroite, par rapport à un circuit à haute résistance et à faible Q.

Bande passante en termes de Q et de fréquence de résonance :

 BW =fc /Q Où fc =fréquence de résonance Q =facteur de qualité

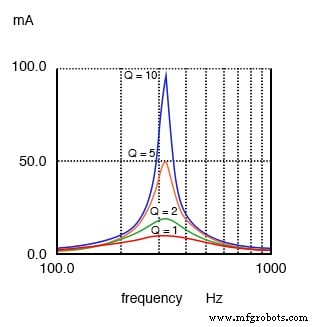
Un circuit résonant à Q élevé a une bande passante étroite par rapport à un Q faible

La bande passante est mesurée entre les points d'amplitude actuels de 0,707. Les 0,707 points de courant correspondent aux demi-points de puissance puisque P =I ² R, (0,707) ² =(0,5).

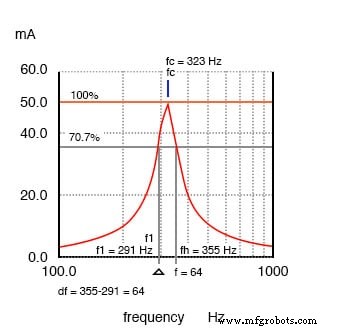
La bande passante, Δf est mesurée entre les points d'amplitude de 70,7% du circuit résonant en série.

 BW =Δf =fh -fl =fc /Q Où :fh =bord de bande haute fl =bord de bande bas fl =fc - Δf/2 fh =fc + Δf/2 Où fc =fréquence centrale (fréquence de résonance)

Dans la figure ci-dessus, le point de courant à 100 % est de 50 mA. Le niveau de 70,7 % est 0,707 (50 mA) =35,4 mA. Les bords de bande supérieur et inférieur lus sur la courbe sont de 291 Hz pour fl et de 355 Hz pour f_h . La bande passante est de 64 Hz et les demi-points de puissance sont de ± 32 Hz de la fréquence de résonance centrale :

 BW =Δf =fh -fl =355-291 =64 fl =fc - f/2 =323-32 =291 fh =fc + Δf/2 =323+32 =355

Puisque BW =fc/Q :

Q =f_c /BW =(323 Hz)/(64 Hz) =5

Circuits de résonance parallèles

L'impédance d'un circuit résonant parallèle est maximale à la fréquence de résonance. En dessous de la fréquence de résonance, le circuit résonant parallèle semble inductif car l'impédance de l'inducteur est plus faible, attirant la plus grande proportion de courant.

Au-dessus de la résonance, la réactance capacitive diminue, tirant le courant le plus important, prenant ainsi une caractéristique capacitive.

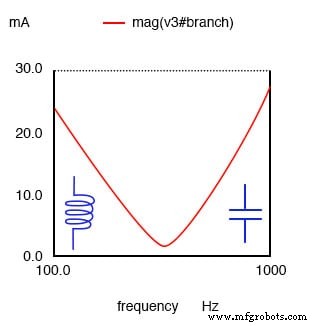
Un circuit résonant parallèle est résistif à la résonance, inductif au-dessous de la résonance, capacitif au-dessus de la résonance.

L'impédance est maximale à la résonance dans un circuit résonant parallèle, mais diminue au-dessus ou au-dessous de la résonance. La tension est à un pic à la résonance puisque la tension est proportionnelle à l'impédance (E=IZ).

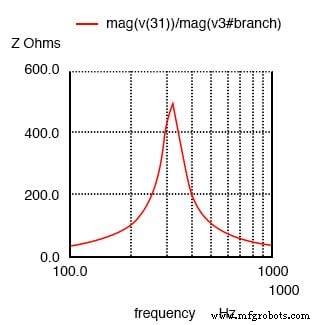
Circuit résonant parallèle :pics d'impédance à la résonance.

Un faible Q dû à une résistance élevée en série avec l'inducteur produit un faible pic sur une large courbe de réponse pour un circuit résonant parallèle. Un Q élevé est dû à une faible résistance en série avec l'inducteur. Cela produit un pic plus élevé dans la courbe de réponse plus étroite. Le Q élevé est obtenu en enroulant l'inducteur avec un plus grand diamètre (plus petit calibre), un fil de résistance inférieure.

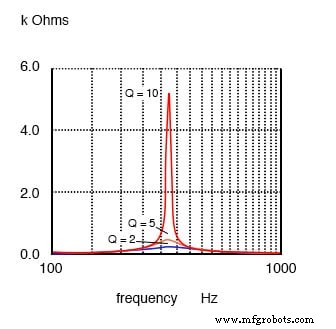
La réponse de résonance parallèle varie avec Q.

La bande passante de la courbe de réponse résonante parallèle est mesurée entre les points à mi-puissance. Cela correspond aux points de tension de 70,7 % puisque la puissance est proportionnelle à E ² . ((0.707) ² =0,50) La tension étant proportionnelle à l'impédance, nous pouvons utiliser la courbe d'impédance.

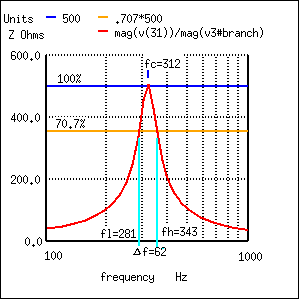
La bande passante, Δf est mesurée entre les points d'impédance de 70,7% d'un circuit résonant parallèle.

Dans la figure ci-dessus, le point d'impédance à 100 % est de 500 Ω. Le niveau de 70,7% est 0707(500)=354 Ω. Les bords de bande supérieur et inférieur lus sur la courbe sont de 281 Hz pour fl et de 343 Hz pour fh. La bande passante est de 62 Hz et les demi-points de puissance sont de ± 31 Hz de la fréquence de résonance centrale :

BW =Δf =fh -fl =343-281 =62 fl =fc - f/2 =312-31 =281 fh =fc + Δf/2 =312+31 =343

Q =fc/BW =(312 Hz)/(62 Hz) =5

FICHES DE TRAVAIL CONNEXES :

• Feuille de travail sur la résonance
• Feuille de travail sur la substitution algébrique des circuits électriques