Circuits série résistance-inductance
Dans la section précédente, nous avons exploré ce qui se passerait dans les circuits alternatifs simples à résistance uniquement et à inductance uniquement. Nous allons maintenant mélanger les deux composants sous forme de série et étudier les effets.
Exemple de circuit d'inductance de résistance en série
Prenez ce circuit comme exemple pour travailler avec :
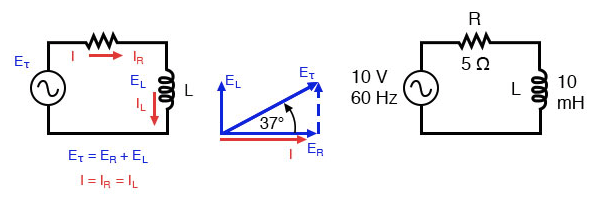
Circuit d'inductance de résistance en série :le courant retarde la tension appliquée de 0o à 90o.
La résistance offrira 5 de résistance au courant alternatif quelle que soit la fréquence, tandis que l'inductance offrira 3,7699 Ω de réactance au courant alternatif à 60 Hz.
Parce que la résistance de la résistance est un nombre réel (5 ∠ 0°, ou 5 + j0 Ω), et la réactance de l'inducteur est un nombre imaginaire (3.7699 Ω ∠ 90°, ou 0 + j3.7699 Ω), l'effet combiné de les deux composantes seront une opposition au courant égale à la somme complexe des deux nombres.
Cette opposition combinée sera une combinaison vectorielle de résistance et de réactance. Afin d'exprimer succinctement cette opposition, nous avons besoin d'un terme plus complet pour l'opposition au courant que la résistance ou la réactance seules.
Ce terme est appelé impédance , son symbole est Z, et il s'exprime également dans l'unité d'ohms, tout comme la résistance et la réactance. Dans l'exemple ci-dessus, l'impédance totale du circuit est :

Résistance dans la loi d'Ohm
L'impédance est liée à la tension et au courant comme vous pouvez vous y attendre, d'une manière similaire à la résistance dans la loi d'Ohm :

En fait, il s'agit d'une forme beaucoup plus complète de la loi d'Ohm que ce qui a été enseigné en électronique à courant continu (E =IR), tout comme l'impédance est une expression beaucoup plus complète de l'opposition au flux de courant que ne l'est la résistance. Tout la résistance et toute réactance, séparément ou en combinaison (série/parallèle), peuvent être et doivent être représentées comme une seule impédance dans un circuit alternatif.
Pour calculer le courant dans le circuit ci-dessus, nous devons d'abord donner une référence d'angle de phase pour la source de tension, qui est généralement supposée être nulle. (Les angles de phase de l'impédance résistive et inductive sont toujours 0° et +90°, respectivement, quels que soient les angles de phase donnés pour la tension ou le courant).
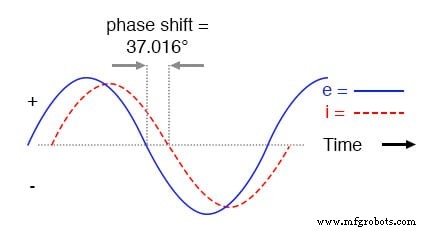
Comme pour le circuit purement inductif, l'onde de courant est en retard sur l'onde de tension (de la source), bien que cette fois le décalage ne soit pas aussi important :seulement 37,016° contre un plein 90° comme c'était le cas dans le circuit purement inductif .

La tension de décalage actuelle dans un circuit L-R en série.
Pour la résistance et l'inductance, les relations de phase entre la tension et le courant n'ont pas changé. La tension aux bornes de la résistance est en phase (décalage de 0°) avec le courant qui la traverse, et la tension aux bornes de l'inductance est déphasée de +90° avec le courant qui la traverse. Nous pouvons vérifier cela mathématiquement :

La tension aux bornes de la résistance a exactement le même angle de phase que le courant qui la traverse, nous indiquant que E et I sont en phase (pour la résistance uniquement).

La tension aux bornes de l'inducteur a un angle de phase de 52,984°, tandis que le courant à travers l'inducteur a un angle de phase de -37,016°, une différence d'exactement 90° entre les deux. Cela nous indique que E et I sont toujours déphasés de 90° (pour l'inducteur uniquement).
Utilisez la loi de tension de Kirchhoff
Nous pouvons également prouver mathématiquement que ces valeurs complexes s'additionnent pour former la tension totale, tout comme la loi de tension de Kirchhoff le prédirait :

Calculer à l'aide de SPICE
Vérifions la validité de nos calculs avec SPICE :
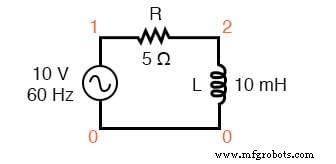
Circuit d'épices :R-L.

Notez que tout comme avec les circuits CC, SPICE produit des valeurs de courant comme s'ils étaient négatifs (180° hors phase) avec la tension d'alimentation. Au lieu d'un angle de phase de -37,016°, nous obtenons un angle de phase actuel de 143°(-37° + 180°).
Ceci est simplement une idiosyncrasie de SPICE et ne représente rien de significatif dans la simulation de circuit elle-même. Notez comment les lectures de phase de tension de résistance et d'inductance correspondent à nos calculs (-37,02° et 52,98°, respectivement), exactement comme nous nous y attendions.
Avec tous ces chiffres à suivre pour un circuit aussi simple que celui-ci, il serait avantageux pour nous d'utiliser la méthode du «tableau». L'application d'un tableau à ce simple circuit résistance-inductance en série se déroulerait comme tel.
Tout d'abord, établissez un tableau pour les chiffres E/I/Z et insérez toutes les valeurs des composants dans ces termes (en d'autres termes, n'insérez pas les valeurs réelles de résistance ou d'inductance en ohms et en henry, respectivement, dans le tableau ; convertissez-les plutôt en figures complexes d'impédance et écrivez-les dans :
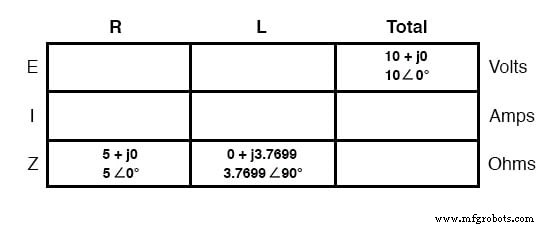
Bien que ce ne soit pas nécessaire, je trouve utile d'écrire les deux les formes rectangulaires et polaires de chaque quantité dans le tableau. Si vous utilisez une calculatrice capable d'effectuer des calculs arithmétiques complexes sans avoir besoin de conversion entre les formes rectangulaires et polaires, cette documentation supplémentaire est totalement inutile.
Cependant, si vous êtes obligé d'effectuer des opérations arithmétiques complexes « à la main » (addition et soustraction sous forme rectangulaire, et multiplication et division sous forme polaire), l'écriture de chaque quantité sous les deux formes sera en effet utile.
Maintenant que nos chiffres « donnés » sont insérés à leurs emplacements respectifs dans le tableau, nous pouvons procéder comme avec DC :déterminer l'impédance totale à partir des impédances individuelles. Puisqu'il s'agit d'un circuit série, on sait que l'opposition au passage du courant (résistance ou impédance) ajoute pour former l'opposition totale :
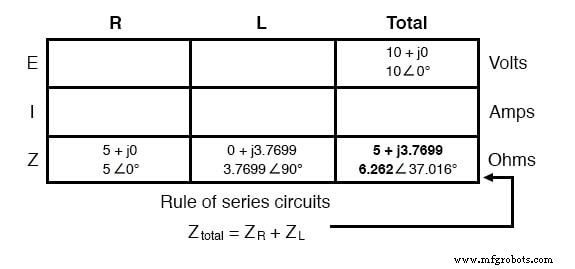
Maintenant que nous connaissons la tension totale et l'impédance totale, nous pouvons appliquer la loi d'Ohm (I=E/Z) pour déterminer le courant total :
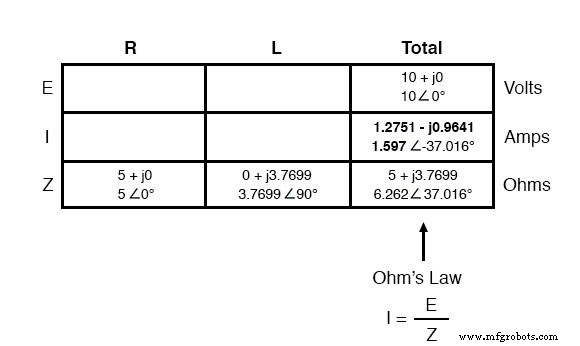
Tout comme pour le courant continu, le courant total dans un circuit alternatif en série est partagé également par tous les composants. Cela est toujours vrai car dans un circuit en série, il n'y a qu'un seul chemin pour que le courant circule, donc le débit de leur flux doit être uniforme partout. Par conséquent, nous pouvons transférer les chiffres du courant dans les colonnes de la résistance et de l'inducteur :
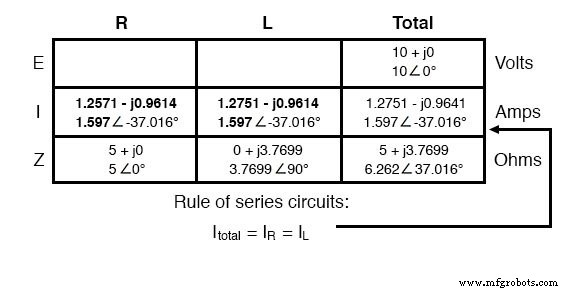
Il ne reste plus qu'à comprendre la chute de tension aux bornes de la résistance et de l'inductance, respectivement. Cela se fait grâce à l'utilisation de la loi d'Ohm (E=IZ), appliquée verticalement dans chaque colonne du tableau :
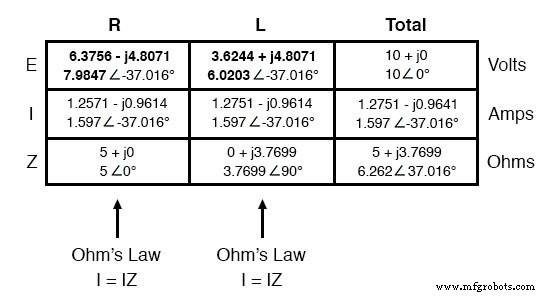
Et avec ça, notre tableau est complet. Les mêmes règles que nous avons appliquées dans l'analyse des circuits CC s'appliquent également aux circuits CA, avec la mise en garde que toutes les quantités doivent être représentées et calculées sous une forme complexe plutôt que scalaire.
Tant que le déphasage est correctement représenté dans nos calculs, il n'y a pas de différence fondamentale dans la façon dont nous abordons l'analyse de base des circuits CA par rapport au CC.
C'est maintenant le bon moment pour revoir la relation entre ces chiffres calculés et les lectures données par les mesures réelles des instruments de tension et de courant.
Les chiffres ici qui se rapportent directement aux mesures réelles sont ceux en notation polaire , pas rectangulaire ! En d'autres termes, si vous deviez connecter un voltmètre aux bornes de la résistance de ce circuit, cela indiquerait 7,9847 volts, pas 6,3756 (rectangulaire réel) ou 4,8071 (rectangulaire imaginaire).
Pour décrire cela en termes graphiques, les instruments de mesure vous indiquent simplement la durée du vecteur pour cette quantité particulière (tension ou courant).
La notation rectangulaire, bien que pratique pour l'addition et la soustraction arithmétiques, est une forme de notation plus abstraite que polaire par rapport aux mesures du monde réel. Comme je l'ai dit précédemment, j'indiquerai à la fois les formes polaires et rectangulaires de chaque quantité dans mes tableaux de circuits CA simplement pour faciliter le calcul mathématique.
Ce n'est pas absolument nécessaire, mais peut être utile pour ceux qui suivent sans l'avantage d'une calculatrice avancée. Si nous devions nous limiter à l'utilisation d'une seule forme de notation, le meilleur choix serait polaire, car c'est la seule qui puisse être directement corrélée à des mesures réelles.
L'impédance (Z) d'un circuit série R-L peut être calculée, compte tenu de la résistance (R) et de la réactance inductive (XL). Puisque E=IR, E=IXL et E=IZ, la résistance, la réactance et l'impédance sont respectivement proportionnelles à la tension. Ainsi, le diagramme de phaseur de tension peut être remplacé par un diagramme d'impédance similaire.
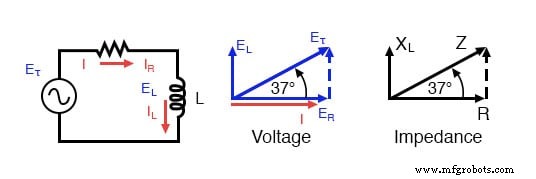
Série :Circuit R-L Diagramme de phaseur d'impédance.
Exemple : Soit :Une résistance de 40 Ω en série avec une inductance de 79,58 millihenry. Trouvez l'impédance à 60 hertz.
AVIS :
- Impédance est la mesure totale de l'opposition au courant électrique et est la somme complexe (vecteur) de la résistance («réelle») et de la réactance («imaginaire»). Il est symbolisé par la lettre « Z » et mesuré en ohms, tout comme la résistance (R) et la réactance (X).
- Les impédances (Z) sont gérées comme les résistances (R) dans l'analyse des circuits en série :les impédances en série s'additionnent pour former l'impédance totale. Assurez-vous simplement d'effectuer tous les calculs sous forme complexe (non scalaire) ! ZTotal =Z1 + Z2 + . . . Zn
- Une impédance purement résistive aura toujours un angle de phase d'exactement 0° (ZR =R ∠ 0°).
- Une impédance purement inductive aura toujours un angle de phase d'exactement +90° (ZL =XL ∠ 90°).
- Loi d'Ohm pour les circuits AC :E =IZ; I =E/Z; Z =E/I
- Lorsque des résistances et des inductances sont mélangées dans des circuits, l'impédance totale aura un angle de phase compris entre 0° et +90°. Le courant du circuit aura un angle de phase compris entre 0° et -90°.
- Les circuits CA en série présentent les mêmes propriétés fondamentales que les circuits CC en série :le courant est uniforme dans tout le circuit, les chutes de tension s'additionnent pour former la tension totale et les impédances s'additionnent pour former l'impédance totale.
FICHES DE TRAVAIL CONNEXES :
- Fiche de travail des inducteurs
- Fiche de travail sur la résistance, la réactance et l'impédance
- Fiche de travail sur la réactance inductive
Technologie industrielle



