Introduction aux nombres complexes

Si j'avais besoin de décrire la distance entre deux villes, je pourrais fournir une réponse consistant en un seul nombre en miles, kilomètres ou une autre unité de mesure linéaire.

Cependant, si je devais décrire comment voyager d'une ville à l'autre, je devrais fournir plus d'informations que la distance entre ces deux villes; Je devrais également fournir des informations sur la direction voyager aussi.

Le type d'information qui exprime une dimension unique, telle que la distance linéaire, est appelé un scalaire quantité en mathématiques. Les nombres scalaires sont le type de nombres que vous avez utilisé jusqu'à présent dans la plupart de vos applications mathématiques.

La tension produite par une batterie, par exemple, est une grandeur scalaire. Il en va de même pour la résistance d'un morceau de fil (ohms) ou le courant qui le traverse (ampères).

Cependant, lorsque nous commençons à analyser les circuits alternatifs, nous trouvons cette quantité de tension, de courant et même de résistance (appelée impédance en courant alternatif) ne sont pas les quantités unidimensionnelles familières que nous avons l'habitude de mesurer dans les circuits à courant continu.

Au contraire, ces grandeurs, parce qu'elles sont dynamiques (alternance de direction et d'amplitude), possèdent d'autres dimensions dont il faut tenir compte. La fréquence et le déphasage sont deux de ces dimensions qui entrent en jeu.

Même avec des circuits AC relativement simples, où nous n'avons affaire qu'à une seule fréquence, nous avons toujours la dimension du déphasage à affronter en plus de l'amplitude.

Afin d'analyser avec succès les circuits AC, nous devons travailler avec des objets et des techniques mathématiques capables de représenter ces quantités multidimensionnelles.

C'est ici que nous devons abandonner les nombres scalaires pour quelque chose de mieux adapté :nombres complexes . Tout comme l'exemple des directions d'une ville à une autre, les grandeurs AC dans un circuit monofréquence ont à la fois une amplitude (analogie :distance) et un déphasage (analogie :direction).

Un nombre complexe est une quantité mathématique unique capable d'exprimer ces deux dimensions d'amplitude et de déphasage à la fois.

Représentation graphique des nombres complexes

Les nombres complexes sont plus faciles à saisir lorsqu'ils sont représentés graphiquement. Si je trace une ligne avec une certaine longueur (grandeur) et angle (direction), j'ai une représentation graphique d'un nombre complexe qui est communément appelé en physique un vecteur :(Figure ci-dessous)

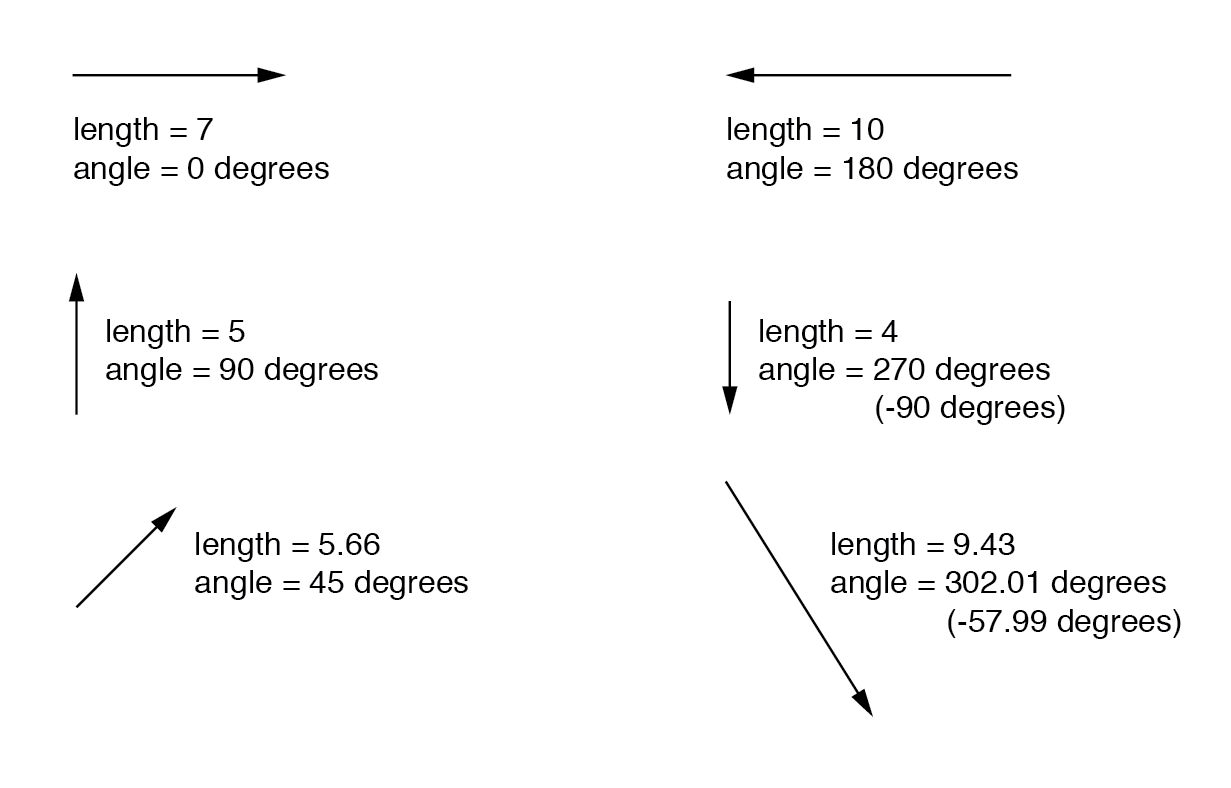
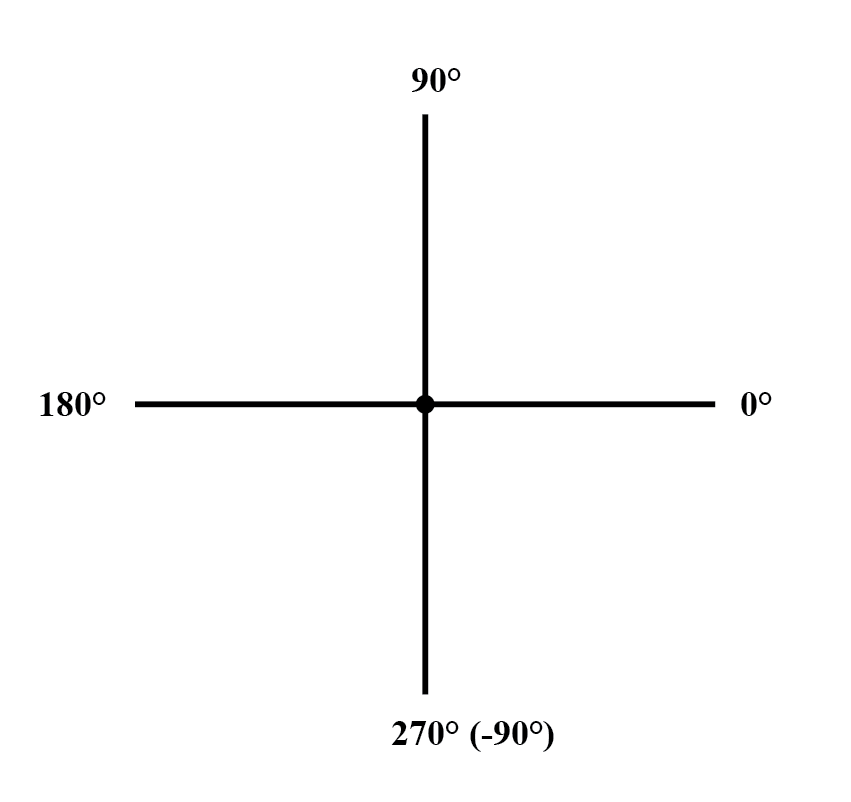
En tant que distances et directions sur une carte, il doit y avoir un cadre de référence commun pour que les chiffres d'angle aient un sens. Dans ce cas, directement à droite est considéré comme 0 ^o , et les angles sont comptés dans le sens positif dans le sens inverse des aiguilles d'une montre :(Figure ci-dessous)

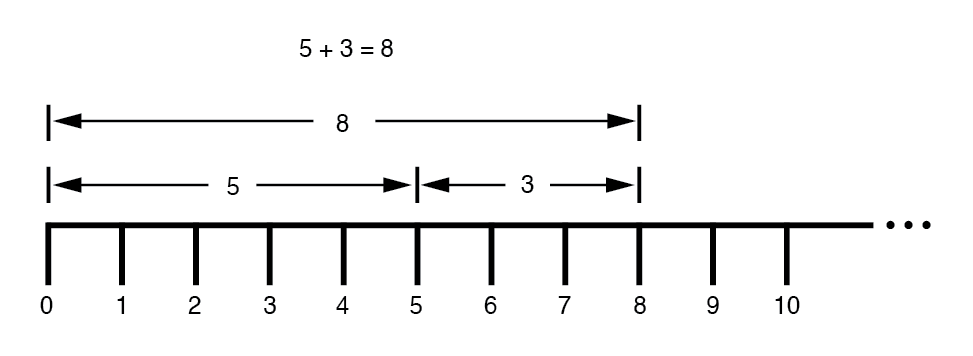
L'idée de représenter un nombre sous forme graphique n'est pas nouvelle. Nous avons tous appris cela à l'école primaire avec la « ligne numérique : » (Figure ci-dessous)

Nous avons même appris comment fonctionnent l'addition et la soustraction en voyant comment les longueurs (magnitudes) s'empilent pour donner une réponse finale :(Figure ci-dessous)

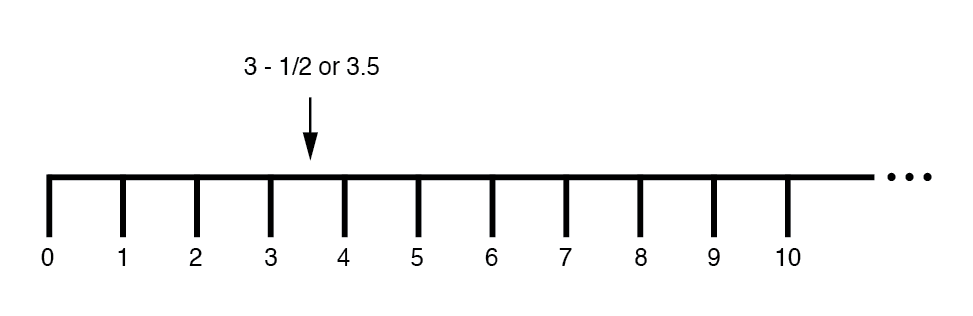
Plus tard, nous avons appris qu'il existait des moyens de désigner les valeurs entre les nombres entiers marqués sur la ligne. Il s'agissait de quantités fractionnaires ou décimales :(Figure ci-dessous)

Ces champs de nombres (entiers, entiers, rationnels, irrationnels, réels, etc.) appris à l'école primaire partagent un trait commun :ils sont tous unidimensionnels . La rectitude de la droite numérique illustre cela graphiquement.

Vous pouvez monter ou descendre sur la droite numérique, mais tous les « mouvements » le long de cette ligne sont limités à un seul axe (horizontal).

Les nombres scalaires unidimensionnels sont parfaitement adaptés pour compter les billes, représenter le poids ou mesurer la tension de la batterie CC, mais ils ne sont pas capables de représenter quelque chose de plus complexe comme la distance et direction entre deux villes, ou l'amplitude et phase d'une forme d'onde AC.

Pour représenter ce genre de quantités, nous avons besoin de représentations multidimensionnelles. En d'autres termes, nous avons besoin d'une droite numérique qui peut pointer dans différentes directions, et c'est exactement ce qu'est un vecteur.

AVIS :

• Un scalaire le nombre est le type d'objet mathématique auquel les gens sont habitués dans la vie de tous les jours :une quantité unidimensionnelle comme la température, la longueur, le poids, etc.
• Un nombre complexe est une quantité mathématique représentant deux dimensions de grandeur et de direction.
• Un vecteur est une représentation graphique d'un nombre complexe. Cela ressemble à une flèche, avec un point de départ, une pointe, une longueur définie et une direction définie. Parfois le mot phaseur est utilisé dans les applications électriques où l'angle du vecteur représente le déphasage entre les formes d'onde.

FICHE DE TRAVAIL CONNEXE :

• Fiche de travail de la phase AC