Absorption parfaite induite par plasma dans le système graphène/métal

Contexte

La plasmonique a attiré une large attention en raison de ses propriétés extraordinaires [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] et de son énorme potentiel dans de nombreux domaines, y compris l'intégration photonique, biodétection, capture d'énergie, photodétection. Récemment, un nouveau phénomène plasmonique, connu sous le nom de plasmons de surface d'usurpation (SSP), a été observé, qui peut se propager à travers les métaux perforés et dépasser la limite de diffraction [16]. Les SSP ont ensuite été explorés dans le THz, les micro-ondes et les gammes de fréquences inférieures [17,18,19], et un certain nombre de dispositifs à sous-longueur d'onde profonds basés sur les SSP ont été proposés et démontrés [20, 21]. Cependant, l'application de tels dispositifs est sérieusement entravée par le taux d'amortissement élevé des SPP. Une solution à ce problème est le milieu de transparence induite par plasmon artificiel (PIT) [22], qui présente une fenêtre de transparence nette dans un large spectre d'absorption. L'effet PIT repose principalement sur le couplage d'un élément radiatif et d'un élément sous-radiant, ce qui a été largement étudié [23,24,25]. Un phénomène similaire, l'absorption induite par les plasmons (AIP), a également été démontré récemment, qui résulte de l'interférence constructive des modes plasmoniques clair et sombre [26]. La résonance PIA [27, 28] peut présenter un effet de lumière remarquablement rapide, qui a des applications potentielles dans la commutation et le traitement optiques.

Cependant, les dispositifs traditionnels basés sur l'effet PIA de la structure métallique sont difficiles ou impossibles à obtenir une accordabilité, ce qui restreint sérieusement ses applications. Le graphène [29, 30], connu pour sa semi-métallicité, sa grande mobilité et sa grande accordabilité, peut être un excellent matériau candidat pour les dispositifs plasmoniques infrarouges accordables. Dans cet article, nous avons étudié un effet PIA accordable, qui est obtenu par l'interférence constructive d'un mode de résonance F-P et d'un mode quasi-guidé soutenus par un sillon d'argent périodique et un graphène monocouche respectivement. On constate que la force de résonance et la largeur de raie dépendent fortement de la distance de couplage. Il est également montré que le taux d'extinction peut atteindre ~ 99,999 %. Le taux d'extinction est défini comme 1-R -T , où R et T sont respectivement la réflectance et la transmittance. C'est simplement 1-R dans notre système puisque la transmittance ici est de 0. En conséquence, un FOM* ultra-élevé pouvant atteindre 10 ⁶ dans le système graphène/métal peut être atteint et la fréquence de résonance peut être réglable dynamiquement en ajustant la tension de grille du graphène. Ces propriétés importantes peuvent être appliquées à la détection biochimique et à la commutation optique dynamique.

Méthodes

Le schéma de notre structure est montré dans la Fig. 1, composé d'un graphène monocouche et d'un Al₂ O₃ couche isolée au-dessus d'un argent rainuré. L'épaisseur de l'Al₂ O₃ est g . Le système est éclairé par une onde plane incidente normale de polarisation magnétique transversale (TM). Les autres paramètres structurels s'expriment comme suit :d est la profondeur de la rainure d'argent ; w est la largeur de la rainure d'argent ; P est la période de la maille unitaire. Dans la région de l'infrarouge moyen, la diffusion intrabande domine dans le graphène hautement dopé, et sa conductivité prend une forme semblable à celle de Drude σ _g =c'est-à-dire ² E _F /[πħ ² (ω +iτ ^-1 )]. Le temps de relaxation électronique est exprimé par τ =μE _F /eυ _F ² , où υ _F =c /300 est la vitesse de Fermi, E _F est l'énergie de Fermi et μ =10 m ² /Vs est la mobilité DC du graphène [25, 31, 32]. Dans les simulations du domaine temporel aux différences finies (FDTD), les constantes optiques pour l'argent et Al₂ O₃ sont de réf. [33] et réf. [34]. Les conditions aux limites périodiques sont utilisées pour simuler des structures cellulaires périodiques infinies. Pour simplifier, nous supposons que le matériau de la région au-dessus de la couche de graphène est le vide (ε ₀ =1).

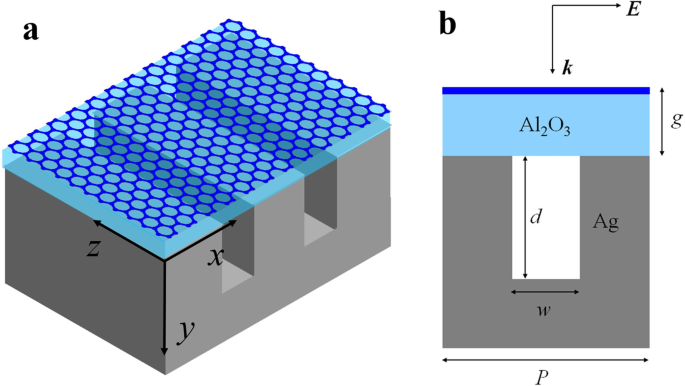
Schéma de principe de la structure graphène-sillon argent. un Vue oblique. b Le schéma en coupe d'une maille élémentaire

Résultats et discussion

Nous avons simulé le spectre de réflexion du sillon d'argent avec w =100 nm, P =250 nm, d =2000 nm, et le résultat est montré sur la figure 2a (courbe rouge). Une forte baisse peut être observée à ~ 28 THz, avec un taux d'extinction ~ 44% et Q facteur ~ 0,8, qui est dû à une résonance F-P induite par le SSP excité par la lumière incidente [19]. Cette résonance a une large gamme de bandes de résonance et donc le mode de résonance peut servir de mode superradiant dans notre système PIA. Ensuite, nous avons calculé le spectre de réflexion de la feuille de graphène avec des conditions aux limites métalliques en bas de la zone de simulation, avec un niveau de Fermi E _F =0,3 eV, comme le montre la figure 2a (courbe bleue). Le spectre de réflexion montre que la résonance plasmon du graphène ne peut pas être directement excitée par l'incidence à cette fréquence. Pour visualiser et optimiser le mode plasmon supporté par le graphène, nous simulons d'abord les modes de résonance supportés par le graphène. Pour éliminer l'impact potentiel de la résonance F-P du sillon d'argent, nous supposons que le sillon est fait de silicium au lieu d'argent. Les spectres de réflectance de la structure ont été calculés pour E _F =0,3 eV et différentes cellules unitaires P et est représenté sur la figure 2b. Un creux de réflectance à la fréquence de résonance f =32,84 THz peut être observé pour P =250 nm avec un Q facteur ~ 304. Le Q élevé la résonance avec une bande de résonance étroite peut servir de mode subradiant (sombre) dans notre système PIA. Le creux de réflectance est dû à la résonance du mode quasi-guidé plasmonique dans le graphène avec l'incidence normale [35] puisque le sillon peut compenser le décalage du vecteur d'onde basé sur le m condition de concordance de phase de e ordre [36, 37]

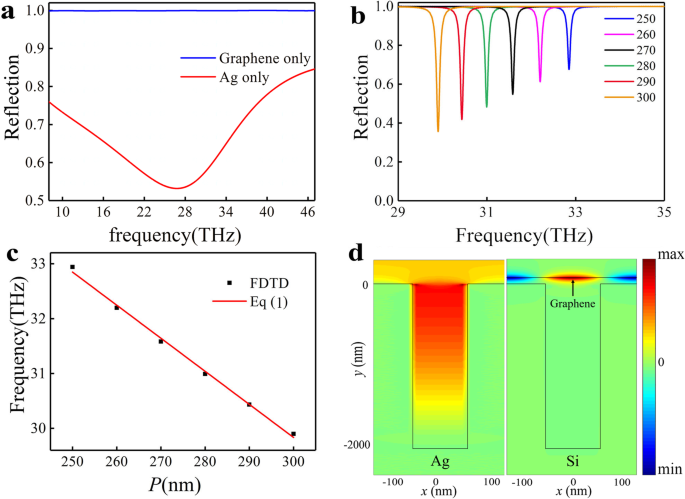
Réponse optique des modes simples. un Les spectres de réflectance de la structure du sillon d'argent uniquement (ligne rouge) et du graphène uniquement (ligne bleue) en incidence normale, respectivement. b Les spectres de réflectance de la structure du sillon graphène-Si pour différentes périodes P de cellule unitaire. c La modélisation numérique et les résultats analytiques de la fréquence de résonance f , respectivement. d Le champ électrique E _x distributions du mode F-P (à gauche) et du mode de résonance quasi-guidé du graphène (à droite).

où k _x =k ₀ péchéθ , k ₀ =2π /λ est le vecteur d'onde dans l'espace libre, θ est l'angle entre la lumière incidente et y -direction, n _eff est l'indice de réfraction effectif du mode guide d'ondes TM dans le graphène, et G _x est le vecteur réseau réciproque du réseau (G _x =2π /P ). Dans la discussion suivante, l'angle de lumière incidente de y -la direction est zéro (θ =0°). La situation pour les autres angles d'incidence est discutée dans le fichier supplémentaire 1. Les positions de ces creux de réflectance correspondent à la fréquence de résonance du mode quasi-guidé dans le graphène, comme le montre la figure 2b. Les résultats de la simulation concordent bien avec l'équation. (1), où m =1 et l'indice de réfraction effectif, ~ 33, est obtenu par des solutions FDTD, comme le montre la figure 2c. Le champ électrique E _x les distributions du mode F-P et du mode quasi-guidé du graphène ont été montrées sur la figure 2d. Il est à noter que le confinement énergétique des modes SSP soutenus par la surface rainurée de Si peut être négligeable par rapport au mode quasi-guidé du graphène.

Dans la situation de couplage, les deux modes propres seront fortement couplés lorsqu'ils se rapprochent l'un de l'autre, et donc le spectre de réflexion sera considérablement modifié. Un dip étroit de sous-largeur de raie d'absorbance améliorée avec un rapport d'extinction ~ 99,97 % est observé au-dessus du dip de réflectance plus large, comme le montre la figure 3a. Lors de l'augmentation de la distance verticale g , le couplage en champ proche et le mode quasi-guidé s'affaiblissent au fur et à mesure que la modulation du creux de réflectance diminue. Il existe deux manières possibles de réduire le creux de réflectance :le couplage le plus faible et l'excitation en mode quasi-guidé plus faible. Par conséquent, nous avons utilisé le modèle d'oscillateur couplé pour comprendre quantitativement le système PIA [38].

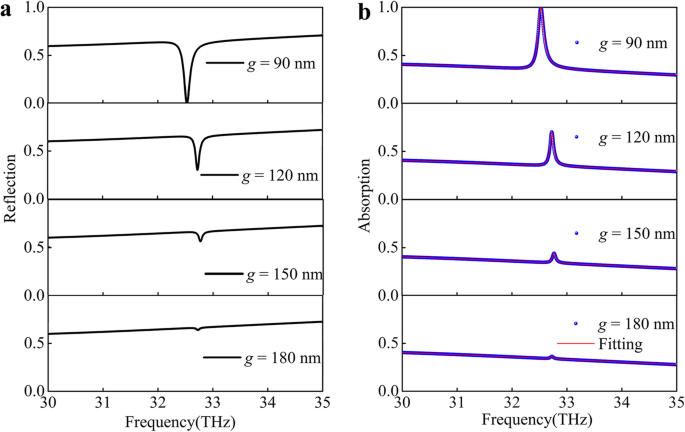
La réponse optique varie avec la distance de couplage. un Le reflet. b Spectres d'absorption de la structure du sillon graphène-argent en incidence normale pour différentes distances g entre le graphène et le sillon d'argent. La courbe noire/les boules bleues sont calculées par la méthode FDTD et la courbe rouge est un ajustement analytique par l'Eq. (3) du dispositif PIA

Où \( {\tilde{a}}_{1,2}={a}_{1,2}\left(\omega \right){\mathrm{e}}^{i\omega t} \) , ω _1,2 et γ _1,2 sont les amplitudes harmoniques temporelles, les fréquences de résonance et les constantes d'amortissement du mode clair et du mode sombre, respectivement. b est le coefficient de couplage mesurant la force du couplage du mode brillant avec le champ électrique incident. \( \tilde{\kappa}=\kappa {e}^{i\varphi} \) est un paramètre de couplage complexe, qui est introduit pour exprimer l'effet de retard de phase. φ est un déphasage, qui est un coefficient clé pour déterminer la forme de l'interférence entre les deux voies cohérentes. Quand φ =0 est un paramètre réel et le comportement typique de l'effet PIT peut être observé, et l'interférence entre les deux voies cohérentes est destructrice. Pour φ =/2 est un paramètre imaginaire pur et l'interférence entre les deux voies cohérentes est convertie de destructrice à constructive [26]. L'absorption du système peut être calculée comme l'énergie dissipée sur la base de la formule (2), qui est

Ensuite, nous ajustons les spectres d'absorption numériques avec l'Eq. (3) pour différents g , qui ont été représentés sur la figure 3b (courbes rouges). Les résultats de la simulation sont en bon accord avec les résultats de la modélisation analytique basée sur le modèle d'oscillateur couplé, ce qui confirme fortement le principe de conception de notre dispositif PIA. Les paramètres d'ajustement κ , φ , γ ₁ , et γ ₂ ont été montrés dans la Fig. 4a–c. Le g croissant donne une diminution du paramètre de couplage κ , comme le montre la figure 4a. En diminuant progressivement le couplage (en augmentant g ), la phase φ est inchangé, et γ ₂ diminue progressivement tandis que γ ₁ changements légèrement montrés dans la Fig. 4b, c. Le paramètre de couplage κ dépasser les constantes d'amortissement du mode sombre γ ₂ pour la distance minimale de gap, ce qui confirme que le couplage du mode clair au mode sombre est plus fort que les processus de dissipation dans la feuille de graphène.

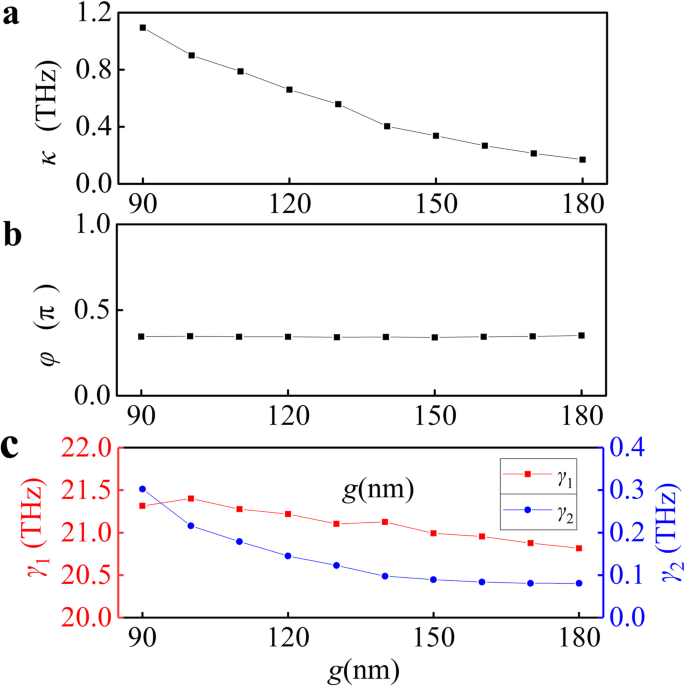
Analyse quantitative des réponses optiques dans les systèmes couplés. Numérique extrait (a ) couplage, (b ) phase, et (c ) coefficients d'amortissement en fonction de l'écart g . Valeurs de κ , φ , et γ ₁ , γ ₂ ont été extraits en ajustant les spectres d'absorption numériques

Pour visualiser l'interférence constructive entre les modes clair et sombre, nous avons étudié l'évolution du champ magnétique de la structure avec le temps, et deux H _z les moniteurs ont été placés à 3 nm du centre du graphène et à 1000 nm du fond de la rainure d'argent, respectivement. La différence de phase oscillante entre les deux modes est de 0,5 , comme indiqué sur la figure 5a. La distribution du champ magnétique à un moment différent a été calculée dans la fréquence de résonance PIA f _q =32,5 THz, où ω _q t ₁ ~ 2,00 et ω _q t ₂ ~ 2.50π, comme indiqué sur la Fig. 5b, c. Le maximum du champ magnétique dans le sillon d'argent peut être observé pour 2,00π tandis que le champ magnétique dans le graphène atteint son maximum pour 2,50π, indiquant le couplage déphasé entre les deux structures. Par conséquent, l'évolution et la formation de la résonance sont déterminées par des interférences constructives [39].

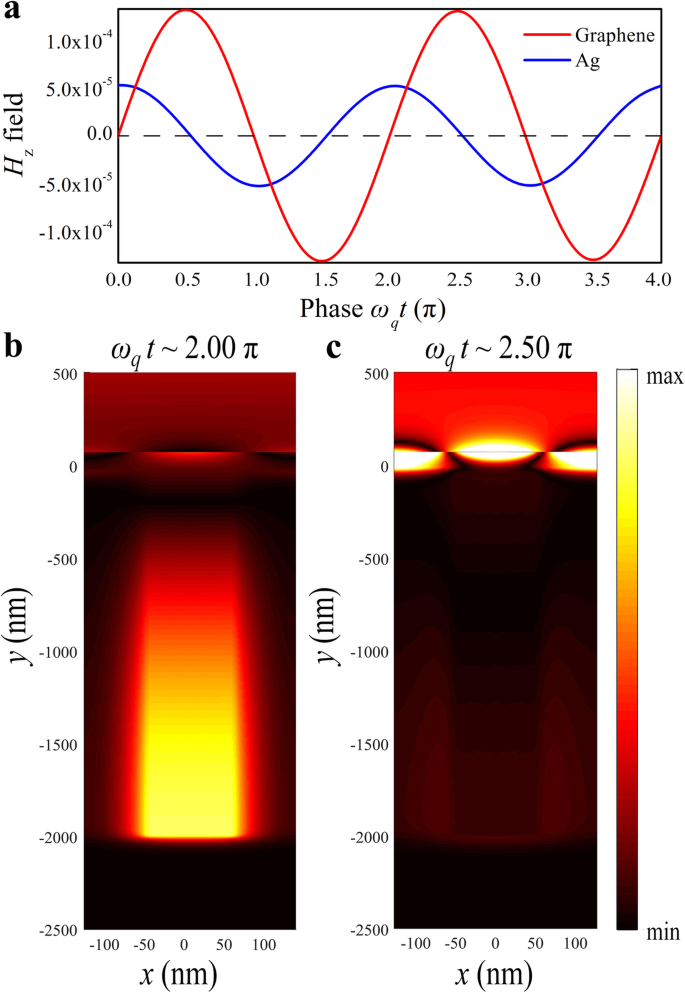
Evolution temporelle des modes couplés. un Evolution temporelle calculée de l'intensité du champ magnétique au niveau du graphène (ligne rouge) et du sillon argenté (ligne bleue). z calculé composante des distributions de champ magnétique pour g =90 nm. L'intensité de champ maximale au sillon d'argent et au graphène est observée à des moments différents b ω _q t ₁ ~ 2.00π et c ω _q t ₂ ~ 2.50π, respectivement

Dans l'application pratique, une bande de réflexion étroite et un rapport d'extinction élevé sont fortement souhaités. Pour réaliser ces deux conditions, on peut ajuster la période de l'unité P et profondeur du sillon argenté d optimiser nos paramètres structurels. Après avoir calculé le spectre de réflexion de différents paramètres de structure P de 1900 à 2100 nm et d de 245 à 265 nm par FDTD, nous obtenons un taux d'extinction très élevé ~ 99,999 % en P =254 nm et d =1980 nm. Le spectre de réflectance du dispositif PIA dans différents environnements d'indice de réfraction est représenté sur la figure 6a. Les capacités de détection sont définies comme [39] :

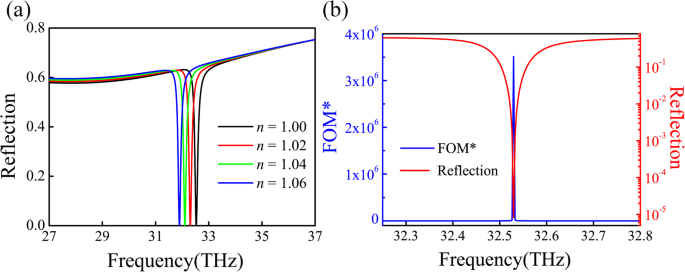
Les performances de détection du système. un La réponse de détection du capteur PIA pour un environnement diélectrique varié. b La courbe FOM* associée et les spectres de réflectance

où f et Je sont respectivement la fréquence de résonance et l'intensité spectrale. Lors de la mesure de l'intensité de réflexion d'un capteur, la capacité de sensibilité du capteur peut être quantifiée par la valeur FOM*. Plus la valeur est élevée, plus la sensibilité du capteur est élevée. A partir de la figure 6a, nous pouvons obtenir S =11,2 THz/RIU et le FOM ~ 94,1 associé, avec la pleine largeur à mi-hauteur (FWHM) ~ 30 nm (0,12 THz). Ce FOM est supérieur à la valeur des absorbeurs de métamatériaux basée sur la résonance du réseau de surface. De plus, notre capteur PIA peut conduire à une valeur FOM* ultra élevée de 3,5 × 10 ⁶ , comme indiqué sur la figure 6b. Nous avons comparé les performances des capteurs récemment étudiés dans le Fichier Additionnel 1 :Tableau S1.

Dans le système PIA, le graphène joue un autre rôle clé. La modulation de la fréquence de résonance peut être obtenue en réglant la tension de déclenchement pour ajuster le niveau de Fermi du graphène. Les spectres simulés sont présentés dans les fichiers supplémentaires 2 :Figure S1 et 3 :Figure S2. Le contrôle actif de décalage de fréquence de la résonance PIA est significatif pour le capteur ou l'absorbeur.

Conclusions

En résumé, nous avons démontré numériquement l'absorption parfaite induite par l'interférence constructive entre le mode de résonance F-P et le mode quasi-guidé plasmonique du graphène. Grâce à l'introduction du mode quasi-guidé plasmonique du graphène, nous obtenons la raie spectrale avec une largeur de raie plus étroite du mode de résonance F-P du sillon d'argent. Lorsque la distance g augmente progressivement, la force de résonance et la largeur de ligne diminuent. Pour l'application, le FOM* dans notre système peut atteindre 10 ⁶ . De plus, la fenêtre d'absorption peut être ajustée en faisant varier le paramètre géométrique et le niveau de Fermi de graphène. Ces résultats pourraient fournir une nouvelle voie vers la réalisation d'un contrôle spectral dynamique dans l'infrarouge moyen à l'échelle nanométrique et de capteurs optiques ultrasensibles.

Disponibilité des données et des matériaux

Toutes les données générées ou analysées au cours de cette étude sont incluses dans cet article publié [et ses fichiers d'informations supplémentaires].

Abréviations

FDTD :

Domaine temporel aux différences finies

FOM* :

Figure du mérite*

F-P :

Fabry-Pérot

FWHM :

Pleine largeur à mi-hauteur

PIA :

Absorption induite par le plasmon

PIT :

Transparence induite par le plasmon

Q facteur :

Facteur de qualité

SSP :

Usurpation des plasmons de surface

TM :

Magnétique transversale