Observation de l'effet Hall de spin inverse photo-induit extrinsèque dans un gaz d'électrons bidimensionnel GaAs/AlGaAs

Contexte

La spintronique a attiré beaucoup d'attention en raison de ses applications potentielles dans les technologies de l'information ainsi qu'en révélant des questions fondamentales sur la physique du spin des électrons dans la matière condensée [1–4]. L'effet Hall de spin (SHE) et sa réciproque Onsager, l'effet Hall de spin inverse (ISHE), jouent un rôle important en spintronique car ils fournissent une méthode électrique pour convertir le courant de charge en courant de spin et vice versa, via un couplage spin-orbite ( SOC) [2, 5–8]. Le SHE et l'ISHE ont été largement étudiés dans les films métalliques avec des éléments lourds, tels que Pt, Ta, Py et IrMn, et les isolants topologiques émergents, tels que Bi₂ Se₃ et SnTe, en raison de leur fort SOC [9–14]. Ces deux effets sont également observés dans les semi-conducteurs, tels que le gaz d'électrons bidimensionnel GaAs, ZnO, Si, Ge, GaN/AlGaN et GaAs/AlGaAs [15–20].

La conversion du courant spin-charge dans les semi-conducteurs est un enjeu important, car elle ouvre la voie à l'intégration de la spintronique à l'électronique [5]. L'ISHE photo-induit (PISHE) est récemment devenu un outil expérimental efficace pour étudier l'ISHE dans les semi-conducteurs, qui exploite une lumière polarisée circulairement avec une distribution gaussienne pour introduire un courant de spin dans les semi-conducteurs, puis utilise l'ISHE pour générer un courant de charge. 2, 19–22]. Le courant PISHE peut être observé à température ambiante et offre un moyen pratique d'étudier l'ISHE des semi-conducteurs sans introduire de champ magnétique et d'éléments ferromagnétiques [20]. En outre, le PISHE ouvre également la voie à la conception de nouveaux types de dispositifs de spin-photonique [22]. Le courant PISHE a été observé dans les hétérostructures GaN/AlGaN, GaAs/AlGaAs et MgZnO/ZnO [2, 19, 20]. Cependant, la dépendance du courant PISHE sur la puissance lumineuse et le profil lumineux est encore inconnue.

Il existe deux mécanismes pour ISHE, à savoir, intrinsèque et extrinsèque. Le mécanisme intrinsèque ne dépend que de la structure de bande du matériau parfaitement ordonné [7, 23, 24], provenant de Rashba [25-27] ou Dresselhaus SOC [26], tandis que le mécanisme extrinsèque fait référence à un Mott-skew ou latéral asymétrique. -saut de diffusion à partir d'impuretés dans un système couplé spin-orbite [16, 24, 28, 29]. Bien qu'il existe de nombreuses études sur le mécanisme intrinsèque ou extrinsèque de l'ISHE, la plupart d'entre elles sont des travaux théoriques, et très peu de travaux expérientiels se concentrant sur cette question [16, 27, 30–32], car il est très difficile de distinguer ces deux mécanismes expérimentalement.

Dans cet article, nous étudions le courant PISHE dans un gaz d'électrons bidimensionnel GaAs/AlGaAs (2DEG). On constate que le courant PISHE augmente avec l'augmentation de la température, indiquant que le courant PISHE est principalement dominé par le mécanisme extrinsèque. Cette inférence est encore confirmée par la faible dépendance du courant PISHE vis-à-vis de l'orientation cristalline de l'échantillon. En outre, nous étudions également la dépendance du courant PISHE sur la puissance lumineuse et le profil lumineux, ce qui est très en accord avec le modèle théorique.

Méthodes

L'expérience est réalisée sur un échantillon GaAs/AlGaAs 2DEG dopé modulation orienté (001) cultivé par épitaxie par jets moléculaires (MBE) sur un substrat GaAs semi-isolant. La densité électronique et la mobilité Hall de l'échantillon sont mesurées à 5,18 × 10 ¹¹ cm ⁻² et 3,97 ×  10 ³ cm ² V ⁻¹ s ⁻¹ à température ambiante, respectivement. La mobilité du 2DEG est un peu faible en raison du dopage de fond, qui est de l'ordre de 10 ¹⁵ ou 10 ¹⁶ cm ⁻³ , dans l'échantillon introduit lors de la croissance de l'échantillon. L'échantillon est clivé dans les directions [110] et \([1\bar {1}0]\) en un carré de 10 × 10 mm ² . Deux paires de contacts ohmiques distants de 8 mm dans les directions [110] et [100], respectivement, sont réalisées par dépôt d'indium et recuites à environ 420 °C dans une atmosphère d'azote.

Un laser à solide pompé par diode avec une longueur d'onde de 1064 nm est utilisé comme source de rayonnement. Le faisceau laser traverse un hacheur, un polariseur et une lame quart d'onde et illumine enfin l'échantillon verticalement. Ici, le polariseur et la lame quart d'onde rotative sont utilisés pour modifier l'hélicité lumineuse P _c =sin2φ de gaucher (σ ⁻ , P _c =− 1) à droitier (σ ⁺ , P _c =+ 1) en continu, où φ est l'angle entre la direction de polarisation de la lumière incidente et l'axe optique de la lame quart d'onde. La tache lumineuse sur l'échantillon a un profil gaussien. Le courant est collecté entre les deux contacts dans le sens [100] (ou [110]) de l'échantillon par un préamplificateur et un amplificateur de verrouillage avec une fréquence de référence de 229 Hz à partir du hacheur. La figure 1a illustre le montage utilisé pour mesurer le courant PISHE.

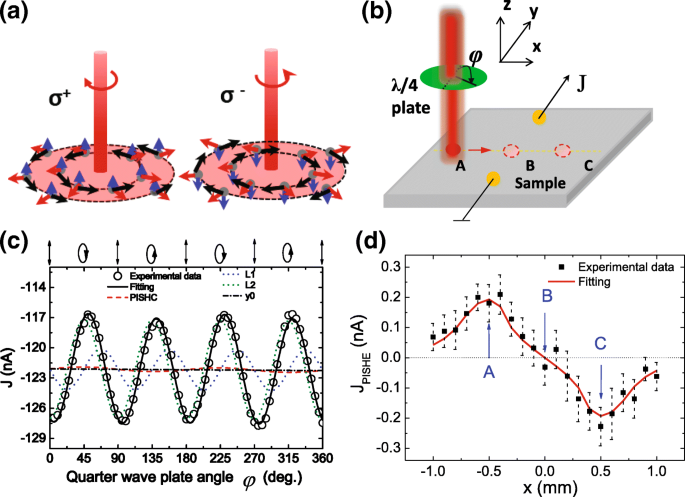
Méthode pour obtenir le courant PISHE et le PISHE mesuré à 300 K. a Illustration du mouvement des électrons polarisés en spin sous l'éclairage normal de la polarisation circulaire gauche (σ ⁺ ) ou polarisation circulaire droite (σ ⁻ ) lumière. Les flèches rouges indiquent le flux d'électrons, les flèches bleues indiquent la direction de spin des électrons et les flèches noires montrent la force transversale de spin agissant sur les électrons. b La géométrie utilisée pour mesurer le courant PISHE. c Le photocourant mesuré à 300 K en fonction de l'angle de phase φ sous incidence normale lorsque la tache lumineuse est illustrée au point A. La ligne continue (noir) est la courbe d'ajustement utilisant l'Eq. (1), la ligne pointillée (rouge) représente le courant PISHE, et les lignes pointillées bleue et verte représentent le L ₁ et L ₂ composant. La ligne pointillée indique le courant de fond J ₁ . d Le courant PISHE en fonction des emplacements des spots lumineux mesurés à 300 K

Pour les mesures dépendantes de la puissance, la puissance de la lumière irradiée sur l'échantillon est modifiée de 250 à 40 mW en utilisant des atténuateurs. Pour modifier le profil de la tache lumineuse sur l'échantillon, une lentille optique avec différentes distances focales est adoptée. Dans les mesures dépendantes de la température, l'échantillon est monté sur un cryostat optique, qui permet la variation de température de 77 à 300 K.

Pour obtenir le rapport relatif de Rashba à Dresselhaus SOC, nous mesurons le photocourant induit par effet photogalvanique circulaire (CPGE) pour différentes directions cristallographiques, c'est-à-dire que le courant CPGE est collecté le long des directions [110] et [100] à travers les contacts, respectivement, avec le plan incident de la lumière perpendiculaire à la connexion des deux contacts. Pour la mesure CPGE, un montage expérimental similaire à celui utilisé dans la mesure PISHE est adopté sauf que la lumière irradie obliquement sur le milieu de la connexion des deux contacts selon les directions [110] ou [100], et les gammes d'angle d'incidence de − 40 à 40°. Le courant CPGE à un certain angle d'incidence est extrait en ajustant le photocourant dépendant de l'état de polarisation de la lumière J recueillies le long des deux contacts à l'équation suivante [33] :J =J _CPGE sin2φ +L ₁₁ sin4φ +L ₂₂ cos4φ +J ₁₁ . Ici, J _CPGE est le courant CPGE, L ₁₁ et L ₂₂ sont le photocourant induit par la lumière polarisée linéairement, et J ₁₁ est le courant de fond provenant de l'effet photovoltaïque ou effet Dember [33].

Résultats et discussion

Sous un éclairage d'une lumière polarisée circulairement avec un profil gaussien, des porteurs polarisés en spin avec une distribution gaussienne dans l'espace seront générés dans la zone d'absorption non saturée. En conséquence, un courant de spin diffus apparaît qui circule le long de la direction radiale. Ensuite, en raison de l'effet ISHE, les porteurs polarisés en spin subissent une "force transversale de spin" le long de la direction tangentielle, conduisant à un courant de charge transverse, c'est-à-dire un courant vortex (appelé courant PISHE), dans la direction axiale [8, 20], comme le montre la figure 1a. Lorsque l'état de polarisation de la lumière est modifié par rapport à la polarisation circulaire gauche (σ ⁺ ) à la polarisation circulaire droite (σ ⁻ ), la polarisation de spin des électrons est modifiée de spin up à spin down, conduisant à l'inversion de la force transverse de spin et du courant PISHE. Lorsque la lame quart d'onde tourne de 0 à 180°, c'est-à-dire que l'angle φ passe de 0 à 180°, l'état de polarisation de la lumière passe de polarisation linéaire verticale (à 0°), à polarisation circulaire gauche (à 45°), polarisation linéaire verticale (à 90 °), polarisation droite une polarisation circulaire (à 135°), et à nouveau une polarisation linéaire verticale (à 180°) séquentiellement, comme indiqué dans la partie supérieure de la figure 1c. Par conséquent, comme l'angle φ passe de 45 à 135°, le PISHE est inversé, indiquant que le PISHE est proportionnel à sin2φ . Il convient de noter que, lors d'un φ angle de 0, 90 et 180°, la lumière est polarisée linéairement. La lumière polarisée linéairement induira également un photocourant en raison de l'effet d'alignement du moment optique [34], nommé L ₁ , ou en raison de l'absorption optique d'anisotropie [35, 36], appelée L ₂ . Les courants L ₁ et L ₂ induits par la lumière polarisée linéairement sont proportionnels à sin4φ et cos4φ , respectivement. En plus, un fond photocourant J ₁ provenant de l'effet photovoltaïque ou effet Dember sera également présent, qui est indépendant de l'état de polarisation de la lumière. Ainsi, selon leur dépendance différente à l'angle φ , nous pouvons extraire le courant PISHE en ajustant le photocourant J dépendant de l'état de polarisation de la lumière mesuré expérimentalement à la formule suivante [8, 33] :

où J _PISHÉ est le courant PISHE excité par la lumière de polarisation circulaire gauche, L ₁ et L ₂ sont le photocourant induit par la lumière polarisée linéairement, et J ₁ est le courant de fond [19]. Il est à noter que le L ₂ terme a été inclus dans l'équation d'ajustement, c'est-à-dire Eq. (1), en raison de la grande anisotropie optique présente dans l'échantillon. L'anisotropie optique pourrait être induite par des structures d'interface anisotropes [37], la ségrégation des atomes [38] ou la contrainte résiduelle [39].

Pour obtenir la distribution spatiale du PISHE, nous balayons le spot laser de gauche à droite des deux contacts le long de leur médiatrice [voir Fig.1a]. A chaque position de spot, nous faisons tourner la lame quart d'onde de 0 à 360° et obtenons le courant PISHE en adaptant l'Eq. (1) au photocourant J dépendant de l'état de la lumière mesurée expérimentalement . La figure 1b montre un résultat typique de photocourant mesuré en fonction de l'angle de phase φ , lorsque le spot laser est fixé à x =− 0,5 mm, c'est-à-dire au point A [voir Fig. 1a]. Le photocourant est mesuré à 300 K et collecté le long des deux contacts suivant la direction [110]. Le spot laser sur l'échantillon a un diamètre d'environ 1,4 mm avec un profil gaussien et une puissance de 250 mW. Les cercles de la Fig. 1b sont les données expérimentales, et la ligne continue est le résultat d'ajustement selon l'Eq. (1). On peut voir que le photocourant mesuré expérimentalement fluctue périodiquement avec la rotation de la lame quart d'onde. En effet, le photocourant est une somme du courant PISHE, du photocourant induit par la lumière polarisée linéairement et du courant de fond, et ils montrent une dépendance différente de l'angle φ . La ligne pointillée indique le courant PISHE et la ligne pointillée indique le courant de fond. Les lignes pointillées bleues et vertes représentent le L ₁ et L ₂ composante induite par la lumière polarisée linéairement, respectivement. On peut voir que le courant PISHE est beaucoup plus petit que celui du photocourant induit par la lumière polarisée linéairement.

Le courant PISHE obtenu en fonction du spot est représenté sur la figure 1c. On peut voir que, lorsque le spot laser est déplacé de gauche à droite des deux contacts, le courant PISHE inverse sa direction. Lorsque le spot laser est focalisé sur le milieu des deux contacts, le courant PISHE est presque égal à zéro. Ce phénomène peut être expliqué quantitativement par un modèle de courant vortex induit par effet Hall de spin inverse photo-induit [20]. Plus précisément, sous le rayonnement d'un laser à profil gaussien G (r )=\(\frac {1}{\sqrt {2\pi }\sigma }\exp \left (-\frac {r^{2}}{2\sigma ^{2}}\right)\), un courant de spin circulant le long de la direction radiale sera induit, ce qui peut être exprimé par j _r =τ _s D ∇_r G (r ). Ici, D est le coefficient de diffusion de spin, τ _s est le temps de relaxation du spin, r désigne la direction radiale, et σ indique la variance de distribution liée à la pleine largeur à mi-hauteur (FWHM) de l'intensité lumineuse. En raison de l'effet ISHE, les porteurs polarisés en spin subiront une force transversale de spin \(f(r)\propto j_{r}\times \hat {z}\) [20, 40], qui peut être exprimée par \( f(r)=-f_{0}r/\sigma ^{3}\exp \left (-\frac {r^{2}}{2\sigma ^{2}}\right)\). Ici, f ₀ est la constante de force transversale de spin associée au SOC du système matériel. Le champ électrique tourbillonnaire \(\vec {E}\) peut être déterminé par la force électromotrice circulaire (FEM), qui peut être écrite comme \(\varepsilon (r_{0})=\frac {2\pi }{q }\int _{0}^{r_{0}} f(r)rdr\), à \(\oint \vec {E}(r_{0})\cdot d\vec {l}=\varepsilon ( r_{0})\). Ici, r ₀ est le rayon de la tache lumineuse, et la boucle intégrale est le long du périmètre de la tache lumineuse. Par conséquent, nous avons

Il convient de noter que la petite différence entre l'Eq. (2) et celle rapportée dans [20] est due au fait que la fonction gaussienne normalisée est adoptée dans cet article, tandis que la fonction gaussienne non normalisée a été utilisée dans [20]. Le f ₀ dans cet article est équivalent à f ₀ /σ rapporté dans [20]. Le courant électrique entre les deux contacts (appelé a et b , respectivement) peut être exprimé sous la forme

où V _ab (R _ab ) est la tension (résistance) entre les contacts a et b , o est l'origine de la tache lumineuse, et S indique la zone triangulaire de abo . Il convient de mentionner que la zone saturée d'absorption, dans laquelle l'intensité lumineuse absorbée par l'échantillon est constante et atteint l'absorption maximale de l'échantillon, doit être déduite de l'intégrale de l'Eq. (3). Cela est dû au fait que le gradient des porteurs photo-générés est nul dans cette zone, et par conséquent, le courant de spin et le courant PISHE sont tous nuls dans la zone.

Il convient de noter que l'Éq. (3) n'est valable que lorsque les contacts a et b sont couverts par la tache lumineuse, car en dehors de la tache lumineuse Eq. (2) n'est plus valable. Ainsi, compte tenu de la relation entre le courant électrique extérieur (J _f ) et à l'intérieur (J _e ) l'endroit, c'est-à-dire J _f =\(J_{e}\exp \left (-\frac {l}{A\cdot L_{s}}\right)\) [41], on peut exprimer l'Eq. (3) comme :

Ici, l est la distance entre le bord du spot lumineux et la connexion des deux contacts, L _s est la longueur de diffusion des électrons, et A est une constante. En utilisant les équations. (2) et (4) pour s'adapter au courant PISHE mesuré expérimentalement, nous pouvons obtenir la force transversale de spin f ₀ et la longueur de diffusion A ·L _s . Le résultat de l'ajustement est représenté sur la figure 1c par une ligne continue. On peut voir que les données expérimentales sont bien ajustées par le modèle. Dans l'ajustement, les paramètres mesurés expérimentalement suivants sont adoptés, σ =0,2 mm, L =4 mm, r ₀ =0,7 mm, et R _ab =15,5 k Ω . La force transversale de rotation f ₀ /q d'électrons est ajusté à 6,8 × 10 ⁻⁶ N ·m/C à 300 K, A ·L _s est ajusté pour être 2,8 × 10 ⁻⁴ m, et le rayon de la zone saturée d'absorption est ajusté à 0,34 mm, ce qui indique que l'intensité saturée d'absorption de la lumière I _c correspond à environ un cinquième de l'intensité maximale I _m , c'est-à-dire, Je _c =1/5 Je _m .

Pour étudier la dépendance du courant PISHE sur la puissance lumineuse et sur le profil lumineux, nous effectuons la mesure PISHE sous différentes puissances lumineuses et différents profils lumineux. La figure 2a, b montre le courant PISHE en fonction des emplacements des spots lumineux sous différentes puissances lumineuses avec un rayon de spot lumineux de r ₀ =1,5 mm et σ =0,5 mm et r ₀ =1 mm et σ =0,3 mm, respectivement. Les symboles sont les données expérimentales, et les lignes pleines sont les calculs théoriques selon les Eqs. (2) et (4). Dans les calculs, les mêmes paramètres, à l'exception des paramètres du spot lumineux, adoptés sur la figure 1c sont utilisés, c'est-à-dire f ₀ /q =6,8 × 10 ⁻⁶ N ·m/C, A ·L _s =2,8 × 10 ⁻⁴ m, R _ab =15,5 k Ω , et Je _c =1/5 Je _m . Ici, Je _m est l'intensité lumineuse maximale de la lumière lorsque la puissance est de 250 mW. On peut voir que l'intensité du courant PISHE augmente avec la puissance lumineuse, et sous la puissance de 250 mW, la tache lumineuse avec une plus grande FWHM (c'est-à-dire, une plus grande σ ) conduit à un courant PISHE plus important. Nous pouvons également voir que, pour un point lumineux avec une FWHM plus grande, le pic de la courbe PISHE se présentera à une valeur plus grande de x . Ici, x est la distance entre le centre du spot lumineux et le milieu de la connexion des deux contacts. En effet, le courant de spin et le courant PISHE résultant sont proportionnels au gradient du profil lumineux. Pour une meilleure comparaison du courant PISHE induit par différents profils de spots lumineux, nous résumons les résultats de la Fig. 2a, b sur la Fig. 2c, c'est-à-dire que nous résumons la dépendance de la valeur de crête du courant PISHE sur la puissance d'excitation pour différents profils de points lumineux sur la figure 2c, où les symboles indiquent les données expérimentales, et les lignes pleines sont les résultats des calculs théoriques. On peut voir que les résultats expérimentaux concordent très bien avec les simulations théoriques, ce qui confirme le modèle.

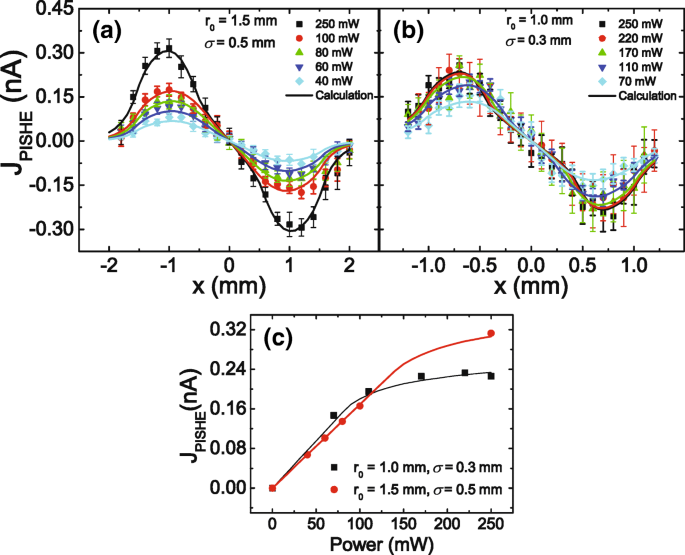
Courant PISHE en fonction des emplacements des spots lumineux sous différentes puissances lumineuses. un , b Courant PISHE excité par une tache lumineuse à profil gaussien avec r ₀ =1,5 mm et σ =0,5 mm et r ₀ =1 mm et σ =0,3 mm, respectivement. c La variation de la valeur crête du courant PISHE avec la puissance d'excitation, dans laquelle les symboles et les traits pleins sont respectivement les données expérimentales et les résultats des calculs théoriques

La figure 2c indique qu'à mesure que la puissance augmente, le courant PISHE augmente d'abord de façon monotone, puis devient progressivement à saturation. L'apparition de la saturation du courant PISHE à puissance lumineuse est due à la présence d'une saturation d'absorption à forte puissance. Lorsque l'intensité lumineuse maximale est inférieure à l'intensité de saturation d'absorption, le courant PISHE augmente linéairement avec la puissance lumineuse. Lorsque l'intensité lumineuse maximale est supérieure à l'intensité de saturation d'absorption, le courant PISHE tend à saturer avec l'augmentation de la puissance lumineuse. L'influence de la taille du spot lumineux sur le courant PISHE peut être comprise dans l'aspect de l'effet du FWHM du spot lumineux sur le courant PISHE, car la taille du spot lumineux et le FWHM sont corrélés l'un à l'autre par la puissance lumineuse. Plus précisément, pour une certaine puissance lumineuse, une plus grande taille de tache lumineuse a une plus grande valeur de FWHM. À une certaine puissance lumineuse, si l'intensité lumineuse maximale est inférieure à l'intensité de saturation d'absorption, un profil lumineux avec un FWHM plus petit (c'est-à-dire une plus petite taille de tache lumineuse) peut générer un courant PISHE plus important, car un FWHM plus petit entraînera un plus grand courant de rotation ; tandis que si l'intensité lumineuse maximale est supérieure à l'intensité de saturation d'absorption, un profil lumineux avec une valeur FWHM plus petite conduira à un courant PISHE plus petit. Cela peut également être clairement vu sur la figure 3, qui résume le courant PISHE en fonction des emplacements des spots lumineux sous différents profils lumineux. La puissance de la lumière est de 250 mW. On peut voir que, comme la valeur de σ augmente de 0,2 à 0,5 mm, la valeur de crête du courant PISHE diminue de façon monotone. En effet, dans la zone saturée d'absorption, il n'y a pas de courant de spin et, par conséquent, aucun courant PISHE n'est généré. Par conséquent, la lumière à l'intérieur de la zone saturée d'absorption n'apporte aucune contribution au courant PISHE. L'encart de la figure 3 montre la distribution de l'intensité lumineuse pour différents profils lumineux gaussiens. La ligne en pointillés représente l'intensité de saturation d'absorption de l'échantillon. Les points d'intersection entre la ligne pointillée et les courbes d'intensité lumineuse indiquent le rayon des zones saturées d'absorption, notées r _s . La lumière dans la zone circulaire de rayon r _s , qui est indiqué par la zone d'ombre lorsque r ₀ =1.5 et σ =0,5 mm, ne contribue pas au courant PISHE. On peut voir que, pour une puissance lumineuse de 250 mW, bien qu'un profil lumineux avec un FWHM plus petit conduira à un courant de spin plus important dans la zone d'insaturation d'absorption, cet effet est dépassé par la plus grande quantité d'énergie gaspillée dans la zone de saturation d'absorption. En conséquence, le profil de lumière avec une valeur inférieure de σ (c'est-à-dire, σ =0,2 mm) génère une valeur de PISHE plus petite que celle avec un σ plus grand (c'est-à-dire, σ =0,3 ou 0,5 mm).

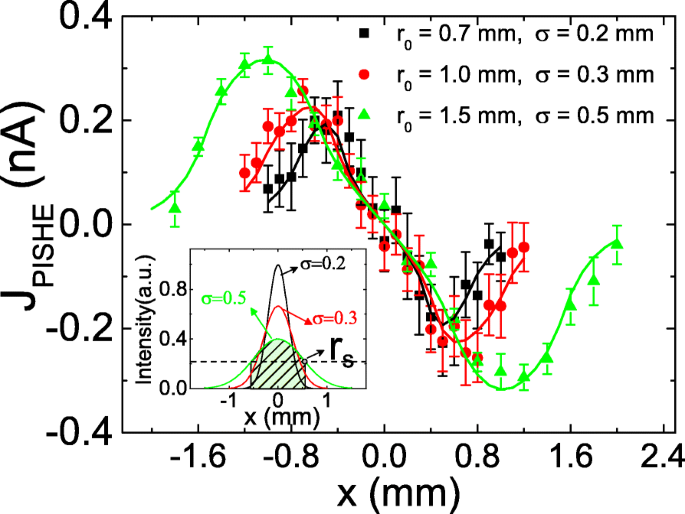
Courant PISHE en fonction de l'emplacement du spot lumineux sous différents profils lumineux gaussiens lorsque la puissance lumineuse est de 250 mW. L'encart montre la distribution de l'intensité lumineuse pour différents profils lumineux gaussiens. La ligne pointillée indique l'intensité de saturation d'absorption de l'échantillon

Pour étudier le mécanisme dominant du PISHE, nous effectuons les mesures PISHE à différentes températures. La figure 4a montre le courant PISHE en fonction de l'emplacement du spot lumineux mesuré à 77, 130, 180 et 230 K. Le spot laser a un profil gaussien avec r ₀ =0,7 mm et σ =0,2 mm, et la puissance est de 250 mW. Les carrés indiquent les données expérimentales et les lignes pleines sont les résultats d'ajustement à l'aide des équations. (2) et (4). On peut voir que les données expérimentales sont toutes bien ajustées par le modèle à toutes les températures. Par l'ajustement, on peut obtenir l'effort transversal de spin f ₀ /q , qui est montré dans la Fig. 4b, et la longueur de diffusion des électrons A ·L _s à différentes températures. La ligne pointillée sur la figure 4b est le guide pour les yeux. Pour déterminer la valeur du paramètre A , nous devrions comparer la dépendance à la température de A ·L _s aux résultats précédents de la dépendance à la température de la longueur de diffusion des électrons L _s . En adaptant notre valeur de A ·L _s à la valeur de L _s obtenu dans [42], on peut déterminer la constante A être de 1,65 × 10 ² . Le très bon accord de nos résultats avec les résultats précédents montrés sur la figure 4c vérifie notre méthode. On peut voir que la longueur de diffusion des électrons diminue avec l'augmentation des températures, ce qui peut être principalement attribué à l'amélioration de la diffusion des porteurs par les phonons [43].

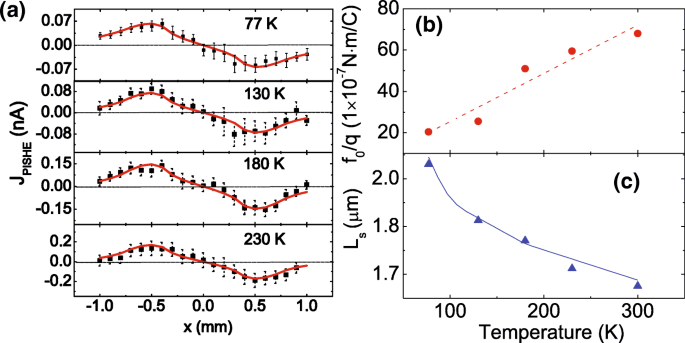
Dépendance en température du courant PISHE, de la force transversale de spin et de la longueur de diffusion des électrons du GaAs/AlGaAs 2DEG. un Résultats expérimentaux et de modélisation du courant PISHE en fonction des emplacements des spots lumineux mesurés à différentes températures. Les carrés pleins sont les données expérimentales, et les lignes pleines sont les résultats d'ajustement. b , c Force transversale de spin et longueur de diffusion des électrons en fonction de la température, respectivement. La ligne pointillée dans b est le guide pour les yeux, et la ligne continue en c est obtenu à partir de [42]

Étonnamment, la force transversale de rotation f ₀ /q du 2DEG augmente de façon monotone avec l'augmentation de la température, ce qui montre une tendance de variation inverse de la température pour le PISHE observé dans les structures hybrides Au/InP [44]. Ce phénomène inattendu peut être lié au mécanisme de PISHE. Il existe deux mécanismes pour le PISHE dans le semi-conducteur 2DEG, à savoir les mécanismes intrinsèques et extrinsèques. Le premier provient principalement de la structure de bande, et le dernier provient des asymétries de diffusion pour les spins ascendants et descendants dues à l'effet SOC dans les impuretés [7, 16]. Pour un semi-conducteur 2DEG de C _2v symétrie du groupe ponctuel, la force transversale de spin induite par le mécanisme intrinsèque peut être exprimée sous la forme \(f_{0}=\frac {4m^{*2}\tau _{s}D}{\hbar ^{2}}\left (\alpha ^{2}+\beta ^{2}\right)\) [20, 40], où \(\hbar \) est la constante de Planck réduite, τ _s est le temps de relaxation du spin, D est le coefficient de diffusion de spin, et α (ou β ) est la constante de Rashba (ou Dresselhaus) qui est proportionnelle à la force de Rashba (ou Dresselhaus) SOC. Pour un GaAs/AlGaAs 2DEG, le temps de relaxation de spin τ _s est proportionnel à T ⁻¹ [45]. Ici, T représente la température. Pour la modulation dopée 2DEG, la force de Rashba SOC est beaucoup plus grande que celle de Dresselhaus (voir la discussion suivante); en conséquence, la constante de Rashba α est beaucoup plus grande que la constante de Dresselhaus β . Le coefficient de diffusion de spin D est proportionnel à T ⁻² [46, 47]. La dépendance à la température de α peut être exprimé par a +b T , où a et b sont des constantes, et a est d'environ deux commandes supérieures à b [48]. Ainsi, en tenant compte de la dépendance à la température de τ _s , D , et α , nous avons f ₀ ∝T ⁻³ , ce qui suggère que la force transversale de spin induite par le mécanisme intrinsèque devrait diminuer avec l'augmentation des températures. Pour le mécanisme extrinsèque, la force transversale de spin dépend de la concentration d'impureté ionisée, en particulier pour la diffusion latérale extrinsèque [49, 50]. Étant donné qu'il y a un dopage de fond dans notre échantillon et que l'ionisation des impuretés augmente avec l'augmentation de la température, une plus grande diffusion d'asymétrie pour les électrons de spin-up et de spin-down se produit lorsque la température augmente, conduisant à une force transversale de spin plus importante avec l'augmentation de la température. Étant donné que la force transversale de rotation f ₀ observé dans notre expérience augmente avec l'augmentation de la température, on peut en déduire que le PISHE est dominé par le mécanisme extrinsèque, dans lequel les impuretés sont principalement introduites par le dopage de fond au cours du processus de croissance.

Pour confirmer davantage que le PISHE est bien dominé par le mécanisme extrinsèque, nous mesurons la distribution spatiale du courant PISHE collecté le long de différentes directions cristallines. La figure 5a, b montre la distribution spatiale du courant PISHE collecté le long des directions cristallines [110] et [100], respectivement. Pour éliminer l'influence de la mobilité des porteurs et de la densité des porteurs dans différentes directions cristallines, nous normalisons le courant PISHE par le photocourant correspondant J ₀ sous une polarisation de 0,3 V lorsque les contacts sont dans les directions [110] et [100], respectivement. Les mesures sont effectuées à température ambiante sous un rayonnement de puissance 60 mW. Le rayon du spot lumineux r ₀ est de 1,0 mm, et σ est de 0,3 mm. Les symboles indiquent les données expérimentales et les lignes pleines sont les résultats d'ajustement selon les équations. (2) et (4). On peut voir qu'il n'y a pas de différence marquée entre le courant PISHE normalisé collecté le long des directions cristallines [110] et [100].

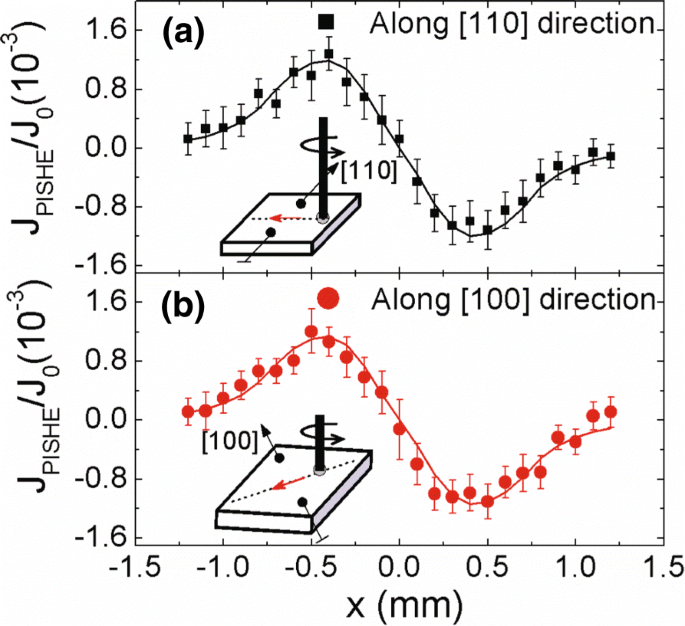
Le courant PISHE normalisé collecté le long de différentes orientations cristallines. Le courant PISHE est normalisé par le photocourant sous une polarisation de 0,3 V. Les symboles pleins sont les données expérimentales, et les traits pleins sont les résultats d'ajustement théoriques. Les encarts montrent les diagrammes schématiques des géométries de mesure correspondantes

Pour le mécanisme intrinsèque, le courant PISHE le long d'une certaine direction cristalline est lié à la division du spin dans cette direction. Pour connaître le dédoublement de spin d'anisotropie dans le GaAs/AlGaAs 2DEG, nous mesurons la dépendance à l'orientation cristalline du courant CPGE à température ambiante, c'est-à-dire que nous mesurons le courant CPGE lorsque les deux contacts sont le long [110] (ou [100 ]) direction and the incident plane of light lies in [1\(\bar {1}\)0] (or [010]) direction, of which the measurement results are shown by squares (or by circles) in Fig. 6 . It is worth mentioning that when measuring the CPGE current, the light spot is located at the midpoint of the connection of the two contacts, where the PISHE is zero according to [20]. The CPGE current is also normalized by the corresponding photocurrent under a bias of 0.3 V to eliminate the influence of the carrier mobility and the carrier density in different crystal directions [51]. Then, we use the following equation to fit the normalized angle-dependent CPGE current to obtain the relative SOC strength along different crystal directions [21, 27]:

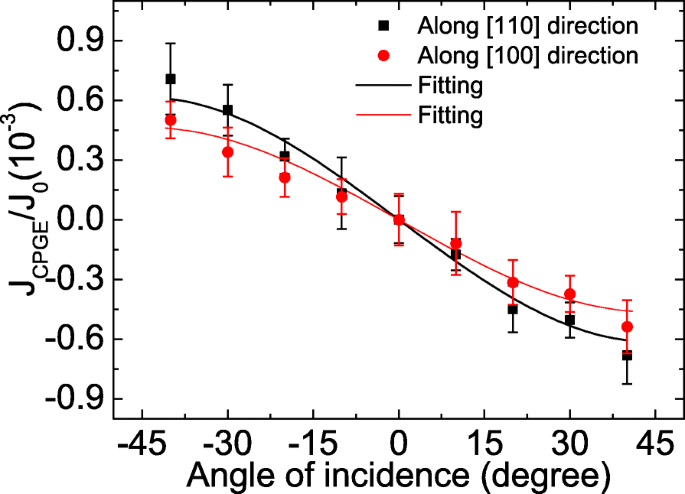
Incident angle dependence of the normalized CPGE current collected along different crystal orientations. The CPGE current is normalized by the photocurrent under a bias of 0.3 V. The solid symbols are the experimental data, and the lines are the fitting results according to Eq. (5)

Ici, θ is the angle of incidence, n is the refractive index of GaAs, and A _λ is a constant proportional to the SOC constant. The fitting results are shown by the solid lines in Fig. 6. When the incident plane of light lies in [1\(\bar {1}\)0] direction and the CPGE current is collected along [110] direction, the corresponding A parameter, denoted as A _[110] , is proportional to the sum of Rashba and Dresselhaus SOC, i.e., A _[110] ∝α +β [51–53]. When the incident plane of light lies in [010] direction and the CPGE current is collected along [100] direction, the corresponding A parameter, denoted as A _[100] , is proportional to the Rashba SOC, i.e., A _[100] ∝α [51–53]. Thus, by the ratio of A _[110] /Un _[100] , we can get the relative ratio of Rashba to Dresselhaus SOC, i.e., \(\beta /\alpha =\frac {A_{[110]}}{A_{[100]}}-1\) =0.32, which indicates that the spin splitting in the GaAs/AlGaAs 2DEG has crystal anisotropy [21]. Therefore, the intrinsic contribution to the PISHE should be sensitive to the crystal axis [16]. Specifically speaking, according to Eqs. (2) and (4), when the contacts are along [110] (or [100]) direction, the measured PISHE current is dominated by the inverse spin Hall current flowing nearly parallel to [110] (or [100]) direction since the PISHE current is a vortex current. If the intrinsic mechanism plays a dominant role in the 2DEG, the PISHE current collected along these two directions should be different. However, no marked difference is observed, which suggests that the extrinsic mechanism is dominant in the GaAs/AlGaAs 2DEG.

Conclusions

In conclusion, the PISHE current in a GaAs/AlGaAs 2DEG has been investigated in a temperature range of 77 to 300 K. The spin transverse force has been determined by fitting the PISHE current to a theoretical model. The dependence of the PISHE on the light power and on the light spot profiles has been investigated, which shows a good agreement with the theoretical model. The evolution of the PISHE current with temperature suggests that the PISHE is dominated by the extrinsic mechanism, which is further confirmed by the weak dependence of the PISHE current on the crystal orientation of the sample.

Abréviations

2DEG:

Two-dimensional electron gas

CPGE:

Circular photogalvanic effect

EMF:

Circular electromotive force

FWHM :

Pleine largeur à mi-hauteur

ISHE:

Inverse spin Hall effect

MBE :

Epitaxie par faisceau moléculaire

PISHE:

Photo-induced inverse spin Hall effect

ELLE :

Spin Hall effect

SOC:

Spin-orbit coupling