Impact des états de surface et de la fraction molaire d'aluminium sur le potentiel de surface et 2DEG dans les HEMT AlGaN/GaN
Résumé
La présence de pièges de surface est un phénomène important dans les HEMT AlGaN/GaN. Les propriétés électriques et physiques de ces pièges de surface ont été analysées à travers l'étude de la concentration d'électrons 2DEG ainsi que la variation du pourcentage d'aluminium dans la couche barrière de HEMT. Cette analyse montre que des donneurs profonds aux donneurs peu profonds, le changement en pourcentage de la densité électronique dans le 2DEG devient saturé (près de 8 %) avec le changement de la concentration en aluminium. La profondeur du potentiel quantique bien en dessous du niveau de Fermi est également analysée et s'avère saturée (près de 2%) avec le pourcentage d'aluminium lorsque l'énergie des états de surface du donneur passe de profonde à peu profonde. La physique derrière cet effet collectif est également analysée par le biais du diagramme de bande. L'effet des pièges donneurs de surface sur le potentiel de surface a également été discuté en détail. Ces états de surface sont modélisés comme des états donneurs. Donateur profond (E C − E D = 1.4 eV) au donneur peu profond (E C − E D = 0,2 eV) les pièges de surface sont minutieusement étudiés pour la concentration en donneurs de 10 11 à 10 16 cm −2 . Cette étude porte sur une variation de concentration en aluminium de 5 à 50 %. Cet article présente pour la première fois l'étude TCAD complète du donneur de surface et l'analyse de la concentration d'électrons dans le canal et la formation de 2DEG à l'interface AlGaN-GaN.
Introduction
Les applications haute fréquence et haute puissance sont les deux principales caractéristiques du matériau GaN qui ont été étudiées au cours des trois dernières décennies [1, 2]. L'un des principaux avantages de la structure AlGaN/GaN est la formation de 2DEG dans le puits de potentiel triangulaire à l'interface AlGaN-GaN même sans dopage intentionnel dans la couche barrière [3, 4]. Il est bien prouvé qu'il existe une polarisation spontanée et piézoélectrique dans la couche d'AlGaN de structure AlGaN/GaN [3]. Cette polarisation se traduit par deux nappes de charges opposées en bas et en haut de la couche barrière d'AlGaN. Ces charges de feuille de polarisation seules ne sont pas suffisantes pour former un puits de potentiel triangulaire à l'interface AlGaN-GaN. Afin de résoudre ce problème, Ibbetson et al. [5] ont suggéré qu'il devrait y avoir une feuille de charges positives qui doit exister à la surface de la couche d'AlGaN. Ces charges positives apparaissent en raison de l'ionisation des états donneurs de surface (1,42 eV de la bande de conduction avec 1,35 × 10 13 cm −2 ) en surface [6].
Vetury et al. [7] ont étudié l'effet de ces états de surface en utilisant des sondes potentielles comme grille flottante. L'effet des états de surface sur les performances DC et RF des HEMT AlGaN/GaN a été étudié [8, 9]. Le comportement de la porte de Schottky à l'échelle nanométrique discute de la formation de la porte virtuelle dans la région non fermée en raison des états donneurs de surface [10]. Les états donneurs de surface fixes sont utilisés pour analyser l'effet d'auto-échauffement dans HEMT [11]. Longobardi et al. [12] ont réalisé la première simulation TCAD pour étudier l'effet des états donneurs de surface sur les caractéristiques DC des MISFET AlGaN/GaN. Pour activer ces états donneurs de surface dans la simulation TCAD, Bakeroot et d'autres ont introduit un modèle différent [13, 14]. Les résistances drain/source dépendent également de la polarisation de la grille en raison de la formation de la grille virtuelle dans la région sans grille de la surface AlGaN. Pradeep et al. [15] ont développé la procédure d'extraction de la mobilité et de la résistance basée sur les caractéristiques DC de la région linéaire de l'AlGaN/GaN HEMT. Meneghesso et al. [16] ont discuté de l'état de surface comme d'un piège qui capture la couche de trous très dense à la surface d'AlGaN pour compenser les électrons dans 2DEG. Les pièges donneurs de surface disponibles au sommet de la couche d'AlGaN modifient le comportement électrique du dispositif lorsque ces pièges sont occupés par des électrons à polarisation de grille négative [17]. La relation entre les pièges donneurs de surface et les électrons 2DEG a également été discutée par simulation TCAD en adoptant des phénomènes de transport dépendant du temps [18]. Bien que différentes techniques de caractérisation aient été explorées, Tapajna et al. [19] ont utilisé la méthode des transitoires à seuil pour étudier les pièges accepteurs d'interface, mais la caractérisation des pièges donneurs de surface est encore inexplorée. Une approche de modélisation informatique extensive pour le piège de surface en tant que donneur a également été discutée [20]. Gucmann et al. [21] ont discuté du fait que si la densité du donneur de surface est supérieure à la concentration de charge de polarisation, alors l'électron est transféré à l'interface AlGaN-GaN pour générer le 2DEG dans le canal.
La littérature discutée ci-dessus a rapporté tant d'aspects pertinents de l'hétérostructure AlGaN/GaN mais ne tient pas compte de l'effet combiné du donneur de surface (Concentration + Énergie) et de la contribution de la concentration en aluminium dans la concentration électronique bidimensionnelle. Il est évident que le pourcentage d'aluminium est principalement responsable de la charge de polarisation dans la couche barrière d'AlGaN [3].
Pour fournir une compréhension physique appropriée d'un tel effet, nous avons couvert l'enquête suivante dans le présent travail (i) l'effet sur la concentration électronique bidimensionnelle avec des changements de piège de donneur de surface de profond à peu profond ainsi que des changements de pourcentage d'aluminium dans la couche barrière d'AlGaN, (ii) l'effet du piège de surface et du pourcentage d'aluminium sur le potentiel de surface et (iii) l'influence du piège donneur de surface et du pourcentage d'aluminium sur le puits de potentiel triangulaire à l'interface AlGaN-GaN.
Section de méthode et configuration de la simulation
Des simulations de dispositifs 2D ont été réalisées à l'aide de la version L-2016.12 de Sentaurus TCAD de Synopsys [22]. Nous avons calibré la configuration de la simulation TCAD en reproduisant le résultat expérimental de l'hétérostructure HEMT AlGaN/GaN [15], comme le montre la figure 1b.
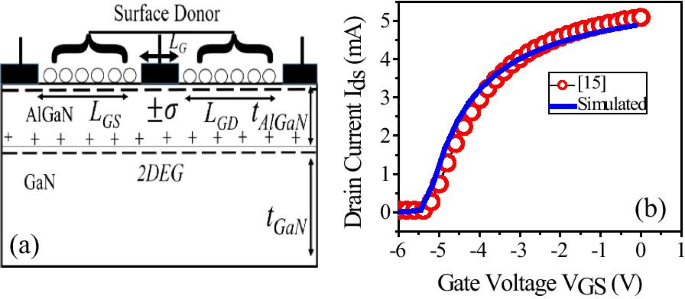
un Schéma d'une structure simulée en 2D avec une fraction molaire d'Al de 28 %. b Calibrage du montage de simulation en reproduisant les résultats expérimentaux rapportés [15]
L'appareil calibré a une couche barrière d'AlGaN de 30 nm au-dessus de la couche tampon de GaN de 2 μm. Longueur du portail Schottky (L G ) de 1 μm est placé symétriquement au sommet de la couche barrière d'AlGaN. Région non fermée de la porte au drain/source (L GD /L GS ) a une dimension de 2,5 μm chacun et la largeur de l'appareil est de 150 μm.
La plate-forme de simulation s'attaque à trois conditions (condition de Poisson et condition de continuité des électrons et des trous) qui supervisent le comportement du semi-conducteur.
Le modèle de transport de dérive et diffusion (DD) auto-cohérent est également inclus. La mobilité Lombardi et le modèle de mobilité unifié Philip ont été invoqués pour faciliter la dégradation de la mobilité due au champ électrique et au dopage. De plus, le modèle de recombinaison Auger et SRH (Shockley-Read-Hall) a été utilisé avec les statistiques de Fermi-Dirac. Le modèle Slotboom est activé pour rencontrer le rétrécissement de la bande interdite du drain fortement dopé et de la zone étendue de la source. Puisque cette structure a deux couches et que nous modifions le pourcentage d'aluminium dans la couche barrière d'AlGaN, la charge de polarisation est introduite selon l'équation de [3] :
$$\reste| {\sigma (x)} \right| =\gauche| {2\frac{a(0) - a(x)}{{a(x)}}\gauche\{ {e_{31} (x) - e_{33} \frac{{C_{13} (x )}}{{C_{33} (x)}}} \right\} + P_{{{\text{SP}}}} (x) - P_{{{\text{SP}}}} (0 )} \droit|$$ (1)où P SP est la polarisation spontanée, e 33 et e 31 sont des coefficients piézoélectriques, C 33 et C 31 sont des constantes élastiques, a est la constante de réseau et x est un pourcentage molaire d'aluminium.
La variation de la charge de polarisation ± σ AlGaN (x ) avec un pourcentage d'aluminium est illustré à la Fig. 2a [3]. Une fois la charge de polarisation calculée, l'équation de Poisson peut être résolue. À l'interface AlGaN-GaN, la bande de conduction change brusquement et forme un puits quantique de potentiel triangulaire étroit (1 à 4 nm) où les électrons s'accumulent. Comme ce potentiel quantique bien très étroit, la densité réduite des états devient dominante. L'équation quantique de Schrödinger explique bien le potentiel quantique mais est difficile à résoudre pour un dispositif HEMT plus grand. Pour capturer le comportement du puits de potentiel quantique, nous avons invoqué le modèle eQuantumpotential dans le Sentaurus TCAD qui active le modèle de correction quantique à gradient de densité [23] et donne un résultat proche de l'équation quantique de Schrodinger pour les appareils HEMT plus grands (dispositifs HEMT de puissance). Le modèle quantique à gradient de densité réduit la valeur maximale de la densité électronique dans 2DEG, et la valeur maximale s'éloigne également de l'interface AlGaN-GaN. Par conséquent, cela réduit le mécanisme de diffusion de l'interface et améliore la mobilité dans le canal, voir Fig. 2b [20]. Le modèle quantique à gradient de densité introduit un terme supplémentaire dans la formule de densité normale comme :
$$n =N_{{\text{C}}} F_{1/2} \left( {(E_{{\text{F}}} - E_{{\text{C}}} - \Lambda ) /kT} \right)$$ (2)où N C est la densité effective d'états, F 1/ 2 est une intégrale de Fermi d'ordre 1/ 2, E F est l'énergie quasi-Fermi pour les électrons, E C est le bord de la bande de conduction et kT représente l'énergie thermique des électrons. est calculé par :
$$\Lambda =- \left( {\left( {{{\gamma \hbar^{2} } \mathord{\left/ {\vphantom {{\gamma \hbar^{2} } {6m_{n} }}} \right. \kern-\nulldelimiterspace} {6m_{n} }}} \right) \cdot \left( {\nabla^{2} \sqrt n } \right)/\sqrt n } \right) $$ (3)où ħ = h /2π , h est une planche constante, m n est une masse effective de l'électron, γ (γ = 1.28) est un paramètre d'ajustement et n est la densité électronique.
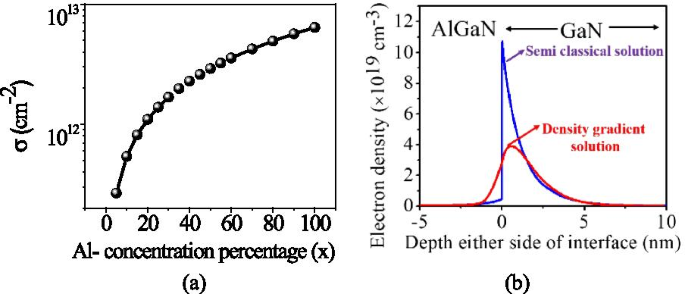
un Variation de la charge de la feuille de polarisation par rapport à la concentration en aluminium dans la couche barrière d'AlGaN [3]. b Effet de la captivité quantique sur la densité électronique 2DEG
Les pièges de surface ont été introduits comme état donneur (+ σ D ) à la surface des couches barrières d'AlGaN Fig. 1a, et la simulation a été réalisée à la température de 300 K. L'étalonnage a été effectué avec la concentration initiale en aluminium de 28 %.
Résultats de la simulation et discussion
Effet du pourcentage d'aluminium et des pièges de surface sur la densité 2DEG
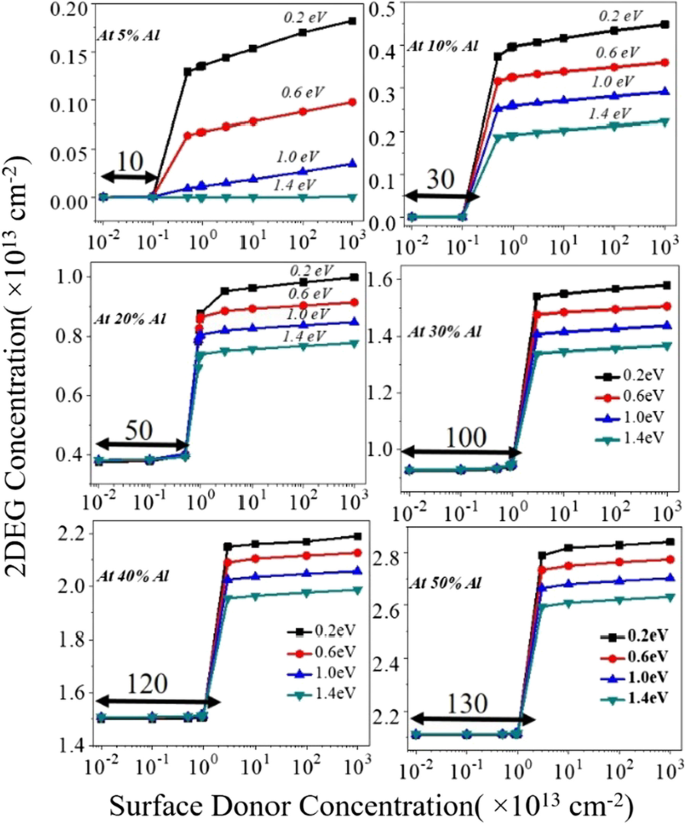
Le dispositif a été simulé dans des conditions de polarisation non appliquées pour étudier la densité électronique 2DEG. Alors que nous nous concentrons sur la densité électronique 2DEG, pour toute l'énergie de l'état du donneur, jusqu'à une certaine valeur (valeur relativement inférieure) de la concentration du piège donneur, il n'y a pas de changement significatif dans la densité électronique (c'est-à-dire, Région1). La densité électronique 2DEG change proportionnellement avec la concentration du donneur de surface (entre la région 1 et la région 2). Après une certaine valeur seuil du piège donneur de surface, encore une fois, aucun changement n'apparaît dans la densité électronique (c'est-à-dire la région 2), voir Fig. 3a–d. Ce mécanisme peut être expliqué comme suit :
un –d Variation de la densité de feuille d'électrons en 2DEG par rapport à la concentration et à l'énergie du donneur de surface (de 0,2 eV peu profond à 1,4 eV profond) pour différents pourcentages d'aluminium. e Distribution de charge différente et orientation du champ électrique dans l'appareil
(i) La bande de conduction de la couche barrière d'AlGaN pour la région 1 a un écart plus important par rapport au niveau de Fermi à la surface. Au fur et à mesure que la concentration du piège donneur commence à augmenter d'une valeur inférieure à une valeur supérieure, pendant la période de transition (entre la région 1 à la région 2), la bande de conduction commence proportionnellement à se déplacer vers le niveau de Fermi. Ainsi, la concentration de 2DEG commence à augmenter d'une valeur inférieure à une valeur supérieure. Au cours de la période de transition (entre la région 1 à la région 2), la bande de conduction commence proportionnellement à se déplacer vers le niveau de Fermi et donc l'énergie de surface du donneur se déplace également vers le niveau de Fermi. Pour la Région2, une fois que la concentration des donneurs dépasse la valeur seuil, la flexion de la bande de conduction commence de telle sorte que l'énergie du piège des donneurs épingle le niveau de Fermi. En raison du niveau de Fermi, tous les états donneurs sont ionisés et fournissent des électrons au potentiel quantique triangulaire 2DEG. Une fois que l'énergie des états donneurs est fixée au niveau de Fermi, aucun changement significatif ne se reflète dans la densité électronique. (ii) Pour trouver la neutralité de charge dans le dispositif, les états donneurs de surface sont essentiels pour contrer les électrons dans 2DEG. À mesure que les états donneurs de surface augmentent, un champ électrique commence à augmenter de la surface au puits quantique 2DEG. Ce champ électrique contrecarre le champ électrique intégré produit par la charge de feuille de polarisation (± σ AlGaN ). Lorsque le champ électrique externe commence à dépasser le champ électrique interne (en raison de ± σ AlGaN ), il fait baisser la bande de conduction à la surface et contribue donc plus d'électrons au puits de potentiel 2DEG, voir Fig. 3e. Lorsque le pourcentage d'aluminium augmente de 5 à 50 %, la densité de charge de la feuille de polarisation augmente également proportionnellement, ce qui conduit à un champ électrique interne élevé (en raison de la polarisation). Pour surmonter ce champ électrique interne, une concentration plus élevée de pièges donneurs de surface est nécessaire. Par conséquent, la région de transition est décalée (de 10 à 130 fois avec 10 11 cm −2 ) pour la valeur la plus élevée de la concentration du piège donneur, où la densité électronique 2DEG change proportionnellement à la concentration du piège donneur, Fig. 3a–d. La concentration de 2 DEG pour chaque pourcentage d'aluminium par rapport au donneur de surface (concentré + énergie) est tracée sur la Fig. 4. Malgré le modèle de concentration d'électrons de 2 DEG est le même pour tous les pourcentages d'aluminium lorsque le piège du donneur va de peu profond (0,2 eV) à profond (1,4 eV) (Fig. 5), le changement de densité électronique 2DEG de profond à peu profond est encore assez important. Dans le cas d'une concentration en aluminium de 5%, le piège donneur va de profond (1,4 eV) à peu profond (0,2 eV), il ne contribue pas de manière significative au puits de potentiel. Comme concentration de charge de polarisation (± σ ) est de l'ordre de 10 11 cm −2 pour 5 % d'aluminium, voir Fig. 2a, le champ électrique dû à ces charges de polarisation n'est pas suffisant pour amener le décalage de la bande de conduction en dessous du niveau de Fermi, par conséquent, aucun puits de potentiel triangulaire 2DEG n'est formé du côté GaN de la structure d'interface AlGaN-GaN. Il est également évident que même pour la concentration plus élevée de pièges donneurs de surface, la saturation de la densité électronique ne se produit pas comme le montrent les Fig. 4a et 6. Ceci est également vrai pour un pourcentage d'aluminium de 10 %, comme le montre la figure 4b. Pour 20% et au-delà, la concentration de charge de polarisation (± σ) est supérieure à 10 12 cm −2 . Ainsi, le champ électrique interne est suffisamment grand pour tirer le décalage de la bande de conduction en dessous du niveau de Fermi et, par conséquent, il forme le puits de potentiel quantique triangulaire 2DEG, voir Fig. 6b, c. Ainsi, pour un pourcentage d'aluminium de 20 % et plus, la densité électronique de 2 DEG approche de ~ 10 13 cm −2 pour les pièges à donneurs peu profonds, comme illustré à la Fig. 4c. Pour une concentration en aluminium de 20 %, 30 % et au-delà, la contribution de l'électron dans le puits triangulaire a une densité de 1 × 10 13 à 3 × 10 13 cm −2 . La figure 5a,b représente le pourcentage de variation de la densité électronique dans un puits triangulaire lorsque l'énergie du piège du donneur passe de 1,4e à 0,2 eV. Au fur et à mesure que nous passons de 5 à 50% de pourcentage d'aluminium, le changement de concentration en 2DEG diminue considérablement de 10,89 fois à 1,08 fois et devient saturé au-delà de 30%.
Variation d'un pourcentage d'aluminium individuel au piège de surface du donneur de profond à peu profond par rapport à la bande de conduction

un Changement de pourcentage à l'échelle logarithmique de la densité électronique 2DEG pour la concentration en Al lorsque le donneur de surface devient peu profond à partir du niveau profond par rapport à la bande de conduction. b Échelle linéaire
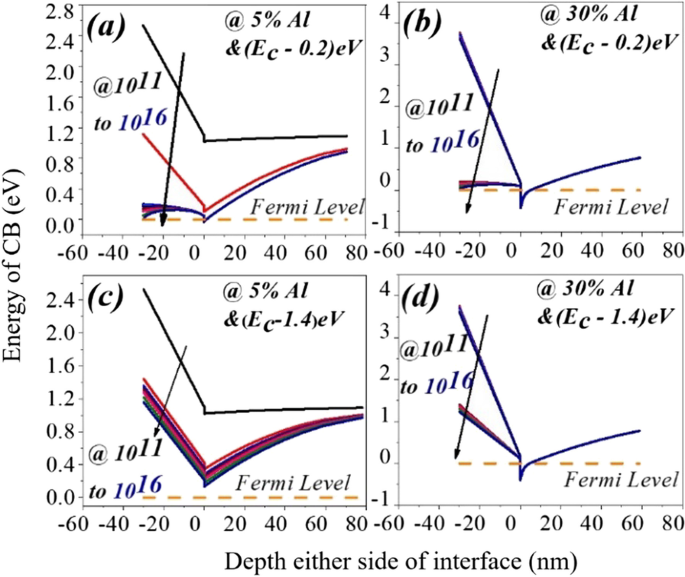
un , c Variation de la bande de conduction de part et d'autre de l'interface AlGaN–GaN pour 5 % d'aluminium et b , d pour 30% d'aluminium. Le piège de surface de niveau profond ne contribue pas à la charge d'électrons et de feuille positive au puits de potentiel et à la surface, ce qui augmente la pente de la bande de conduction. Même pour l'état de surface du donneur profond (1,4 eV), un puits de potentiel de 2 DEG se forme pour 30 % d'aluminium. Ce n'est pas vrai pour 5% d'aluminium
Effet du pourcentage d'aluminium et du piège de surface sur le potentiel de surface
Certaines publications ont discuté de la variation du potentiel de surface due au changement du pourcentage d'aluminium [29]. Mais ils n'ont pas intégré l'effet des pièges donneurs de surface sur le potentiel de surface. Nous rapportons ici la variation du potentiel de surface due aux pièges des donneurs de surface, à la fois dans les dimensions de l'énergie et de la concentration, voir Fig. 7a. Dans cette étude, nous avons changé la concentration du donneur de surface de 1 × 10 12 à 1 × 10 16 et l'énergie du donneur de surface de 0,2 à 1,4 eV. Le potentiel de surface a été calculé à partir de la figure 6b. Le potentiel de surface s'établit à près de 3,7 eV (pour une concentration de donneur de surface de 1 × 10 12 ) et 3,6 eV (pour une concentration de donneur de surface 1 × 10 13 ). Ce potentiel de surface ne dépend pas de l'énergie du piège donneur de surface pour sa valeur inférieure. Le potentiel de surface augmente linéairement à mesure que le donneur de surface va en profondeur (1,4 eV) depuis peu profond (0,2 eV). Au fur et à mesure que le potentiel de surface diminue, la concentration d'électrons 2DEG augmentera car le potentiel de surface varie linéairement avec l'énergie du piège du donneur de surface. Le pourcentage d'aluminium a également un impact important sur le potentiel de surface. En augmentant le pourcentage d'aluminium de 5 à 50 %, la concentration en électrons augmente de 7,79 × 10 11 à 2,75 × 10 13 . Le potentiel de surface augmente également de 0,49 à 0,576 eV lorsque le pourcentage d'aluminium passe de 5 à 50 %, voir Fig. 7b. Ainsi, la concentration et l'énergie du piège donneur de surface ainsi que la concentration d'aluminium ont une grande influence sur le potentiel de surface.
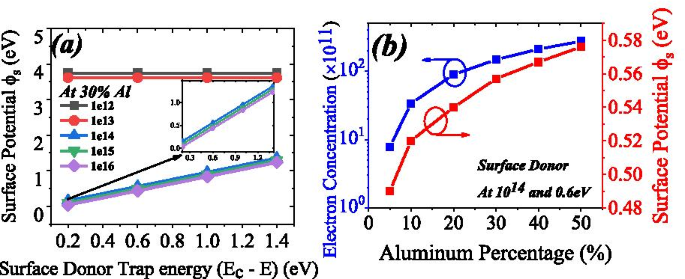
un Variation du potentiel de surface par rapport à l'énergie du piège donneur de surface. À une concentration plus faible (inférieure à 1e14), il n'y a pas de changement significatif du potentiel de surface. Concentration du donneur de surface supérieure à 1e13, le potentiel de surface change proportionnellement à l'énergie du donneur de surface. b Concentration électronique en 2DEG passant de 7.79 × 10 11 à 2,75 × 10 13 pour l'aluminium, le pourcentage passe de 5 % à 50 % (ligne bleue). Le potentiel de surface change d'environ 0,1 eV de 5 à 50 % du pourcentage d'aluminium
Effet du pourcentage d'aluminium et du piège de surface sur la bande de conduction et le puits de potentiel 2DEG
Les pièges de surface ionisés apportent des électrons au puits de potentiel et une charge de feuille positive à la surface d'AlGaN [6]. Dans le cas d'une concentration en aluminium de 5%, à mesure que les pièges vont en profondeur à partir d'un niveau d'énergie peu profond, la quantité de pièges de surface ionisés devient de plus en plus petite. Ainsi, les pièges de surface ionisés ont contribué moins d'électrons au puits de potentiel triangulaire et aux charges de feuille positives à la surface. Une quantité moindre de charges de feuille positives et de concentration d'électrons dans 2DEG ne contribue pas suffisamment au champ électrique externe et, par conséquent, la pente de la bande de conduction dans la couche d'AlGaN devient plus grande, comme le montre la figure 6. Ceci est également vrai pour l'aluminium avec 10 % dans la couche barrière d'AlGaN. Les électrons libres des états donneurs de surface résident dans un puits de potentiel 2DEG et neutralisent la charge de feuille positive qui apparaît à la surface d'AlGaN. Cette charge de feuille d'électrons est calculée par [24] :
$$n_{{\text{s}}} (x) =\frac{ + \sigma (x)}{e} - \left( {\frac{{\varepsilon_{o} \varepsilon (x)}} {{de^{2} }}} \right)\left[ {e\phi_{{\text{b}}} (x) + E_{{\text{F}}} - \Delta E_{{\ texte{C}}} (x)} \right]$$ (4)où d est l'épaisseur de l'Alx Ga(1−x ) N couche barrière, ϕ b est la barrière Schottky, E F est le niveau de Fermi et ΔE C est le décalage de la bande de conduction à l'interface AlGaN-GaN. Il est évident d'après l'Éq. (4) que la densité de charge de feuille d'électrons est directement proportionnelle au décalage de bande de conduction et aux charges de polarisation qui sont fonction du pourcentage d'aluminium. À mesure que nous augmentons le pourcentage d'aluminium de 10 à 50%, le décalage de la bande de conduction augmente [25] et donc la densité électronique dans 2DEG augmente en raison de l'augmentation du nombre de niveaux d'énergie, voir Fig. 8. Le champ électrique interne de l'appareil, lorsque la concentration en aluminium est de 20 % et plus, est telle que la pente de la bande de conduction est suffisamment élevée pour construire le puits de potentiel triangulaire, même pour une énergie de piège de surface de niveau profond (1,4 eV) et une concentration de piège de donneur de surface inférieure, comme indiqué sur la Fig. 6b, d .
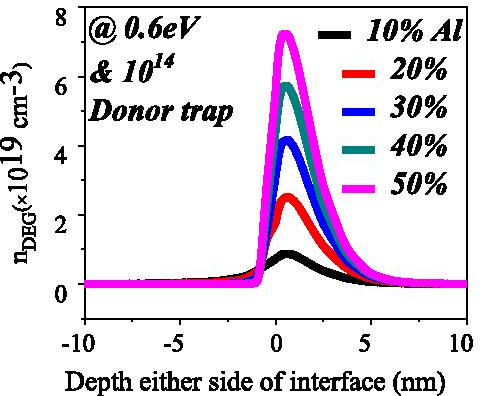
Densité électronique dans un puits de potentiel quantique triangulaire pour différentes concentrations d'aluminium à une concentration et une énergie de donneur fixes
Il est important de regarder l'encoche du potentiel quantique triangulaire bien formée en dessous du niveau de Fermi ((E F − E) eV), où E est l'énergie en dessous du niveau de Fermi. Deux paramètres importants dans le puits de potentiel quantique triangulaire sont la profondeur de potentiel bien en dessous du niveau de Fermi et la largeur du puits de potentiel au niveau de Fermi. Le confinement des électrons dans des régions à deux dimensions est appelé feuillet quantique 2DEG. La densité d'états N (E ) est l'une des caractéristiques importantes du puits de potentiel quantique 2DEG. La densité d'états dans un puits quantique bidimensionnel est définie comme [26] :
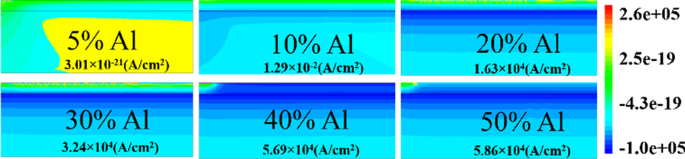
$$N(E) =\left( {{{m^{*} L_{{\text{X}}}^{2} E} \mathord{\left/ {\vphantom {{m^{*} L_{{\text{X}}}^{2} E} {\pi \hbar^{2} }}} \right. \kern-\nulldelimiterspace} {\pi \hbar^{2} }}} \ à droite)$$ (5)où m** est la masse effective de l'électron et L X est la largeur du puits. Cette densité d'état dans un puits bidimensionnel ressemble à une fonction échelonnée.
Le nombre d'états occupés dépend du niveau de Fermi. Par exemple, si le niveau de Fermi est supérieur à E 1 mais moins de E 2; alors seulement E 1 la sous-bande est remplie. Si le niveau de Fermi est supérieur à E 2 , mais inférieur à E 3 , puis deux sous-bandes inférieures E 2 et E 1 sont remplis d'électrons comme le montre la figure 9b. Cela signifie que si l'énergie à l'interface va plus loin avec le niveau de Fermi, alors seuls des électrons seront attendus en grand nombre. Dans l'hétérostructure AlGaN/GaN l'espacement énergétique diminue ((E 2 − E 1 ) > (E 3 − E 2 )) pour les sous-bandes supérieures [27]. À mesure que l'énergie des sous-bandes augmente, la différence entre elles devient négligeable et semble continue. La solution rigoureusement correcte de la fonction d'onde contient simultanément l'équation de Poisson et l'équation de Schrödinger. Mais le modèle de gradient de densité génère le résultat approximatif égal avec l'équation de Schrödinger. Dans le puits de potentiel quantique, le niveau d'énergie est quantifié car ce puits se forme jusqu'à quelques nm de longueur du côté GaN de l'interface AlGaN-GaN. L'encoche la plus profonde en dessous du niveau de Fermi aura certainement un nombre plus élevé de niveaux d'énergie quantifiés. Le niveau d'énergie quantifié en dessous du niveau de Fermi est occupé. Par conséquent, plus l'énergie est profonde en dessous du niveau de Fermi, la concentration en électrons sera plus élevée en 2DEG. D'après la figure 9a, il est clair que le niveau d'énergie en dessous du niveau de Fermi augmente lorsque le pourcentage d'aluminium augmente, car la charge de polarisation augmente et donc le champ électrique interne rend l'encoche plus profonde. En ce qui concerne l'énergie des donneurs de surface, il ressort de la discussion précédente que lorsque les pièges de surface s'enfoncent plus profondément (1,4 eV), l'ionisation de ces donneurs de surface diminue. Par conséquent, le champ électrique est généré en raison de charges de feuille positives à la surface et les électrons apportés par ces donneurs de surface à 2DEG ne sont pas suffisants pour surmonter le champ électrique interne. Ainsi, l'effet de la charge de polarisation en termes de champ électrique diminue, ce qui conduit à des niveaux d'énergie inférieurs au niveau de Fermi. Une exception est pour la concentration d'aluminium de 5 %, il ressort clairement de la figure 10a que la valeur de E F − E est négatif car le niveau de Fermi est supposé au niveau zéro, pour les pièges donneurs profonds (> 0,9 eV à 1,4 eV), ce qui signifie que l'énergie E est supérieur au niveau de Fermi (2DEG ne se forme pas). Pour les pièges donneurs à surface moins profonde (< 0,9 eV à 0,2 eV), la valeur de E F − E est positif, ce qui signifie que la valeur du E est inférieur au niveau de Fermi. Pour le reste de la concentration en aluminium (10 % à 50 %), la valeur de E F − E est positif ce qui signifie que la valeur de E est inférieur au niveau de Fermi et une encoche de 2DEG se forme pour tous les types d'énergie du donneur de surface (de 0,2 eV à 1,4 eV). Il est noté à partir de la Fig. 11a que la variation en pourcentage de l'énergie E avec de l'aluminium est saturé au-delà de la concentration en aluminium de 20 %, ce qui est également en accord avec la figure 5. La profondeur de l'entaille en dessous du niveau de Fermi ne change pas de manière significative après une concentration en aluminium de 20 % lorsque le donneur de surface piège l'énergie de profond à peu profond. La figure 11b montre également qu'il n'y a pas de courant significatif jusqu'à 10 % de fraction molaire d'aluminium. Au-delà de 10 %, il y a un changement significatif dans le courant lorsque l'énergie du donneur de surface change de E C − 0.2 à E C − 1.4 eV et à nouveau saturé au-delà de 20 %. Ce résultat est également en accord avec les Figs. 11a et 5. Le tracé de contour de la densité de courant absolue montre également qu'il sature au-dessus de 20 % de fraction molaire d'Al et aucune densité de courant significative jusqu'à 10 % de la fraction molaire d'Al. Fig. 12. Cela valide également la non-formation de 2DEG jusqu'à 10 % d'Al fraction molaire. Une quantité importante de densité électronique observée au-dessus de 20% de la fraction molaire Fig. 13a. La distribution du champ électrique le long du canal est tracée sur la figure 13b. La figure 13b montre qu'il n'y a pas de champ électrique considérablement amélioré sous la grille jusqu'à 10 % de la fraction molaire d'Al et au-dessus de 20 % de la fraction molaire d'Al, il n'y a pas beaucoup de différence de champ électrique, ce qui limite le courant à un pourcentage d'Al plus élevé.
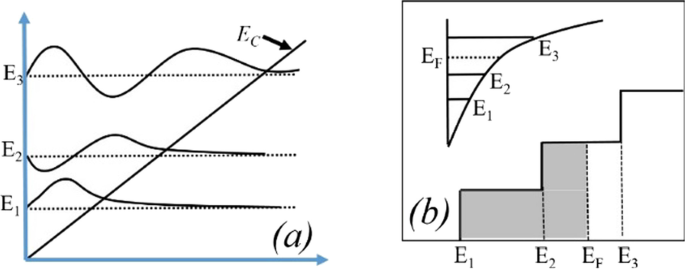
un Un potentiel triangulaire représentant bien les énergies des sous-bandes avec Fang-Howard Airy fonction d'onde. b Seules les sous-bandes d'énergie inférieure (E 1 et E 2 , inférieur au niveau de Fermi) sont occupés [28]
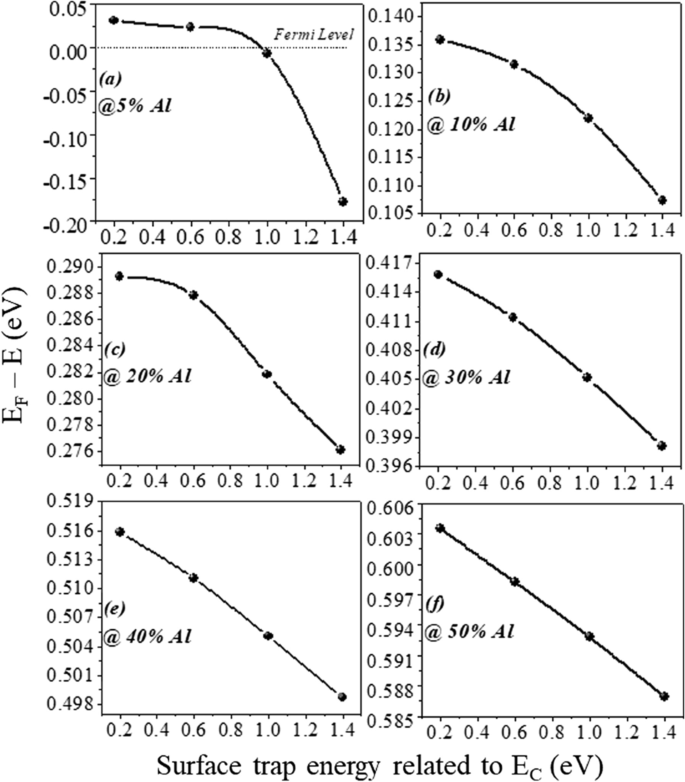
un –f (E F − E ) variation avec l'énergie du donneur de surface pour toutes les concentrations d'aluminium
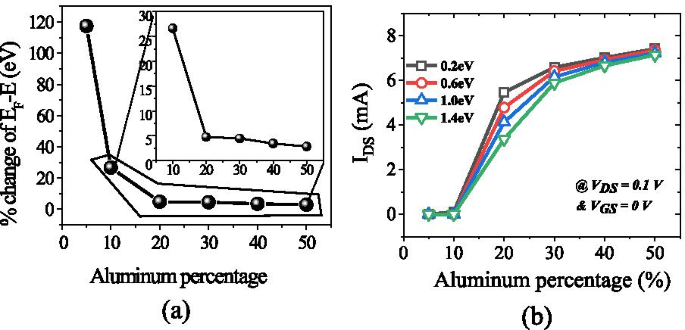
un La variation en pourcentage de l'énergie E avec la concentration d'aluminium lorsque l'énergie du donneur de surface passe de profond à peu profond. b Courant de vidange et V DS = 0.1 V et V GS = 0 V à différentes surfaces d'énergie des pièges des donneurs. Jusqu'à 10 % aucun courant significatif observé dans l'appareil

Tracé de contour de la densité de courant totale absolue pour une énergie de surface du donneur de 0,6 eV à V DS = 0.1 V et V GS = 0 V
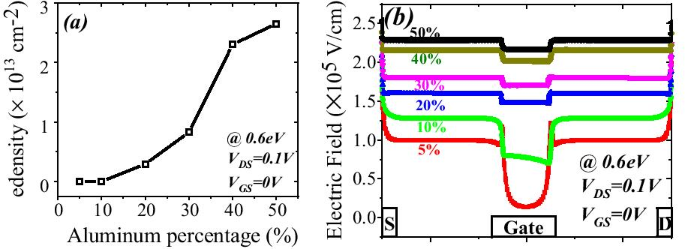
un Electron density variation with aluminum percentage and b electric field variation below gate and either side of gate for different aluminum percentage
Conclusion
In this paper, we comprehensively present the effect of surface donor traps along with aluminum percentage on electron density and quantum potential well. This manuscript demonstrated that the percentage change happens in 2DEG and notch below the Fermi level gets saturated above 20% of aluminum concentration when surface donor trap energy goes deep to shallow. The electron density in the two-dimensional quantum potential well is saturated approximately at 8%, whereas the energy below the Fermi level saturates somewhere around 2%. These two results are also in tune with each other, except 5% aluminum, having a condition for not forming two-dimensional well for relatively deep (> 0.9 eV) surface donors. Aluminum percentage above 10% forms two-dimensional quantum potential well even for deeper surface donor traps. The effect of surface donor traps on the surface potential also has been discussed in this work. The results of this paper may provide the impetus to the experimental result validation.
Availability of data and materials
All data are available on request.
Abréviations
- GaN:
-
Gallium nitride
- HEMT:
-
High-electron-mobility transistor
- 2DEG:
-
Two-dimensional electron gas
- DD:
-
Drift and diffusion transport model
- SRH:
-
Shockley–Read–Hall recombination model
Nanomatériaux
- Évaluer l'IoT et l'impact de la 5G
- 5G et GaN :futures innovations
- Réglage de la chimie de surface du polyétheréthercétone par revêtement d'or et traitement au plasma
- Étude sur la polarisation de surface de l'hétérostructure GaN/AlGaN/GaN coiffée d'Al2O3 par spectroscopie photoélectronique à rayons X à résolution angulaire
- Réglage des morphologies de surface et des propriétés des films de ZnO par la conception de la couche interfaciale
- Électrofilage sur des substrats isolants en contrôlant la mouillabilité et l'humidité de la surface
- Les effets de couplage des polaritons de plasmon de surface et des résonances dipolaires magnétiques dans les métamatériaux
- Propriétés et fonctions :bronze d'aluminium
- En savoir plus sur les différentes finitions de surface de PCB et leur impact sur votre PCB



