Théorème de Norton. Procédure facile étape par étape avec exemple

Théorème de Norton dans l'analyse des circuits CC

Le théorème de Norton est une autre technique utile pour analyser les circuits électriques, comme l'utilisation du théorème de Thevenin, qui réduit les circuits actifs linéaires et les réseaux complexes en un simple circuit équivalent. La principale différence entre le théorème de Thevenin et le théorème de Norton est que le théorème de Thevenin fournit une source de tension équivalente et une résistance série équivalente, tandis que le théorème de Norton fournit une source de courant équivalente et une résistance parallèle équivalente.

Théorème de Norton déclare que :

En d'autres termes, mais simples, tout circuit linéaire équivaut à une source de courant réelle et indépendante dans des bornes spécifiques.

Message connexe :Théorème de Thevenin. Procédure facile étape par étape avec exemple (vues illustrées)

Étapes pour analyser un circuit électrique à l'aide du théorème de Norton

1. Court-circuitez la résistance de charge.
2. Calculer/mesurer le courant de court-circuit. C'est le courant de Norton (I_N ).
3. Sources de courant ouvertes, sources de tension courtes et résistance de charge ouverte.
4. Calculer/mesurer la résistance en circuit ouvert. C'est la résistance de Norton (R_N ).
5. Maintenant, redessinez le circuit avec le courant de court-circuit mesuré (I_N ) à l'étape (2) en tant que source de courant et résistance de circuit ouvert mesurée (R_N ) à l'étape (4) en tant que résistance parallèle et connectez la résistance de charge que nous avions retirée à l'étape (3). C'est le circuit Norton équivalent de ce réseau électrique linéaire ou circuit complexe qui a dû être simplifié et analysé. Vous l'avez fait.
6. Trouvez maintenant le courant de charge traversant et la tension de charge à travers la résistance de charge en utilisant la règle du diviseur de courant. Je_L =I_N / (R_N / (R_N + R_L ))  ((Pour une explication claire... consultez l'exemple résolu ci-dessous).

Exemple résolu par Norton Théorème :

Exemple :

Rechercher R_N , je_N , le courant traversant et la tension de charge à travers la résistance de charge de la figure (1) en utilisant le théorème de Norton.

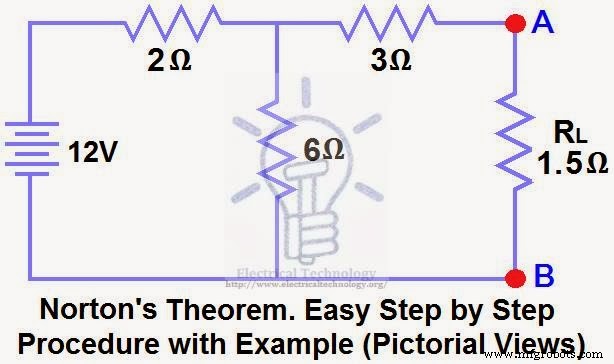
  Solution :-

ÉTAPE 1.

Court-circuitez la résistance de charge de 1,5 Ω comme indiqué sur la (Fig 2).

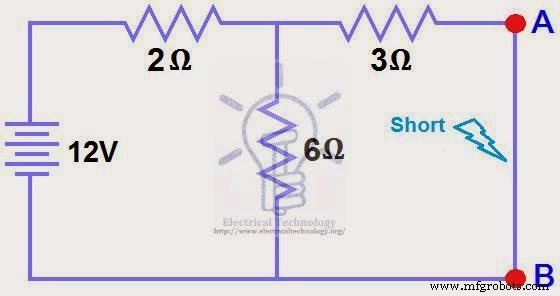
ÉTAPE 2.

Calculer/mesurer le courant de court-circuit. C'est le courant de Norton (I_N ).

Nous avons court-circuité les bornes AB pour déterminer le courant Norton, I_N. Les 6Ω et 3Ω sont alors en parallèle et cette combinaison parallèle de 6Ω et 3Ω est alors en série avec 2Ω.

Ainsi, la résistance totale du circuit à la Source est :-

2Ω + (6Ω || 3Ω) ….. (|| =en parallèle avec).

R_T =2Ω + [(3Ω x 6Ω) / (3Ω + 6Ω)] → I_T =2Ω + 2Ω =4Ω.

R_T =4Ω

I_T =V ÷ R_T

I_T =12V ÷ 4Ω

I_T =3A..

Nous devons maintenant trouver I_SC =I_N   … Appliquer CDR… (règle du diviseur actuel)…

Je_SC =I_N =3A x [(6Ω ÷ (3Ω + 6Ω)] =2A.

I_SC =Je_N =2A.

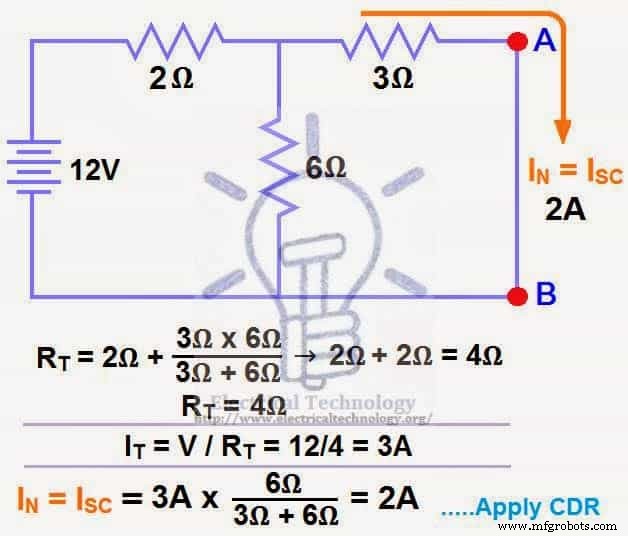
ÉTAPE 3.

Sources de courant ouvertes, sources de tension courtes et résistance de charge ouverte. Image (4)

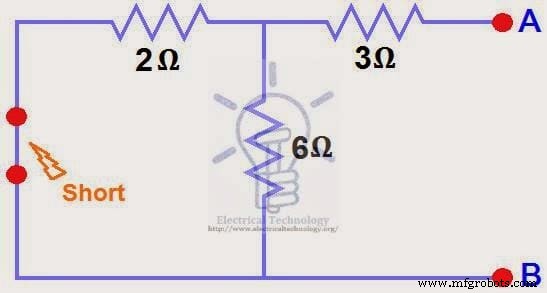
ÉTAPE 4.

Calculer/mesurer la résistance en circuit ouvert. C'est la résistance de Norton (R_N )

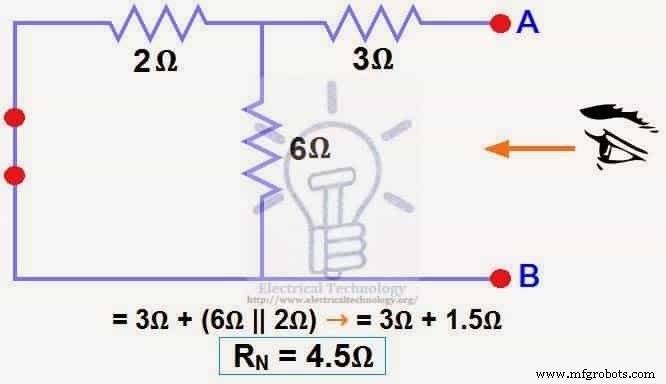
Nous avons réduit la source 12 V CC à zéro équivaut à la remplacer par un court-circuit à l'étape (3), comme illustré à la figure (4). Nous pouvons voir que la résistance de 3 Ω est en série avec une combinaison parallèle de résistance 6Ω et résistance 2Ω. c'est-à-dire :

3Ω + (6Ω || 2Ω) ….. (|| =en parallèle avec)

R_N =3Ω + [(6Ω x 2Ω) ÷ (6Ω + 2Ω)]

R_N =3Ω + 1.5Ω

R_N =4.5Ω

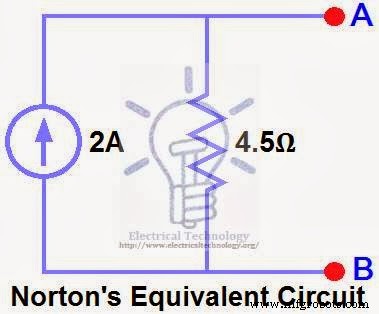
ÉTAPE 5.

Connectez le R_N en parallèle avec la source de courant I_N  et reconnectez la résistance de charge. Ceci est illustré à la figure (6), c'est-à-dire un circuit équivalent Norton avec résistance de charge.

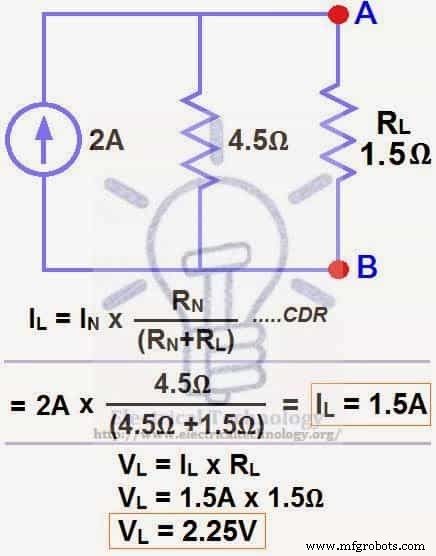
ÉTAPE 6.

Appliquez maintenant la dernière étape, c'est-à-dire calculez le courant de charge à travers et la tension de charge à travers la résistance de charge par la loi d'Ohm, comme indiqué sur la figure 7. 

Courant de charge à travers la résistance de charge…

I_L =I_N x [R_N ÷ (R_N + R_L )]

=2A x (4,5Ω ÷ 4,5Ω + 1,5Ω) → =1,5A

I_L =1. 5A

Et

Tension de charge sur la résistance de charge…

V_L =I_L x R_L

V_L =1,5A x 1,5Ω

V_L =2,25 V

Comparez maintenant ce circuit simple avec le circuit d'origine donné dans la figure 1. Pouvez-vous voir à quel point il sera plus facile de mesurer/calculer le courant de charge et la tension de charge pour différentes résistances de charge grâce au théorème de Norton, même dans des circuits beaucoup plus complexes ? Seulement et seulement oui.

Bon à savoir : Les théorèmes de Norton et de Thevenin peuvent être appliqués aux circuits AC et DC contenant des composants de différence tels que des résistances, des inductances et des condensateurs, etc. Gardez à l'esprit que le courant de Norton "I_N " dans le circuit AC est exprimé en nombre complexe (forme polaire) alors que la résistance de Norton "R_N ” est indiqué sous forme rectangulaire.

Messages associés :

• Théorème de transfert de puissance maximale pour les circuits AC et DC
• Loi du courant et de la tension de Kirchhoff (KCL et KVL) | Exemple résolu
• Théorème de compensation :preuve, explication et exemples résolus
• Théorème de substitution – Guide étape par étape avec exemple résolu
• Théorème de Millman – Analyse des circuits CA et CC – Exemples
• Théorème de superposition – Analyse de circuit avec exemple résolu
• Théorème de Tellegen – Exemples résolus et simulation MATLAB
• Analyse de circuit SUPERNODE | Pas à pas avec un exemple résolu
• Analyse de circuit SUPERMESH | Pas à pas avec un exemple résolu
• Règle du diviseur de tension (VDR) – Exemples résolus pour les circuits R, L et C
• Règle du diviseur de courant (CDR) – Exemples résolus pour les circuits CA et CC
• Conversion étoile à delta et delta à étoile. Transformation Y-Δ