Machines à états finis

Jusqu'à présent, chaque circuit présenté était une combinatoire circuit. Cela signifie que sa sortie ne dépend que de ses entrées de courant. Les entrées précédentes pour ce type de circuits n'ont aucun effet sur la sortie.

Cependant, il existe de nombreuses applications où il est nécessaire que nos circuits aient de la « mémoire »; pour se souvenir des entrées précédentes et calculer leurs sorties en fonction de celles-ci. Un circuit dont la sortie dépend non seulement de l'entrée actuelle mais aussi de l'historique de l'entrée est appelé un circuit séquentiel .

Dans cette section, nous apprendrons comment concevoir et construire de tels circuits séquentiels. Afin de voir comment fonctionne cette procédure, nous allons utiliser un exemple, sur lequel nous étudierons notre sujet.

Supposons donc que nous ayons un jeu de quiz numérique qui fonctionne sur une horloge et lit une entrée à partir d'un bouton manuel. Cependant, nous voulons que le commutateur ne transmette qu'une seule impulsion HAUTE au circuit. Si nous accrochons le bouton directement sur le circuit du jeu, il transmettra HIGH pendant aussi peu de cycles d'horloge que notre doigt peut le faire. Sur une fréquence d'horloge commune, notre doigt ne peut jamais être assez rapide.

La procédure de conception comporte des étapes spécifiques qui doivent être suivies afin d'effectuer le travail :

Étape 1

La première étape de la procédure de conception consiste à définir avec des mots simples mais clairs ce que nous voulons que notre circuit fasse :

« Notre mission est de concevoir un circuit secondaire qui transmettra une impulsion ÉLEVÉE d'une durée d'un seul cycle lorsque le bouton manuel est enfoncé, et ne transmettra pas d'autre impulsion tant que le bouton n'est pas enfoncé et enfoncé à nouveau. »

Étape 2

L'étape suivante consiste à concevoir un diagramme d'état.

Il s'agit d'un schéma composé de cercles et de flèches et décrivant visuellement le fonctionnement de notre circuit. En termes mathématiques, ce schéma qui décrit le fonctionnement de notre circuit séquentiel est une machine à états finis. Notez qu'il s'agit d'une machine à états finis de Moore.

Sa sortie est fonction uniquement de son état actuel, pas de son entrée. Cela contraste avec la machine à états finis Mealy, où l'entrée affecte la sortie. Dans ce didacticiel, seule la machine à états finis de Moore sera examinée.

Le diagramme d'état de notre circuit est le suivant :(Figure ci-dessous)

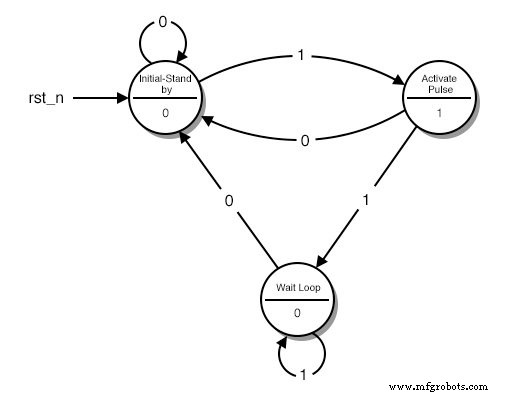
Un diagramme d'état

Chaque cercle représente un « état », une condition bien définie dans laquelle notre machine peut être trouvée. Dans la moitié supérieure du cercle, nous décrivons cette condition. La description nous aide à nous souvenir de ce que notre circuit est censé faire dans ces conditions.

• Le premier cercle est la condition « veille ». C'est de là que part notre circuit et qu'il attend une autre pression sur un bouton.
• Le deuxième cercle est la condition où le bouton vient d'être enfoncé et notre circuit doit transmettre une impulsion HAUTE.
• Le troisième cercle est la condition où notre circuit attend que le bouton soit relâché avant de revenir à la condition « veille ».

Dans la partie inférieure du cercle se trouve la sortie de notre circuit. Si nous voulons que notre circuit transmette un HAUT sur un état spécifique, nous mettons un 1 sur cet état. Sinon on met un 0.

Chaque flèche représente une « transition » d'un état à un autre. Une transition se produit une fois par cycle d'horloge. Selon l'entrée actuelle, nous pouvons passer à un état différent à chaque fois. Remarquez le nombre au milieu de chaque flèche. Il s'agit de l'entrée actuelle.

Par exemple, lorsque nous sommes dans l'état « Initial-Stand by » et que nous « lisons » un 1, le schéma nous indique qu'il faut passer à l'état « Activer Pulse ». Si nous lisons un 0, nous devons rester sur l'état "Initial-Stand by".

Alors, que fait exactement notre « Machine » ? Il part de l'état « Initial - Stand by » et attend jusqu'à ce qu'un 1 soit lu à l'entrée. Ensuite, il passe à l'état « Activer l'impulsion » et transmet une impulsion HAUTE sur sa sortie. Si le bouton continue d'être enfoncé, le circuit passe au troisième état, le « Wait Loop ».

Là, il attend que le bouton soit relâché (l'entrée passe à 0) tout en transmettant un LOW sur la sortie. Ensuite, c'est encore une fois !

C'est probablement la partie la plus difficile de la procédure de conception, car elle ne peut pas être décrite par des étapes simples. Il faut de l'expérience et un peu de réflexion pour mettre en place un diagramme d'état, mais le reste n'est qu'un ensemble d'étapes prédéterminées.

Étape 3

Ensuite, nous remplaçons les mots qui décrivent les différents états du diagramme par binaire Nombres. On démarre l'énumération à partir de 0 qui est affecté sur l'état initial. Nous continuons ensuite l'énumération avec n'importe quel état que nous aimons, jusqu'à ce que tous les états aient leur numéro. Le résultat ressemble à ceci :(Figure ci-dessous)

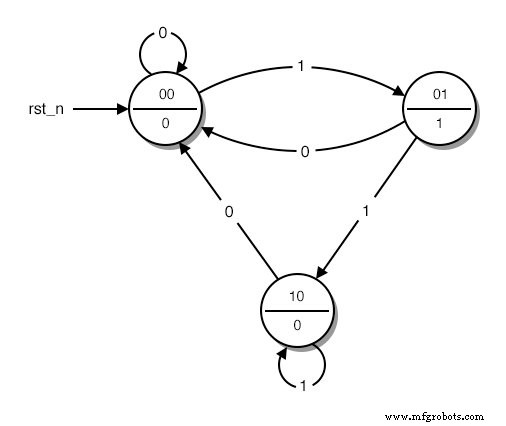
Un diagramme d'état avec des états codés

Étape 4

Ensuite, nous remplissons la Table d'état . Ce tableau a une forme très spécifique. Je vais donner le tableau de notre exemple et m'en servir pour expliquer comment le remplir. (Figure ci-dessous)

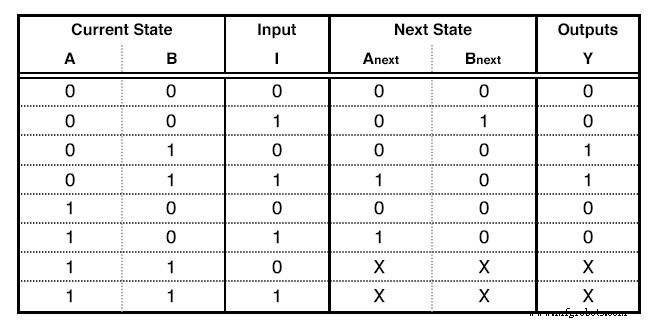
Une table d'état

Les premières colonnes sont autant de bits du nombre le plus élevé que nous avons attribué au diagramme d'état. Si nous avions eu 5 états, nous aurions utilisé jusqu'au nombre 100, ce qui signifie que nous aurions utilisé 3 colonnes. Pour notre exemple, nous avons utilisé jusqu'au nombre 10, donc seulement 2 colonnes seront nécessaires. Ces colonnes décrivent l'État actuel de notre circuit.

À droite des colonnes État actuel, nous écrivons les Colonnes d'entrée . Celles-ci seront autant que nos variables d'entrée. Notre exemple n'a qu'une seule entrée.

Ensuite, nous écrivons les colonnes d'état suivant . Ce sont autant que les colonnes État actuel.

Enfin, nous écrivons les Colonnes de sortie . Ceux-ci sont autant que nos sorties. Notre exemple n'a qu'une seule sortie. Puisque nous avons construit une machine à états plus finis, la sortie ne dépend que des états d'entrée actuels. C'est la raison pour laquelle la colonne des sorties a deux 1 :pour aboutir à une fonction booléenne de sortie indépendante de l'entrée I. Continuez à lire pour plus de détails. Les colonnes Current State et Input sont les Inputs de notre table. On les remplit avec tous les nombres binaires de 0 à :

2 ^{(Nombre de colonnes État actuel + Nombre de colonnes d'entrée)} -1

C'est plus simple qu'il n'y paraît heureusement. Habituellement, il y aura plus de lignes que les états réels que nous avons créés dans le diagramme d'état, mais ce n'est pas grave.

Chaque ligne des colonnes État suivant est remplie comme suit :Nous la remplissons avec l'état que nous atteignons lorsque, dans le diagramme d'état, à partir de l'état actuel de la même ligne, nous suivons l'entrée de la même ligne. Si vous devez remplir une ligne dont le numéro d'état actuel ne correspond à aucun état réel dans le diagramme d'état, nous le remplissons avec les termes Don't Care (X). Après tout, peu nous importe où nous pouvons aller depuis un État qui n'existe pas. Nous ne serions pas là en premier lieu! Encore une fois, c'est plus simple qu'il n'y paraît.

La colonne des sorties est remplie par la sortie de l'état actuel correspondant dans le diagramme d'état.

Le tableau d'état est complet ! Il décrit le comportement de notre circuit aussi complètement que le diagramme d'état.

Étape 5a

L'étape suivante consiste à prendre cette « Machine » théorique et à la mettre en œuvre dans un circuit. Le plus souvent, cette implémentation implique des tongs. Ce guide est dédié à ce type de mise en œuvre et décrira la procédure pour les deux D - Flip Flops ainsi que JK - Flip Flops. T - Les tongs ne seront pas incluses car elles sont trop similaires aux deux cas précédents. La sélection de la bascule à utiliser est arbitraire et est généralement déterminée par des facteurs de coût. Le meilleur choix est d'effectuer à la fois l'analyse et de décider quel type de Flip Flop entraîne un nombre minimum de portes logiques et un coût moindre.

Nous allons d'abord examiner comment nous implémentons notre « Machine » avec des D-Flip Flops.

Nous aurons besoin d'autant de D - Flip Flops que de colonnes State, 2 dans notre exemple. Pour chaque Flip Flop, nous ajouterons une colonne supplémentaire dans notre table State (Figure ci-dessous) avec le nom de l'entrée de la Flip Flop, "D" pour ce cas. La colonne qui correspond à chaque Flip Flop décrit quelle entrée nous devons donner à la Flip Flop pour passer de l'état actuel à l'état suivant . Pour le D - Flip Flop, c'est facile :l'entrée nécessaire est égale à l'état suivant. Dans les lignes qui contiennent des X, nous remplissons également des X dans cette colonne.

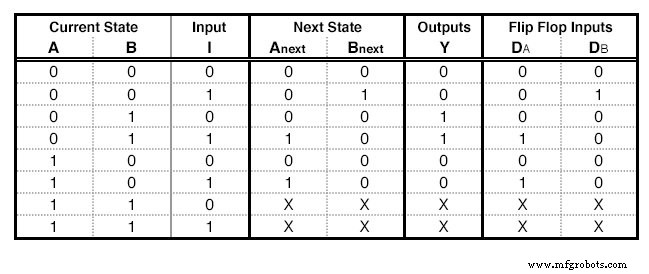
Une table d'état avec D - Excitations Flip Flop

Étape 5b

Nous pouvons faire les mêmes étapes avec JK - Flip Flops. Il existe cependant quelques différences. Un JK - Flip Flop a deux entrées, nous devons donc ajouter deux colonnes pour chaque Flip Flop. Le contenu de chaque cellule est dicté par la table d'excitation du JK :

Ce tableau dit que si on veut passer de l'état Q à l'état Q_suivant , nous devons utiliser l'entrée spécifique pour chaque terminal. Par exemple, pour passer de 0 à 1, nous devons alimenter J avec 1 et nous s'en fout quelle entrée nous alimentons au terminal K.

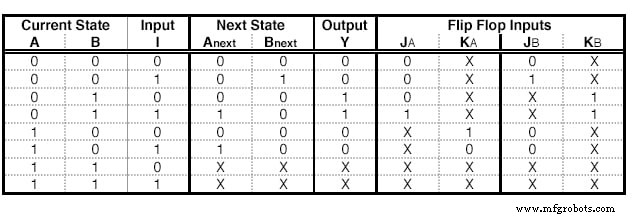
Une table d'état avec JK - Flip Flop Excitations

Étape 6

Nous sommes dans la phase finale de notre procédure. Reste à déterminer les fonctions booléennes qui produisent les entrées de nos tongs et la sortie. Nous extrairons une fonction booléenne pour chaque entrée Flip Flop que nous avons. Cela peut être fait avec une carte de Karnaugh. Les variables d'entrée de cette carte sont les variables d'état actuel ainsi que les entrées.

Cela dit, les fonctions d'entrée de nos D - Flip Flops sont les suivantes :(Figure ci-dessous)

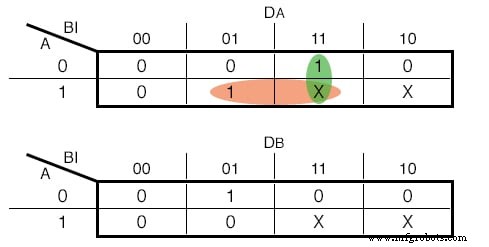
Cartes de Karnaugh pour les entrées D - Flip Flop

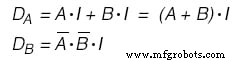
Si nous choisissions d'utiliser JK - Flip Flops, nos fonctions seraient les suivantes :(Figure ci-dessous)

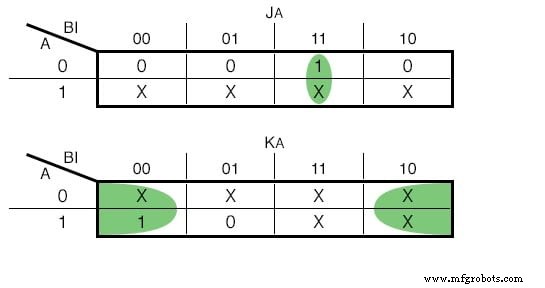
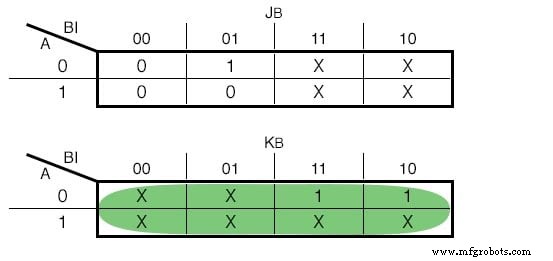
Carnaugh Map for the JK - Flip Flop Input

Une carte de Karnaugh sera également utilisée pour déterminer la fonction de la sortie :(Figure ci-dessous)

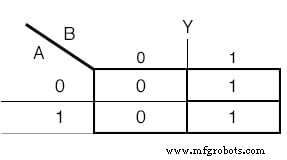
Carnaugh Map pour la variable de sortie Y

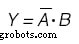
Étape 7

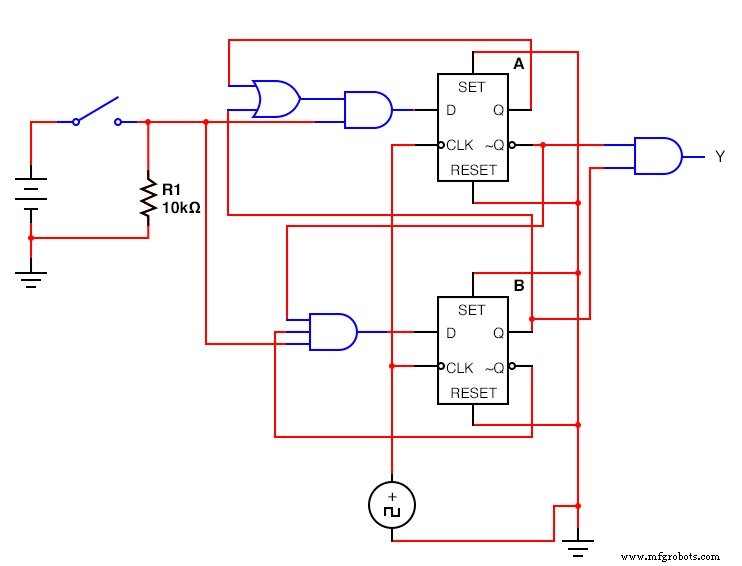
Nous concevons notre circuit. Nous plaçons les bascules et utilisons des portes logiques pour former les fonctions booléennes que nous avons calculées. Les portes reçoivent l'entrée de la sortie des bascules et de l'entrée du circuit. N'oubliez pas de connecter l'horloge aux tongs !

La version D - Flip Flop :(Figure ci-dessous)

Le circuit séquentiel D - Flip Flop terminé

La version JK - Flip Flop :(Figure ci-dessous)

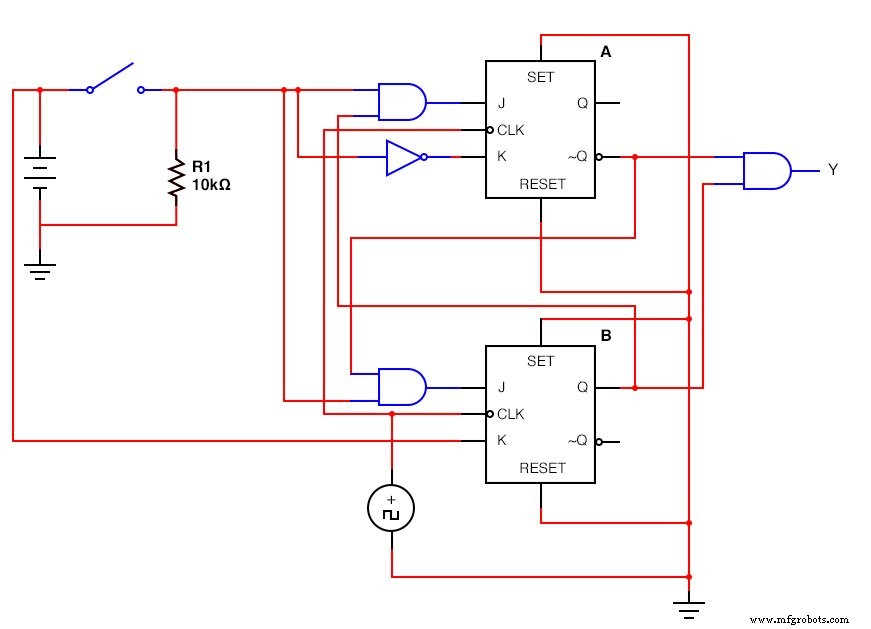
Le circuit séquentiel JK - Flip Flop terminé

Ça y est ...! Nous avons conçu et construit avec succès un circuit séquentiel. Au début, cela peut sembler une tâche intimidante, mais après la pratique et la répétition, la procédure deviendra triviale. Les circuits séquentiels peuvent être utiles en tant que parties de contrôle de circuits plus grands et peuvent effectuer n'importe quelle tâche de logique séquentielle à laquelle nous pouvons penser. Le ciel est la limite! (ou le circuit imprimé, au moins)

AVIS :

• Une fonction de logique séquentielle possède une fonction de « mémoire » et prend en compte les entrées passées afin de décider de la sortie.
• La machine à états finis est un modèle mathématique abstrait d'une fonction logique séquentielle. Il a des entrées, des sorties et un nombre d'états finis.
• Les FSM sont mis en œuvre dans des circuits réels grâce à l'utilisation de tongs
• La procédure de mise en œuvre nécessite un ordre spécifique d'étapes (algorithme) pour être exécutée.