Graphène HOT et nanotubes de graphène HOT :nouveaux semi-métaux et semi-conducteurs de faible dimension

Introduction

En raison de sa flexibilité de liaison, les systèmes à base de carbone présentent un nombre illimité de structures différentes avec une aussi grande variété de propriétés physiques. Ces propriétés physiques sont en grande partie le résultat de la dimensionnalité de ces structures [1]. Le graphène est une couche bidimensionnelle unique d'atomes de carbone liés dans une structure en réseau hexagonal [2] révélant un certain nombre de propriétés uniques, telles que des porteurs sans masse, une vitesse de Fermi élevée [3] et des cônes de Dirac [4, 5], qui sont caractéristique des fermions de Dirac bidimensionnels. Le réseau en nid d'abeille composé de deux sous-réseaux de carbone équivalents joue un rôle crucial dans la formation de ces propriétés intrigantes [2]. Enyashin et Ivanovskii [6] ont construit 12 réseaux de carbone artificiels 2D mais n'ont trouvé aucune structure autre que l'allotrope du graphène présentant le comportement électronique semblable au graphène. Cela semble impliquer que les fermions de type Dirac dans sp ² -les systèmes de carbone liés dépendent de la structure en nid d'abeille. Dans la dimension inférieure, le nanotube de carbone est une structure en nid d'abeille enroulée dans un cylindre creux de diamètre nanométrique et de longueur m [7,8,9,10]. Comme il existe une infinité de façons d'enrouler une feuille dans un cylindre, la grande variété de géométries hélicoïdales possibles, définissant la chiralité du tube, fournit une famille de nanotubes de diamètres et de structures microscopiques différents [11,12,13]. Les propriétés électroniques et de transport sont certainement parmi les propriétés physiques les plus importantes des nanotubes de carbone, et dépendent de manière cruciale du diamètre et de la chiralité [14,15,16,17,18]. Les nanotubes de graphène peuvent être soit semi-métalliques [14] soit semi-conducteurs [19,20,21], avec une bande interdite variant de zéro à quelques dixièmes d'eV, selon leur diamètre et leur chiralité [10, 14, 16]. De plus, on peut montrer que la bande interdite des tubes semi-conducteurs est simplement liée au diamètre du tube. Les nanotubes semi-métalliques conservent également les propriétés uniques du graphène, telles que les porteurs sans masse, la vitesse de Fermi élevée [22] et les cônes de Dirac [23]. De tels résultats remarquables peuvent être obtenus à partir d'une variété de considérations, à partir de l'approche dite de pliage de bande, basée sur la connaissance des propriétés électroniques de la feuille de graphène, à l'étude directe des nanotubes en utilisant des approches semi-empiriques de liaison serrée [14, 16, 18, 23]. Comparaison avec des calculs ab initio plus sophistiqués et des résultats expérimentaux disponibles, des considérations plus fines, telles que les effets de courbure, k _F le décalage [24, 25], l'hybridation σ-π [26] sont introduits. Le graphène et les matériaux similaires au graphène [6] sont considérés comme un matériau révolutionnaire pour la future génération de dispositifs électroniques à haute vitesse, logiques radiofréquences [27, 28], les composites renforcés thermiquement et électriquement [29, 30], le catalyseur [31], capteurs [32,33,34,35], électrodes transparentes [27, 36], etc. en se basant sur les propriétés inhabituelles ci-dessus. Au cours des dernières décennies, les nanotubes de carbone ont également montré un grand potentiel dans les circuits logiques, le stockage de gaz, la catalyse et le stockage d'énergie en raison de leurs propriétés électroniques, mécaniques et structurelles extraordinaires [37,38,39]. Ainsi, la création de nouveaux allotropes de carbone (y compris 2D et 1D) a fait l'objet de nombreuses explorations théoriques et expérimentales en raison de leur importance scientifique et technologique fondamentale [40]. Cependant, clarifier complètement les structures de ces phases carbonées excitantes grâce aux technologies expérimentales actuelles est généralement irréaliste en raison de leur quantité limitée, ainsi que du mélange d'autres phases. La prédiction théorique est nécessaire et a donné un grand succès [31,32,33,34,35, 40,41,42].

Dans cette étude, nous avons conçu un nouvel allotrope de graphène qui possède des fermions de Dirac bidimensionnels sans structure exclusivement hexagonale. Le nouvel allotrope a été construit avec des hexagones, octogones et tétragones de carbone entrelacés et a été nommé HOT graphène. CHAUD des nanotubes de graphène ont également été construits en enroulant HOT feuille de graphène avec différentes directions. La propriété électronique, l'effet de courbure, k _F effet de décalage, etc. de HOT le graphène et les nanotubes ont été calculés à l'aide de calculs ab initio basés sur la théorie de la fonction de densité (DFT).

Méthode de calcul

Les calculs actuels sur HOT graphène et CHAUD nanotubes de graphène ont été réalisés en utilisant une méthode des premiers principes basée sur la théorie de la fonctionnelle de la densité (DFT) avec l'approximation du gradient généralisé (GGA) sous la forme de la fonction d'échange-corrélation de Perdew-Burke-Ernzerh (PBE) [43], comme implémenté dans le Vienna Ab initio Simulation Package (VASP) [44, 45]. Les fonctions d'onde ont été étendues dans des ondes planes jusqu'à une coupure d'énergie cinétique d'onde plane de 520 eV. Les intégrales de la zone de Brillouin (BZ) ont été réalisées en utilisant un schéma d'échantillonnage de Monkhorst-Pack [46] avec un k -résolution du maillage en points de 2π × 0,03 Å ^− 1 . Les vecteurs de base des cellules unitaires (représentant la forme et la taille des cellules unitaires) et les coordonnées atomiques ont été complètement relâchés dans chaque système jusqu'à ce que les forces sur tous les atomes soient inférieures à 0,01  eV/Å.

Résultats et discussion

Structures géométriques et électroniques de HOT Graphène

La structure géométrique de HOT le graphène (Fig. 1a) montre une situation de liaison plus compliquée que le graphène. La variété des polygones de carbone dans HOT le graphène produit divers caractères de liaison au carbone. Ces polygones en HOT le graphène partage des arêtes communes les unes avec les autres et les liaisons peuvent être distinguées par les deux polygones auxquels elles appartiennent. Par conséquent, dans notre recherche, ils sont nommés 6-8 obligations, 4-8 obligations, 4-6 obligations, 6-6 obligations et 8-8 obligations. Les liaisons 4 à 8 et les liaisons 6 à 8 ont deux longueurs de liaison différentes :1,44  Å et 1,47  pour les liaisons 4 à 8 ; 1,41 Å et 1,48 Å pour 6 à 8 obligations. Les liaisons 4-6, 6-6 et 8-8 ont des longueurs de liaison uniques de 1,44 Å, 1,46 Å et 1,34 Å, relativement. La figure 1b montre la structure de bande et la densité d'états (DOS) de HOT graphène avec le BZ correspondant représenté sur la figure 1c. Le point de croisement des bandes d'énergie au niveau de Fermi indique une semi-métallicité de HOT graphène, ce qui est confirmé par la disparition du DOS au niveau de Fermi. Le point de Dirac est situé en (0, 0,0585, 0) adjacent à Γ. La structure de bande 3D (Fig. 2) présente les surfaces de bande près du niveau de Fermi, où l'on peut voir les cônes de Dirac formés par des surfaces coniques supérieure et inférieure se rencontrant en deux points de Dirac exactement à la surface de Fermi. La vitesse de Fermi correspondante (v_F ) des fermions de Dirac, évalué à partir du gradient des dispersions linéaires des structures de bandes, est de 6,27 × 10 ⁵ m/s, ce qui est un peu inférieur à 8,1 × 10 ⁵ m/s [22] pour le nanotube de graphène et 8,6 × 10 ⁵ m/s [47, 48] pour le graphène. Le haut v_F implique une grande mobilité des transporteurs dans le HOT graphène.

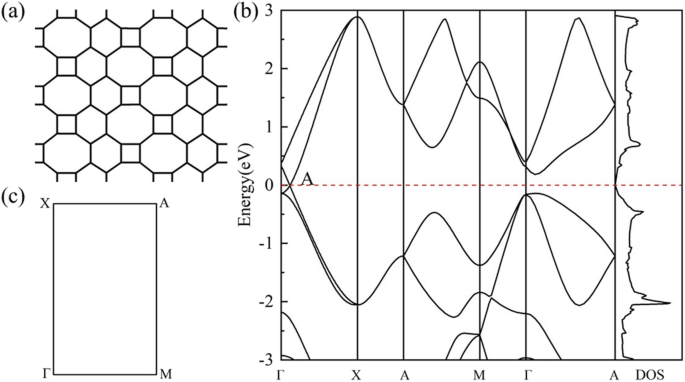
(un ) Géométrie de HOT graphène; (b ) Structures de bande et DOS du HOT graphène; (c ) le BZ correspondant de HOT graphène

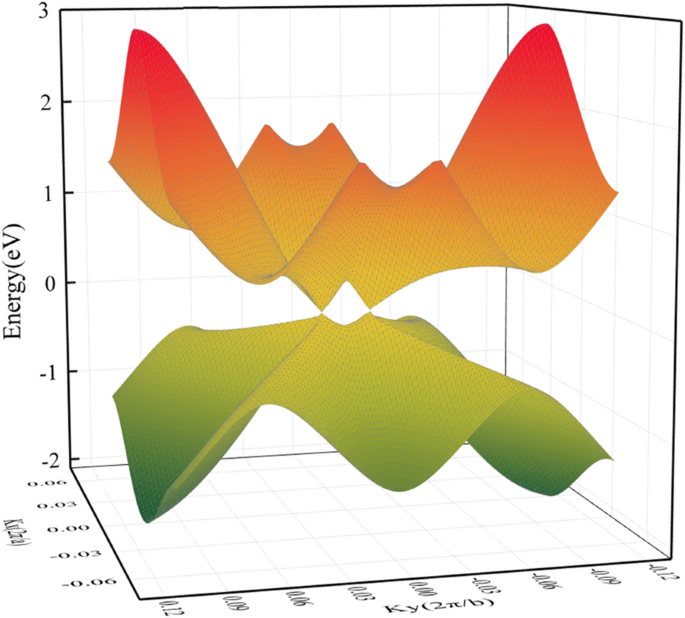
Structure de bande 3D du HOT graphène

Structures géométriques et électroniques de HOT Nanotubes de graphène

Le CHAUD Les tubes de graphène sont enroulés à partir du HOT feuille de graphène dans diverses directions symbolisée par un index sur le 2D HOT réseau de graphène (Fig. 3a). Cet indice est noté (l,m ) n en se basant sur deux vecteurs unitaires a et b . Symbole (l,m ) [18, 20, 21] signifie différentes directions sur le HOT feuille de graphène, n représente le nombre d'unités de périmètre (Fig. 3b et c) utilisées pour enrouler les tubes. Sous la symétrie d'inversion spatiale du HOT cellule unitaire de graphène, le symbole du nanotube est confiné à 0 ≤ l et 0 ≤ m pour éviter une correspondance plusieurs-à-un. Le nombre de structures géométriques possibles du HOT nanotubes de graphène est infini car il existe une infinité de choix pour les diamètres et les directions de laminage. Parmi un si grand nombre de nanotubes, seules deux directions (0,1, 1,0) sont retenues dans notre étude. C'est parce que l'arrangement hélicoïdal des atomes dans d'autres directions est à peine périodique et possède une longueur presque infinie de maille le long de l'axe du tube. Une cellule unitaire aussi grande est irréaliste dans notre calcul. Différentes directions de roulement entre (1,0) n et (0,1) n les tubes entraînent des différences de géométrie et de situation de collage. Deux tubes, (1,0)6 et (0,1)4, sont représentés sur les Fig. 3d et e pour décrire les différences géométriques entre les deux sens de roulement. La disposition des polygones dans la direction (1,0) peut être divisée en deux modèles :C₄ –C₆ –C₈ (orange) et C₈ –C₆ –C₄ (bleu) qui sont exactement opposés l'un à l'autre. Ces deux motifs opposés alternent le long de la direction circonférentielle du tube. Dans la direction (0,1), les polygones disposés le long de l'axe du tube ont également deux motifs :C₄ –C₈ (bleu) et C₆ –C₆ (Orange). Deux C₄ –C₈ les motifs alternent avec un C₆ –C₆ motif le long de la direction circonférentielle.

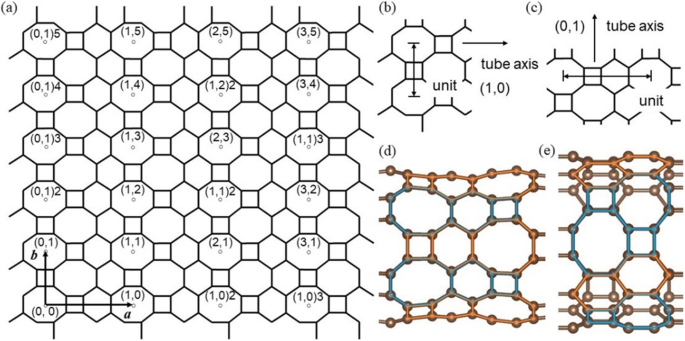
(un ) Les différents tubes sont signalés par le symbole (l,m ) n , avec (l,m ) représente la direction de roulement basée sur le vecteur unitaire a et b , et n pour le nombre d'unités de diamètre de tube ; (b ) unité de diamètre dans la direction (1,0) ; (c ) unité de diamètre dans la direction (0,1) ; (d ) structure géométrique d'un (1,0)6 CHAUD nanotube de graphène; (e ) structure géométrique d'un (0,1)4 CHAUD nanotube de graphène

Pour révéler le coût énergétique de l'enroulement d'une tôle en tubes, nous définissons l'énergie de courbure (Fig. 4) E _cur comme :

où \( {E}_{\mathrm{tube}}^{\mathrm{at}} \) est l'énergie moyenne des atomes dans le nanotube, et \( {E}_{\mathrm{sheet}}^{\ mathrm{at}} \) est l'énergie moyenne des atomes dans la feuille 2D. Le (1,0) n les tubes présentent un coût énergétique inférieur à celui des nanotubes de graphène tandis que le (0,1) n les tubes sont presque les mêmes que les nanotubes de graphène fauteuil, à l'exception de plusieurs tubes ultra-petits. De tels résultats suggèrent également qu'il est possible de synthétiser le HOT nanotubes de graphène dans les expériences. Il est à noter que le tube (1,0)1 est trop petit car son diamètre est encore plus court que la longueur de liaison du carbone.

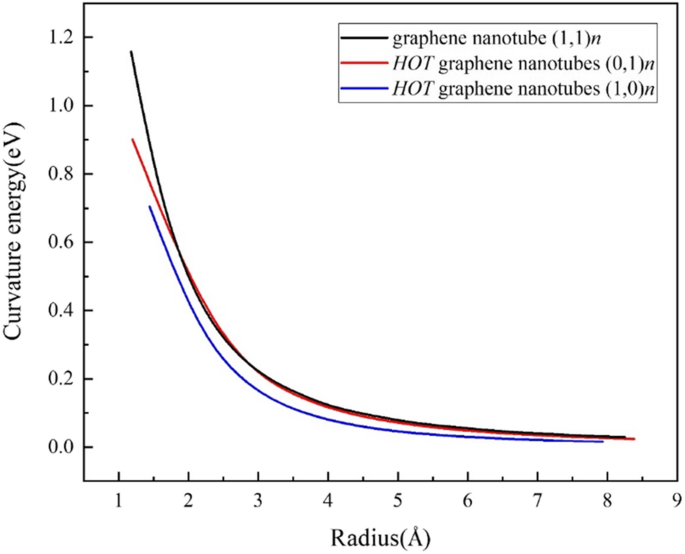
Énergies de courbure du HOT nanotubes de graphène et nanotubes de graphène

La structure de bande électronique calculée et le DOS du nanotube (0,1)6 (Fig. 5b) indiquent un caractère semi-métallique. Lorsque le CHAUD feuille de graphène est enroulée dans un nanotube, son BZ 2D se réduit à BZ 1D en raison des nouvelles conditions aux limites périodiques dans les nanotubes. Les conditions aux limites périodiques le long de la direction circonférentielle du tube n'autorisent que des vecteurs d'onde « autour » de la circonférence du nanotube et ces vecteurs sont quantifiés [49]. Les conditions aux limites périodiques le long de l'axe des nanotubes restent les mêmes que la feuille 2D, puis les vecteurs d'onde restent continus le long de l'axe des nanotubes. Selon le schéma de pliage de zone, la structure de bande électronique d'un nanotube spécifique est donnée par la superposition des bandes d'énergie électronique de la feuille 2D correspondante le long du k spécifiquement autorisé. lignes [50]. En tant que vecteurs d'onde quantifiés au milieu du BZ du HOT le graphène traverse toujours le point de Dirac (point F sur la Fig. 5a), un point de Dirac non dégénéré (point F sur la Fig. 5b) et le cône de Dirac apparaît dans les structures de bande du (0,1) n HOT nanotubes de graphène, résultant en la semi-métallicité de tous les (0,1) n nanotubes. Le tube (0,1)6 est calculé pour évaluer la semi-métallicité de cet ensemble de (0,1) n nanotubes dans la Fig. 5. Structure de bande du (0,1)6 HOT les nanotubes de graphène montrent un point de croisement de bandes d'énergie au niveau de Fermi et le DOS correspondant ne montre aucun état au niveau de Fermi qui vérifie la semi-métallicité du système. Comme le cône de Dirac en (0,1) n tubes est originaire du HOT feuille de graphène, la coordonnée calculée du point de Dirac dans le nanotube (0,1)6 est la même que celle dans HOT feuille de graphène qui est (0, 0,0585, 0). La vitesse de fermi calculée au point de Dirac dans (0,1)6 nanotube est de 6,76 × 10 ⁵ m/s, proche de 6,27 × 10 ⁵ m/s dans le CHAUD feuille de graphène.

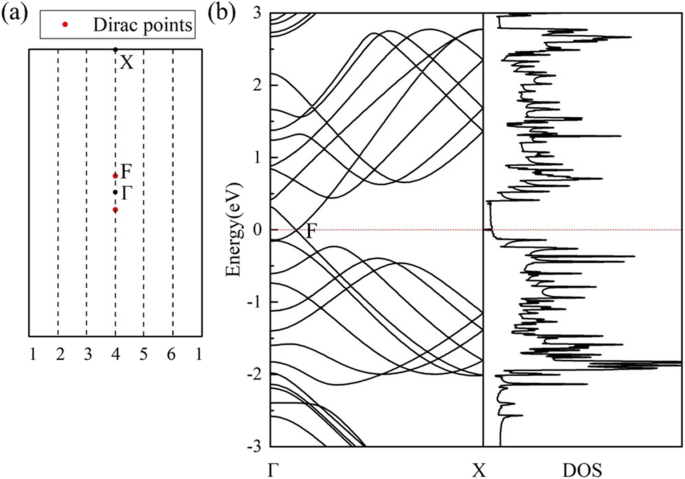
(un ) Le premier BZ du HOT graphène avec k autorisé lignes (traits pointillés) pour le nanotube (0,1)6. F est le point de Dirac. (b ) Les structures de bandes calculées et DOS de (0,1)6 nanotube

L'évolution de la structure de bande de (0,1) n nanotubes avec des rayons de tube différents (Fig. 6a) révèle que le CHAUD nanotubes de graphène (0,1) n sont semi-métalliques (n ≥ 3) et transformer en métal (n = 2) puis revenez au semi-métal (n = 1). Un tel changement sous un petit rayon résulte de ce que l'on appelle l'effet de courbure [26]. Dans le cas de nanotubes ultra-petits (par exemple, (0,1)2 et (0,1)1), la courbure a un effet non négligeable sur le schéma de repliement de zone. La longueur de liaison et l'angle de liaison subissent un changement non négligeable au sein de la grande courbure, ce qui a une influence sur la structure de la bande électronique. Les structures de bandes de tels nanotubes ne sont plus une simple superposition de bandes d'énergie sur les vecteurs d'onde autorisés. Ce changement de liens modifie les conditions qui définissent le k point auquel les bandes occupées et inoccupées se croisent (à un point que nous étiquetons k _F ) et décalez le k _F loin des points de Dirac d'origine, qui s'appelle le k _F effet de déplacement [24, 25]. En conséquence, dans le (0,1) n HOT nanotubes de graphène, les k _F s'éloigne de sa position d'origine (k _CHAUD ) dans le CHAUD feuille de graphène (point F sur la figure 5a). Et le changement de direction de k _F est calculé pour être le long du vecteur d'onde autorisé (lignes pointillées sur la Fig. 5a), ce qui n'entraîne aucun changement de la semi-métallicité (Fig. 6a (n 3)). D'après la coordination calculée des points de Dirac, le k _F l'effet de décalage devient non négligeable à (0,1)5 avec un rayon de tube de 5.988 Å, dont le point Dirac (k _F ) passe à (0,0.0626.0) à partir du point d'origine (k _CHAUD ) à (0,0.0594,0) dans CHAUD feuille de graphène. Au fur et à mesure que le rayon du tube diminue, le k _F continue de se déplacer et atteint le point (0,0.0712,0) dans le tube (0,1)3. Dans le tube (0,1)2, le k _F passe à (0,0.0835,0) où le point de Dirac descend en dessous du niveau de Fermi, résultant en un système métallique. La disparition de la semi-métallicité en (0,1)2 indique un écart par rapport au k _F effet de décalage dans (0,1) n nanotubes (n 3). De plus, le tube (0,1)1 redevient semi-métallique dans sa structure de bande et le DOS (Fig. 6b). Notre analyse de l'état électronique du (0,1) n HOT nanotubes montre π états se chevauchant à n ≥ 2, qui est généralement considéré comme l'origine de la semi-métallicité des nanotubes de graphène [18, 24]. Cependant, l'analyse de l'état électronique correspondante du HOT Le nanotube de graphène (0,1)1 montre une hybridation σ-π selon laquelle une bande * basse coupe le niveau de Fermi et rejoint le cône de Dirac (lignes bleues sur la Fig. 6a). La coordination du point de Dirac, qui est (0,0.18345,0), se distingue également des autres (0,1) n HOT nanotubes de graphène. La vitesse de Fermi calculée est de 4,47 × 10 ⁵ m/s, inférieur à 6,27 × 10 ⁵ m/s en CHAUD feuille de graphène et valeurs pour les autres (0,1) n nanotubes (~6,76 × 10 ⁵ Mme). Une forme évidemment différente de sa structure de bande est également illustrée sur la figure 6a. Tous ces caractères vérifient que la semi-métallicité du HOT Le nanotube de graphène (0,1)1 est issu de l'hybridation σ-π. En résumé, avec la courbure croissante, le k _F l'effet de changement apparaît à n = 5, devient plus efficace à 4 ≥ n ≥ 2, et est finalement remplacé par l'effet d'hybridation σ-π à n = 1.

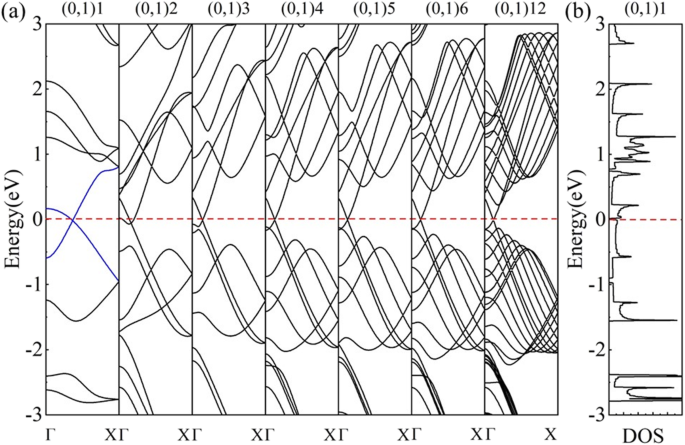
(un ) Évolution de la bande de (0,1) n nanotubes (n = 1, 2, 3, 4, 5, 6, 12); (b ) DOS du (0,1)1 nanotube

Dans une autre direction de roulement, la structure de bande calculée de (1,0)6 (Fig. 7b) montre une semi-conductivité. Les 6 vecteurs d'onde (lignes tiretées) sont parallèles à Γ-M, croisant le point Г au milieu de la BZ de HOT graphène (Fig. 7a) et ouvrir une bande interdite de 0,46  eV comme indiqué dans le DOS (Fig. 7b). Dans ce sens de roulement, les vecteurs d'onde autorisés au milieu de la BZ n'incluent jamais les points de Dirac, ce qui se traduit par des bandes interdites non nulles dans cet ensemble de nanotubes. L'évolution de la bande révèle un changement des bandes interdites avec des rayons différents sur la Fig. 8a. Le (1,0) n CHAUD les nanotubes de graphène sont semi-conducteurs (n 4). Le maximum de bande de valence (VBM) et le minimum de bande de conduction (CBM) se rapprochent du tube (1,0)6 au tube (1,0)4 puis se croisent dans le tube (1,0)3 avec un rayon de 2.17 Å. Ce point de passage se trouve exactement au niveau de Fermi situé à (0,0791,0,0). Le DOS calculé (Fig. 8b) présente 0 états au niveau de Fermi de (1,0)3, vérifiant la semi-métallicité. Lorsque le rayon du tube diminue à (1,0)2, un espace de 0,848  eV s'ouvre à nouveau. Le CBM et le VBM de (1,0)2 sont situés respectivement au point Γ et au point M, indiquant une bande interdite indirecte. Ce changement de VBM implique une origine différente pour la semi-conductivité dans (1,0)2. Une étude plus approfondie du changement de bande interdite dans le (1,0) n HOT Les nanotubes de graphène sont illustrés à la Fig. 9. L'évolution de la bande interdite en fonction de n (3 ≤ n ≤ 23) indique que la bande interdite est réglable avec les tailles de tube. De plus, au lieu d'être monotone, la dépendance de la bande interdite à la taille du tube a une forme en zigzag (figure 9 courbe noire). Le minimum global à (1,0)15 présente une bande interdite nulle. La semi-métallicité de (1,0)15 est en outre confirmée par la structure de la bande et le DOS (Fig. 9g). A partir du schéma de pliage de zone, nous savons que la structure de bande des nanotubes est la superposition de la structure de bande de la feuille 2D le long du k quantifié correspondant lignes [50]. Ainsi, la semi-métallicité indique qu'au moins un des k autorisés lignes (traits pointillés sur la figure 7a) coupent les points de Dirac (points rouges sur la figure 7a) à n =  15. Sinon, si le k autorisé les lignes ont une distance des points de Dirac (k _CHAUD ), une bande interdite apparaîtra dans le nanotube. De plus, cette distance entre k _F et le k est proportionnelle aux bandes interdites, car la dispersion des bandes près du cône de Dirac est linéaire [25]. Le Δk _m mesure la distance la plus courte entre k _F et k _m lignes de nombre quantique m . Nous avons calculé cette distance Δk _m entre les pointes de Dirac (k _CHAUD ) et les k autorisés lignes dans le HOT graphène et tracez-le (ligne rouge) avec les bandes interdites (ligne noire) sur la figure 9. Premièrement, tous les k autorisés les lignes ont un nombre quantique m . Lorsque n ≤ 7 ​​(par exemple, Fig. 9a), la distance la plus courte (Δk _m ) est entre le k _CHAUD et le premier k ligne, k ₁ , qui se trouve constamment au point Γ (insérer le graphique (a) sur la figure 9). Dans cette situation, Δk _m est constant car à la fois k ₁ et k _CHAUD sont des constantes indépendantes de la taille du tube. Cependant, comme le k autorisé les lignes se densifient dans les nanotubes plus gros (7 ≤ n ≤ 17), le k ₂ devient le plus proche de k _CHAUD (par exemple, la figure 9b). Dans cette situation, le k ₂ approche le point de Dirac depuis la BZ externe avec des rayons de tube croissants ; par conséquent, il montre une baisse de Δk _m dans la Fig. 9 (7 ≤ n 17). n = 17 est un tournant où k ₂ coupe presque le point de Dirac résultant en un minimum local de la distance Δk _m (Fig. 9c). Au fur et à mesure que le rayon augmente, le k ₂ traverser le k _CHAUD point et continue de s'en éloigner jusqu'au point Г, ce qui entraîne une nouvelle augmentation de la distance à 17 ≤ n ≤ 24 (par exemple, Fig. 9d). En même temps, k ₃ approche de la pointe de Dirac. k ₃ se rapproche de k _CHAUD que k ₂ et commence une nouvelle diminution de distance Δk _m à n ≥ 24. Comme les bandes interdites sont proportionnelles à cette distance Δk _m [25], la courbe de bande interdite montre la même forme que le Δk _m tracé (n 7). Et il est révélé que les bandes interdites changent au cours des cycles :le k _m se rapproche de la pointe de Dirac (k _CHAUD ) provoquant une baisse de la bande interdite, puis traverse le point de Dirac entraînant un minimum local, puis s'éloigne du point de Dirac provoquant une hausse de la bande interdite, et est finalement remplacé par la ligne suivante k _m + 1 entrer dans le cycle suivant. En résumé, la raison pour laquelle les bandes interdites changent avec la taille du tube (n ≥ 7) est que le k les lignes se déplacent avec différentes tailles de tubes, ce qui modifie la distance Δk _m entre k _CHAUD et les k autorisés lignes proportionnelles aux bandes interdites.

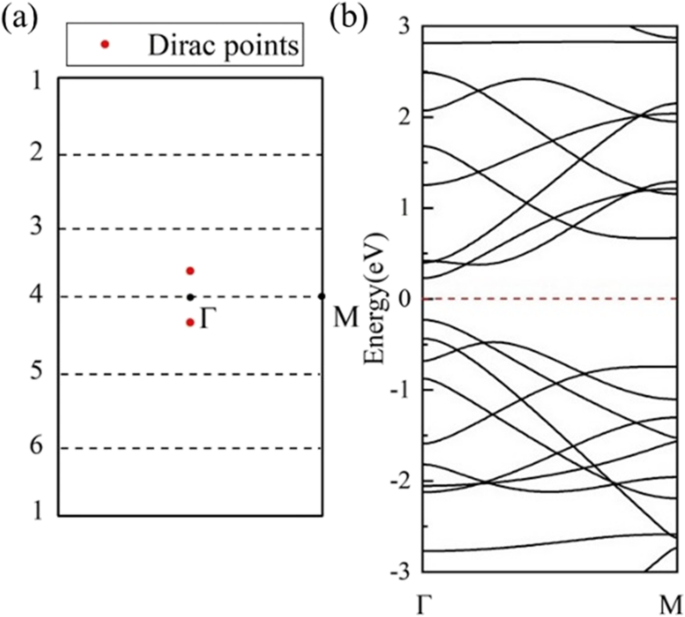
(un ) Le premier BZ du HOT graphène avec k autorisé des lignes (tirets) pour le nanotube (1,0)6 ; (b ) structures de bande du (1,0)6 nanotube

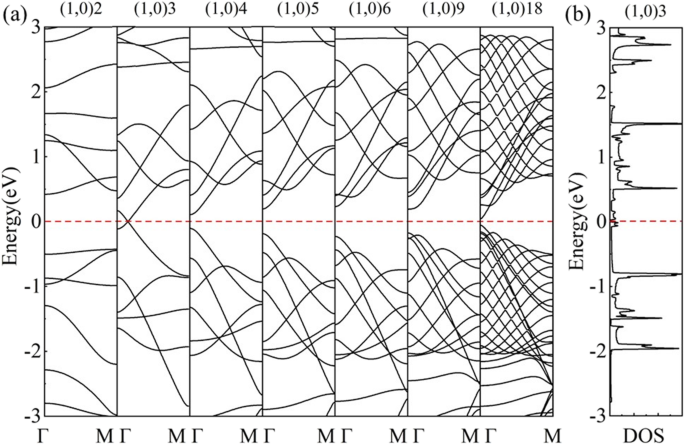
(un ) Évolution de la bande de HOT nanotubes de graphène (1,0) n (n = 2, 3, 4, 5, 6, 9, 18); (b ) DOS du (1,0)3 nanotube

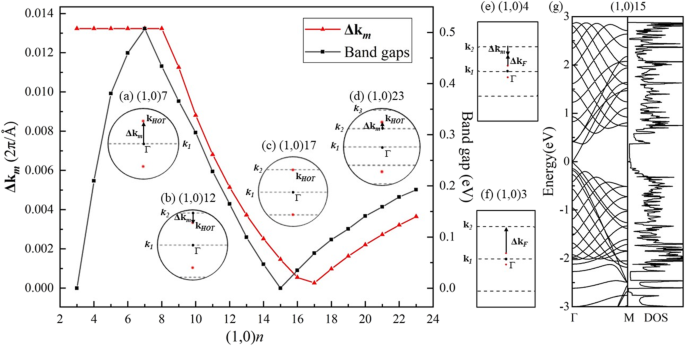
Bandes interdites calculées (ligne noire) et distance Δk _m (ligne rouge) entre k _CHAUD et le k le plus proche ligne dans (1,0) n tuyaux. Les graphiques insérés sont les BZ près du point Γ avec les k autorisés lignes k _m (m = 1, 2, 3) (lignes tiretées) et le point de Fermi de HOT nanotubes de graphène k _CHAUD (points rouges) en tube (a ) (1,0)7, (b ) (1,0)12, (c ) (1,0)17, (d ) (1,0)23, (e ) (1,0)4, et (f ) (1,0)3. (g ) Structures de bande et DOS du tube (1,0)15

Bien que le Δk _m et la courbe de bande interdite ont des similitudes de forme, les différences entre elles sont également évidentes, c'est-à-dire que le Δk _m le graphique montre un « retard » dans le changement à n ≥ 7 et devient complètement différent du tracé de la bande interdite à 3 ≤ n ≤  7. La raison en est que le point de Fermi dans HOT nanotubes de graphène (k _F ) est supposé avoir la même coordonnée que le point de Fermi d'origine dans HOT graphène (k _CHAUD ) dans la section précédente où le changement de bande interdite a été expliqué. Cependant, le point de Fermi (k _F ) dans les nanotubes s'éloigne du point de Fermi d'origine (k _CHAUD ) dans CHAUD feuille de graphène sous l'effet de courbure. Par conséquent, le k _F décalage (Δk _F = k _F –k _CHAUD ) contribue aux discordances entre la distance Δk _m et les bandes interdites. Tel que calculé dans (0,1) n tubes (Fig. 6), les k _F dans (1,0) n tubes se déplace également vers le BZ externe vers le point symétrique X sous la courbure. Par conséquent, lorsque le k le plus proche _m se trouve entre le k _CHAUD et le point Γ, la distance Δk _m sous-estime la bande interdite (par exemple, 17 ≤ n ≤ 24 sur la figure 9d). Sinon, le k le plus proche _m assis à l'extérieur du k _CHAUD point, il en résulte une surestimation de la bande interdite (par exemple, 7 ≤ n ≤ 17 sur la figure 9b). Dans de petits nanotubes (3 ≤ n ≤ 7), le k _F l'effet de déplacement est amélioré sous le grand taux de croissance de la courbure ; par conséquent, cela provoque un k drastique _F décalage et modifie la bande interdite. Lorsque le rayon devient plus petit que n = 8, le k ₁ devient le plus proche du k _CHAUD indiquant une constante Δk _m . Cependant, le k _F l'effet de décalage est si fort pour déplacer le k _F plus loin de k ₁ mais plus proche du k ₂ (Fig. 9e). Le k _F Shifting effect remporte la compétition avec le k les lignes bougent et commence à déterminer les bandes interdites depuis lors (n 7). Le k _F continue de passer au k ₂ à grande vitesse de sorte que la distance entre k _F et k ₂ devient de plus en plus petit. Par conséquent, de (1,0)7 à (1,0)3, la bande interdite diminue (Fig. 9). Enfin, le k _F rattrape k ₂ et le traverse à n = 3(Fig. 9f). Ce croisement d'un k ligne avec le k _F aboutit au point de Dirac dans le tube (1,0)3 qui donne lieu à la semi-métallicité (Fig. 8) comme discuté dans les sections précédentes. Nouvelle diminution du rayon à n = 2 ouvre un espace de 0,848 eV dans le tube (1,0)2 (Fig. 8). Cet écart est si grand et est considéré comme hors du k _F schéma de déplacement, et n'est donc pas représenté sur la figure 9. En résumé, il existe un mécanisme de concurrence entre les k la ligne bouge et le k _F décalage dans la détermination des bandes interdites. Le k _F effet de déplacement conduit dans de petits tubes (7 ≥ n ≥ 3), tandis que le k fils de déplacement de ligne dans de gros tubes (n ≥ 8) où le k _F l'effet de décalage est atténué. Le montant du k _F le décalage est estimé à 0,0015 2π/Å à n = 15 et 0,0238 2π/Å à n = 3 car les bandes interdites sont de 0 eV où le k décalé _F le point est sur le k autorisé lignes. On peut voir que le k _F le décalage est 15,86 fois plus important dans un petit tube (tube (1,0)3) que dans un gros tube (tube (1,0)15).

Dans CHAUD graphène, les atomes de carbone sont tous trois fois coordonnés, ainsi le quatrième électron de valence joue un rôle clé dans sa conductivité. The calculated band decomposed charge density ± 0.15 eV around the Fermi level (Fig. 10) shows the distribution of the electrons in the Dirac cone. Only the electrons on the 8–8 bonds (Fig. 10a) have an overlapping and the side view (Fig. 10b) shows that the electrons distribute perpendicularly to the HOT graphene sheet, which indicates that the Dirac cone consists of π states. Therefore, the electron overlapping on the 8–8 bonds (enlarged side view in Fig. 10a) is considered to be localized π states. In big nanotubes such as (0,1)6 (Fig. 10c), the charge density is similar to the HOT graphene sheet showing localized π bonds on 8–8 bonds (enlarged side view in Fig. 10c). As the radius decreases to (0,1)2, whose conductivity transforms to metal (Fig. 6), the 8–8 bonds show several deformations (Fig. 10d). Firstly, these states are no longer symmetric with respect to the tube wall. The overlapping of the π state outside the tube wall breaks apart while the π states inside keep overlapping with each other. Besides the 8–8 π bonds, new π bonds form on 4–8 in (0,1)2. These bonds are similar to the deformed 8–8 bonds:separated π states outside the tube wall and overlapping π states inside the tube wall. Every 4–8 bond connects two 8–8 bonds adjacent to it, forming a delocalized π overlapping inside the tube along the tube axis direction. The enlarged side view in Fig. 10d shows the connection between 4 and 8 and 8–8 bonds as a segment of the whole delocalized bond. Therefore, the metallicity in tube (0,1)2 can be attributed to the delocalized π overlapping in the 4–8 and 8–8 bonds along the tube axis direction which provides a pathway for the electrons to travel along the tube. When the radius keeps decreasing, the conductivity disappears and the (0,1)1 tube becomes a semimetal again (Fig. 6). Different from all the other (0,1) n tubes, the 8–8 overlapping (Fig. 10e) in nanotube (0,1)1 is totally broken up; instead, 4–8 overlapping and 4–6 overlapping plays the major role in the Dirac cones. These two bonds belong to two opposite edges in the same carbon tetragons and are arranged parallel to the tube axis. Furthermore, they are no longer π states. Based on the electronic state analysis, a σ-π hybridization takes place at the Fermi level under such a strong curvature in nanotube (0,1)1. It is verified by the charge density which shows the electron states distribute closely to the bond axis (enlarged side view in Fig. 10e). Strongly modified low-lying σ states are introduced at the Fermi level as discussed in the preceding sections (blue line in Fig. 6). Therefore, the σ-π hybrid states in the 4–8 and 4–6 bonds are considered the reason for the semimetallicity in (0,1)1, which is essentially different from the other semimetallic tubes (0,1) n (n  ≥ 3). In another set of HOT graphene nanotubes, the band gaps show adjustability with different tube radius (Fig. 9). The charge densities also present an evolution with the tube radii in Fig. 11. The band decomposed charge density of tube (1,0)9 in Fig. 11a and b shows the localized π states overlapping in both the VBM and CBM. The VBM is contributed by π states on 6–6 bonds and 8–8 bonds (Fig. 11a). The CBM is contributed by π states on part of 4–8 and 6–8 bonds (Fig. 11b). The 4–6 bonds have no states on both of the VBM and CBM. When the (1,0) n tubes become semimetallic at some specific radii, such as n  = 15, the VBM and CBM meet with each other. Band decomposed charge density ± 0.15 eV around the Fermi level of (1,0)15 nanotube show the different distribution of electrons from the semiconductive tubes. More importantly, it exhibits a similar distribution to the semimetallic HOT graphene sheet and (0,1) n tubes. The localized π bond of (1,0)15 only locates on the 8–8 bonds. This redistribution of electron in (1,0) n tubes causes the conductivity change.

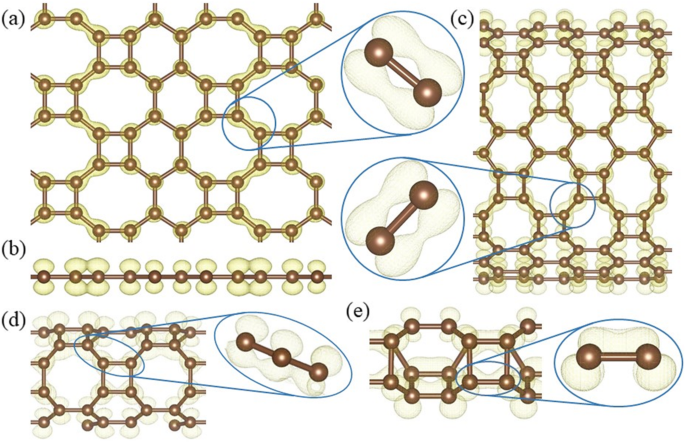
Band decomposed charge densities around the Fermi level of (a ) HOT graphene, (b ) the corresponding side view, and HOT graphene nanotubes (c ) (0,1)6, (d ) (0,1)2, and (e ) (0,1)1 with corresponding enlarged side views

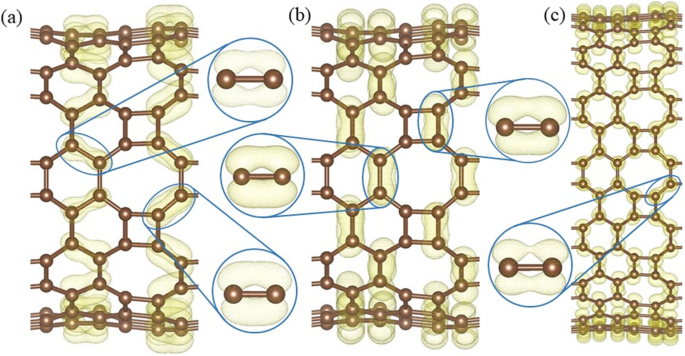
Band decomposed charge densities at (a ) VBM, and (b ) CBM of HOT graphene nanotube (1,0)9; (c ) charge densities around the Fermi level of the HOT graphene nanotube (1,0)15 with the localized π bond in the enlarged side view

Conclusion

A new graphene allotrope named HOT graphene is constructed by carbon hexagons, octagons, and tetragons showing Dirac cone and high Fermi velocity, which implies that the honeycomb structure is not an indispensable condition for Dirac fermions to exist. The semiconductivity of HOT graphene is dependent on the localized π bonding. A corresponding series of nanotubes is rolled up from the HOT graphene sheet and shows distinctive electronic structures depending on the topology. The set of (0,1) n (n  ≥ 3) HOT graphene nanotubes reveals a character of semimetallicity and Dirac cones that are composed by π states. A non-negligible k _F shifting along the allowed k line arises under the curvature effect when the tube radius gets smaller (3 ≤ n  ≤ 5). However, the ultra-small nanotube (0,1)2 begins to deviate from the π state-based k _F shifting effect showing a transformation to metallicity. Finally, an σ-π hybridization takes the place of the π states at Fermi level in nanotube (0,1)1, where a low-lying σ* band intersection appears at the Fermi level and forms a semimetallicity again. Another set of tubes (1,0) n shows various band gaps (0~ 0.51 eV), which is continuously adjustable with the tube size. The band gaps of (1,0) n (n  ≥ 3) nanotubes turn out to be determined by a competition mechanism between the k line moving and the k F shifting effect. The zone-folding approximation indicates a k line moving and results in the zigzag and periodical band gap changing curve in big tubes (n  ≥ 8), while the k F shifting effect gets stronger and causes a dramatic decrease of band gaps in small tubes (7 ≥ n  ≥ 3). Zero-gap semimetallic tubes appear periodically under the competition.

Disponibilité des données et des matériaux

Authors declare that the datasets used and/or analyzed during the current study are available to the readers and included in this article.

Abréviations

1D:

One-dimensional

2D:

Bidimensionnel

3D:

Three-dimensional

BZ:

Brillouin zone

CBM:

Conduction band minimum

DFT:

Density functional theory

DOS:

Density of states

GGA:

Generalized-Gradient Approximation

HOT :

Hexagons, octagons, and tetragons

PBE:

Perdew–Burke–Ernzerh

VASP:

Vienna Ab initio Simulation Package

VBM:

Valence band maximum