Propriétés de la phase géométrique dans les oscillations électromécaniques des résonateurs à nanofils à base de nanotubes de carbone

Résumé

La phase géométrique est une évolution de phase supplémentaire dans la fonction d'onde des vibrations qui est potentiellement applicable dans un large éventail de sciences et de technologies. Les caractéristiques de la phase géométrique à l'état comprimé pour un résonateur à nanofils à base de nanotubes de carbone ont été étudiées au moyen de la méthode de l'opérateur invariant. L'introduction d'un opérateur invariant linéaire, utile pour traiter un système hamiltonien compliqué dépendant du temps, nous a permis de dériver la formule analytique de la phase géométrique. En utilisant cela, nous avons analysé le comportement temporel de la phase géométrique sur la base d'illustrations pertinentes. L'influence des paramètres de compression sur l'évolution de la phase géométrique a été étudiée. La phase géométrique, en gros, oscille, et l'enveloppe d'une telle oscillation augmente avec le temps. Le taux d'augmentation de la phase géométrique est grand lorsque les paramètres, tels que l'amplitude classique de l'oscillation, le facteur d'amortissement et l'amplitude de la force motrice, sont grands. Nous avons confirmé une très forte augmentation de la phase géométrique au cours du temps dans le cas où la fréquence angulaire du système atteint près de la fréquence angulaire de résonance. Notre développement concernant les caractéristiques de la phase géométrique est crucial pour comprendre les caractéristiques topologiques des oscillations des nanofils.

Introduction

Les vibrations mécaniques des plus petits résonateurs, tels que les nanofils à base de nanotubes de carbone (à base de CNT) [1–3], les nanofils semi-conducteurs [4], les graphènes [5] et les particules en lévitation [6], ont été un sujet de recherche principal dans la communauté des nanosciences depuis plus d'une décennie. Des recherches actives concernant les oscillations électromécaniques des résonateurs à nanofils entraînés par une force périodique externe ont été menées dans les domaines théorique et expérimental. En particulier, les résonateurs à nanofils à base de CNT ont suscité un intérêt considérable en tant que dispositifs mécaniques à l'échelle nanométrique en raison de leurs sensibilités extraordinaires avec des facteurs de haute qualité à une petite perturbation de l'environnement. Les résonateurs à nanofils suspendus à base de NTC sont des candidats prometteurs pour les appareils mesurant une large gamme de grandeurs physiques, telles que les ondes électromagnétiques [2], les petites forces [7], les masses [8], les températures [9] et les bruits [10].

Des analyses de l'évolution de la phase quantique dans les oscillations des nanofils sont nécessaires pour élucider théoriquement les caractéristiques sous-jacentes du système. Concernant les états vibrationnels quantiques des résonateurs à nanofils à base de CNT [11], la phase géométrique [12] ainsi que la phase dynamique habituelle apparaissent comme une évolution supplémentaire de la phase. La phase géométrique [12] est une anholonomique d'un état quantique qui peut être applicable dans divers domaines de la physique. Les analyses de la phase géométrique peuvent être potentiellement adoptées pour caractériser les propriétés nano des nanofils, telles que les profils de résonance [13, 14], les fortes vibrations quantiques [15, 16], les mécanismes de relaxation des contraintes [17, 18], l'émergence des magnétoplasmons de Dirac [19], et la topologie des oscillations Aharonov-Bohm [20].

L'étude de la phase géométrique associée à la dynamique non adiabatique peut fournir un aperçu des systèmes nanomécaniques, ce qui est nécessaire pour l'avancement des techniques de simulation précises [21]. La préparation, la manipulation et la détection des états quantiques sont des facteurs importants dans les technologies quantiques. L'objectif de la présente recherche est de faire la lumière sur les comportements temporels de la phase géométrique qui se déroule dans les états quantiques des oscillations des nanofils. Pour comprendre le mécanisme des vibrations des nanofils à base de CNT, nous étudierons l'évolution temporelle de la phase géométrique dans l'état comprimé qui est un état quantique de type classique comme l'état cohérent. Le mérite de l'état compressé est que l'incertitude d'une quadrature dans cet état peut être considérablement réduite au détriment de l'augmentation de l'incertitude de l'autre quadrature, alors qu'une telle modulation d'incertitude est impossible dans l'état cohérent. En particulier, nous analyserons les effets de la résonance sur la phase géométrique. Parce que l'énergie résonante est significativement différente de l'énergie de l'état non résonant [22, 23], le comportement topologique de la fonction d'onde n'est pas trivial et peut être considérablement dévié de celui dans des situations normales. L'influence du changement des paramètres physiques et des paramètres de compression sur l'évolution de la phase géométrique sera également rigoureusement analysée. Les phases géométriques sont omniprésentes dans les systèmes dynamiques [24] et peuvent être appliquées à diverses technologies modernes, telles que le calcul quantique [25], les interférométries d'intensité [26], le multitâche photonique [27], les protocoles de détection quantique [28] et les ondes. -mesures de stabilité [29].

L'hamiltonien du système fait intervenir des fonctions temporelles associées à l'amortissement du système et à la force motrice externe. Par conséquent, le système est une sorte de systèmes hamiltoniens dépendant du temps (TDHS) dont les problèmes de mécanique quantique ont été largement étudiés jusqu'à récemment. La fonction de temps dans l'hamiltonien d'un TDHS ne peut pas être séparée de la fonction de variables canoniques dans la plupart des cas, ce qui conduit à l'indisponibilité de la méthode conventionnelle de séparation des variables pour résoudre l'équation de Schrödinger. Une méthode alternative puissante développée pour surmonter cette difficulté est la méthode de l'opérateur invariant qui a été introduite par Lewis et Riesenfeld [30, 31]. Cette méthode est un outil mathématique très utile lorsque nous dérivons des solutions quantiques d'un TDHS. De nombreux problèmes de mécanique quantique décrits par les TDHS sont étudiés sur la base de cette méthode. Par exemple, ils incluent la diffusion chaotique des particules [32], la propagation de la lumière dans des milieux variant dans le temps [33], le contrôle des électrons entraînés piégés [34] et la non-classicité des circuits nanoélectroniques quantiques [35]. Il existe une variété d'autres méthodes pour les traitements mécaniques quantiques des TDHS, notamment la méthode de transformation unitaire [36], la méthode algébrique de Lie [37] et la méthode d'estimation hamiltonienne [38].

Considérant que le système est un TDHS, nous utilisons la méthode de l'opérateur invariant afin d'obtenir des solutions quantiques du système. Un opérateur invariant linéaire qui est représenté en termes d'opérateur d'annihilation sera introduit. Alors que les opérateurs d'annihilation et de création sont représentés en termes de temps en raison de la dépendance temporelle du système, les états cohérent et comprimé peuvent être obtenus à l'aide de ces opérateurs d'échelle. La phase géométrique du système sera évaluée analytiquement en utilisant la fonction d'onde à l'état comprimé. L'évolution temporelle de la phase géométrique sera analysée en détail sur la base de ses illustrations représentées avec divers choix de paramètres.

Méthodes

Pour étudier la phase géométrique, nous devons d'abord configurer l'équation classique du mouvement de la pointe du nanofil. Parce que la phase géométrique apparaît dans l'évolution d'onde quantique d'un TDHS, il est nécessaire de dériver des fonctions d'onde dans un état quantique spécifique que nous gérons. Nous considérerons l'état compressé tel que mentionné dans la partie introductive. Les fonctions d'onde dans les divers états quantiques d'un TDHS, y compris l'état compressé, peuvent être obtenues à partir de la méthode de l'opérateur invariant.

L'équation du mouvement pour l'amplitude dépendante du temps x pour un mode de flexion d'un nanotube de carbone en suspension de masse effective m est donné par [1]

$$ \ddot{x}+\left(\frac{\omega_{0}}{Q} +\eta x^{2}\right) \dot{x}+\left(\omega_{0}^{ 2}+\beta x^{2}\right) x =f_{\mathrm{d}}\cos (\omega t), $$ (1)

où ω ₀ est la fréquence angulaire de résonance, Q le facteur de qualité, f _d la force motrice électrostatique divisée par m , η le coefficient d'amortissement non linéaire, et β le paramètre Duffing. Supposons par commodité que le déplacement de la pointe est suffisamment petit par rapport à la longueur du fil CNT. Ensuite, nous pouvons négliger les termes non linéaires dans l'équation. (1), menant à [2]

$$ \ddot{x}+\frac{\omega_{0}}{Q} \dot{x}+\omega_{0}^{2} x =f_{\mathrm{d}}\cos (\omega t). $$ (2)

L'hamiltonien du système qui donne l'équation. (2) est donné par

$$ \hat{H}=e^{-\gamma t} \frac{\hat{p}^{2}}{2m} +\frac{1}{2}moi^{\gamma t} \left [\omega_{0}^{2} \hat{x}^{2} - 2f_{\mathrm{d}}\cos (\omega t)\hat{x}\right], $$ (3)

où γ =ω ₀ /Q . La solution classique de l'équation. (2) est composé d'une fonction complémentaire X _c (t ) et une solution particulière X _p (t ), qui sont donnés par

$$\begin{array}{@{}rcl@{}} &&X_{c}(t)=X_{c,0}e^{-\gamma t/2}\cos(\Omega t+\varphi) , \end{array} $$ (4) $$\begin{array}{@{}rcl@{}} &&X_{p}(t) =X_{p,0}\cos (\omega t - \ delta), \end{tableau} $$ (5)

où X _{c ,0} est une constante, $\Omega =\sqrt {\omega _{0}^{2} - \gamma ^{2}/4}$, φ est une phase arbitraire, et

$$\begin{array}{@{}rcl@{}} X_{p,0}&=&\frac{f_{\mathrm{d}}}{\sqrt{\left(\omega_{0}^ {2} -\omega^{2}\right)^{2} + \gamma^{2} \omega^{2}}}, \end{array} $$ (6) $$\begin{array} {@{}rcl@{}} \delta &=&\tan^{-1} \frac{\gamma \omega}{ \omega_{0}^{2} -\omega^{2}}. \end{tableau} $$ (7)

La solution classique dans l'espace des impulsions est donnée de manière similaire, où la fonction complémentaire est $P_{c} (t) =me^{\gamma t} \dot {X}_{c}(t)$ et la solution particulière est $P_{p} (t) =me^{\gamma t} \dot {X}_{p}(t)$. Pour étudier la phase géométrique du système, nous devons d'abord dériver des solutions quantiques. Notez que l'hamiltonien du système donné dans l'équation. (3) dépend explicitement du temps. Afin de dériver des solutions quantiques du système, nous utilisons la méthode de l'opérateur invariant [30, 31], qui est une méthode utile lorsque nous traitons un tel système variant dans le temps. Un opérateur invariant $\hat {I}$ du système peut être dérivé de l'équation de Liouville-von Neumann, qui est donnée par ${d \hat {I}}/{dt} ={\partial \hat {I}}/{\partial t} + \left [\hat {I},\hat {H}\right ]/\left (i\hbar \right) =0$. Par conséquent, à partir d'une évaluation rigoureuse après avoir inséré l'Eq. (3) dans cette équation, nous avons un opérateur invariant linéaire [34] de la forme

$$ \hat{I} =\hat{A} e^{i\Omega t}, $$ (8)

où $\hat {A}$ est l'opérateur d'annihilation qui est donné par

$$ \begin{aligned} \hat{A} =&\left(2\hbar m\Omega\right)^{-1/2} \left[ m \left(\Omega+ i\frac{\gamma}{ 2} \right) e^{\gamma t/2}\left[\hat{x}-X_{p}(t)\right]\right.\\ &\left.+ie^{-\gamma t /2} \gauche[\hat{p}-P_{p}(t)\right]\! {\vphantom{\left(\Omega+ i\frac{\gamma}{2} \right)}}\right]. \end{aligné} $$ (9)

L'adjoint hermitien de l'équation. (9), $\hat {A}^{\dagger }$, est l'opérateur de création.

Nous pouvons exprimer l'équation aux valeurs propres de $\hat {A}$ comme

$$ \hat{A} |A \rangle =A |A \rangle. $$ (10)

En évaluant l'équation ci-dessus, nous avons l'expression de la valeur propre telle que

$$ A(t) =A(0) e^{-i\Omega t}, $$ (11)

où A (0)=A ₀ e ^{−i φ} avec

$$ A_{0} =\left[m\Omega/(2\hbar)\right]^{1/2}X_{c,0}. $$ (12)

Tandis que l'état cohérent |A 〉 est l'état propre de $\hat {A}$, l'état compressé est l'état propre d'un opérateur $\hat {B}$ qui est donné par

$$ \hat{B} =\mu \hat{A} + \nu \hat{A}^{\dagger}, $$ (13)

où μ et ν sont des variables complexes qui donnent l'équation

$$ |\mu|^{2} - |\nu|^{2} =1. $$ (14)

Si on écrit l'équation aux valeurs propres de $\hat {B}$ sous la forme

$$ \hat{B} |B \rangle =B |B \rangle, $$ (15)

|B est l'état comprimé. En résolvant cette équation dans l'espace de configuration, on a

$$ {\begin{aligned} \langle {x}|B\rangle =&^{4}\!\!\!\sqrt{\frac{m \Omega e^{\gamma t}}{\hbar\ pi(\mu-\nu)(\mu^{*}-\nu^{*})}} \exp \left\{- \frac{1}{\hbar (\mu-\nu)} \left [\frac{1}{2} moi^{\gamma t}\left({\vphantom{\frac{1}{2}}}(\mu+\nu)\Omega \right.\right.\right. \\ &\left. +\frac{i\gamma}{2}(\mu-\nu)\right)\left[x-X_{p}(t)\right]^{2} -[iP_{ p}(t)(\mu-\nu)+ \left(2\hbar m \Omega e^{\gamma t}\right)^{1/2} \\ &\left. \left.\times(\mu A+\nu A^{*}) ]\left[x-X_{p}(t)\right] {\vphantom{\frac{1}{2} moi^{\gamma t}}}\right]-\frac{|A|^{2}+A^{2}}{2(\mu-\nu)(\mu^{*}-\nu^{*})} \à droite\}. \end{aligné}} $$ (16)

Ainsi, la fonction d'onde dans l'état comprimé a été dérivée comme indiqué dans l'équation. (16). Les caractéristiques quantiques du système peuvent être clarifiées sur la base d'une telle description analytique de la fonction d'onde. Pour μ =1 et ν =0, Éq. (16) se réduit à la fonction d'onde dans l'état cohérent, qui est l'état propre de l'Eq. (10) dans l'espace de configuration. La fonction d'onde, Eq. (16), sera utilisé dans la section suivante afin de dériver la phase géométrique dans l'état comprimé.

Résultats et discussion

Il est bien connu que la phase dans l'évolution des ondes quantiques implique la phase géométrique ainsi que la phase dynamique. La phase géométrique a été découverte pour la première fois par Berry en 1984 [12] pour un système évoluant cycliquement avec un changement adiabatique. D'après le théorème adiabatique de la mécanique quantique, un état propre instantané d'un état quantique en évolution cyclique dans l'espace des paramètres restera sur le même état plus tard, tandis qu'il y a une accumulation supplémentaire de la phase quantique qui est la phase de Berry. Une généralisation de la phase de Berry d'une manière qui inclut l'évolution non adiabatique, non cyclique et/ou non unitaire du système quantique est la phase géométrique.

La phase géométrique à l'état comprimé est donnée par

$$ \gamma_{G}(t) =\int_{0}^{t} \langle B(t') |i\frac{\partial}{\partial t'}| B(t') \rangle dt' +\gamma_{G}(0). $$ (17)

La différentiation de la fonction d'onde par rapport au temps dans l'espace de configuration devient

$$ \frac{\partial \langle {x}|B\rangle}{\partial t} \,=\, \left\{ f_{1}(t) \!\left[x-X_{p}( t)\right]^{2}\,+\,f_{2}(t) \left[x\,-\,X_{p}(t)\right]\,+\,f_{3}( t) \droit\}\! \!\langle {x}|B\rangle, $$ (18)

où

$$ f_{1}(t) =- \frac{m\gamma e^{\gamma t}}{2\hbar (\mu-\nu)} \left((\mu+\nu)\Omega + \ frac{i\gamma}{2}(\mu-\nu) \right), $$ (19) $$ {\begin{aligned} f_{2}(t) &=\frac{1}{\hbar (\mu-\nu)}\left[ \left((\mu+\nu)\Omega + \frac{i\gamma}{2}(\mu-\nu) \right) P_{p}(t) -ime^{\gamma t} \right.\\ &\quad\times\left[\omega_{0}^{2} X_{p}(t) - f_{\mathrm{d}} \cos(\ omega t)\right](\mu-\nu) +\left(2\hbar m \Omega e^{\gamma t}\right)^{1/2} \\ &\quad \left.\times\ left(\frac{\gamma}{2}\left(\mu A + \nu A^{*}\right)-i\Omega \left(\mu A - \nu A^{*}\right) \ right) \right], \\ \end{aligned}} $$ (20) $$ {\begin{aligned} f_{3}(t) &\!=\frac{\gamma}{4}-\frac {1}{\hbar me^{\gamma t}(\mu-\nu)} \left[iP_{p}(t)(\mu-\nu) + \left(2\hbar m\Omega e^ {\gamma t}\right)^{1/2} \right.\\ &\quad\left.\times\left(\mu A+\nu A^{*}\right){\vphantom{\left( 2\hbar m\Omega e^{\gamma t}\right)^{1/2}}}\right] P_{p}(t)+ \frac{i\Omega A^{2}}{(\ mu-\nu)\left(\mu^{*}-\nu^{*}\right)}. \end{aligné}} $$ (21)

Une évaluation plus poussée après l'insertion de l'Eq. (18) dans l'Éq. (17) donne

$$ {\begin{aligned} \gamma_{G}(t) =&\int_{0}^{t} dt' \left[ A_{0}^{2}\left(\frac{\gamma^{ 2}}{4\Omega}+\Omega + g_{1} \sin\left[2\left(\Omega t'+\varphi\right)\right] +g_{2} \cos\left[2\ left(\Omega t'+\varphi\right)\right] \right) \right.\\ &\left.-A_{0}\left[ g_{3}(t') \sin\left(\Omega t'+\varphi\right) +g_{4}(t') \cos\left(\Omega t'+\varphi\right) \right]+ g_{5}(t') {\vphantom{\frac {\gamma^{2}}{4\Omega}}}\right] +\gamma_{G}(0), \end{aligned}} $$ (22)

où

$$\begin{array}{*{20}l} g_{1}~ &=\frac{\gamma}{2} + \frac{i\Omega \left(\mu\nu^{*}-\ mu^{*}\nu\right)}{(\mu-\nu)\left(\mu^{*}-\nu^{*}\right)}, \end{array} $$ (23) $$\begin{array}{*{20}l} g_{2}~ &=\frac{\gamma^{2}}{4\Omega}+\Omega\frac{2|\nu|^{2 }- \left(\mu\nu^{*}+\mu^{*}\nu\right)}{(\mu-\nu) \left(\mu^{*}-\nu^{*} \right)}, \end{array} $$ (24) $$\begin{array}{*{20}l} g_{3}(t) &=\left(\frac{2\Omega}{m \hbar e^{\gamma t}} \right)^{1/2}P_{p}(t), \end{array} $$ (25) $$ {\begin{aligned} g_{4}( t) =\frac{1}{\sqrt{2\hbar\Omega}}\left(\frac{\gamma }{\sqrt{me^{\gamma t}}}P_{p}(t) - 2 \sqrt{me^{\gamma t}}\left[\omega_{0}^{2} X_{p}(t) - f_{\mathrm{d}} \cos(\omega t)\right]\ à droite), \end{aligned}} $$ (26) $$ {\begin{aligned} g_{5}(t) &=\frac{P_{p}^{2}(t)}{\hbar me ^{\gamma t}}+\frac{\gamma^{2}}{8\Omega}\left[2|\nu|^{2}-\left(\mu\nu+\mu^{*}\ nu^{*}\right) +1\right] \\ &\quad +\frac{i\gamma}{4(\mu-\nu)\left(\mu^{*}-\nu^{* }\right)} \left[|\mu|^{2}\left(\nu^{2}-\nu^{*2}\right)-|\nu|^{2}\lef t(\mu^{2}-\mu^{*2}\right)\right.\\ &\quad\left.+ (2|\nu|^{2}+1)\left(\mu\ nu^{*}-\mu^{*}\nu\right) +(\mu-\mu^{*})(\nu-\nu^{*})\right]. \end{aligné}} $$ (27)

Le dernier terme de g ₅ qui contient (μ −μ ^∗ )(ν −ν ^∗ ) est inadéquat comme phase car il s'agit d'un nombre purement imaginaire. Par conséquent, nous supprimons maintenant ce terme en choisissant au moins l'un des μ et ν comme une valeur réelle. Ce remède peut toujours être fait sans perte de généralité, car seule la phase relative entre μ et ν a une signification physique plutôt que leurs phases absolues.

A partir de l'exécution de l'intégration dans l'Eq. (22), nous avons

$$ {\begin{aligned} \gamma_{G}(t) &=A_{0}^{2}\left[\left(\frac{\gamma^{2}}{4\Omega}+\Omega \right)t + \frac{g_{1}}{\Omega}\sin(\Omega t+2\varphi) \sin(\Omega t) +\frac{g_{2}}{\Omega} \cos (\Omega t+2\varphi) \right.\\ &\quad\left.\times\sin(\Omega t) {\vphantom{\frac{\gamma^{2}}{4\Omega}}} \right]\!-A_{0}\left[ \left(\frac{2m\Omega}{\hbar} \right)^{1/2}\omega X_{p,0} \bar{g}_ {3}(t) +\sqrt{\frac{2m}{\hbar\Omega}}\frac{1}{4\omega^{2}+\gamma^{2}}\bar{g}_{ 4}(t) \right]\\ &\quad+ \bar{g}_{5}(t) +\gamma_{G}(0), \end{aligned}} $$ (28)

où $\bar {g}_{i}(t)~(i=3,4,5)$ sont donnés par

$$ \bar{g}_{i}(t) =G_{i}(t) -G_{i}(0), $$ (29)

avec

$$ {\begin{aligned} G_{3}(\tau) &=e^{\gamma \tau/2}\left(\frac{1}{4(\Omega+\omega)^{2}+\ gamma^{2}} \left\{2(\Omega+\omega)\sin[(\Omega+\omega)\tau+\varphi-\delta] \right.\right.\\ &\quad\left.+\ gamma \cos[(\Omega+\omega)\tau+\varphi-\delta] \right\}- \frac{1}{4(\Omega-\omega)^{2}+\gamma^{2}} \ { 2(\Omega-\omega) \\ &\quad\left.\left.\times\sin[(\Omega-\omega)\tau\,+\,\varphi\,+\,\delta]\ !+\gamma \cos[(\Omega-\omega)\tau\,+\,\varphi\,+\,\delta]\right\} {\vphantom{\frac{1}{4(\Omega+\ omega)^{2}+\gamma^{2}}}}\right),\\ \end{aligned}} $$ (30) $$ {\begin{aligned} G_{4}(\tau) &=e^{\gamma \tau/2} \left\{X_{p,0} \left\{ \gamma\omega[ 2\omega\cos(\omega \tau-\delta)-\gamma \sin( \omega \tau-\delta)] -2\omega_{0}^{2} \right.\right.\\ &\quad\left.\times[2\omega\sin(\omega \tau-\delta )+\gamma \cos(\omega \tau-\delta)] {\vphantom{X_{p,0}}}\right\}+2f_{\mathrm{d}} [ 2\omega\sin(\omega \tau) \\ &\left.\left.\quad+\gamma \cos(\omega \tau)\right]{\vphantom{X_{p,0}}}\right\}, \\ \end{aligné }} $$ ( 31) $$ {\begin{aligned} G_{5}(\tau) &=\frac{m\omega^{2}}{2\hbar}X_{p,0}^{2} \frac{e ^{\gamma \tau}}{\gamma \left(4\omega^{2}+\gamma^{2}\right)} \left\{ \gamma^{2}+4\omega^{2} -\gamma^{2} \cos[2(\omega\tau -\delta)]\right.\\ &\quad\left.-2\gamma\omega \sin[2(\omega \tau -\delta )] {\vphantom{\gamma^{2}+4\omega^{2} -\gamma^{2}}}\right\} +\frac{\gamma^{2} \tau}{8\Omega }\left[2|\nu|^{2}-\left(\mu\nu+\mu^{*}\nu^{*}\right)+1\right] \\ &\quad+\frac{i \gamma \tau}{4(\mu-\nu)\left(\mu^{*}-\nu^{*}\right)} \left[|\mu|^{2}\left(\nu ^{2}-\nu^{*2}\right)-|\nu|^{2}\left(\mu^{2}-\mu^{*2}\right)\right.\\ &\quad\left.+\left(2|\nu|^{2}+1\right)\left(\mu\nu^{*}-\mu^{*}\nu\right)\right]. \end{aligné}} $$ (32)

Ainsi, nous avons évalué la phase géométrique complète dans l'état comprimé, qui est donnée par l'équation. (28) avec les équations. (23), (24) et (29)–(32).

L'évolution temporelle de la phase géométrique a été illustrée sur les Fig. 1, 2, 3 et 4. À partir de la figure 1, nous voyons que la phase géométrique oscille et que l'enveloppe d'une telle oscillation augmente avec le temps. L'augmentation de l'enveloppe est plus importante lorsque A ₀ est large. Le modèle de l'oscillation devient progressivement irrégulier à mesure que les valeurs de μ et ν augmenter. De plus, l'amplitude de l'oscillation devient grande avec le temps.

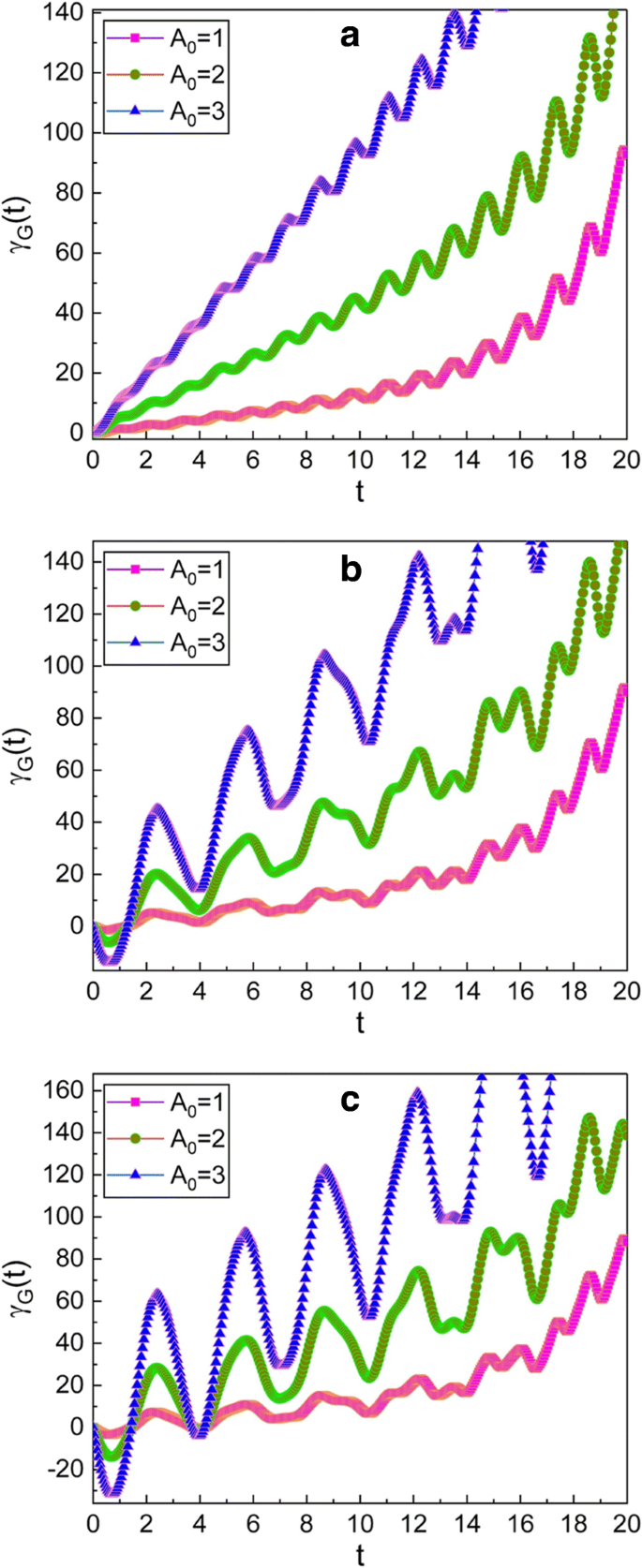
Evolution temporelle de la phase géométrique pour plusieurs valeurs différentes de A ₀ . Les valeurs de (μ , ν ) utilisés dans les graphiques sont (1, 0) pour a , ($\sqrt {2}$, 1) pour b , et ($\sqrt {3}$, $\sqrt {2}$) pour c . Nous avons utilisé m =1, ω ₀ =1, ω =5, γ =0.35, f _d =1, $\hbar =1$, φ =0, et γ _G (0)=0. La phase et tous les paramètres sont considérés comme sans dimension pour plus de commodité, et cette convention sera également appliquée aux figures suivantes. Parce que A ₀ est donnée en fonction de l'amplitude classique X _{c ,0} de la fonction complémentaire [voir Eq. (12)], nous pouvons confirmer à partir des graphiques que la phase géométrique est grande lorsque l'amplitude d'oscillation est élevée. On voit aussi que la fluctuation de γ _G (t ) devient grand lorsque les valeurs μ et ν augmenter sous la condition donnée dans l'équation. (14)

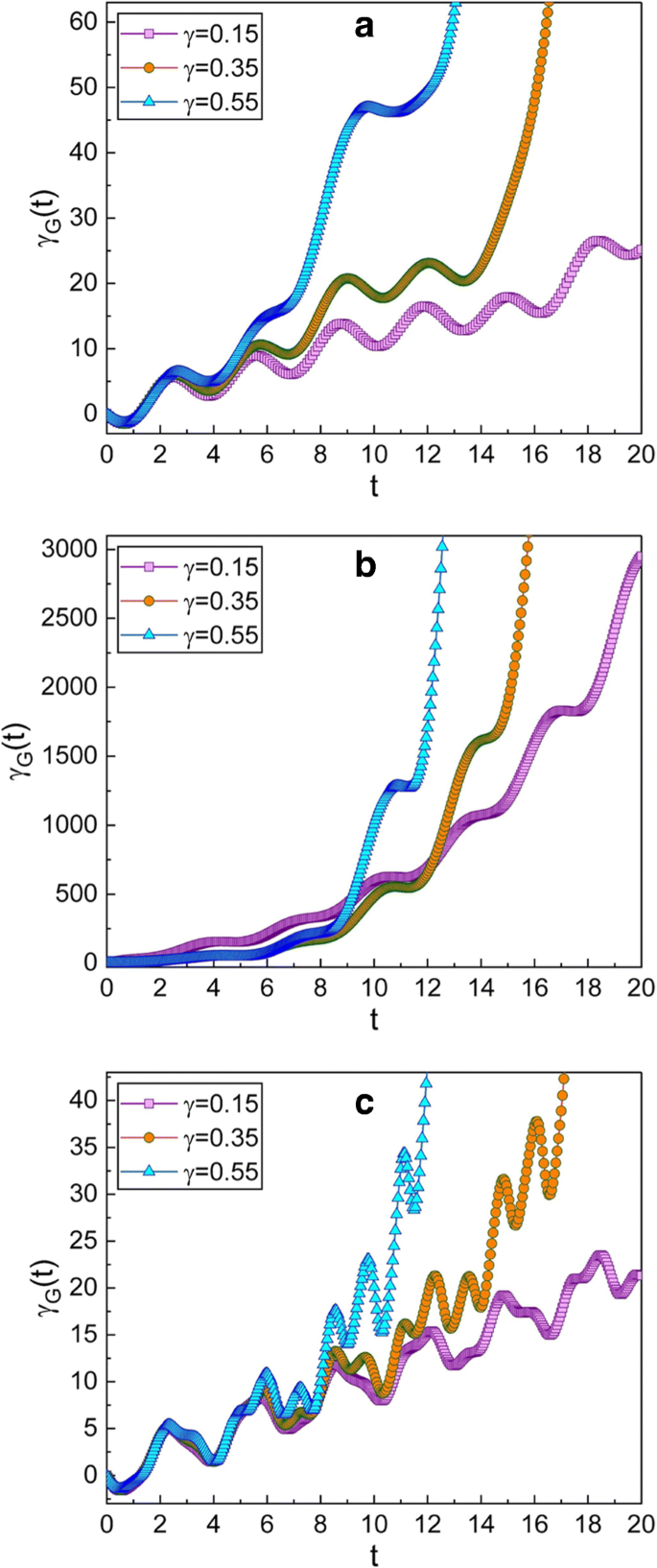
Evolution temporelle de la phase géométrique pour plusieurs valeurs différentes de γ . La valeur de ω utilisé dans les graphiques est 0.3 pour a , 0.99 pour b , et 5 pour c . Les paramètres de compression choisis ici sont $\mu =\sqrt {2}$ et ν =1 ; ce choix donne q -état comprimé au moment initial. Les autres quantités que nous avons utilisées sont m =1, ω ₀ =1, A ₀ =1, f _d =1, $\hbar =1$, φ =0, et γ _G (0)=0. Nous confirmons que la phase géométrique est grande lorsque le facteur d'amortissement γ est grand dans la plupart des cas, mais pas tous. La fréquence du cas b est proche de la fréquence de résonance, alors que celles de a et c sont loin de la résonance. La phase géométrique pour le cas résonant (b ) augmente très rapidement dans le temps

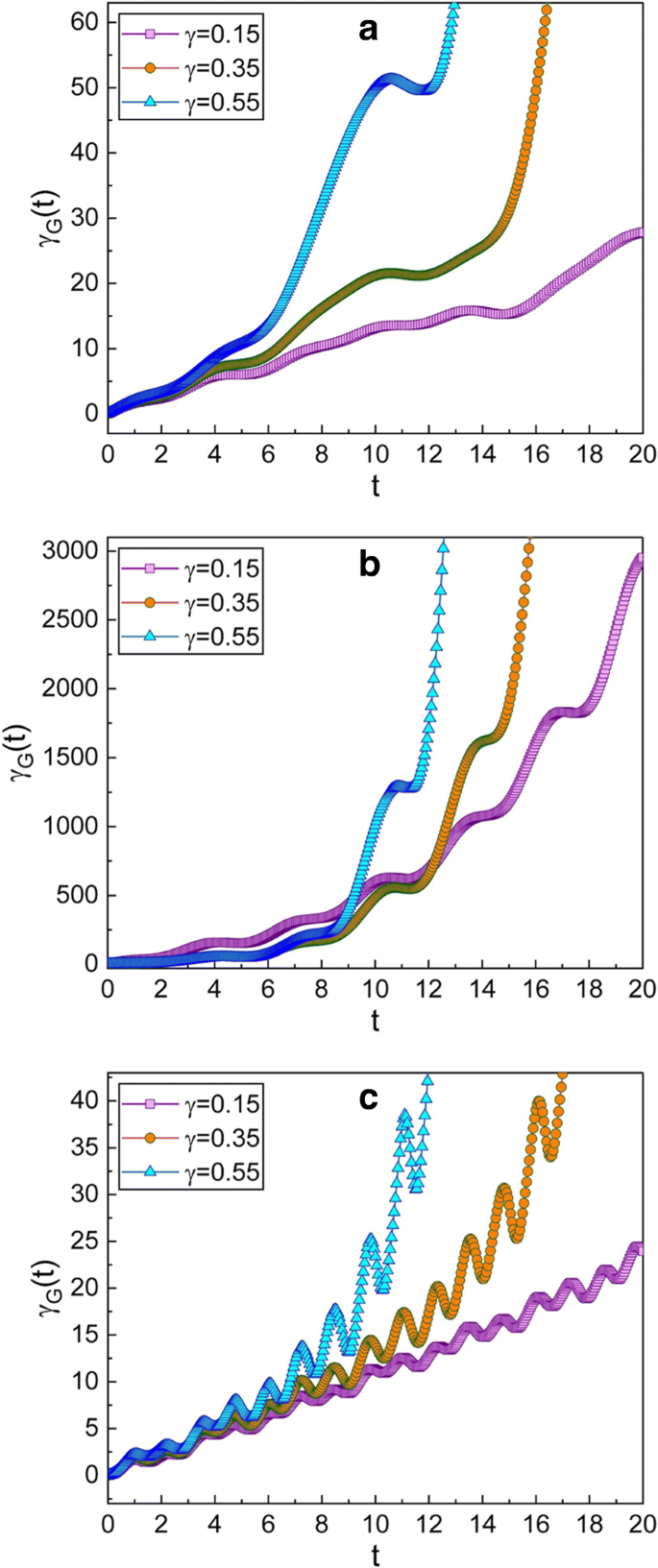
un –c Ce graphique est le même que la Fig. 2, mais pour le cas où les paramètres de compression choisis sont $\mu =\sqrt {2}$ et ν =−1 qui donne un p -état comprimé au moment initial. Du fait que les graphiques globaux dans ce cas ne sont pas tellement différents de ceux correspondants de la Fig. 2, nous pouvons confirmer que l'évolution de γ _G (t ) est presque sans rapport avec les types de compression tant que les valeurs absolues de μ et ν ne change pas

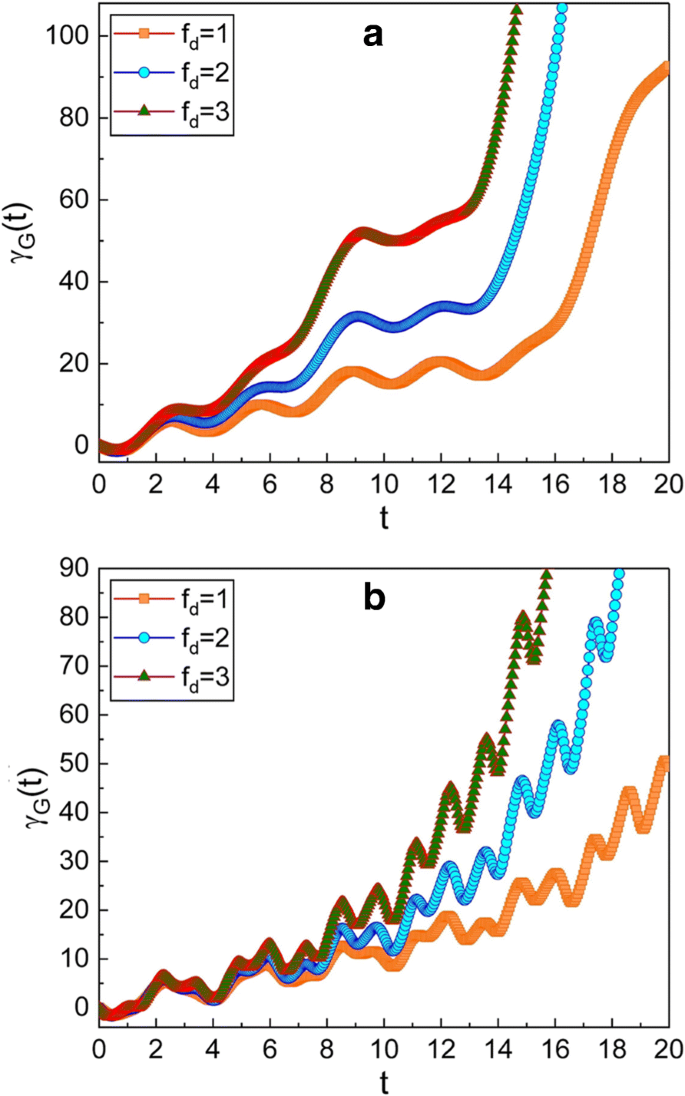
Evolution temporelle de la phase géométrique pour plusieurs valeurs différentes de f _d . La valeur de ω utilisé dans les graphiques est 0.3 pour a et 5 pour b . Nous avons utilisé $\mu =\sqrt {2}$, ν =1, m =1, ω ₀ =1, γ =0.3, A ₀ =1, $\hbar =1$, φ =0, et γ _G (0)=0. Comme l'amplitude (f _d ) de la force motrice augmente, la phase géométrique devient grande

Les effets de compression à l'état comprimé en fonction du paramètre de compression c où c =μ /ν a été étudié dans la réf. [39]. D'après l'analyse donnée dans la réf. [39] (voir Fig. 1(a) dans la réf. [39]), l'état comprimé illustré dans la Fig. 2, qui correspond à $c=\sqrt {2}$, est le q -état comprimé au temps initial, tandis que celui de la figure 3, qui correspond à $c=-\sqrt {2}$, est le p -état comprimé dans la même situation. En comparant les Fig. 2 et 3 entre eux, nous pouvons conclure que la phase géométrique dans le q -l'état compressé est presque le même que celui dans le p -état comprimé.

Les effets de γ sur l'évolution de la phase géométrique peut être confirmé à partir des Figs. 2 et 3. La phase géométrique augmente plus rapidement lorsque γ est large. En comparant les Fig. 2a et 3a avec les Figs. 2c et 3c, nous pouvons confirmer que la phase géométrique varie assez rapidement lorsque ω est supérieure à la fréquence angulaire de résonance.

Le comportement temporel de la phase géométrique à ou près de l'état de résonance du système peut être d'un grand intérêt [22, 23]. Les figures 2b et 3b montrent que la phase géométrique augmente très rapidement lorsque ω est proche de la fréquence angulaire de résonance. Cela signifie que la fonction d'onde dans cette situation varie considérablement dans le temps, car l'amplitude de la phase géométrique est liée à la variation temporelle de la fonction d'onde. En effet, l'amplitude de l'oscillation du fil est remarquablement augmentée à l'état de résonance. Soit dit en passant, les fréquences angulaires de résonance des résonateurs à nanofils suspendus à base de CNT sont non seulement élevées, mais également largement accordables avec des facteurs de très haute qualité [3]. Pour cette raison, les modes vibrationnels du système seront conservés pendant longtemps jusqu'à ce qu'ils soient complètement amortis [11].

La figure 4 montre que la phase géométrique est également affectée par l'amplitude de la force motrice f _d . Comme f _d augmente, l'incrément de la phase géométrique dans le temps est rapide.

Conclusion

Nous avons étudié la phase géométrique à l'état comprimé du système sur la base de la dynamique quantique avec l'équation de Schrödinger. Concernant la dépendance temporelle de l'hamiltonien qui décrit le système, la méthode de l'opérateur invariant a été introduite, qui est un outil potentiel pour dériver des solutions quantiques dans le cas où l'hamiltonien est décrit en termes de temps. Grâce à cette méthode, la formule analytique de la phase géométrique pour l'oscillation des nanofils à base de CNT a été obtenue.

Une analyse détaillée des effets de phase, nécessaire à la compréhension théorique des vibrations mécaniques, a été réalisée. Notre développement de la phase géométrique est entièrement quantique avec des évaluations mathématiques rigoureuses. La phase géométrique est sensible au changement des paramètres mécaniques et présente une oscillation dans un grand nombre de cas. L'influence des paramètres de compression sur l'évolution de la phase géométrique a également été analysée. Nous avons confirmé une forte augmentation de l'accumulation de phase géométrique au cours du temps près de la fréquence angulaire de résonance.

Nos résultats illustrent le comportement temporel de la phase géométrique qui apparaît dans la vibration d'un nanofil à base de CNT. L'analyse de la phase géométrique donnée dans ce travail est importante pour comprendre non seulement les caractéristiques topologiques du système, mais également les vibrations dynamiques d'autres oscillateurs mécaniques à base de nanofils. En particulier, nous avons développé des propriétés de phase de l'état de résonance, dont une clarification est nécessaire dans l'application du système dans les technologies de l'information quantique et d'autres industries quantiques [40]. La méthode et le cadre similaires utilisés dans cette recherche peuvent également être étendus à d'autres nanosystèmes, tels que les résonateurs supraconducteurs Fabry-Perot [41], les nano cantilevers [42] et les systèmes hybrides qubit-résonateur-atome [43].

Abréviations

CNT :: Nanotube de carbone
Ondes EM :: Ondes électromagnétiques
TDHS :: Système hamiltonien dépendant du temps

Croissance directe de nanofils de GaN monocristallin sur de la silice recouverte d'oxyde d'indium FET à canal U rectangulaire hautes performances avec une distance de seulement 2 nm entre les contacts source et drain

Nanomatériaux