Machine à états finis
La rétroaction est un principe d'ingénierie fascinant. Il peut transformer un appareil ou un processus plutôt simple en quelque chose de beaucoup plus complexe. Nous avons vu les effets de la rétroaction intentionnellement intégrés dans les conceptions de circuits avec des effets plutôt étonnants :
- Comparateur + rétroaction négative—————-> amplificateur à gain contrôlable
- Comparateur + retour positif—————-> comparateur avec hystérésis
- Logique combinatoire + retour positif—> multivibrateur
Dans le domaine de l'instrumentation des procédés, le retour d'expérience est utilisé pour transformer un simple système de mesure en quelque chose de contrôlable :
- Système de mesure + rétroaction négative --> système de contrôle en boucle fermée
La rétroaction, à la fois positive et négative, a tendance à ajouter une toute nouvelle dynamique au fonctionnement d'un appareil ou d'un système. Parfois, ces nouvelles dynamiques trouvent une application utile, tandis que d'autres fois elles sont simplement intéressantes.
Avec des tables de consultation programmées dans des dispositifs de mémoire, le retour des sorties de données vers les entrées d'adresse crée un tout nouveau type de dispositif :la machine à états finis , ou FSM :
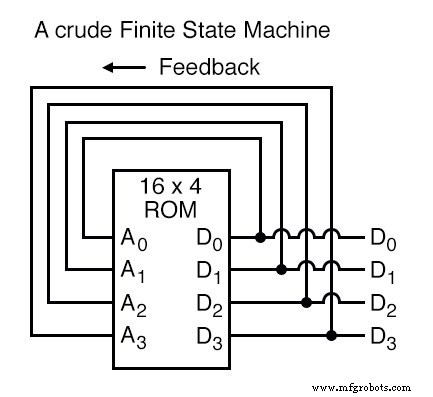
Le circuit ci-dessus illustre l'idée de base :les données stockées à chaque adresse deviennent le prochain emplacement de stockage auquel la ROM est adressée. Le résultat est une séquence spécifique de nombres binaires (suivant la séquence programmée dans la ROM) à la sortie, au fil du temps.
Pour éviter les problèmes de synchronisation du signal, cependant, nous devons reconnecter les sorties de données aux entrées d'adresse via une bascule de type D à 4 bits, de sorte que la séquence se déroule pas à pas au rythme d'une impulsion d'horloge contrôlée :
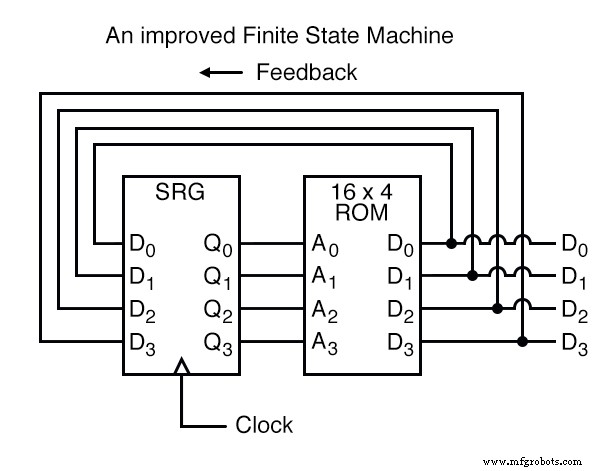
Une analogie pour le fonctionnement d'un tel appareil pourrait être un ensemble de boîtes postales, chacune avec un numéro d'identification sur la porte (l'adresse), et chacune contenant un morceau de papier avec l'adresse d'un autre P.O. case écrite dessus (les données). Une personne, ouvrant le premier P.O. case, y trouverait l'adresse du prochain B.P. boîte à ouvrir.
En stockant un modèle particulier d'adresses dans le P.O. boîtes, nous pouvons dicter l'ordre dans lequel chaque boîte est ouverte, et donc l'ordre dans lequel le papier est lu.
Ayant 16 emplacements de mémoire adressables dans la ROM, cette machine à états finis aurait 16 « états » stables différents dans lesquels elle pourrait se verrouiller. Dans chacun de ces états, l'identité de l'état suivant serait programmée dans la ROM, en attendant que le signal de la prochaine impulsion d'horloge soit renvoyé à la ROM en tant qu'adresse.
Une application utile d'un tel FSM serait de générer une séquence de comptage arbitraire, telle que le code Gray :
Adresse -----> Séquence de comptage du code Gray de données :0000 -------> 0001 0 0000 0001 -------> 0011 1 0001 0010 -------> 0110 2 0011 0011 -------> 0010 3 0010 0100 -------> 1100 4 0110 0101 -------> 0100 5 0111 0110 -------> 0111 6 0101 0111 -------> 0101 7 0100 1000 -------> 0000 8 1100 1001 -------> 1000 9 1101 1010 -------> 1011 10 1111 1011 -------> 1001 11 1110 1100 -------> 1101 12 1010 1101 -------> 1111 13 1011 1110 -------> 1010 14 1001 1111 -------> 1110 15 1000
Essayez de suivre la séquence de comptage du code Gray comme le ferait le FSM :à partir de 0000, suivez les données stockées à cette adresse (0001) jusqu'à l'adresse suivante, et ainsi de suite (0011), et ainsi de suite (0010), et ainsi de suite sur (0110), etc. Le résultat, pour la table de programme montrée, est que la séquence d'adressage saute d'adresse en adresse d'une manière qui semble aléatoire, mais lorsque vous vérifiez chaque adresse à laquelle vous accédez, vous constaterez que il suit l'ordre correct pour le code Gray à 4 bits.
Lorsque le FSM arrive à son dernier état programmé (adresse 1000), les données qui y sont stockées sont 0000, ce qui recommence toute la séquence à l'adresse 0000 au pas de la prochaine impulsion d'horloge.
Nous pourrions étendre les capacités du circuit ci-dessus en utilisant une ROM avec plus de lignes d'adresse et en ajoutant plus de données de programmation :
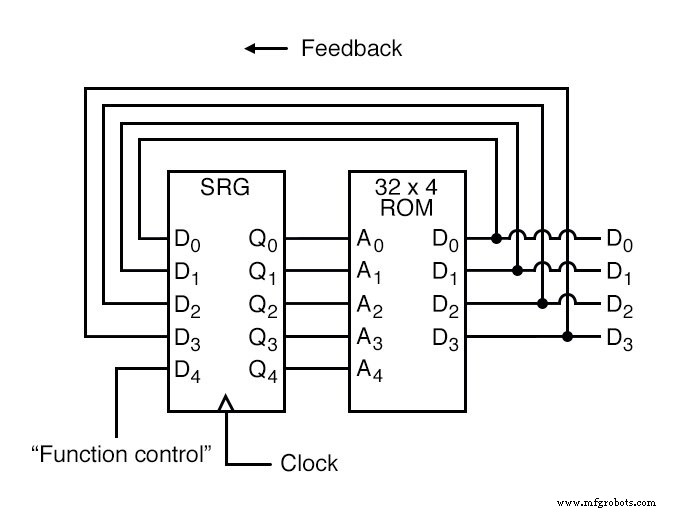
Maintenant, tout comme le circuit additionneur de table de consultation que nous avons transformé en unité logique arithmétique (+, -, x, / fonctions) en utilisant plus de lignes d'adresse comme entrées de « contrôle de fonction », ce compteur FSM peut être utilisé pour générer plus plus d'une séquence de comptage, une séquence différente programmée pour les quatre bits de retour (A0 à A3) pour chacune des deux combinaisons d'entrée de ligne de commande de fonction (A4 =0 ou 1).
Si A4 vaut 0, le FSM compte en binaire; si A4 vaut 1, le FSM compte en Gray Code. Dans les deux cas, la séquence de comptage est arbitraire :déterminée par le caprice du programmeur. D'ailleurs, la séquence de comptage n'a même pas besoin d'avoir 16 étapes, car le programmeur peut décider de faire recycler la séquence à 0000 à n'importe laquelle des étapes. C'est un dispositif de comptage complètement flexible, le comportement strictement déterminé par le logiciel (programmation) dans la ROM.
Nous pouvons étendre encore plus les capacités du FSM en utilisant une puce ROM avec des lignes d'entrée d'adresse et de sortie de données supplémentaires. Prenons par exemple le circuit suivant :
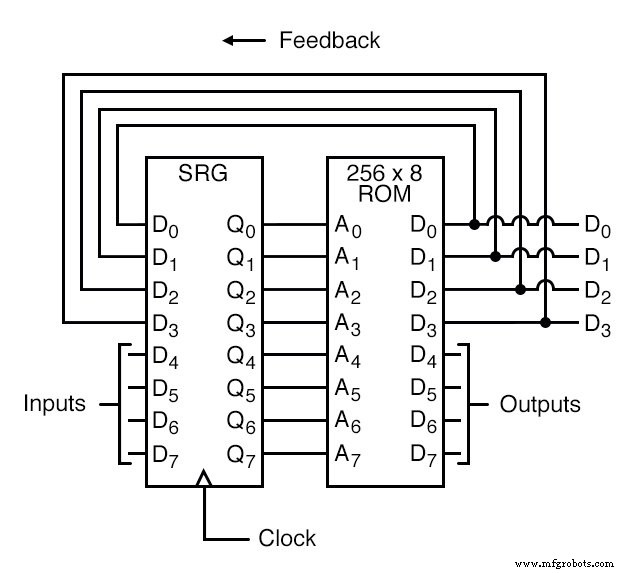
Ici, les sorties de données D0 à D3 sont utilisées exclusivement pour le retour vers les lignes d'adresse A0 à A3. Les lignes de sortie de date D4 à D7 peuvent être programmées pour sortir autre chose que la valeur « état » du FSM. Étant donné que quatre bits de sortie de données sont renvoyés à quatre bits d'adresse, il s'agit toujours d'un périphérique à 16 états.
Cependant, le fait que les données de sortie proviennent d'autres lignes de sortie de données donne au programmeur plus de liberté pour configurer les fonctions qu'auparavant. En d'autres termes, cet appareil peut faire bien plus que simplement compter ! La sortie programmée de ce FSM dépend non seulement de l'état des lignes d'adresse de retour (A0 à A3), mais aussi des états des lignes d'entrée (A4 à A7).
L'entrée du signal d'horloge de la bascule de type D ne doit pas non plus provenir d'un générateur d'impulsions. Pour rendre les choses plus intéressantes, la bascule peut être câblée pour synchroniser un événement externe, de sorte que le FSM passe à l'état suivant uniquement lorsqu'un signal d'entrée le lui demande.
Nous avons maintenant un appareil qui correspond mieux au sens du mot « programmable ». Les données écrites dans la ROM sont un programme dans le vrai sens du terme :les sorties suivent un ordre préétabli basé sur les entrées de l'appareil et sur quelle « étape » se trouve l'appareil dans sa séquence.
Ceci est très proche de la conception opérationnelle de la Machine de Turing , un dispositif informatique théorique inventé par Alan Turing, mathématiquement prouvé capable de résoudre n'importe quel problème arithmétique connu, avec une capacité de mémoire suffisante.
Technologie industrielle



