Tables de correspondance

Ayant appris les dispositifs de mémoire numérique dans le dernier chapitre, nous savons qu'il est possible de stocker des données binaires dans des dispositifs à semi-conducteurs. Ces « cellules » de stockage dans les dispositifs de mémoire à semi-conducteurs sont facilement adressées en pilotant les lignes « d'adresse » du dispositif avec la ou les valeurs binaires appropriées.

Supposons que nous ayons un circuit de mémoire ROM écrit ou programmé avec certaines données, de telle sorte que les lignes d'adresse de la ROM servent d'entrées et les lignes de données de la ROM servent de sorties, générant la réponse caractéristique d'une fonction logique particulière. Théoriquement, nous pourrions programmer cette puce ROM pour émuler la fonction logique que nous voulions sans avoir à modifier les connexions filaires ou les portes.

Considérons l'exemple suivant d'une mémoire ROM 4 x 2 bits (une très petite mémoire !) programmée avec la fonctionnalité d'un demi-additionneur :

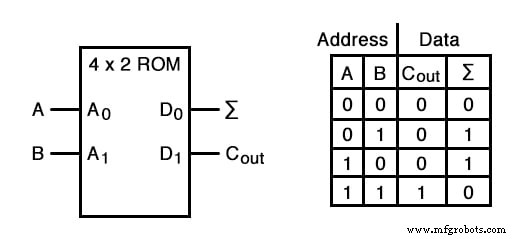
Si cette ROM a été écrite avec les données ci-dessus (représentant la table de vérité d'un demi-additionneur), le pilotage des entrées d'adresses A et B entraînera l'activation des cellules de mémoire respectives dans la puce ROM, produisant ainsi les données correspondantes sous la forme Σ ( Somme) et C_out morceaux. Contrairement au circuit de demi-additionneur composé de portes ou de relais, cet appareil peut être configuré pour exécuter n'importe quelle fonction logique avec deux entrées et deux sorties, pas seulement la fonction de demi-additionneur.

Pour changer la fonction logique, il nous suffirait d'écrire une table de données différente sur une autre puce ROM. Nous pourrions même utiliser une puce EPROM qui pourrait être réécrite à volonté, offrant une flexibilité de fonctionnement ultime.

Il est d'une importance vitale de reconnaître l'importance de ce principe appliqué aux circuits numériques. Alors que le demi-additionneur construit à partir de portes ou de relais processus les bits d'entrée pour arriver à une sortie spécifique, la ROM se se souvient simplement quelles devraient être les sorties pour une combinaison donnée d'entrées.

Ce n'est pas très différent des « tables de multiplication » mémorisées à l'école primaire :plutôt que d'avoir à calculer le produit de 5 fois 6 (5 + 5 + 5 + 5 + 5 + 5 =30), les écoliers apprennent à se souvenir que 5 x 6 =30, puis s'attend à rappeler ce produit de la mémoire au besoin. De même, plutôt que la fonction logique dépendant de l'agencement fonctionnel des portes ou relais filaires (hardware), elle dépend uniquement des données écrites dans la mémoire (software).

Une application aussi simple, avec des sorties définies pour chaque entrée, s'appelle une table de consultation , parce que le périphérique de mémoire « recherche » simplement ce que la ou les sorties devraient être pour une combinaison donnée d'états d'entrée.

Cette application d'un dispositif de mémoire pour exécuter des fonctions logiques est importante pour plusieurs raisons :

• Le logiciel est beaucoup plus facile à changer que le matériel.
• Le logiciel peut être archivé sur différents types de supports mémoire (disque, bande), offrant ainsi un moyen simple de documenter et de manipuler la fonction sous une forme « virtuelle » ; le matériel ne peut être « archivé » que de manière abstraite sous la forme d'une sorte de dessin graphique.
• Le logiciel peut être copié d'un périphérique de mémoire (tel que la puce EPROM) à un autre, permettant à un périphérique d'« apprendre » sa fonction à partir d'un autre périphérique.
• Un logiciel tel que l'exemple de fonction logique peut être conçu pour exécuter des fonctions qui seraient extrêmement difficiles à émuler avec des portes logiques discrètes (ou des relais !).

L'utilité d'une table de consultation devient de plus en plus évidente avec la complexité croissante de la fonction. Supposons que nous voulions construire un circuit additionneur de 4 bits à l'aide d'une ROM. Nous aurions besoin d'une ROM avec 8 lignes d'adresse (deux nombres de 4 bits à additionner), plus 4 lignes de données (pour la sortie signée) :

Avec 256 emplacements de mémoire adressables dans cette puce ROM, nous aurions une bonne quantité de programmation à faire, lui indiquant quelle sortie binaire générer pour chaque combinaison d'entrées binaires.

Nous courrions également le risque de faire une erreur dans notre programmation et de lui faire sortir une somme incorrecte, si nous ne faisions pas attention. Cependant, la flexibilité de pouvoir configurer cette fonction (ou n'importe quelle fonction) par le seul logiciel l'emporte généralement sur ces coûts.

Considérez certaines des fonctions avancées que nous pourrions implémenter avec l'« additionneur » ci-dessus. Nous savons que lorsque nous ajoutons deux ensembles de nombres en notation signée complément à 2, nous risquons de faire déborder la réponse.

Par exemple, si nous essayons d'ajouter 0111 (décimal 7) à 0110 (décimal 6) avec seulement un champ numérique de 4 bits, la réponse que nous obtiendrons est 1001 (décimal -7) au lieu de la valeur correcte, 13 (7 + 6), qui ne s'exprime pas à l'aide de 4 bits signés. Si nous le voulions, nous pourrions éviter les réponses étranges données dans les conditions de débordement en programmant ce circuit de table de consultation pour produire autre chose dans des conditions où nous savons qu'un débordement se produira (c'est-à-dire dans tous les cas où la somme réelle dépasserait +7 ou -8).

Une alternative pourrait être de programmer la ROM pour sortir la quantité 0111 (la valeur positive maximale qui peut être représentée avec 4 bits signés), ou toute autre valeur que nous avons déterminée comme étant plus appropriée pour l'application que la valeur "d'erreur" débordée typique qu'un circuit additionneur régulier produirait. C'est au programmeur de décider ce qu'il veut que ce circuit fasse, car nous ne sommes plus limités par les contraintes des fonctions des portes logiques.

Les possibilités ne s'arrêtent pas non plus aux fonctions logiques personnalisées. En ajoutant plus de lignes d'adresse à la puce ROM 256 x 4, nous pouvons étendre la table de recherche pour inclure plusieurs fonctions :

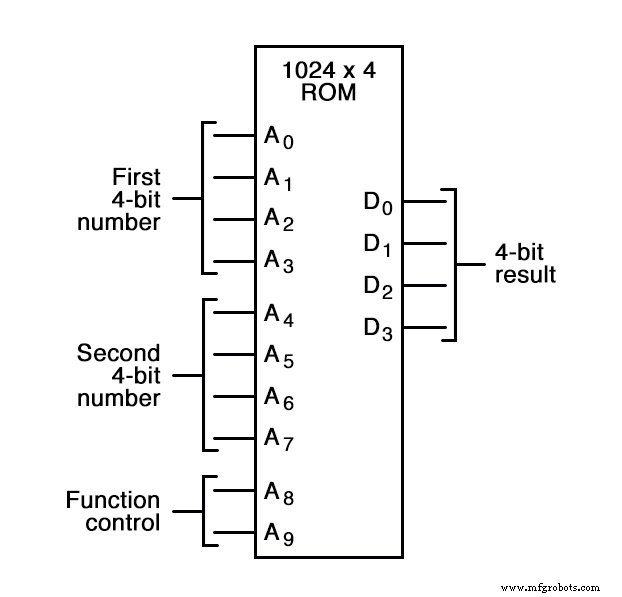
Avec deux lignes d'adresses supplémentaires, la puce ROM aura 4 fois plus d'adresses qu'avant (1024 au lieu de 256). Cette ROM pourrait être programmée de sorte que lorsque A8 et A9 étaient tous les deux bas, les données de sortie représentaient la somme des deux nombres binaires à 4 bits entrés sur les lignes d'adresse A0 à A7, tout comme nous l'avions avec le précédent circuit ROM 256 x 4.

Pour les adresses A8=1 et A9=0, il peut être programmé pour sortir la différence (soustraction) entre le premier nombre binaire à 4 bits (A0 à A3) et le deuxième nombre binaire (A4 à A7). Pour les adresses A8=0 et A9=1, nous pourrions programmer la ROM pour sortir la différence (soustraction) des deux nombres dans l'ordre inverse (second - premier plutôt que premier - deuxième), et enfin, pour les adresses A8=1 et A9=1, la ROM peut être programmée pour comparer les deux entrées et fournir une indication d'égalité ou d'inégalité.

Ce que nous aurons alors est un appareil qui peut effectuer quatre opérations arithmétiques différentes sur des nombres binaires à 4 bits, le tout en « recherchant » les réponses qui y sont programmées.

Si nous avions utilisé une puce ROM avec plus de deux lignes d'adresse supplémentaires, nous pourrions la programmer avec une plus grande variété de fonctions à exécuter sur les deux entrées 4 bits. Il existe un certain nombre d'opérations propres aux données binaires (telles que le contrôle de parité ou le OU exclusif de bits) que nous pourrions trouver utile d'avoir programmées dans une telle table de consultation.

Des appareils tels que celui-ci, qui peuvent effectuer une variété de tâches arithmétiques dictées par un code d'entrée binaire, sont connus sous le nom d'Unités arithmétiques logiques (ALU), et ils constituent l'une des composantes essentielles de la technologie informatique. Bien que les ALU modernes soient plus souvent construites à partir de circuits logiques combinatoires (porte) très complexes pour des raisons de vitesse, il devrait être réconfortant de savoir que la même fonctionnalité exacte peut être dupliquée avec une puce ROM « muette » programmée avec la table de consultation appropriée (s).

En fait, cette approche exacte a été utilisée par les ingénieurs d'IBM en 1959 avec le développement des ordinateurs IBM 1401 et 1620, qui utilisaient des tables de consultation pour effectuer des additions, plutôt que des circuits d'addition binaire. La machine était affectueusement connue sous le nom de « CADET », qui signifiait « C pas A jj, D n'est pas E même T ry."

Une application très courante pour les ROM de table de consultation est dans les systèmes de contrôle où une fonction mathématique personnalisée doit être représentée. Une telle application se trouve dans les systèmes d'injection de carburant commandés par ordinateur pour les moteurs d'automobile, où le rapport de mélange air/carburant approprié pour un fonctionnement efficace et propre change avec plusieurs variables environnementales et opérationnelles.

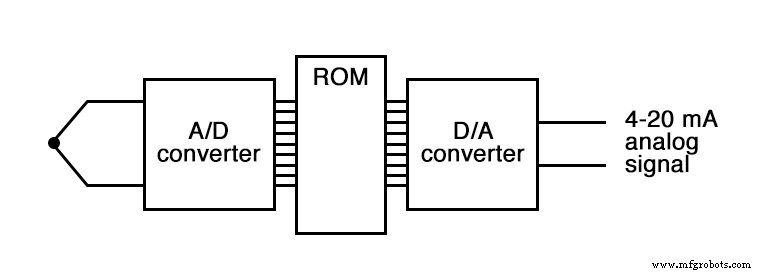
Les tests effectués sur les moteurs dans les laboratoires de recherche déterminent quels sont ces rapports idéaux pour diverses conditions de charge du moteur, de température de l'air ambiant et de pression atmosphérique barométrique. Les variables sont mesurées avec des transducteurs de capteur, leurs sorties analogiques converties en signaux numériques avec des circuits A/N, et ces signaux numériques parallèles utilisés comme entrées d'adresse vers une puce ROM haute capacité programmée pour produire la valeur numérique optimale pour le rapport air/carburant pour l'une de ces conditions données.

Parfois, les ROM sont utilisées pour fournir des fonctions de table de consultation unidimensionnelle, pour « corriger » les valeurs de signal numérisées afin qu'elles représentent plus précisément leur signification dans le monde réel. Un exemple d'un tel appareil est un émetteur de thermocouple , qui mesure le signal de millivoltage généré par une jonction de métaux différents et produit un signal qui est censé directement correspondent à cette température de jonction.

Malheureusement, les jonctions de thermocouple n'ont pas de réponses température/tension parfaitement linéaires, et donc le signal de tension brut n'est pas parfaitement proportionnel à la température. En numérisant le signal de tension (conversion A/N) et en envoyant cette valeur numérique à l'adresse d'une ROM programmée avec les valeurs de correction nécessaires, la programmation de la ROM pourrait éliminer une partie de la non-linéarité de la relation température-millitension du thermocouple, de sorte que la sortie finale de l'appareil serait plus précise.

Le terme d'instrumentation populaire pour une telle table de consultation est un caractère numérique .

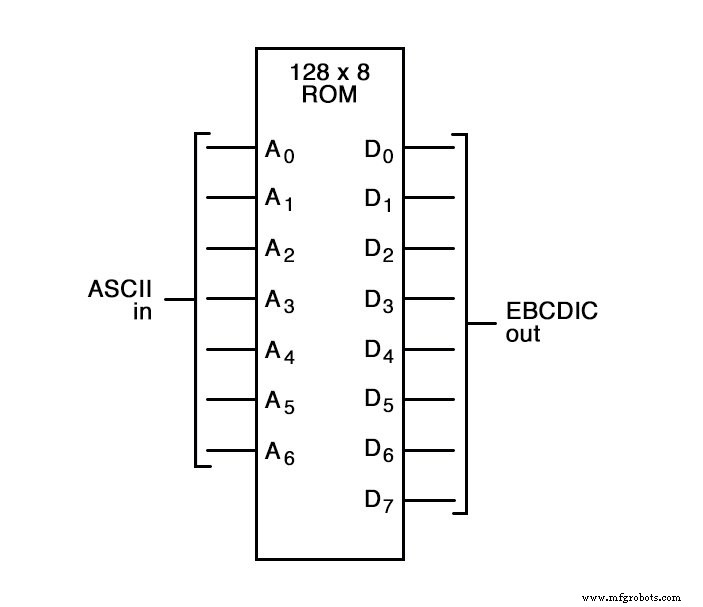
Une autre application pour les tables de consultation est la traduction de code spécial. Une ROM 128 x 8, par exemple, pourrait être utilisée pour traduire le code ASCII 7 bits en code EBCDIC 8 bits :

Encore une fois, tout ce qui est nécessaire est que la puce ROM soit correctement programmée avec les données nécessaires afin que chaque entrée ASCII valide produise un code de sortie EBCDIC correspondant.

FEUILLE DE TRAVAIL CONNEXE :

• Fiche de travail sur les périphériques de mémoire