Nombres binaires négatifs

L'addition étant facilement réalisable, nous pouvons effectuer l'opération de soustraction avec la même technique simplement en rendant l'un des nombres négatif. Par exemple, le problème de soustraction de 7 - 5 est essentiellement le même que le problème d'addition 7 + (-5).

Puisque nous savons déjà comment représenter les nombres positifs en binaire, tout ce que nous devons savoir maintenant est comment représenter leurs homologues négatifs et nous pourrons soustraire.

Habituellement, nous représentons un nombre décimal négatif en plaçant un signe moins directement à gauche du chiffre le plus significatif, comme dans l'exemple ci-dessus, avec -5. Cependant, tout le but de l'utilisation de la notation binaire est de construire des circuits marche/arrêt qui peuvent représenter des valeurs de bits en termes de tension (2 valeurs alternatives :soit « haute » ou « bas »).

Dans ce contexte, on ne s'offre pas le luxe d'un troisième symbole tel qu'un signe « moins », puisque ces circuits ne peuvent être que allumés ou éteints (deux états possibles). Une solution est de réserver un bit (circuit) qui ne fait que représenter le signe mathématique :

Comme vous pouvez le voir, nous devons être prudents lorsque nous commençons à utiliser des bits à d'autres fins que les valeurs pondérées par emplacement standard. Sinon, 1101₂ pourrait être mal interprété comme le nombre treize alors qu'en fait nous voulons représenter moins cinq.

Pour garder les choses au clair ici, nous devons d'abord décider combien de bits seront nécessaires pour représenter les plus grands nombres que nous traiterons, puis nous assurer de ne pas dépasser cette longueur de champ de bits dans nos opérations arithmétiques.

Pour l'exemple ci-dessus, je me suis limité à la représentation des nombres de moins sept (1111₂ ) à sept positif (0111₂ ), et pas plus, en faisant du quatrième bit le bit « signe ». Ce n'est qu'en établissant d'abord ces limites que je peux éviter la confusion d'un nombre négatif avec un nombre positif plus grand.

Représenter moins cinq comme 1101₂ est un exemple du système signe-grandeur de la numération binaire négative. En utilisant le bit le plus à gauche comme indicateur de signe et non comme valeur pondérée, je sacrifie la forme « pure » ​​de la notation binaire pour quelque chose qui me donne un avantage pratique :la représentation de nombres négatifs.

Le bit le plus à gauche est lu comme le signe, positif ou négatif, et les bits restants sont interprétés selon la notation binaire standard :de gauche à droite, placez les poids par multiples de deux.

Complémentation

Aussi simple que soit l'approche signe-grandeur, elle n'est pas très pratique à des fins arithmétiques. Par exemple, comment ajouter un cinq moins (1101₂ ) à tout autre nombre, en utilisant la technique standard d'addition binaire ?

Je devrais inventer une nouvelle façon de faire l'addition pour que cela fonctionne, et si je fais ça, je pourrais aussi bien faire le travail avec la soustraction longue; il n'y a aucun avantage arithmétique à utiliser des nombres négatifs pour effectuer une soustraction par addition si nous devons le faire avec une numération signe-grandeur, et c'était notre objectif !

Il existe une autre méthode pour représenter des nombres négatifs qui fonctionne avec notre technique familière d'addition à la main, et se trouve également avoir plus de sens du point de vue de la numération pondérée, appelée complémentation.

Avec cette stratégie, nous attribuons le bit le plus à gauche à un objectif particulier, tout comme nous l'avons fait avec l'approche signe-amplitude, définissant nos limites de nombre comme auparavant. Cependant, cette fois, le bit le plus à gauche est plus qu'un simple bit de signe; il possède plutôt une valeur de pondération de position négative. Par exemple, une valeur de moins cinq serait représentée comme telle :

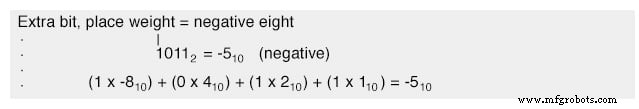
Avec les trois bits de droite pouvant représenter une grandeur de zéro à sept, et le bit le plus à gauche représentant zéro ou moins huit, nous pouvons représenter avec succès n'importe quel nombre entier de moins sept (1001₂ =-8₁₀ + 1₂ =-7₁₀ ) à sept positif (0111₂ =0₁₀ + 7₁₀ =7₁₀ ).

La représentation des nombres positifs dans ce schéma (avec le quatrième bit désigné comme le poids négatif) n'est pas différente de celle de la notation binaire ordinaire. Cependant, représenter des nombres négatifs n'est pas aussi simple :

Notez que les nombres binaires négatifs dans la colonne de droite, étant la somme du total des trois bits de droite plus les huit moins du bit le plus à gauche, ne « comptent » pas dans la même progression que les nombres binaires positifs dans la colonne de gauche.

Au lieu de cela, les trois bits de droite doivent être réglés sur la valeur appropriée pour égaler le total (négatif) souhaité lorsqu'ils sont additionnés avec la valeur négative à huit positions du bit le plus à gauche.

Complément à deux

Ces trois bits de droite sont appelés complément à deux du nombre positif correspondant. Considérez la comparaison suivante :

Dans ce cas, le bit de poids négatif étant le quatrième bit (valeur de position de moins huit), le complément à deux pour tout nombre positif sera la valeur qu'il faut ajouter à moins huit pour faire de cette valeur positive l'équivalent négatif.

Heureusement, il existe un moyen simple de déterminer le complément à deux pour n'importe quel nombre binaire :il suffit d'inverser tous les bits de ce nombre, en changeant tous les 1 en 0 et vice versa (pour arriver à ce qu'on appelle le complément à un), puis en ajouter un ! Par exemple, pour obtenir le complément à deux de cinq (101₂ ), on inverserait d'abord tous les bits pour obtenir 010₂ (le "complément à un"), puis en ajouter un pour obtenir 011₂ , ou -5₁₀ sous forme de complément à trois bits

Chose intéressante, la génération du complément à deux d'un nombre binaire fonctionne de la même manière si vous manipulez tous les bits, y compris le bit le plus à gauche (signe) en même temps que les bits de magnitude. Essayons cela avec le premier exemple, en convertissant un cinq positif en un cinq moins, mais en effectuant le processus de complémentation sur les quatre bits.

Nous devons être sûrs d'inclure le bit de signe 0 (positif) sur le nombre d'origine, cinq (0101₂ ). Tout d'abord, en inversant tous les bits pour obtenir le complément à un :1010₂ . Puis, en ajoutant un, on obtient la réponse finale :1011₂ , ou -5₁₀ exprimé sous forme de complément à deux à quatre bits.

Il est extrêmement important de se rappeler que la place du bit de poids négatif doit déjà être déterminée avant que des conversions de complément à deux puissent être effectuées. Si notre champ de numération binaire était tel que le huitième bit était désigné comme le bit de poids négatif (10000000₂ ), nous devrions déterminer le complément à deux sur la base des sept autres bits.

Ici, le complément à deux de cinq (0000101₂ ) serait 1111011₂ . Un cinq positif dans ce système serait représenté par 00000101₂ , et moins cinq comme 11111011₂ .

FICHES DE TRAVAIL CONNEXES :

• Feuille d'exercices de mathématiques binaires

Addition binaire Soustraction binaire