Demi-métallicité sans métal dans les systèmes gh-C3N4 dopés au B

Contexte

Les dispositifs spintroniques utilisent simultanément la liberté de charge et de spin des électrons et ont attiré de plus en plus d'attention en raison de leur utilisation potentielle dans les dispositifs logiques et de mémoire [1, 2]. Leurs performances dépendent cependant fortement du rapport de polarisation de spin des courants. Il existe donc un besoin pressant de matériaux capables de générer des courants polarisés en spin à 100 %. Des matériaux semi-métalliques, qui peuvent le faire au niveau Fermi E _F , sont considérés comme les matériaux idéaux pour les dispositifs spintroniques [3,4,5,6]. De nombreux ferroaimants semi-métalliques, tels que les manganites dopés [7], les doubles pérovskites [8] et les composés de Heusler [9, 10], ont attiré beaucoup d'attention ces dernières années. Cependant, ces matériaux semi-métalliques contiennent généralement un métal de transition (TM) et ont de fortes forces de couplage spin-orbite, ce qui entraîne des temps de relaxation de spin courts. Il est donc nécessaire de développer des matériaux semi-métalliques avancés sans TM avec un long temps de relaxation de spin.

Les cristaux atomiques bidimensionnels (2D) avec des surfaces planes ont récemment attiré beaucoup d'attention en raison de leur application potentielle dans les dispositifs spintroniques [11,12,13,14,15,16,17,18,19,20,21,22 ,23,24]. Le graphène et ses plusieurs analogues 2D, tels que le nitrure de bore hexagonal et le nitrure de carbone, ont un grand potentiel pour la spintronique en raison de leurs propriétés exceptionnelles, par exemple, la faible dimensionnalité et le confinement des électrons. Bien que la plupart de ces matériaux soient de nature non magnétique, il existe de nombreuses façons, telles que le dopage et la déformation, d'atteindre le ferromagnétisme semi-métallique. Par exemple, G-C₃ à base de trizaine intégré B, Al et Cu N₄ (gt-C₃ N₄ ) ont été rapportés comme étant semi-métalliques [14]. Le nitrure de carbone de type graphène présente également une demi-métallicité sous contrainte de traction [17]. De plus, le g-C₃ à base d'heptazine N₄ (gh-C₃ N₄ ) a reçu beaucoup d'attentions [25,26,27,28,29,30,31,32,33].

Un grand nombre de travaux de recherche ont étudié les propriétés électroniques et magnétiques du métal de transition incorporé gh-C₃ N₄ systèmes [11, 28, 30]. Ces métaux de transition incrustés de gh-C₃ N₄ matériaux ont été synthétisés à température élevée [34,35,36,37,38,39]. Des travaux théoriques montrent que les métaux de transition peuvent se lier plus fortement avec gh-C₃ N₄ qu'avec le graphène et ces systèmes sont métalliques [30]. Indrani et al. ont systématiquement étudié les propriétés magnétiques du C-dope gh-C₃ N₄ systèmes par calculs de la théorie de la fonctionnelle de la densité (DFT) [40]. Ils ont découvert que tous ces C-dope gh-C₃ N₄ sont le ferromagnétisme, et une phase à haute énergie montre une forte demi-métallicité et une température de Curie de 400 K. Récemment, Gao et al. [41] ont démontré expérimentalement la capacité de fabriquer le gh-C₃ dopé B N₄ nanofeuillets, qui présentent un ferromagnétisme à haute température et une demi-métallicité. Malgré ces premiers travaux, une étude théorique systématique du gh-C₃ dopé B N₄ est manquant. Quelques problèmes fondamentaux tels que les effets de la position de dopage et de la concentration en B sur les propriétés électroniques et magnétiques du gh-C₃ N₄ attendre des éclaircissements. De plus, les effets de la contrainte doivent également être étudiés.

Dans ce travail, nous étudions systématiquement les effets des positions de dopage, des concentrations de B et de la contrainte sur les propriétés électroniques et magnétiques du gh-C₃ dopé B. N₄ système par des calculs de principes premiers. Les résultats montrent qu'une forte demi-métallicité peut être trouvée dans l'état fondamental du gh-C dopé B₃ N₄ (B_C1 @gh-C₃ N₄ ). Non seulement les positions de dopage, mais aussi les concentrations de dopage jouent un rôle important dans l'induction de la demi-métallicité. De plus, la demi-métallicité dans B_C1 @gh-C₃ N₄ peut supporter jusqu'à 5 % de déformation en compression et 1,5 % de déformation en traction. Le gh-C₃ dopé B N₄ les systèmes sont donc prometteurs pour la spintronique.

Méthodes de calcul

Un tétragonal 28 a.u. cellule contenant deux cellules primitives de gh-C₃ N₄ comme le montre la figure 1 a été utilisé pour simuler le gh-C₃ dopé B N₄ système. La relaxation de la structure géométrique et le calcul de la structure électronique statique sont effectués en utilisant le package VASP [42, 43], qui est basé sur la théorie de la fonctionnelle de la densité (DFT). L'approximation à gradient généralisé (GGA) des potentiels de Perdew–Burke–Ernzerhof (PBE) [44] et d'onde augmentée par projecteur (PAW) est utilisée. L'énergie de coupure est fixée à 500 eV et une grille de points k de 1 × 9 × 15 Monkhorst-Pack est choisie pour atteindre un équilibre entre le temps de calcul et la précision. Toutes les structures géométriques sont complètement relâchées. Le seuil de convergence est fixé à 10 ⁻⁶ eV en pas électroniques et 5 × 10 ⁻³ eV/Å en vigueur. Afin d'éviter l'interaction entre deux images périodiques adjacentes, la région du vide le long du x -la direction est fixée à 15 Å. Pour étudier les effets des concentrations de dopage, une supercellule tétragonale de 112 atomes composée de 2 × 2 × 1 cellules unitaires tétragonales et une grille de points k de Monkhorst-Pack de 1 × 5 × 9 sont adoptées.

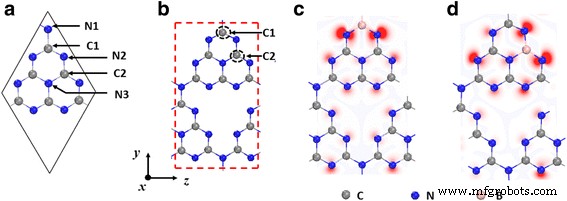
un Représentation schématique du gh-C₃ vierge N₄ . Il y a deux atomes C inéquivalents (C1 et C2) et trois atomes N inéquivalents (N1, N2 et N3). b Le tétragonal 28 a.u. cellule de gh-C₃ N₄ est utilisé ici pour simuler le gh-C₃ dopé B N₄ système (correspondant à une concentration de dopage de 8,33%). Les cercles en pointillés noirs indiquent les sites de dopage B possibles. c , d Les structures optimisées de B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ , respectivement. Distributions de densité de charge de l'état de démarrage moins l'état de ralentissement pour B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ sont également montrés ici. Les couleurs rouge et bleu indiquent respectivement les frais de démarrage et de ralentissement

Résultats et discussions

Dans un pur gh-C₃ N₄ système, il y a deux atomes C inéquivalents (C1 et C2) et trois atomes N inéquivalents (N1, N2 et N3) comme le montre la Fig. 1a. On retrouve les paramètres de maille relaxés (a = b = 7.14 Å) du gh-C₃ pur N₄ en accord avec les rapports expérimentaux et théoriques précédents [40, 45]. La structure de bande et la densité totale d'états (DOS) correspondante de gh-C₃ N₄ sont illustrés à la Fig. 2a. Pour mieux comprendre les propriétés électroniques du gh-C₃ N₄ , les distributions de charges des bandes de bord C ₁ , V ₁ , et la densité locale d'états correspondante sont présentés dans la Fig. 2b, c. On peut clairement voir que le bas de la bande de conduction C ₁ est dominé par le π ^* états des atomes C1, C2 et N3, qui proviennent du p _x orbitales. Cependant, le haut de la bande de valence V ₁ est déterminé par les états non liants des atomes N2 et les états des atomes N3.

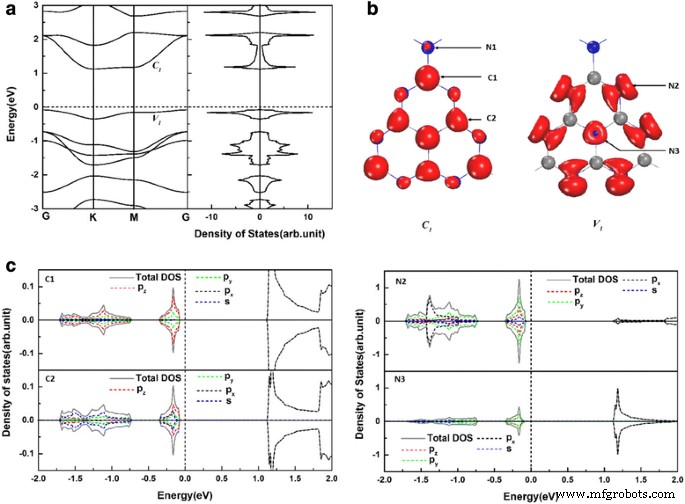
un Les structures de bandes électroniques et la densité totale d'états du gh-C₃ vierge N₄ . b Les distributions de charges des bandes de bord C ₁ et V ₁ (indexé dans a ). c La densité électronique résolue en orbite des états projetés sur l'atome C1, l'atome C2, l'atome N2 et l'atome N3 (indexé dans b ). L'énergie au niveau de Fermi est mise à zéro

Une maille tétragonale contenant 28 atomes de gh-C₃ N₄ (correspondant à une concentration de dopage de 8,333%) est utilisé pour simuler le gh-C₃ dopé B N₄ système comme le montre la Fig. 1b (la ligne pointillée rouge). Après avoir considéré les premiers rapports [31] selon lesquels la substitution sur les sites C (C1 et C2) est plus favorable que sur les sites N (N1, N2 et N3), seules les configurations de B substituant C ont été étudiées pour explorer leurs propriétés magnétiques. Propriétés. En conséquence, les deux différents gh-C₃ dopés B N₄ isomères (B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ ) sont étudiés. Les structures totalement relaxées de B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ sont donnés dans les Fig. 1c, d, respectivement.

La stabilité structurelle dépend de l'étendue de la cohésion et le système avec une énergie cohésive absolue négative et élevée a une meilleure stabilité. Les énergies de cohésion (E _coh ) de B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ ont été calculés en utilisant

où E _tot est l'énergie totale d'un gh-C₃ dopé B N₄ système et E _i est l'énergie d'un atome isolé pour l'élément i dans la même cellule. Le M _i et M sont le numéro du i e espèce et le nombre total d'atomes présentés dans le gh-C₃ dopé B N₄ système, respectivement. Nous trouvons que les énergies de cohésion sont de − 6.107 et − 6.097 eV par atome pour B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ , respectivement. Ainsi, le B_C1 @gh-C₃ N₄ phase est énergétiquement favorable. Cette conclusion est en bon accord avec les travaux antérieurs [31]. Pour approfondir l'étude de la stabilité relative des deux gh-C₃ dopés B N₄ systèmes, les énergies de cohésion de 2D C₂ N et gh-C₃ N₄ , qui ont été synthétisés expérimentalement, sont calculés et égaux à - 6.813 et - 6.091 eV par atome, respectivement. Fait intéressant, les deux B_C1 @gh-C₃ N₄ et B_C2 @ gh-C₃ N₄ ont des énergies de cohésion intermédiaires entre C₂ N et gh-C₃ N₄ . Par conséquent, ils doivent avoir une stabilité structurelle et mécanique intermédiaire.

Afin de déterminer la faisabilité thermodynamique et le coût énergétique relatif de B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ par rapport à leurs analogues 2D vierges, les énergies de formation ont également été calculées en utilisant

où E _tot , M _i , et M sont les mêmes que ceux pour le calcul de l'énergie de cohésion. μ _i est le potentiel chimique du i ème espèce. Ici, le graphène, le bore rhomboédrique et l'azote gazeux sont utilisés pour déterminer les potentiels chimiques μ _C , μ _B , et μ _N , respectivement. Les énergies de formation calculées sont de 0,222 et 0,232 eV par atome pour B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ , respectivement. A titre de comparaison, l'énergie de formation de gh-C₃ N₄ est de 0,293 eV par atome. De plus, le E calculé _f valeurs de B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ sont légèrement inférieurs à gh-C₃ N₄ , indiquant ces gh-C₃ dopé B N₄ les isomères peuvent être fabriqués. En effet, la synthèse de gh-C₃ dopé B N₄ a été signalé [41].

Afin de connaître les états fondamentaux magnétiques de B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ , nous avons étudié les états polarisés sans spin (NSP), ferromagnétique (FM) et antiferromagnétique (AFM). Les résultats montrent que l'état FM est l'état fondamental pour les deux gh-C₃ dopés B N₄ systèmes, et leurs moments magnétiques sont tous les deux de 1,0 μ _B par cellule unitaire comme indiqué dans le tableau 1. Pour mieux comprendre le magnétisme des deux gh-C₃ dopé B N₄ systèmes, les densités de charge dépendantes du spin de B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ ont été étudiés et représentés sur les Fig. 1c, d, respectivement. Légèrement différent du gh-C₃ dopé C N₄ systèmes dans lesquels la densité de spin est principalement localisée aux sites C dopés [40], la densité de spin de gh-C dopé B₃ N₄ est principalement localisé au niveau des atomes N2 coordonnés par 2, en particulier les atomes N2 adjacents aux atomes dopants B, comme le montrent les Fig. 1c, d. Parce que le dopant B a un électron de moins que l'atome C substitué, un défaut est induit dans le gh-C₃ dopé B N₄ système, résultant en 1.0 μ _B moment magnétique.

Pour comprendre les effets du dopage B sur le gh-C₃ N₄ systèmes, nous avons effectué les calculs de structure de bande polarisée en spin et de densité d'états pour B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ , comme le montrent les Fig. 3a, d, respectivement. Les résultats montrent que l'asymétrie entre les densités de spin-up et de spin-down dans B_C1 @gh-C₃ N₄ et B_C2 @gh-C₃ N₄ induit un magnétisme évident. Fait intéressant, comme le montre la figure 3a, nous constatons que le B_C1 @gh-C₃ N₄ les systèmes ont une propriété semi-métallique car l'un des canaux de spin est métallique, tandis que l'autre est isolant. Les graphiques de la structure des bandes et de la densité totale des états montrent que la division du spin se produit près du niveau de Fermi et que deux bandes de spin-down traversent le niveau de Fermi, tandis que celles de spin-up ont une bande interdite de 1,23 eV. Ceci est principalement dû aux grands vides présents dans le gh-C₃ N₄ framework, qui conduisent à la localisation des états électroniques. La bande interdite dans le canal de spin-up de B_C1 @gh-C₃ N₄ est bien plus grand que les écarts (dans l'un des canaux de spin) des manganites dopés [7], des doubles pérovskites [8], des composés de Heusler [9, 10] et du nanoruban de graphène [46]. La résistance semi-métallique du B_C1 @gh-C₃ N₄ les systèmes peuvent être comparables au gh-C₃ dopé C N₄ [40]. Un système semi-métallique aussi fort est très prometteur car la transition spin-flip des porteurs à partir de l'excitation thermique n'est pas possible. Explorer davantage les origines de la demi-métallicité dans B_C1 @gh-C₃ N₄ , les distributions de charge des deux bandes de spin-down qui traversent le niveau de Fermi sont présentées dans la Fig. 3b. On voit bien que la demi-métallicité de B_C1 @gh-C₃ N₄ provient principalement des états non liants des atomes N2. La densité locale d'états (voir Fig. 3c) montre également que la demi-métallicité de B_C1 @gh-C₃ N₄ provient principalement du p _z orbites d'atomes N2 avec une contribution partielle du p _z orbites des atomes B et N1. Ils sont en bon accord avec les rapports précédents sur gt-C₄ N₃ [2], où les orbitales N apportent une contribution majeure à la demi-métallicité. Pour le B_C2 @gh-C₃ N₄ , les graphiques de la structure de bande et de la densité totale d'états (Fig. 3a) montrent également que la division du spin se produit près du niveau de Fermi. L'état majoritaire de spin a une bande interdite de 1,36 eV. Cependant, l'état minoritaire de spin montre une bande interdite de 0,016 eV. Les distributions de charge des bandes de bord et la densité locale d'états pour B_C2 @gh-C₃ N₄ montrer que les bords de la bande de valence et les bords de la bande de conduction de B_C2 @gh-C₃ N₄ sont dominés par les états non-liants, provenant principalement des p _y et p _z orbitales des atomes N2. Cela signifie que les états non-liants des atomes N2 sont divisés lorsqu'un atome B remplace un atome C dans gh-C₃ N₄ système et déterminer ses propriétés électroniques.

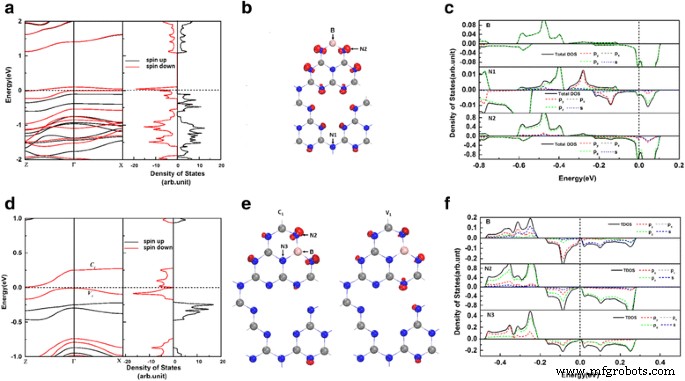
un La structure de bande dépendante du spin et la densité totale d'états de B_C1 @gh-C₃ N₄ . b Les densités de charges des deux bandes traversant le niveau de Fermi. c La densité électronique résolue en orbite des états projetés sur l'atome B, l'atome N1 et l'atome N2 (indexé dans b ) pour B_C1 @gh-C₃ N₄ . d –f sont les mêmes avec a –c mais pour B_C2 @gh-C₃ N₄ . L'énergie au niveau de Fermi est mise à zéro

Afin de clarifier la dépendance de la demi-métallicité dans le B_C1 @gh-C₃ N₄ systèmes sur les concentrations de dopage, une supercellule tétragonale à 112 atomes de 2 × 2 × 1 cellule unitaire tétragonale a été utilisée et trois concentrations différentes de dopage B (2,083, 4,167 et 6,25 %) sont étudiées, comme le montrent les Fig. 4a, b . Comme nous pouvons le voir sur la figure 4b, B_C1 @gh-C₃ N₄ peut encore supporter la demi-métallicité pour une concentration de dopage de 6,25 %. Cependant, il perd sa demi-métallicité car la concentration de dopage est égale ou inférieure à 4,167%.

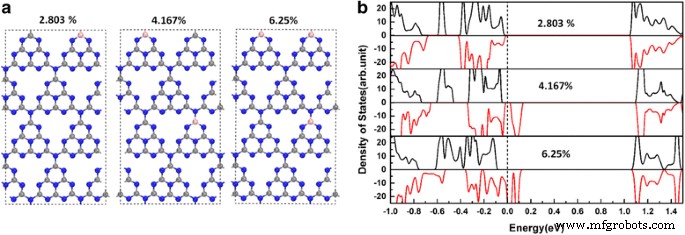
un Représentations schématiques de la supercellule tétragonale à 112 atomes utilisée pour simuler différentes concentrations de dopage de B_C1 @gh-C₃ N_4. b La densité totale d'états dépendante du spin de B_C1 @gh-C₃ N₄ avec différentes concentrations de dopage. L'énergie au niveau de Fermi est mise à zéro

La technologie de déformation est couramment utilisée pour régler les propriétés de spin d'un matériau magnétique, et l'effet de déformation sur la demi-métallicité d'un matériau doit être étudié. Ici, nous avons effectué les calculs de densité d'état pour le B_C1 @gh-C₃ N₄ système sous la déformation biaxiale en plaine. On constate que la résistance à la demi-métallicité diminue progressivement à mesure que la contrainte de traction biaxiale augmente. Il perd la demi-métallicité lorsque la déformation de traction biaxiale atteint 1,5%, comme indiqué dans le panneau de la Fig. 5. Cependant, il supporte la demi-métallicité jusqu'à 5% de la déformation de compression biaxiale (voir le panneau de droite de la Fig. 5). Ainsi, ce système se comporte bien sous contrainte externe.

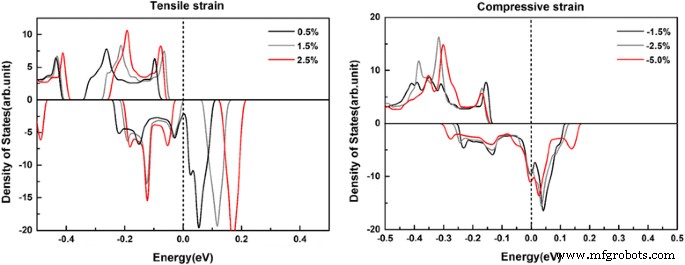
La densité totale d'états dépendante du spin de B_C1 @gh-C₃ N₄ (avec une concentration de dopage de 8,33 %) sous une contrainte de traction biaxiale en plaine (à gauche) et une contrainte de compression biaxiale (à droite), respectivement. L'énergie au niveau de Fermi est mise à zéro

Conclusion

Basé sur les calculs de la théorie fonctionnelle de la densité, le gh-C₃ dopé B N₄ systèmes ont été étudiés pour des applications potentielles dans les dispositifs spintroniques. Le ferromagnétisme est observé dans tous les gh-C₃ dopé B N₄ systèmes. De plus, une forte demi-métallicité n'est obtenue que dans la phase d'état fondamental, c'est-à-dire B_C1 @gh-C₃ N₄ , qui résulte d'une scission de spin des états δ non liés d'atomes N2 hautement insaturés coordonnés 2 fois. La demi-métallicité est perdue pour les faibles concentrations de dopage B. Ainsi, le dopage sélectif et sa concentration jouent un rôle important dans l'induction du magnétisme et de la demi-métallicité. La demi-métallicité en B_C1 @gh-C₃ N₄ peut supporter jusqu'à 5 % de déformation en compression et 1,5 % de déformation en traction. Ces résultats montrent que le gh-C₃ dopé B N₄ les systèmes pourraient être un matériau semi-métallique ferromagnétique pour la mémoire magnétique et les dispositifs spintroniques.